Обобщающие статистические показатели

1. Обобщающие показатели

1. Абсолютные показатели, их виды
2. Относительные показатели, их виды
3. Средние показатели, их виды

2.

Обобщающие статистические показатели –
отражают количественную сторону изучаемой
совокупности и служат базой анализа и
прогнозирования социально-экономического
развития отдельных предприятий, регионов и
страны в целом.
В зависимости от исследуемого признака
обобщающие показатели выражаются через
абсолютные, относительные и средние
величины.

3.

Выделяют:
- натуральные (шт, га, тонн, км и т.д.);
- условно-натуральные (усл. гол; условное
мыло, содержащее 40% жирных кислот )
- стоимостные (руб, коп) ;
- трудовые единицы измерения (чел-час, челдней).

4.

Виды абсолютных показателей:
По степени охвата исследуемой совокупности
:
• индивидуальные, характеризующие
отдельные единицы совокупности;
• общие, отражающие размеры признака в
совокупности в целом .

5.

• Моментные – показывают фактическое
наличие
или
уровень
явления
на
определенный момент, т.е. на дату;
• Интервальные – итоговый накопленный
материал за какой-либо период;

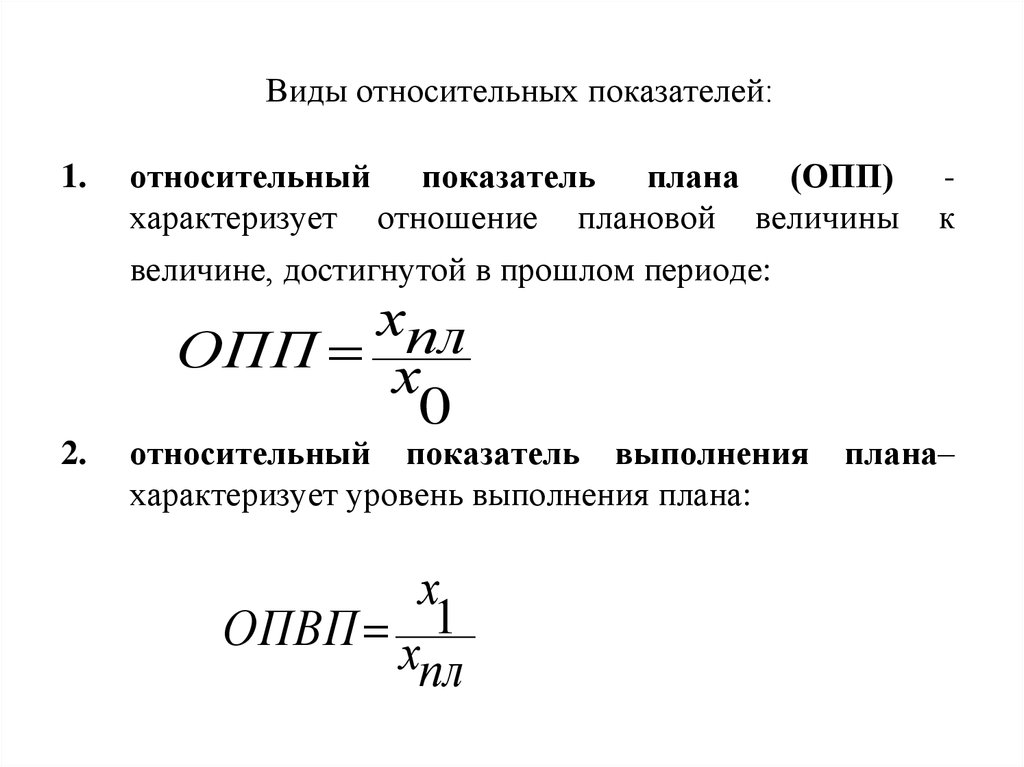
6. Виды относительных показателей:

1.
относительный показатель плана (ОПП)
характеризует отношение плановой величины
к
величине, достигнутой в прошлом периоде:
хпл
ОПП х
0
2.
относительный показатель выполнения
характеризует уровень выполнения плана:
х
ОПВП х 1
пл
плана–

7.

3. Относительный показатель динамики – характеризует
изменение изучаемого явления во времени, выявляет
направление развития и измеряет интенсивность развития
явления:
х
ОПД х1
0
Произведение относительного показателя плана на
относительный показатель выполнения плана дает
относительный показатель динамики:
ОПП*ОПВП ОПД

8. Таблица 1 – Оборот фирмы

Показатель
2014 г
x
0
2015 г
По плану
x
Оборот,
млн. руб.
20
пл
28
Фактически
x
1
26

9.

4. Относительный показатель структуры – характеризует
состав изучаемых совокупностей:
х
ОПС i
х
5. Относительный показатель сравнения – характеризует
количественное соотношение одноименных показателей,
относящихся к различным объектам статистического
наблюдения:
величина
_
обьекта
_
А
ОПСр
величина_ обьекта_ Б

10.

6.
Относительный
показатель
координации
–
характеризует соотношение между отдельными частями
одной статистической совокупности:
одна
_
часть
_
целого
ОПК
другая_часть_целого
7.
Относительный показатель интенсивности –
характеризует степень распространения изучаемого
явления в присущей ему среде:
ОПИ
размер_ явления
среда_ распространения _ этого_ явления

11. Виды средних величин:

1. Средняя арифметическая простая:
x x x ... xn
х
х
1 2 3
n
n
Средняя арифметическая взвешенная:
xf x1 f1 x 2 f 2 x3 f 3 ... xn f n
х
f f f ... f n
f
1 2 3

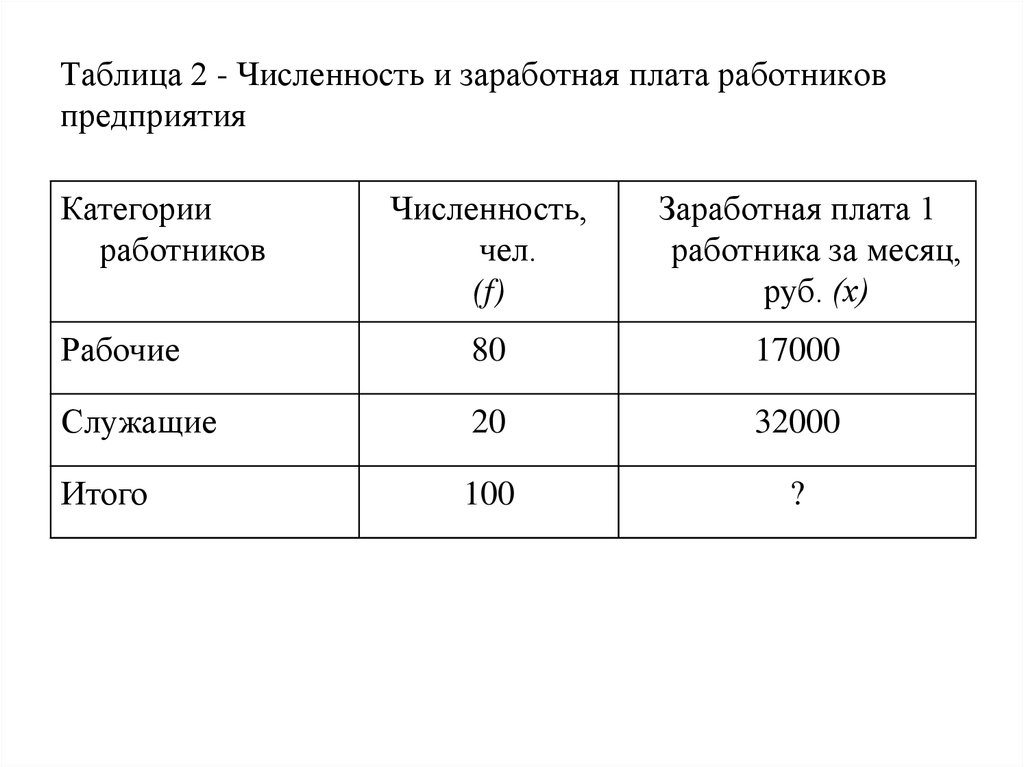
12. Таблица 2 - Численность и заработная плата работников предприятия

Категории
работников
Численность,
чел.
(f)
Заработная плата 1
работника за месяц,
руб. (х)
Рабочие
80
17000
Служащие
20
32000
Итого
100
?

13. Математические свойства средней арифметической:

1.
Произведение средней на сумму частот равно сумме
произведений отдельных вариантов на соответствующие
им частоты:
х f x * f
2.
Сумма отклонений индивидуальных значений признака
от средней арифметической равна нулю:
( x x) 0
3.
( x x) * f
0
Сумма квадратов отклонений индивидуальных значений
признака от средней арифметической меньше, чем сумма
квадратов отклонений от любой другой произвольной
величины А:
( х х) ( х А)
2
2

14.

4. От уменьшения или увеличения частот каждого значения
признака х в А раз величина средней арифметической не
изменится:
f
х* А
х
f
А
5. Если от каждого варианта вычесть или к каждому
варианту прибавить какое-либо постоянное число А, то
средняя уменьшается или увеличивается на то же самое
число А:
( х А) * f x А
f

15.

6. Если все варианты значений признака уменьшить или
увеличить в А раз, то средняя также соответственно
увеличится или уменьшится в А раз:
х
А* f
x
А
f
7. Общий множитель индивидуальных значений признака
может быть вынесен за знак средней:
А* x А* x
8. Средняя суммы (разности) двух или нескольких величин
равна сумме (разности) их средних:
x y x y

16.

2. Средняя гармоническая взвешенная:
W W W ... Wn
W
2
3
х
1
W W1 W2 W3 ... Wn
x
x
x
x
xn
1
2
3
Средняя гармоническая простая:
n
n
x
1
1
1
1
1
...
x
x
x
xn
x
1
2
3
i

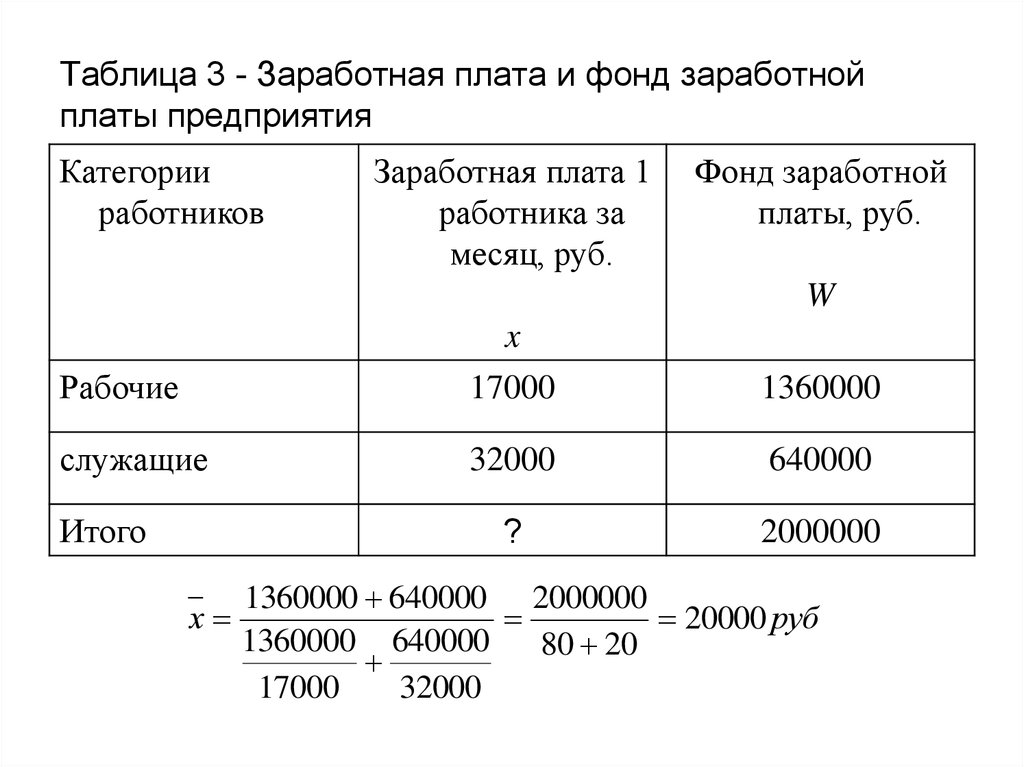
17. Таблица 3 - Заработная плата и фонд заработной платы предприятия

Категории
работников
Заработная плата 1
работника за
месяц, руб.
Фонд заработной
платы, руб.
W
x
Рабочие
17000
1360000
служащие
32000
640000
?
2000000
Итого
1360000 640000 2000000
х
20000 руб
1360000 640000
80 20
17000
32000

18.

3. Средняя хронологическая простая:
1/ 2x x x ... 1/ 2 xn
1 2 3
x
n 1
Средняя хронологическая взвешенная:
( x x )*t ( x x )*t ... ( x xn )*tn 1
n 1
x 1 2 1 2 3 2
2* t

19. Таблица 4 - Численность работников предприятия

Даты
Численность,
чел
1 января 1 апреля
2013 г
2013 г
500
550
1 июля 1 октября 1 января
2013 г
2013 г
2014 г
530
545
520
1
1
500 550 530 545 520
2
х 2
534чел
5 1

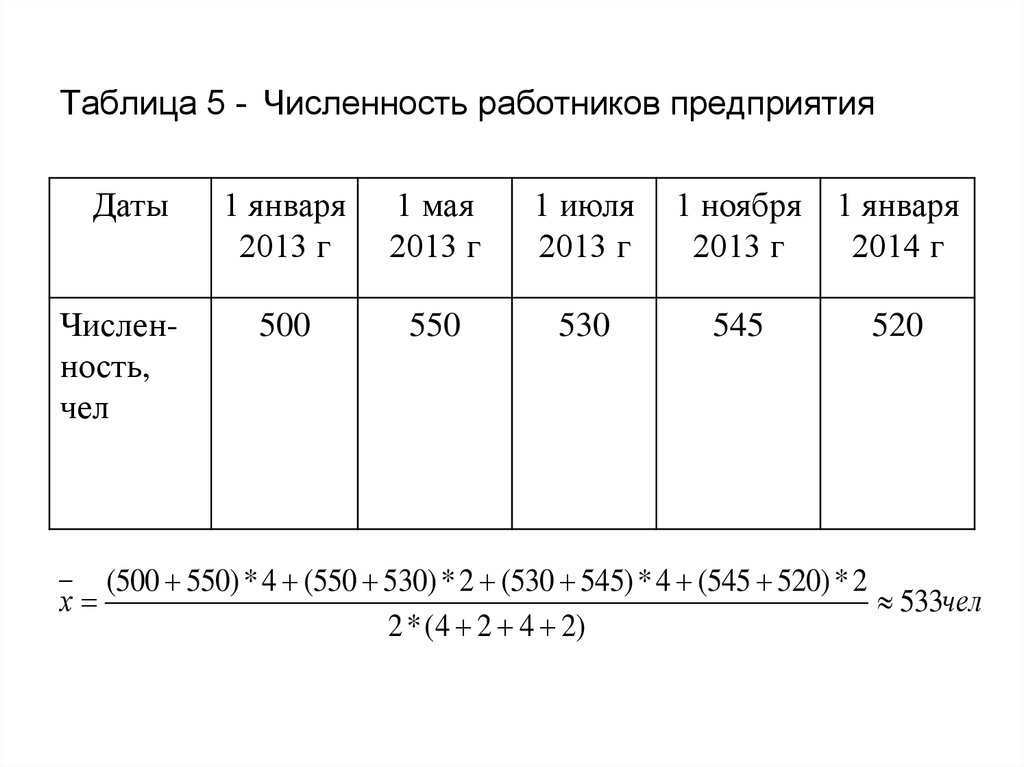
20. Таблица 5 - Численность работников предприятия

Даты
Численность,
чел
1 января
2013 г
1 мая
2013 г
1 июля
2013 г
500
550
530
1 ноября 1 января
2013 г
2014 г
545
520
(500 550) * 4 (550 530) * 2 (530 545) * 4 (545 520) * 2
х
533чел
2 * (4 2 4 2)

21.

4. Средняя геометрическая:
xn
x n 1
x
1
x m k * k * k *...* km
1 2 3
xi
k
x
i 1

22. Таблица 6 - Динамика производства продукции на предприятии

Годы
х
5 1
Производство
продукции, млн.
руб.
Цепные коэффициенты
роста
2009
120
-
2010
128
1,067
2011
119
0,930
2012
116
0,975
2013
125
1,078
125
1,010 *100 101%
120
х 4 1,067 * 0,930 * 0,975 *1,078 1,010 *100 101%

23.

5. Средняя квадратическая простая:
x
x x ... x
x
n
2
1
2
2
2
n
2
i
n
Средняя квадратическая взвешенная:
x
x
f
2
i
fi
i

24.

6. Средняя кубическая простая:
x 3
x
3
i
n
Средняя кубическая взвешенная:
x
3
x f
f
3
i
i
i

25. Структурные средние:

• Мода:
(f
f
)
Mo 1
Mo x h
0
(f
f
) ( f
f
)
Mo
Mo
Mo 1
Mo 1
Mo
• Медиана:
Ìå õ0 h
1
2
f
S Me 1
f Me

26. Распределение работников по стажу работы

Стаж, лет
Число работников, чел
Mo 6 2*
до 2
2-4
4-6
6-8
8-10
4
23
20
35
11
(35 20)
6,7года
(35 20) (35 11)
св.
10
7

27.

Распределение работников по стажу работы
Стаж, лет
св.
до 2
2-4
4-6
6-8
8-10
Число работников, чел (f)
4
23
20
35
11
7
Накопленные частоты, (S)
4
27
47
82
93
100
Ме 6 2
1
2
100 47
35
10
6,17 года