Похожие презентации:
Случайные величины. Дискретная случайная величина
1. Тема 2. Случайные величины
Дискретная случайная величина (д.с.в.)I.
§ 1. Определение. Числовая функция, заданная на пространстве
элементарных событий, называется случайной величиной.
Пример.
§ 2. Распределение дискретной случайной величины
xi=X(ωi ) pi= P{X=xi};
Опр. Соответствие, которое каждому значению xi д.с.в. Х сопоставляет его
вероятность pi называется законом распределения с.в. Х.
Х
P
х1
х2
p1
p2
…
…
хn
pn
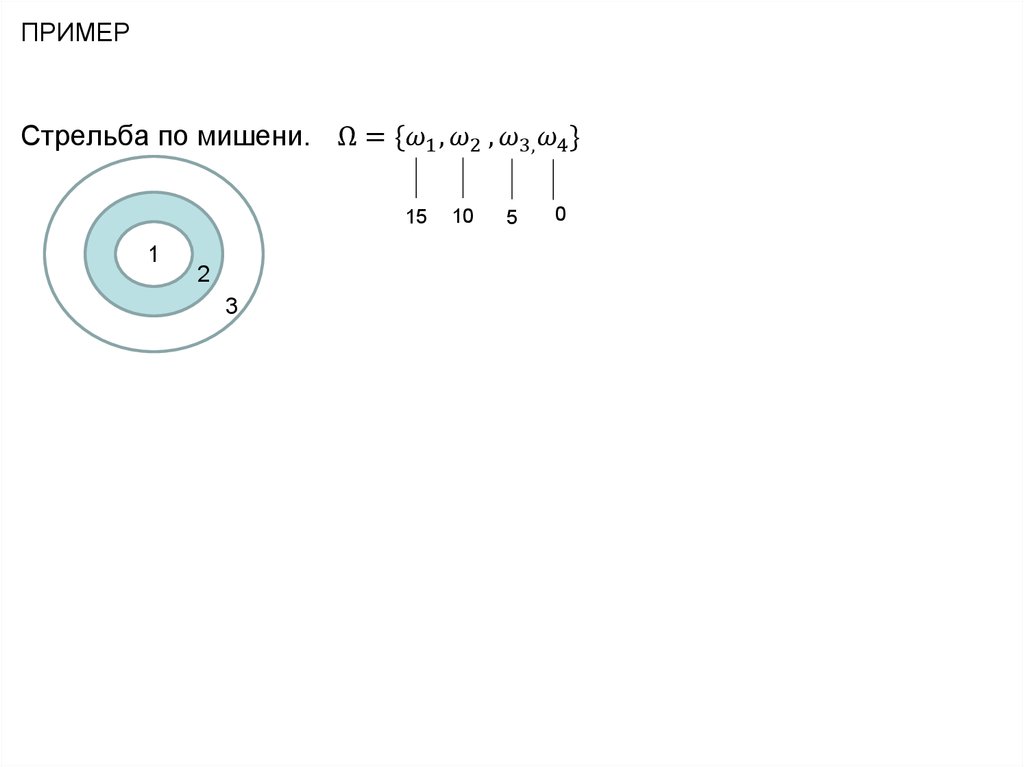
Пр.1 Стрельба по мишени.
Х
0
5
10
15
Р
0,1
0,4
0,3
0,2
n
pi 1
i 1
2. пример
ПРИМЕРСтрельба по мишени. Ω = {






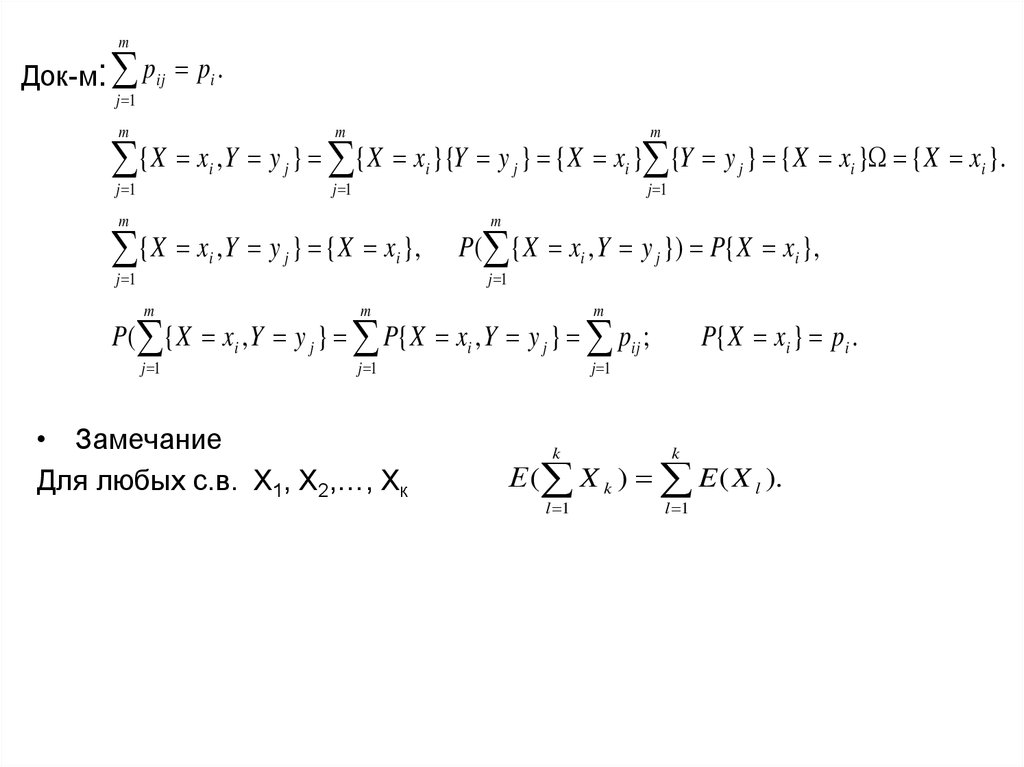







 Математика
Математика








