Похожие презентации:
fiz-3_Lektsia_mag
1.
2 ЭЛЕКТРОМАГНИТТІК ИНДУКЦИЯ2.1 Электромагниттік индукция құбылысы
Магнит өрісінің электр тогын тудыру құбылысын электромагниттік
индукция деп атаймыз.
Егер магнитті катушкаға жақындатсақ, өткізгіште
ток пайда болады. бұны индукциялық ток деп
атайды.
Фарадейдің қорытындысы:
1. индукциялық ток ылғи да контурды қиып өтетін
магнит ағыны өзгерген кезде болады;
2. индукция тогының мөлшері магнит индукциясы ағынын өзгерту тәсіліне
тәуелді болмайды, ол тек қана магнит ағынының өзгеру жылдамдығымен
анықталады.
1
2.
Фарадей заңының математикалық өрнегі:dФ
i
dt
(2.1.1)
Индукция электрқозғаушы күші магнит ағынының өзгеру жылдамдығына тең
болады. Минус таңбасын Ленц ережесі арқылы түсіндіруге болады.
Ленц ережесі: контурдағы индукциялық ток бағыты ылғи да оны туғызған
магнит ағынының өзгеруіне қарама-қарсы бағытта болады.
dФ
dФ
0
0 болады, яғни
i
Егер ағын өсетін
болса, онда
dt
dt
пайда болған индукциялық ток ағынға қарсы бағытталған өріс туғызады.
Фарадей заңы индукция ЭҚК-нің шамасын, ал Ленц ережесі бағытын
анықтайды.
N орам контур үшін индукцияланған ЭҚК-і былай болады:
dФ
i N
dt
(2.1.2)
2
3.
2.2 Өздік индукция құбылысыТұйық контурда ток күшінің өзгеруі осы контурды қиып өтіп жатқан магнит
өрісінің ағынын өзгертеді, ал магнит ағынының өзгерісі өз кезегінде осы
контурда индукциялық ЭҚК-ін тудырады. Бұл құбылыс - өздік индукция
құбылысы деп аталады.
Контурдың ауданын қиып өтетін магнит ағыны (Ф=BS) контурдағы токқа
тура пропорционал болады:
Ф LI .
(2.2.1)
Пропорционалдық коэффициенті L=Ф /I
контурдың индуктивтілігі деп аталады. Ол
сан мәні жағынан ток күші бірлігіндегі магнит ағынын сипаттайды.
Индуктивтілік өлшемі бірлігі генри (Гн) . Контурдағы ток күші 1А болғанда,
магнит ағыны 1 вебер болса, онда контурдың индуктивтілігі 1 Гн-ге тең
болады.
Өздік индукция ЭҚК-ін жалпы индукция заңын пайдаланып табуға болады:
dФ
d
dL
dI
S
( LI ) L I
dt
dt
dt
dt
(2.2.2)
3
4.
Егер L = const болса, ондаs L
dI
dt
(2.2.3)
Бұл формуладағы минус таңбасы Ленц ережесінен шығады, ток өскенде
өздік индукция ЭҚК-і ε < 0 немесе өздік индукция тогы сыртқы ток
көзінен пайда болған токқа қарсы бағытталған, сондықтанда оның өсуіне
кедергі жасайды. Егер ток азаятын болса, онда өздік индукция ЭҚК-і ε > 0
болады да, контурдағы азаюшы ток пен өздік индукция тогының бағыттары
бірдей болып, токтың азаюы баяулайды.
Жалпы орам саны N, орам қимасы S, ұзындығы ℓ болатын соленоидтың
индуктивтілігін есептейік. Соленоидтың ішінде индукциясы В-ға тең магнит
өрісі қозады:
B 0
Әрбір орам арқылы ағын Ф=BS болады, ал
толық ағын
NI
0 nI
n N
мұндағы n – бірлік
ұзындықтағы орам саны.
NФ n BS 0 n 2 SI
(2.2.4)
L 0 n 2 S 0 n 2V
(2.2.5)
V S
соленоидтың көлемі.
4
5.
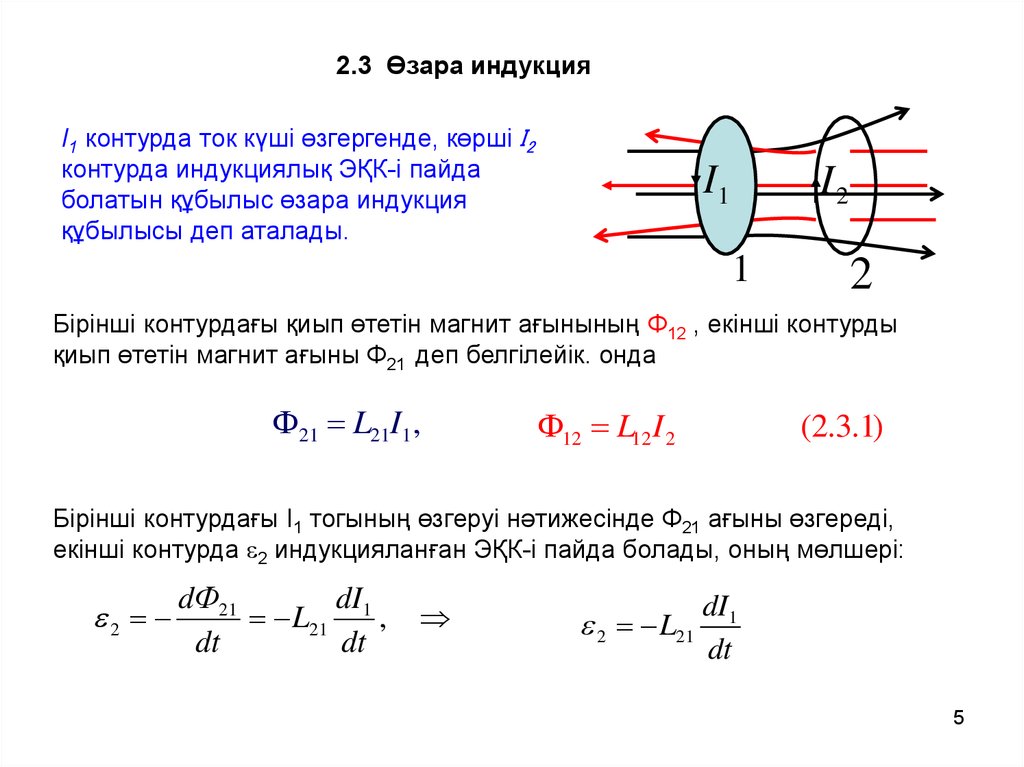
2.3 Өзара индукцияI1 контурда ток күші өзгергенде, көрші I2
контурда индукциялық ЭҚК-і пайда
болатын құбылыс өзара индукция
құбылысы деп аталады.
I1
I2
1
2
Бірінші контурдағы қиып өтетін магнит ағынының Ф12 , екінші контурды
қиып өтетін магнит ағыны Ф21 деп белгілейік. онда
21 L21I1 ,
12 L12 I 2
(2.3.1)
Бірінші контурдағы І1 тогының өзгеруі нәтижесінде Ф21 ағыны өзгереді,
екінші контурда 2 индукцияланған ЭҚК-і пайда болады, оның мөлшері:
dФ21
dI1
2
L21
,
dt
dt
2 L21
dI1
dt
5
6.
Енді екінші контурда ток өзгеріп, ал бірінші контурда индукцияланған токпайда болатын жағдайды қарастырайық. Онда:
1 L12
dI 2
dt
мұндағы І2 – екінші контурдағы ток күші; 1 – бірінші контурда пайда
болған ЭҚК-і. Пропорционалдық коэффициенттер L12 және L21
контурлардың өзара индуктивтілігі деп аталады. Ферромагнетиктер
болмаған жағдайда бұл коэффициенттер бір-біріне тең болады: L12=L21.
d 12
d I2
1
L12
,
dt
dt
2
d 21
dI
L21 1 .
dt
dt
(2.3.2)
L12 және L21 коэффициенттерінің шамасы контурлардың геометриялық
формасы мен мөлшерімен, контурлардың бір-біріне байланысты
орналасуымен және де контурларды қоршаған ортаның магнит
өтімділігімен анықталады.
6
7.
2.4 Магнит өрісінің энергиясы және оның көлемдіктығыздығы
Бойымен І тогы жүретін контурды қарастырайық. Контурдың индуктивтілігі L
болсын. Егер контурдағы ток dІ-ге өзгерсе, онда онымен ілініскен ағын
dФ=LdІ-ге өзгереді, ал мұнда істелінген жұмыс dА= dФ=L dІ болады. Ф
ағыны пайда болуға қажетті жұмысI
A LIdI LI 2 / 2
(2.4.1)
0
.
тең болады. Контурмен байланысқан магнит
өрісінің энергиясы:
2
LI
(2.4.2)
W
.
2
Енді ұзын соленоидтың ішіндегі біртекті магнит өрісінің энергиясын есептейік.
L = 0n2V, B = 0Н, Н = nІ екені белгілі. L мен І-дің мәндерін
(2.4.2)-ге қоятын болсақ:
0 H 2
BH
B2
W
V
V
V,
(2.4.3)
мұндағы V = Sl – соленоид көлемі.2
2
2 0
Энергия соленоид ішіне топтасқан және тұрақты көлемдік тығыздықпен
W
V
таралған болады. Сонымен,
0 H 2
2
BH
B2
2
2 0
(2.4.4)
7
8. 2.5 Максвелл теңдеулері
Максвеллэлектр
және
магнит
өрістерінің
біріккен теориясын жасап тәжірибеден
алынған
құбылыстарды
түсіндіріп
электромагниттік толқындардың
бар екенін айтып жарықтың электромагниттік
теориясын жасады.
Максвелдің бірінші тендеуі
өрісінің көзі тек
Фm
B электр
E
d
d
S
(2.5.1)
қана зарядтар
ғана S емес
t
t
айнымалы магнит
өрісі де электр өрісінің көзі
Hнақтылайды.
Максвелдің
екінші теңдеуі
–
векторының
бола алатынын
циркуляциясы
туралы
теореманы
Оның математикалық
өрнегінің
түрі: жалпылау. Бұл
теңдеу магнит өрісін электр тогы (қозғалыстағы
Dэлектр
заряд) немесе айнымалы
өрісі (ығысу тогы)
ûãûñó
H
d
j
d
S
I
.
(2.5.2)
îò яғни
тудыратынын көрсетеді,
t
Максвеллдің үшінші теңдеуі
– Гаусс теоремасының жал
n
D
бұл теңдеу
D dS q ,
n
i 1
i
(2.5.3)
векторының сызықтары зарядтардан
аяқталатынын көрсетеді. Максвеллдің төртінші теңде
B
Бұл теңдеу
B dS 0.
n
(2.5.4)
векторының сызықтарының тұйық екен
зарядтарының жоқ екенің нақтылайды.
8
9. 3 Электромагниттік тербелістер
Электромагниттіктербелістер
3.1 Тербелмелі контур.
Актив кедергісі жоқ
контурдағымен
еркін
тербеліс
Индуктивтілігі
сыйымдылығы
бар тізбекте эл
Мұндай тізбек тербелмелі контур деп аталады. С
процестің идеалды актив кедергісіз контурдағы
Біртекті емес тізбек үшін Ом заңының өрнегін жаза
IR 1 2 12
.
(3.1.1)
Берілген жағдай үшін R=0, 1– 2=-q/C, 12= s=-L(dI/dt), бұл мәнде
қойып, алатынымыз:
0 = -q/C – L(dІ/dt),
(3.1.2)
бұдан
q
1
q 0
LC
өрнегін аламыз. Егер 1
0
LC
деп белгілеп алсақ, онда
q 02 q 0.
q=qmcos( t+ ).
Бұл теңдеудің шешімі:
(3.1.3)
(3.1.4)
(3.1.5)
(3.1.6)
9
10.
Тербелістің периоды Томпсон формуласынан аныT 2 LC
(3.1.7)
3.2 Еркін өшетін
тербелістер
Нақты контурда әрқашанда актив кедергі болады
біртіндеп осы кедергілерде шығындалады, соның е
q
dI
IR L
(3.2.1)
C
dt
R
1
q q
q 0
(3.2.2)
L
LC
2 = R/L
..
q 2 q 02 q 0
t
q
q
e
cos( t )
Бұл теңдеудің шешімі:
mo
(3.2.3)
(3.2.4)
Тербелістің өшуін өшудің логарифмдік декрементіме
q(t )
ln
T .
(3.2.5)
q(t T )
Мұндағы а(t) қандай да бір шаманың ам
(q, U немесе І).
Өшудің логарифмдік декременті амплитуда е есе а
тербеліс санына кері екенін ескерсек, онда / e.
қойып және Т-ның орнына 2 / ауыстырып, -ны табам
10
R/2L = R/L .
(3.2.6)
11.
Еріксіз электрЕріксіз 3.3
тербеліс
болуытербелістері
үшін, сырттан
системаға периодты түрде әсер ету керек. Ол
үшін
контурдың
элементтеріне
тізбектей
айнымалы ЭҚК немесе айнымалы
U =Um cos t
(3.3.1)
кернеу беру керек. Бұл кернеуді өздік
индукцияның ЭҚК-не қосамыз.
q
dI
Нәтижесінде Ом
IRзаңы
Lмына
U m cos t
(3.3.2)
C
dt
түрге келеді. Мұны түрлендіріп еріксіз электр тер
теңдеуін аламыз:
U
q 2 q 02 q m cos t
(3.3.3)
L
Бұл теңдеудің дербес
q = qшешімі:
(3.3.4)
m cos( t - ),
.
.
Um
R
мұндағы q
,
tg
.
(3.3.5)
m
2
2
1
R L 1 / C
L
C
q
dI
Енді (3.3.2) өрнегін мына түрде
IR жазайық:
L U cos t ,
бұдан
UR + UC + UL = U cos t .
C
dt
m
(3.3.6)
(3.3.7)
11
12.
UR = ІmR cos( t - ).(3.3.7) өрнекке сәйкес:
(3.3.8)
(3.3.4) өрнекті сыйымдылыққа бөліп, конденсатордағы к
qm
UC
cos t U cm cos( t / 2),
(3.3.9)
c
мұндағы
q
Um
I
U cm m
m .
(3.3.10)
2
C
C
1
c R 2 L
c
I I m cos( t )
Енді
теңдеуінің туындысын L-ге көбейті
кернеуді табамыз:
UL L
мұндағы
dI
LI sin t U Lm cos( t / 2),
dt
U Lm LI m
(3.3.11)
(3.3.12)
12
13.
Айнымалысыйымдылығы,электр тогы
Орныққан еріксіз3.4
тербелісті
индуктивтілігі және актив кедергісі
бар тізбектен айнымалы токтың өтуі деп
қарастыруға болады,
ол
U = Um cos t
(3.4.1)
айнымалы
кернеуден
пайда
болды
деп
ескереміз. Бұл ток:
І =Іm cos( t - )
(3.4.2)
заңы бойынша өзгереді. Ток амплитудасы Іm
кернеу амплитудасымен Um, C, L,
R, тізбек параметрлерімен
анықталады:
Um
Im
.
(3.4.3)
2
2
R ( L 1 / C )
Ток кернеуден фаза бойынша бұрышқа қалып
отырады, ол тізбектің
параметрлеріне және
байланысты:
Lжиілікке
1 ток
/ C
0
болған
жағдайда
кернеуден
озып
tg
.
(3.4.4)
R
отырады. (3.4.3) өрнектің бөлімі
толық
электр кедергісі
немесе
импеданс
аталады. Егер
Z R ( L 1 / Cдеп
)2
тізбекте тек актив кедергі ғана болса, онда Ом
заңы ІR = Um cos t түрін
қабылдайды.
Бұл
жерде
ток
кернеумен
бір
фазада болады, ток күшінің
амплитудасы Іm = Um / Z .
13
14.
.Кез-келген
нақты
тізбекте
R,C,L
болады.
Кейбір жеке жағдайларда бұл
параметрлердің кейбіреулерінің токқа әсерін
ескермеуге болады. Мысалы,
тізбектегі R-дің мәнін нөл деп, ал С мәнін
шексіздікке тең деп алуға болады.
Онда (3.4.3), (3.4.4) формуладан:
Іm = Um / L ,
(3.4.5)
ал tg = екені шығады.
ХL= L
(3.4.6)
ХL шамасын индуктивтік
кедергі деп
Индуктивтікте
ток кернеуден
/2 -ге қалып
атайды.
отырады. Енді R мен L-ді нөлге тең
деп алайық. Онда (3.4.3),(3.4.4) формулаларынан:
Іm=Um С,
(3.4.7)
tg =- аламыз.
XC =1/ C
(3.4.8)
шамасын сыйымдылық кедергі деп атайды.
Х= L - 1/ C
= XL -XC
(3.4.9)
Реактивтік кедергі
:
Қуаттың лездік мәні ток пен кернеудің лездік мәнде
P(t ) U (t ) I (t ) U m cos t I m cos( t )
Im
I ýôô
Ток күшінің әсерлік мәні:
2
Кернеудің әсерлік мәні:
U ýôô
Um
.
2
(3.4.10)
(3.4.11)
(3.4.12)
14













 Физика
Физика








