Похожие презентации:
Магнит өрісінің негізгі сипаттамалары
1. Магнит өрісінің негізгі сипаттамалары
Тәжірибедекөрсеткендей,
кеңістікте
қозғалмайтын
зарядтар
әсерінен
электростатикалық өріс пайда болады, сол
сияқты тоғы және тұрақты магниті бар
кеңістікте күш өріс пайда болады. Ол
магнитті өріс деп аталады.
2. Магнит өрісінің ерекшеліктері
• Магнитөрісі
қозғалыстағы
зарядтарға ғана әсер етеді;
• Қозғалыстағы зарядтар магнит
өрісін тудырады.
• Магнит
өрісі
тыныштықта
тұрған зарядтарға әсер етпейді.
3. Тоғы бар шеңбер (рамка) . Магнит өрісінің бағыты
• Электростатикалық өрісті зерттегендеқолданбалы нүктелік зарядты қолданған,
ал магнит өрісін зерттегенде тоғы бар
жазық контурды (тоғы бар рамка)
қолданады. Оның сызықтық өлшемі
магнит өрісін тудыратын токқа дейінгі
арақашықтығынан
аз.
Контурдың
кеңістікте
орналасуы
контурға
бағытталған нормальмен анықталады.
4. Тоғы бар шеңбер (рамка). Магнит өрісінің бағыты.
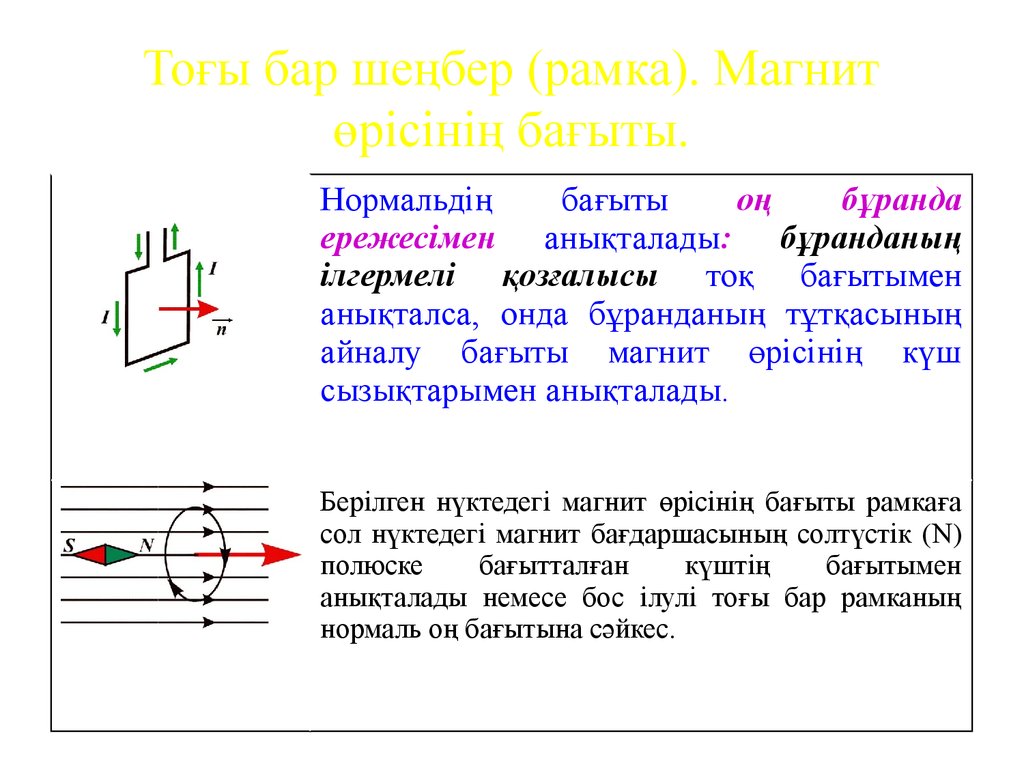
Нормальдіңбағыты
оң
бұранда
ережесімен анықталады: бұранданың
ілгермелі қозғалысы тоқ бағытымен
анықталса, онда бұранданың тұтқасының
айналу бағыты магнит өрісінің күш
сызықтарымен анықталады.
Берілген нүктедегі магнит өрісінің бағыты рамкаға
сол нүктедегі магнит бағдаршасының солтүстік (N)
полюске
бағытталған
күштің
бағытымен
анықталады немесе бос ілулі тоғы бар рамканың
нормаль оң бағытына сәйкес.
5. Тогы бар шеңбер
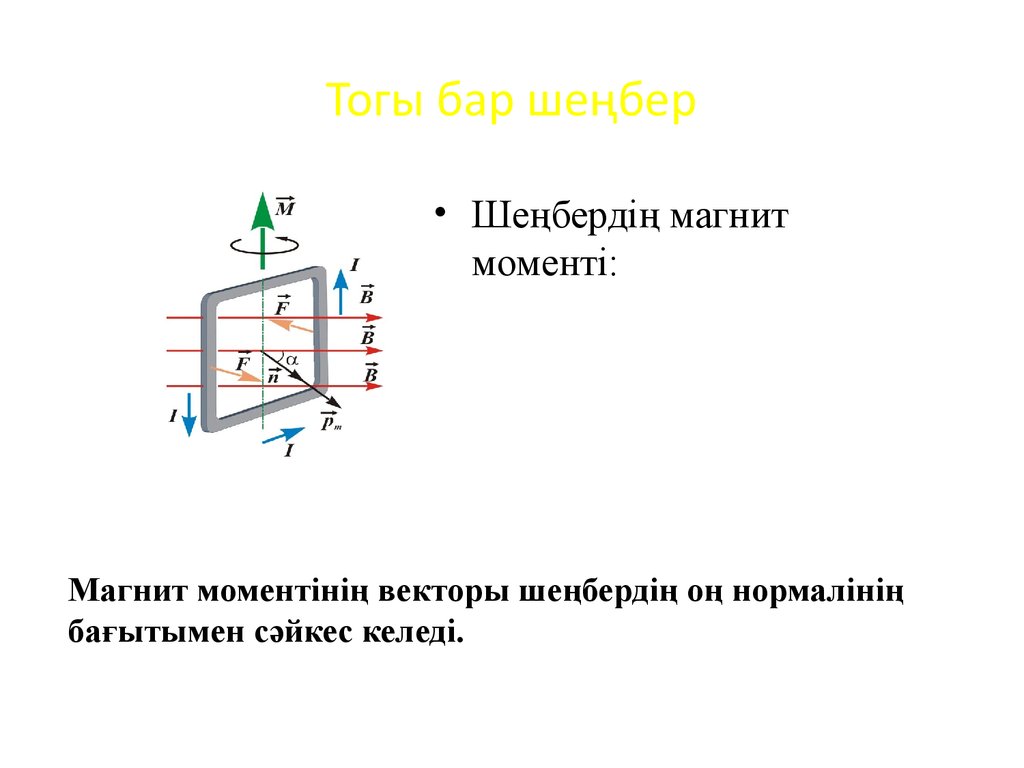
• Шеңбердің магнитмоменті:
p m ISn
Магнит моментінің векторы шеңбердің оң нормалінің
бағытымен сәйкес келеді.
6. Магнит индукция векторы
M maxB
pm
M pm B
М = Pm B sin = ISB sin ,
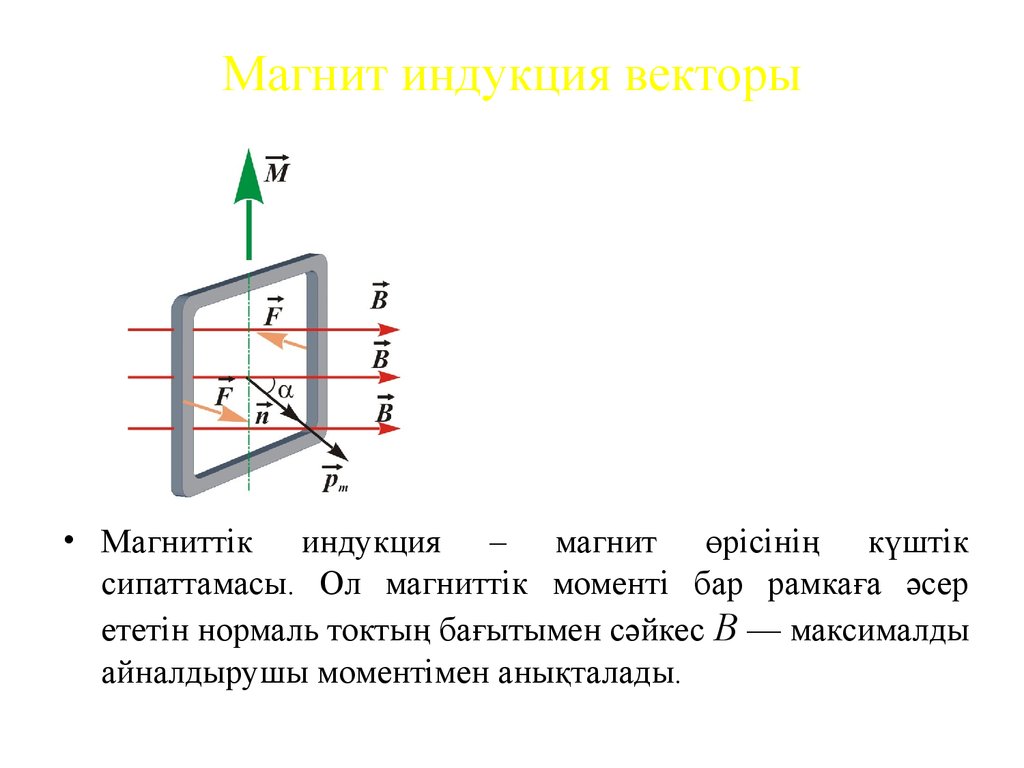
• Магниттік индукция – магнит өрісінің күштік
сипаттамасы. Ол магниттік моменті бар рамкаға әсер
ететін нормаль токтың бағытымен сәйкес В — максималды
айналдырушы моментімен анықталады.
7. Магнит индукция сызығы
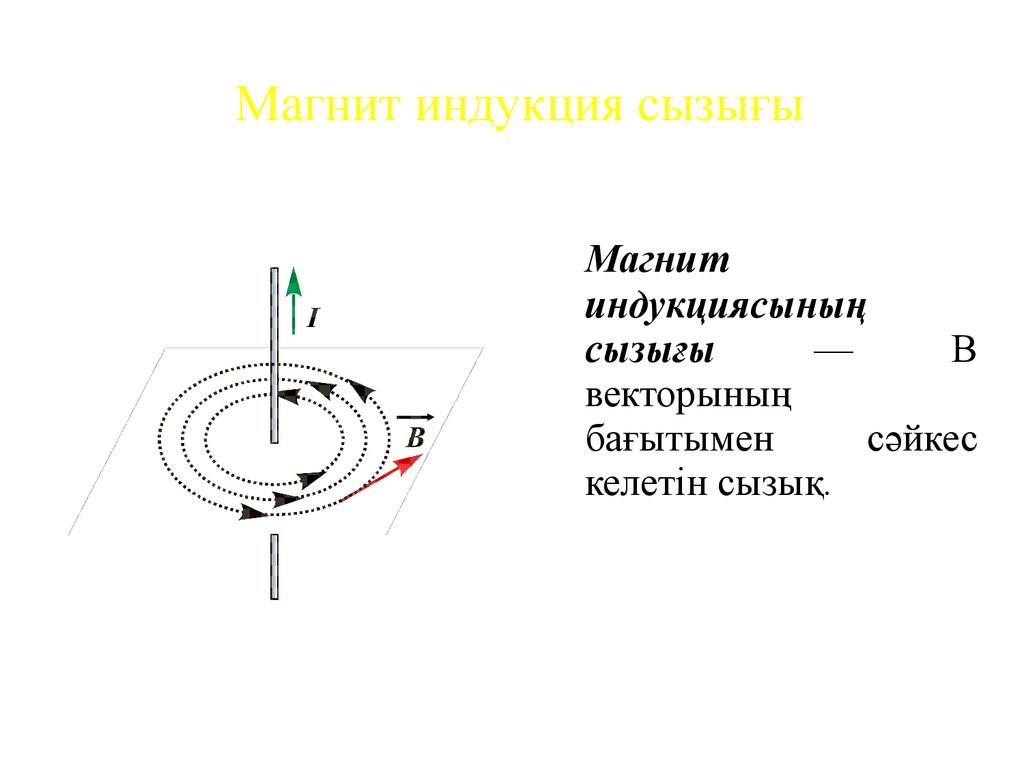
Магнитиндукциясының
сызығы
—
В
векторының
бағытымен
сәйкес
келетін сызық.
8. Макротоктар және микротоктар
макроскопиялық ток- электрлік ток, электрөткізгіштерінде жүреді, және микроскопиялық
токтар электрондардағы молекулалар мен
атомдарда болады.
• Магниттік өріс Макроток магнит өрісі магнит
кернеулігімен Н сипатталады.
• Макро және микро токтармен пайда болатын
қорытынды магнит өрісі магнит индукциясымен
В сипатталады.
9. В және Н байланысы
Біртекті изотропты орта үшінВ = 0Н,
• 0 = 4 ·10-7 Гн/м — магниттік тұрақты,
—ортаның қатысты магниттік өту
— бұл шексіз
өлшем, ортаның микротоктары әсерінен
макротоктардың магнит өрісі Н
неше есе
көбейетінін көрсетеді.
10. Магнит өрісінің суперпозиция принципі
Суперпозиция принципі: Қорытынды өрістіңмагниттік индукциясы жеке құрастырылған
өрістердің магниттік индукцияларының
векторлық қосындысына тең:
n
B Bi
i 1
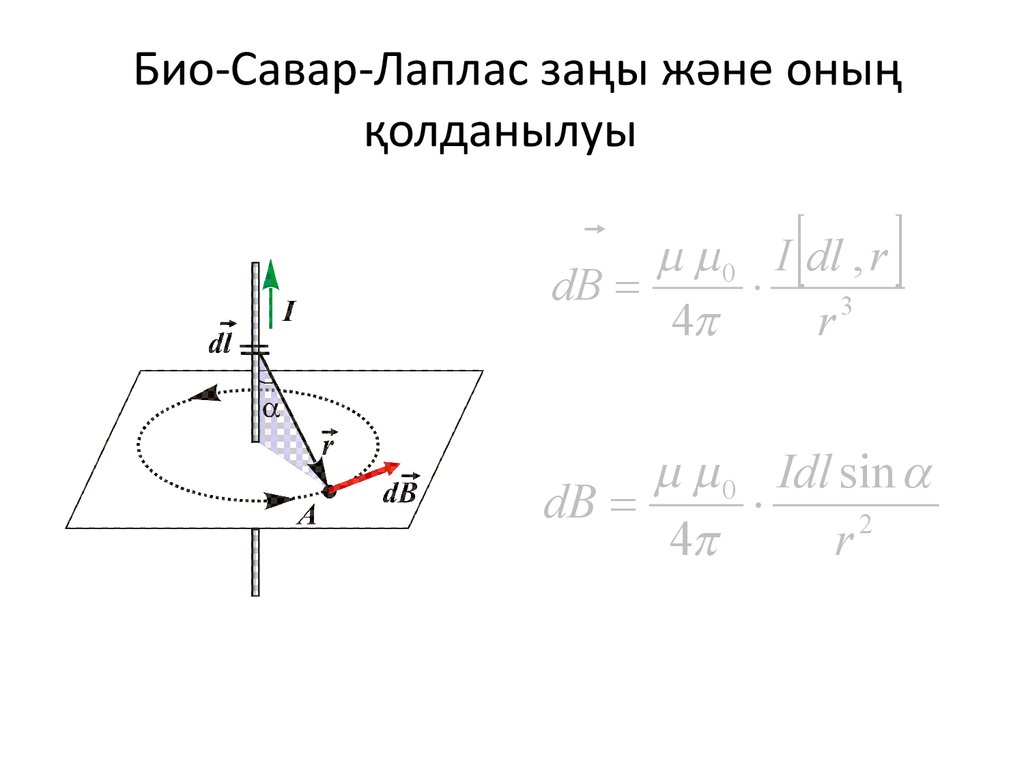
11. Био-Савар-Лаплас заңы және оның қолданылуы
0 I dl , rdB
4
r3
0 Idl sin
dB
2
4
r
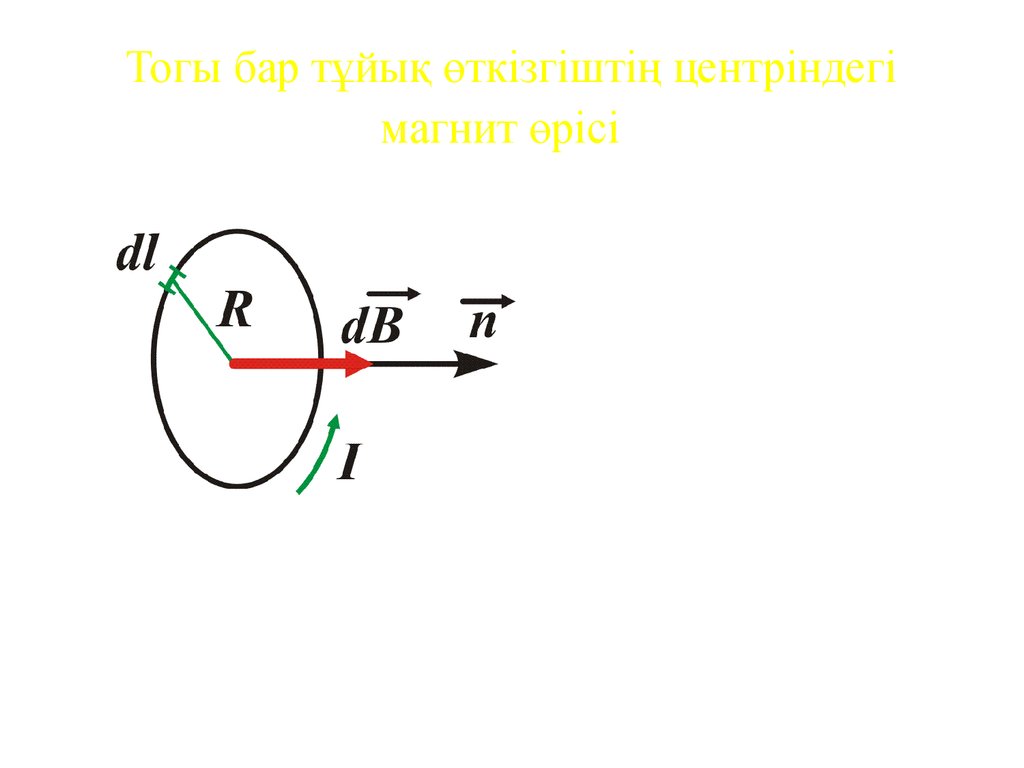
12. Тогы бар тұйық өткізгіштің центріндегі магнит өрісі
,r R2
0 I dl sin 0 I
0 I
B
dl
2
2
4
r
4 R l
2R
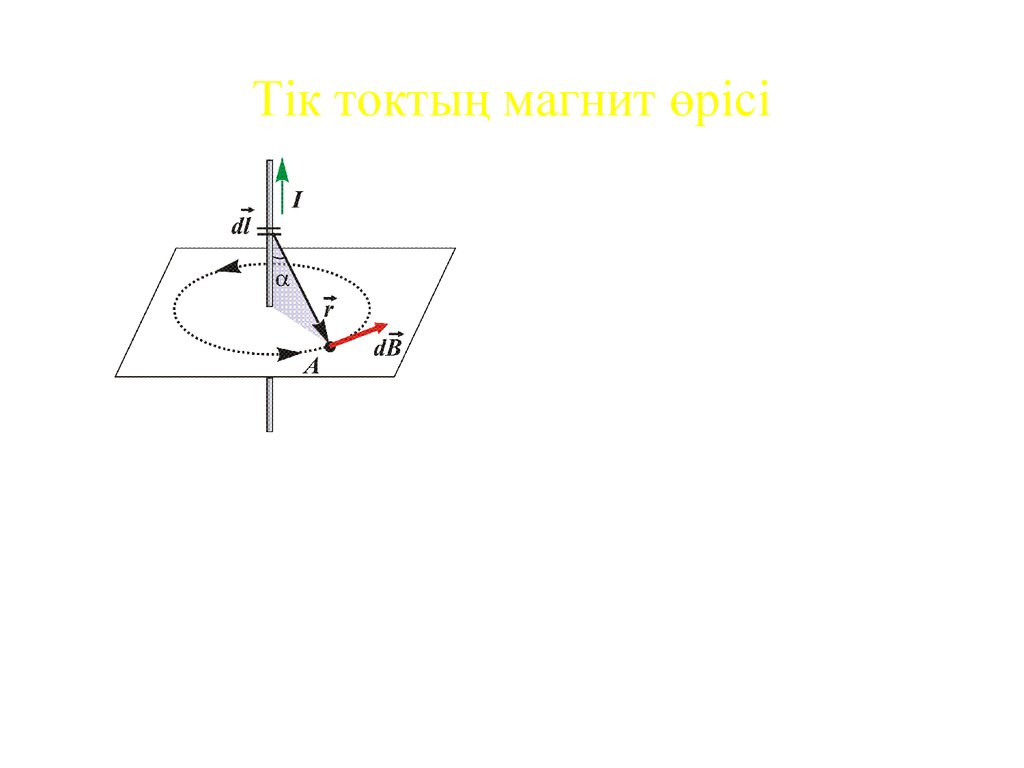
13. Тік токтың магнит өрісі
0 I dl sinB dB
2
4
r
l
l
rd
dl
;
sin
R
r
sin
0 I rd sin 0 I d sin 0 I
B
(cos 1 cos 2 )
2
4 l
r
4 l
R
4 R
B
0 I
0 I
0 I
(cos 1 cos 2 )
1 ( 1)
4 R
4 R
2 R
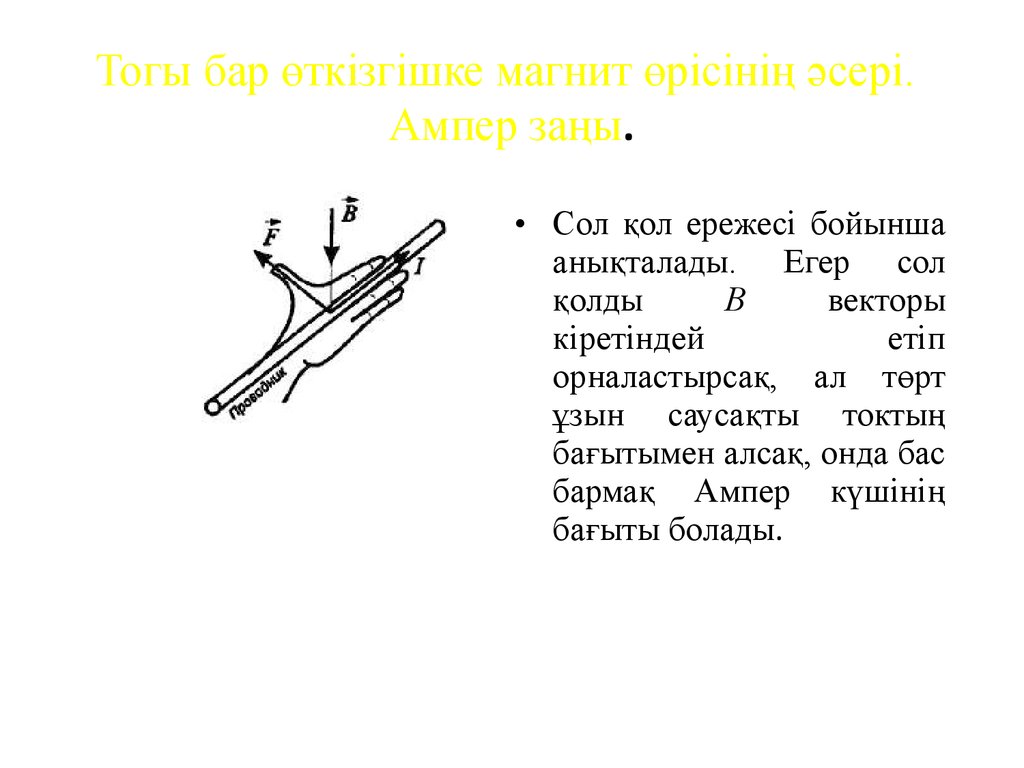
14. Тогы бар өткізгішке магнит өрісінің әсері. Ампер заңы.
dF I dl , BdF = IВdlsin
• Сол қол ережесі бойынша
анықталады. Егер сол
қолды
В
векторы
кіретіндей
етіп
орналастырсақ, ал төрт
ұзын саусақты токтың
бағытымен алсақ, онда бас
бармақ Ампер күшінің
бағыты болады.
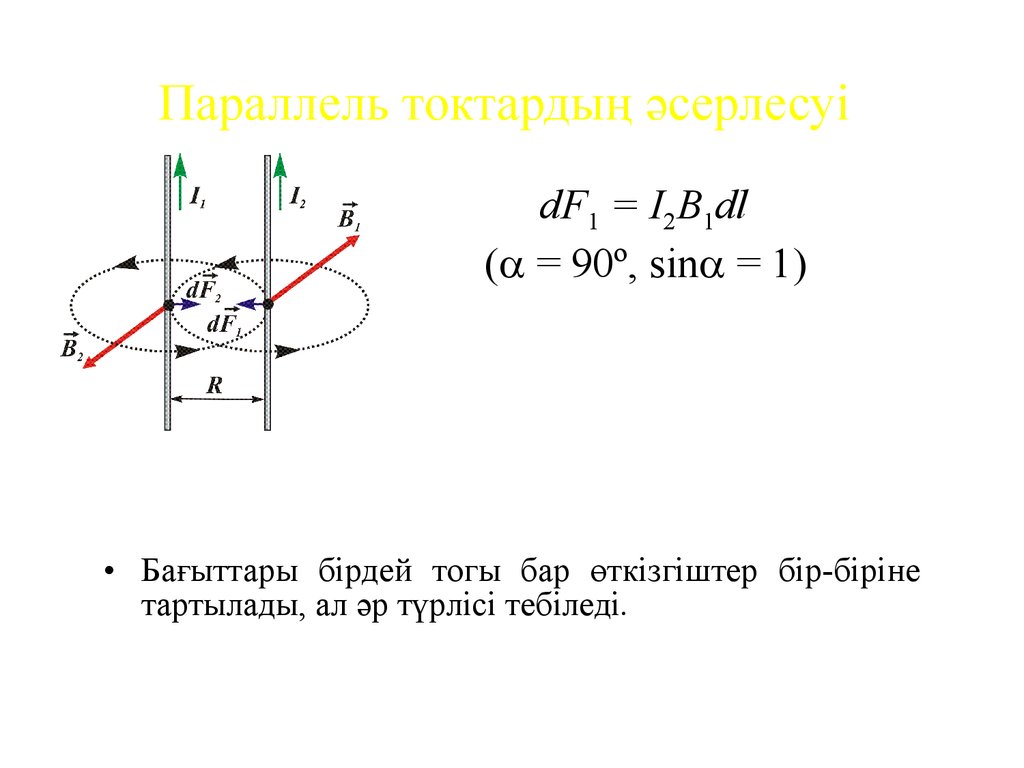
15. Параллель токтардың әсерлесуі
dF1 = I2В1dl( = 90º, sin = 1)
0 I 1
B1
2 R
0 2 I1 I 2
dF1 dF2
dl
4
R
• Бағыттары бірдей тогы бар өткізгіштер бір-біріне
тартылады, ал әр түрлісі тебіледі.
16. Магнит индукцияның және кернеудің өлшем бірліктері
dFB
Idl
Магнит индукциясының өлшем бірлігі
В — тесла (Тл)
1 Тл— Егер өткізгіште 1А ток жүрсе ,онда
осы өткізгіштің әрбір 1м-не 1Н күш әсер
ететін біртекті магнит өрісінің магнит
индукциясы.
Магнит өрісінің кернеуінің өлшем бірлігі
Н — (А/м)
B
H
0
1 А/м —өрістің кернеулігі , вакуумдағы
индукциясы - 4p· 10-7 Тл.
17. Бос жүретін зарядтың магнит өрісі
Тұрақты релятивистік жылдамдықпен жүретіннүктелік зарядтың q, магнит өрісі u (u << c)
0 q , r
B
3
4
r
0 q sin
B
2
4
r
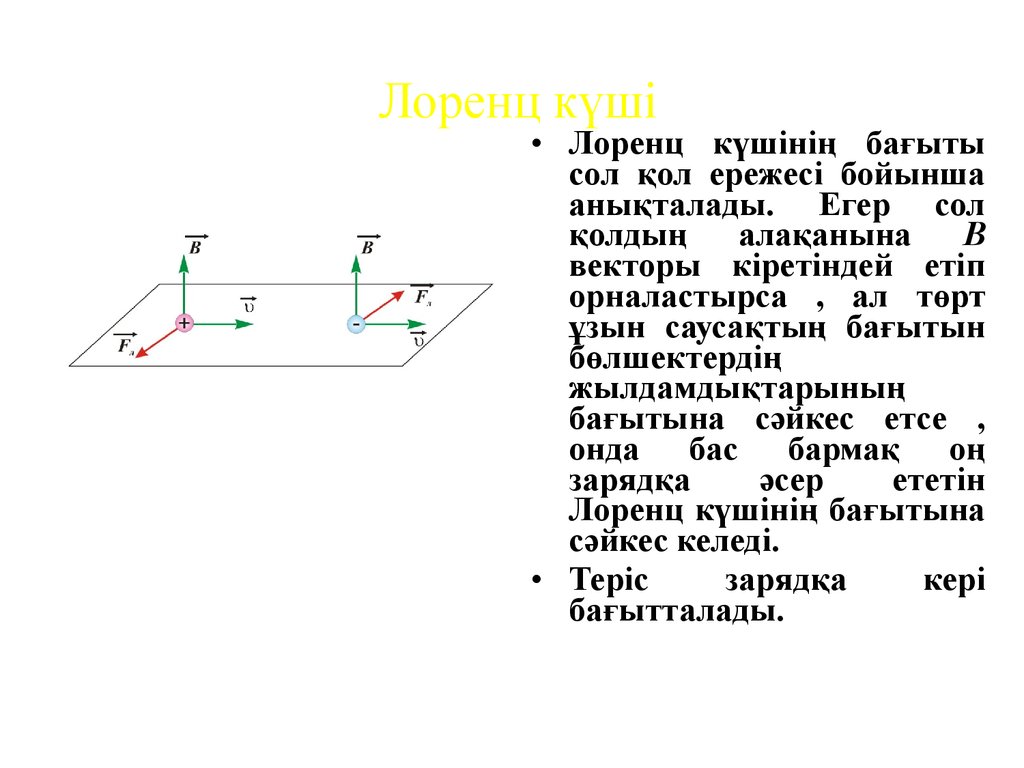
18. Лоренц күші
Fл q B sinF qE q , B
• Лоренц күшінің бағыты
сол қол ережесі бойынша
анықталады. Егер сол
қолдың алақанына
В
векторы кіретіндей етіп
орналастырса , ал төрт
ұзын саусақтың бағытын
бөлшектердің
жылдамдықтарының
бағытына сәйкес етсе ,
онда бас бармақ оң
зарядқа
әсер
ететін
Лоренц күшінің бағытына
сәйкес келеді.
зарядқа
кері
• Теріс
бағытталады.
19. Магнит өрісіндегі зарядталған бөлшектердің қозғалысы
Магнитөрісіндегі
бөлшектердің қозғалысы
зарядталған
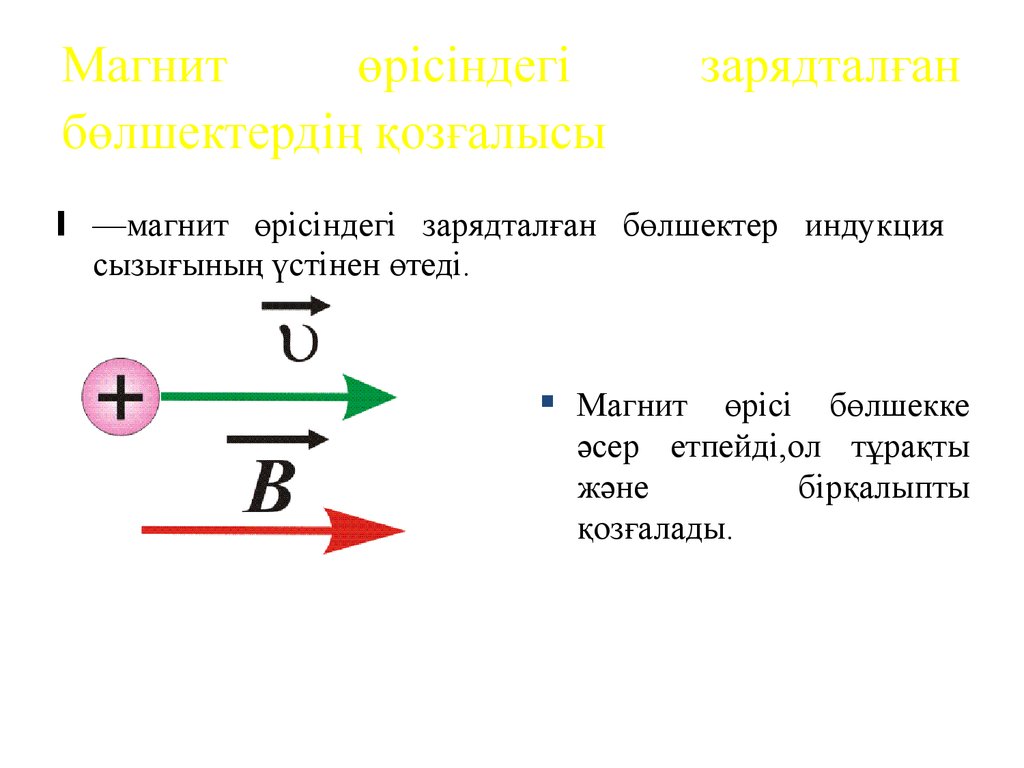
I —магнит өрісіндегі зарядталған бөлшектер индукция
сызығының үстінен өтеді.
Магнит өрісі бөлшекке
әсер етпейді,ол тұрақты
және
бірқалыпты
қозғалады.
20. Магнит өрісіндегі зарядталған бөлшектердің қозғалысы
II — Магнит өрісіндегі зарядталған бөлшектер магнитиндукция сызықтарына перпендикуляр қозғалады.
Бөлшек R радиусы бойынша айнала қозғалады:
m
R
qB
Айналу периоды :
2 R 2 m
T
qB
Бұрыштық жылдамдық:
qB qB
R
m m
21. Магнит өрісіндегі зарядталған бөлшектердің қозғалысы
III — Зарядталған бөлшектер магнит индукциясынабұрышымен қозғалады.
a
Онда бөлшектің ортақ қозғалысын қосынды ретінде алуға
болады:
1)Бірқалыпты түзусызықты қозғалыс, жылдамдығы:
|| = cos ;
2) жазықты айнала бірқалыпты қозғалыс, өріске
перпендикуляр, жылдамдығы:
┴= sin .
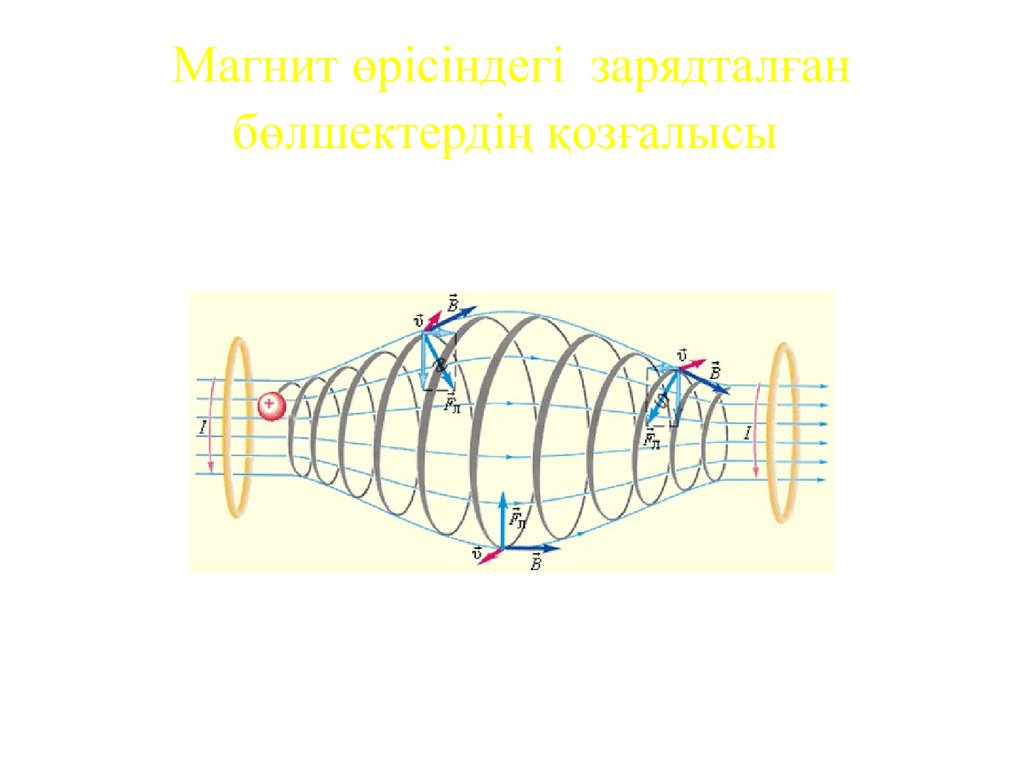
22. Магнит өрісіндегі зарядталған бөлшектердің қозғалысы
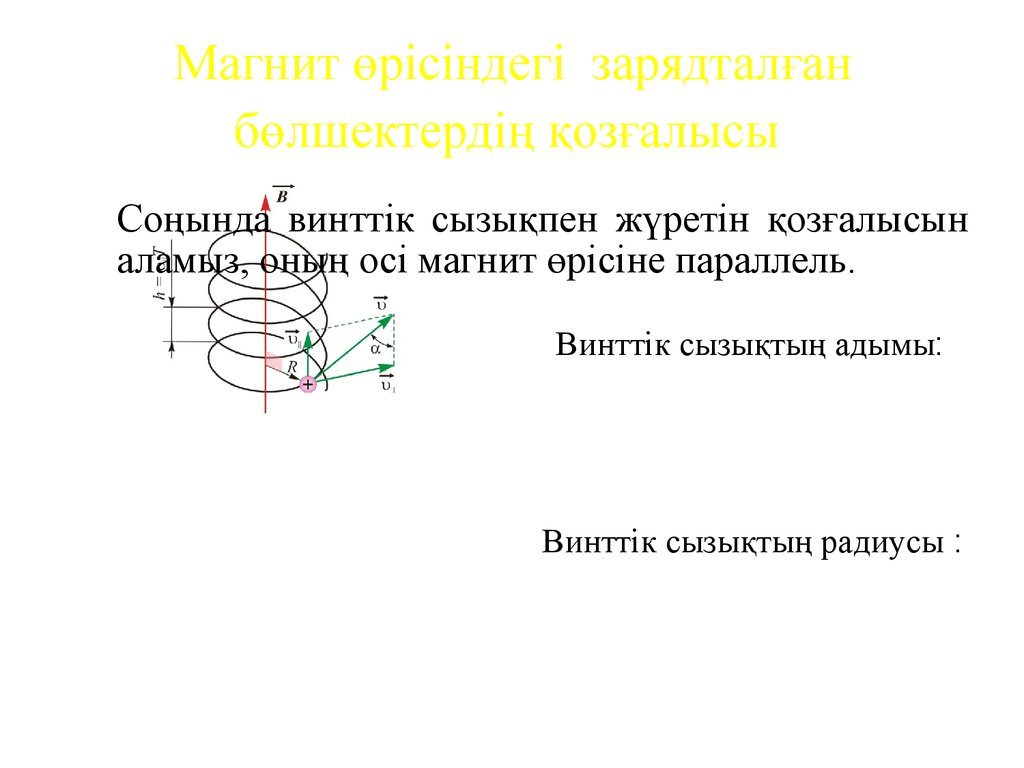
Соңында винттік сызықпен жүретін қозғалысыналамыз, оның осі магнит өрісіне параллель.
Винттік сызықтың адымы:
h = υ || T = υ T cos
R
m
qB
Винттік сызықтың радиусы :










 Физика
Физика








