Вынужденные колебания системы с одной степенью свободы

1.

Московский государственный университет путей
сообщения
Вынужденные колебания системы с
одной степенью свободы
Курбацкий Евгений Николаевич
профессор кафедры “Мосты и тоннели”,
д.т.н.

2.

Вынужденные гармонические колебания
системы с одной степенью свободы с учётом
вязкого демпфирования
mu(t ) cu(t ) ku(t ) P sin t
P
u(t ) 2 0u(t ) u(t ) sin t
m
k
с
2
0 ; ; ссr 2m ;
m
ссr
2
0
ui
2
ln
ui 1
1 2
2

3.

Принятые обозначения
P аплитуда вынуждающей гармонической силы;
частота вынуждающей гармонической силы;
0 частота собственных колебаний системы
без учёта сил сопротивления;
D частота собственных колебаний системы
c учётом сил сопротивления D 0 1 ;
2
относительный коээфициент демпфирования;

4.

Некоторые сведения из краткого курса
математического анализа
P
u (t ) 2 0u (t ) u (t ) sin t (1)
m
2
u (t ) 2 0u (t ) 0 u (t ) 0
(2)
2
0
Общее решение уравнения с правой частью (1)
можно составить как сумму общего решения
соответствующего уравнению без правой части (2) и
какого либо частного решения данного уравнения (1)

5.

Общее решение однородного и
неоднородного дифференциального
уравнения
P
u (t ) 2 0u (t ) u(t ) sin t (1)
m
u p (t ) C sin t D cos t
2
0
u (t ) 2 0u (t ) u (t ) 0
2
0
Acos D t B sin D t
u (t ) e t Acos D t B sin D t
uc (t ) e
0 t
0
C sin t D cos t
(2)

6.

Определение констант А и В однородного
дифференциального уравнения
u u(0) u u u(0)
u(t ) 2 0u(t ) u(t ) 0
2
0
uc (t ) e
0 t
A u (0);
u (t ) e
0t
(2)
Acos D t B sin Dt
B
u (0) 0u(0)
D
u (0) 0u(0)
sin D t
u (0)cos D t
D

7.

Определение констант С и D решения
неоднородного дифференциального
уравнения
P
2
u(t ) 2 0u(t ) 0 u(t ) sin t ( a )
m
u p (t ) C sin t D cos t
( b)
Подставив (а) в (b), получим
02 2 C 2 0 D sin t
P
2 0 C C
D cos t sin t
m
2
0
2

8.

Для определение констант С и D приравняем
коэффициенты левой и правой части уравнения
при одинаковых тригонометрических функциях
02 2 C 2 0 D sin t
P
2 0 C D cos t sin t
m
2
0
2
Получим систему уравнений:
P
C 2 0 D m
2
2
2 0 C 0 D 0
2
0
2

9.

Общее решение дифференциального уравнения
колебаний системы с одной степенью свободы при
гармоническом воздействии с учётом сил
сопротивления пропорциональных скорости
Обозначим :
o
u (t ) e
0t
A sin D t B cos D t
C sin t D cos t;
P
1
P
2
С
; D
;
2
2
2
2
k 1 2 2
k 1 2 2
2

10.

Колебания с частотой вынуждающей силы
u (t ) e
0t
A sin D t B cos D t
C sin t D cos t;
при t e
Aв С D
2
0t
2
0 u (t ) C sin t D cos t
C
D
sin и
co s
Aв
Aв
u (t ) Aв cos sin t sin cos t
u (t ) Aв sin t

11.

Вынужденные колебания системы с одной
степенью свободы при гармоническом
воздействии с учётом сил сопротивления
пропорциональных скорости

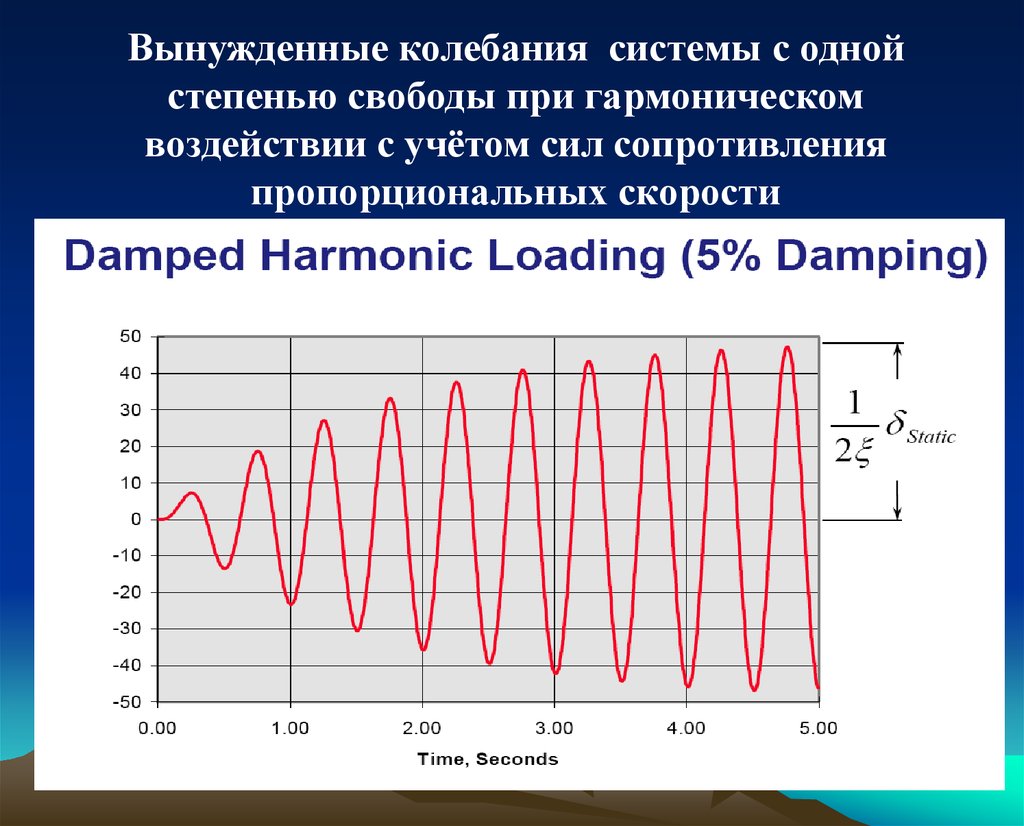
12.

Вынужденные колебания системы с одной
степенью свободы при гармоническом
воздействии с учётом сил сопротивления
пропорциональных скорости

13.

Вынужденные колебания системы с одной
степенью свободы при гармоническом
воздействии с резонансной частотой

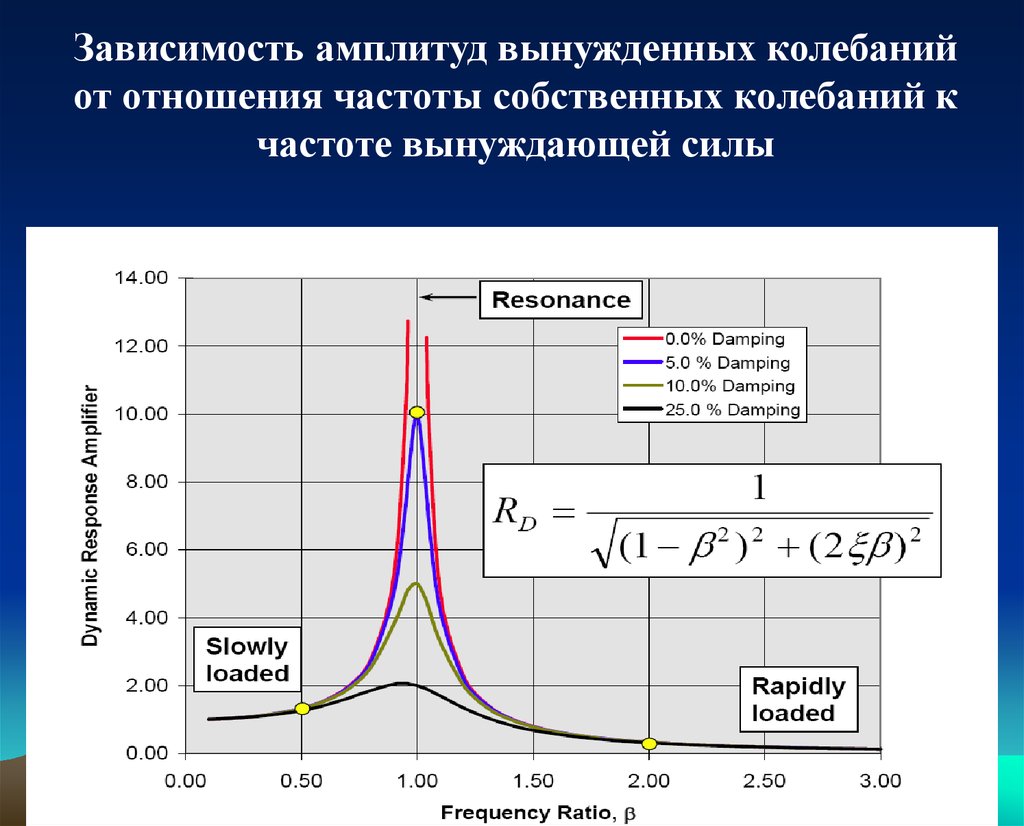
14.

Зависимость амплитуд вынужденных колебаний
от отношения частоты собственных колебаний к
частоте вынуждающей силы

15.

Заключение
При частоте возмущающей силы близкой к
собственной частоте амплитуды вынужденных
колебаний возрастают и превышают статические.
Такое явление называется резонансом.
В
системах
с
малым
коэффициентом
демпфирования амплитуды при резонансах могут
достигать больших значений.
Демпфируемые системы при резонансе имеют
ограниченные амплитуды:
umax ust 1 / 2

16.

Реакция системы с одной степенью
свободы на импульс
u (t ) 2 0u(t ) 02 u (t ) 0
Решение при начальныхусловиях : u (0) и u (0)
u (t ) e
0t
u (0) 0 u(0)
sin D t
u (0) cos D t
D
при u (0) 0,
u (t ) e
0t
u(0)
D
sin D t

17.

Дифференциальное уравнение системы при
импульсивном воздействии можно записать,
используя обобщённые функции
mu (t ) cu (t ) ku (t ) mu (0) (t )
u (t ) 2 0 u (t ) 02 u (t ) u (0) (t )
где (t ) дельта функция Дирака ,
имеет размерность 1 / сек и
обладает следующими свойствами :
(t ) 0 при t 0; (t ) при t 0;
(t )dt 1

18.

Реакция системы с одной степенью
свободы на произвольное воздействие
mu (t ) cu (t ) ku (t ) P (t );
u (0) 0; u(0) 0;
Для определения решения произвольная сила
рассматривается как последовательность импульсов бесконечно малой продолжительности.

19.

Реакция системы с одной степенью
свободы на единичный импульс
Рассмотрим силу, действующую в момент
времени t в течении малого интервала времени
p (t ) 1 / ;
При 0
величина силы становится
бесконечно большой но интеграл по времени
остаётся равным единице. Такую силу называют
единичным импульсом.
Смещённая дельта функция Дирака (t )

20.

Если на массу в момент времени t
в
течении бесконечно малого интервала времени
действует
единичный
импульс,
масса
приобретает начальную скорость , определяемую
выражением
1
u( )
m
При этом ни пружина, ни демпфер не успевают
среагировать. Поэтому в момент времени t
Можно сформулировать следующие
условия:
1
u( ) 0
u( )
m
начальные

21.

При таких начальных условиях уравнение
движения массы при действии единичного
импульса можно записать в виде:
1 0 ( t )
u (t )
e
sin D (t )
m D
При отсутствии сил вязкого сопротивления:
1
u (t )
sin 0 (t )
m 0

22.

При действии произвольной силы необходимо
проинтегрировать реакции от единичных импульсов, увеличенных на значения силы. Интеграл
Дюамеля
t
1
u (t )
m D
p( )e
0 ( t )
sin D (t ) d
0
При отсутствии сил вязкого сопротивления:
t
1
u (t )
p ( )sin 0 (t ) d
m 0 0

23.

Некоторые начальные сведения теории
интегрального преобразования Фурье
Преобразованием Фурье функции u (t )
называется интеграл, определяемый
выражением F u (t )
u(t )e
i t
dt u ( )
При решении динамических задач
преобразование Фурье или интеграл Фурье
является одним из основных математических
аппаратов

24.

Некоторые начальные сведения теории
преобразования Фурье (продолжение)
Если функция u ( ) является преобразованием
(изображением ) Фурье функции u (t )
тогда
изображение Фурье производной этой функции по
времени определится выражением:
F u (t ) ( i )u ( )
второй производной выражением:
F u (t ) ( i ) u ( )
2

25.

Некоторые начальные сведения теории
преобразования Фурье (продолжение)
Таким образом дифференцированию
функции u (t ) во временной области
соответствует умножению функции
u ( ) на множитель ( i )
n
d u (t )
n
( i ) u ( )
n
dt

26.

Пример использования
преобразования Фурье
Дифференциальное уравнение колебаний
системы с одной степенью свободы при
сейсмическом воздействии имеет вид
u (t ) 2 0u (t ) 02u (t ) u g (t )
Применим преобразование Фурье к обеим частям
уравнения обозначив u ( ) изображение Фурье
неизвестной функции u (t ) . Получим
( i ) u ( ) 2 0 ( i )u ( ) u ( ) F u g (t )
2
2
0

27.

Пример использования
преобразования Фурье (продолжение)
( i ) u ( ) 2 0 ( i )u ( ) u ( ) F u g (t )
2
2
0
u ( ) 2 2i 0 02 F u g (t )
Выполнив необходимые преобразования,
получим изображение Фурье искомой
функции
F u g (t )
u ( ) 2
2i 0 02

28.

Для определения функции u (t ) необходимо
выполнить обратное преобразования Фурье
1
u (t )
2
1
u( )
2
i t
u
(
)
e
dt
u g (t )e
2
i t
2i 0
2
0
d
Обратное преобразования Фурье можно получить,
используя стандартную программу быстрого
преобразования Фурье FFT, или получить
аналитическое выражение, используя различные
методы интегрирования

29.

Сдвиг во времени
Воздействие на разные опоры сооружения
может отличаться во времени из за более
позднего прихода сейсмических волн
Преобразование Фурье позволяет довольно
просто учитывать это явление. Так как
сдвигу функции во временной области
соответствует умножение на экспоненту в
области изображений.
il
l
F u g (t ) F u g (t ) e

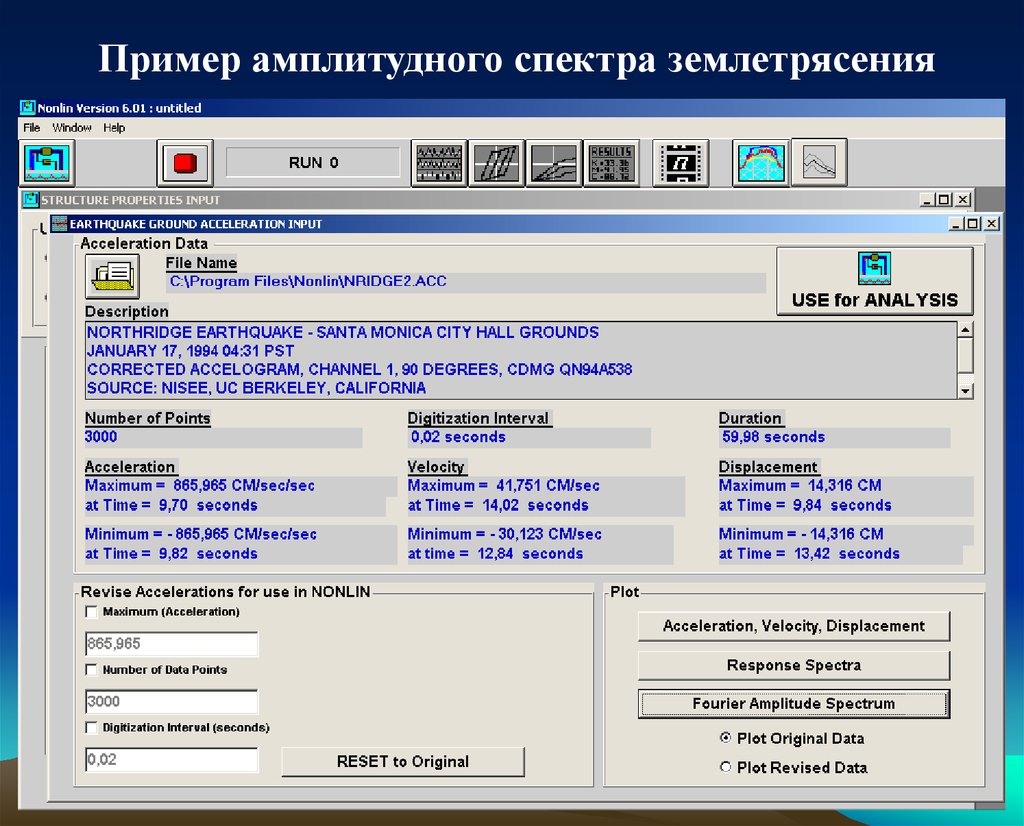
30.

Пример амплитудного спектра землетрясения

31.

Графики ускорений, скоростей и перемещений
поверхности грунта при землетрясении

32.

Амплитудный спектр землетрясения Northridge
earthquake Santa Monica City Hall

33.

СВОБОДНЫЕ КОЛЕБАНИЯ
Исходные данные :
высота колонн: l 5 м ;
жёсткость колонны при изгибе : EI 20 108 Нм2 ;
масса пролёта: m 6 10 4 кг ;
массой колнн можно пренебречь.
u g ur
ua
l
EI
l
EI
l
Расчётная схема

34.

Исходные данные
1. Определение жёсткости колон при изгибе (см. лекцию №2):
k
l
EI
l
12EI
l3

35.

Исходные данные
Вариант 1
Жёсткое закрепление обеих концов колон.
Жесткость эквивалентной пружины 12 EI 24 20 108
8
kж 2 3
3.84
10
N/м
3
l
5
Масса пролётного строения - m 6 104 кг
Частота собственных колебаний
kж
3.84 108
n
80,0 рад / сек
4
m
6 10

36.

Исходные данные
Вариант 2
Жёсткое закрепление обеих концов колон.
Жесткость эквивалентной пружины 12 EI 24 20 108
6
kж 2 3
48.0
10
N/м
3
l
10
Масса пролётного строения - m 6 104 кг
Частота собственных колебаний
kж
48.0 106
n
28, 28 рад / сек
4
m
6 10

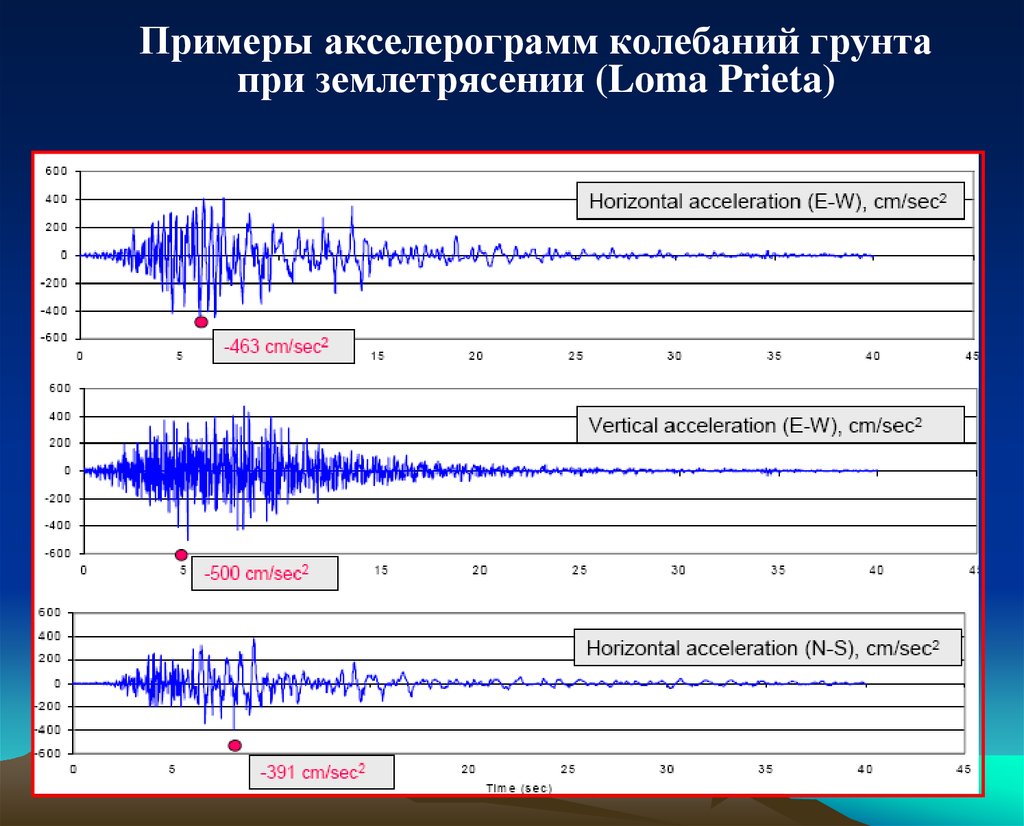
37.

Примеры акселерограмм колебаний грунта
при землетрясении (Loma Prieta)