Свободные и вынужденные колебания системы с бесконечным числом степеней свободы

1. Лекция 19-20. Свободные и вынужденные колебания системы с бесконечным числом степеней свободы

Содержание
1.Продольные
и
поперечные
колебания
стержня
с
распределенной массой.
2.Расчет
рам
методом
перемещений.
3.Расчет ферм методом сил.

2. Продольные колебания стержней

dm=ρAdx
ρ- плотность материала, А – площадь поперечного сечения
N1
dx I 0,
x
N1
u
N
dm u //
dx,
,
x
x
EA
2u
2u
x 2
E t 2
N1 N 1

3. Гармонические колебания стержня

d2X
2
X 0,
2
E
dx
X ASin (
2
E
x) BCos (
2
E
x)
u=Xsinωt
левый конец стержня –защемлен, а правый – свободен
x l
x 0
u X
0,
x x
u
u X 0
0
x
N 0,
2l
n 1,
если
mi n
( 2 n 1)
2l
E
E
,

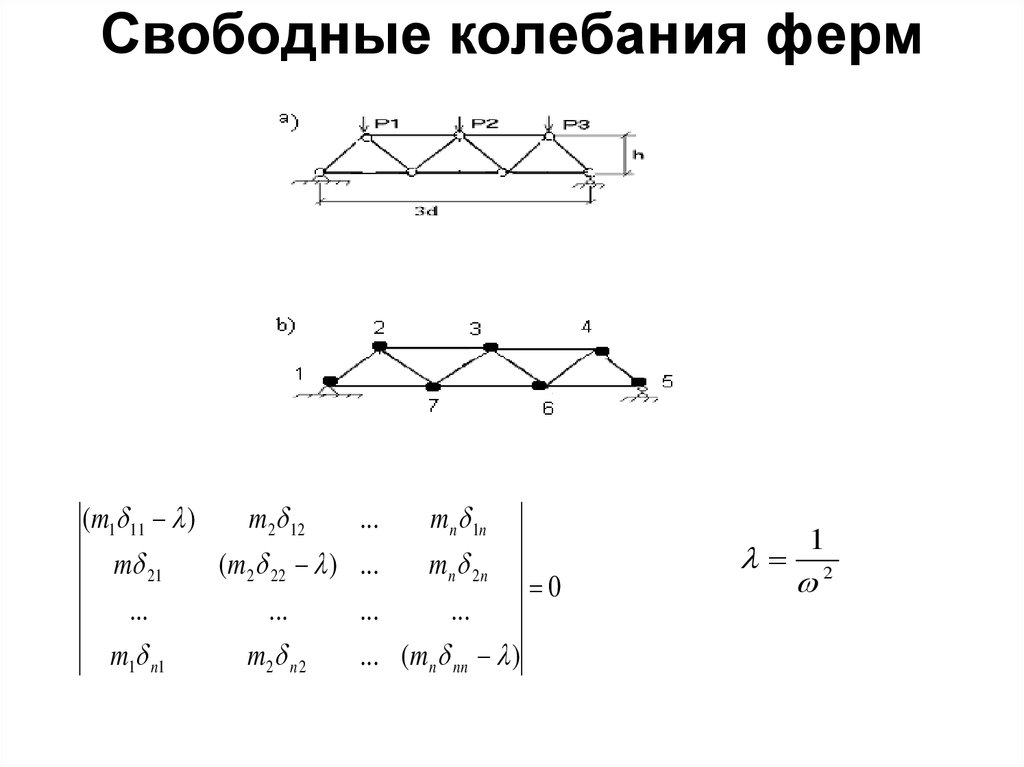
4. Свободные колебания ферм

(m1 11 )
m 21
m 2 12
...
(m 2 22 ) ...
...
...
m1 n1
m 2 n 2
...
m n 1n
mn 2n
...
... (m n nn )
0
1
2

5. Уравнения динамического равновесия

mk x N kt Cos kt
//
k
mk y k// N kt Sin kt

6. Определение частоты свободных колебаний

xk ak Sin ( i t i ), yk bk Sin ( i t i ),
x x ,
//
k
y yk
2
i k
//
k
2
i
EFki
mk x
Cos ki ( xi xk ) Sin ki ( yi yk ) Cos ki ,
lki
2
i k
EFki
mk y
Cos ki ( xi xk ) Sin ki ( yi yk ) Sin ki
lki
2
i k

7. Вынужденные колебания ферм при вибрационной нагрузке

Z1 ( 11
1
m1
2
) Z 2 12 ... Z n 1n Po 1 p 0,
Z1 21 Z 2 ( 22
1
m2 2
) ... Z n 2 n Po 2 p 0,
.........................................................................,
Z1 n1 Z 2 n 2 ... Z n ( nn
11* 11
1
mn
2
) Po np 0
1
1
1
*
*
;
.
;
nn
nn
2
22
22
2
2
m1
mn
m2
Zkx mk 2 xk ,
Zky mk 2 yk

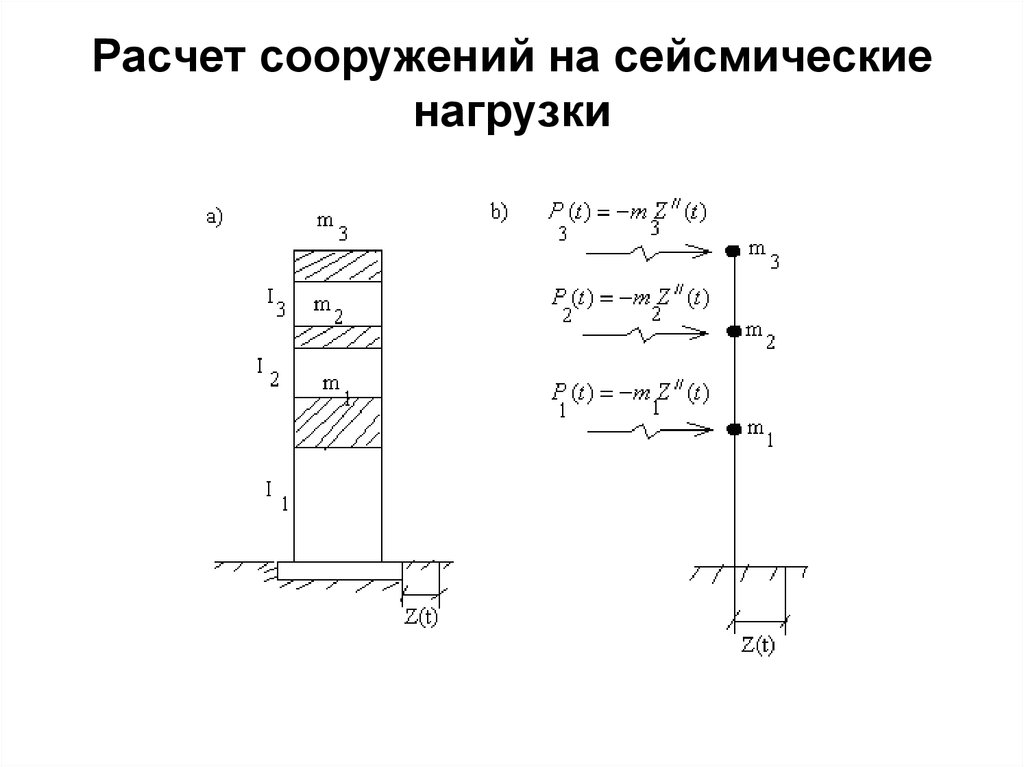
8. Расчет сооружений на сейсмические нагрузки

9. Определение собственных частот и форм колебаний

m1 11
m2 12
m3 13
m1 21
m2 22
m3 23
m1 31
m2 32
m3 33
n
X k xki Sin ( i t ),
0
k 1,2,3
1
x1i
1i 1,
x1i
x2 i
2i ,
x1i
x11
X 1 x12 ,
x 21
X 2 x 22 ,
x13
x 23
x3i
xni
3i , ... ni ,
x1i
x1i
x31
X 3 x32
x33

10. Составляющие сейсмической нагрузки

s11
P1 S1 s12 ,
s13
s21
P2 S 2 s22 ,
s23
s31
P3 S 3 s32
s33