Вынужденные механические колебания

1. Вынужденные механические колебания

Рассмотрим систему, на которую, кроме упругой силы (– kx)
и сил сопротивления (– r∙υ), действует добавочная периодическая сила F – вынуждающая сила.
Для колебаний вдоль оси x запишем:
max = −kx − rυx + Fx
(7.1)
– основное уравнение колебательного процесса, или
d 2x
dx
(7.2)
2
dt
2
2
dt
0 x f x
где fx = Fx/m – вынуждающая сила, изменяющаяся по гармоническому закону: fx = F0 cosωt.
Через некоторое время после начала действия вынуждающей силы колебания системы будут совершаться с частотой
вынуждающей силы ω. Уравнение установившихся вынужденных колебаний:
X=Asin(ωt+φ)
(7.3)

2.

Задача: найти амплитуду А и разность фаз φ между
смещением вынужденных колебаний и вынуждающей силой.
Воспользуемся тем, что скорость на π/2 опережает
смещение, а ускорение на π/2 опережает скорость:
dx
x
A cos( t ),
dt
d x
ax
2 A sin( t ) 2 A cos( t / 2).
dt
x A sin( t ) A cos( t / 2).
Подставим эти уравнения в уравнение (7.2)
F0
2
A cos t 0 2 A cos( t ) 0 A cos t cos t ,
2
2 m
2

3.

F0
2
cos t 0 2 cos( t ) 0 cos t
cos t
2
2 mA
2
Каждое слагаемое этого уравнения можно представить в
виде соответствующего вращающегося вектора амплитуды:
A1 = ω2 – амплитуда ускорения; A2 = 2βω – амплитуда скорости; A3 = ω02 – амплитуда смещения; A4 = F0 /mA – амплитуда вынуждающей силы, причем A3 > A1 .
Вектор амплитуды
силы
найдем по правилу сложения векA4 A1 A2 A3
торов:
Из рисунка видно, что
A42 ( A3 A1 ) 2 A22
Тогда
F0
F0
A
,
2
2
mA4 m ( A3 A1 ) A2
A
F0
m ( ) 4
2
0
2 2
2
2
.

4.

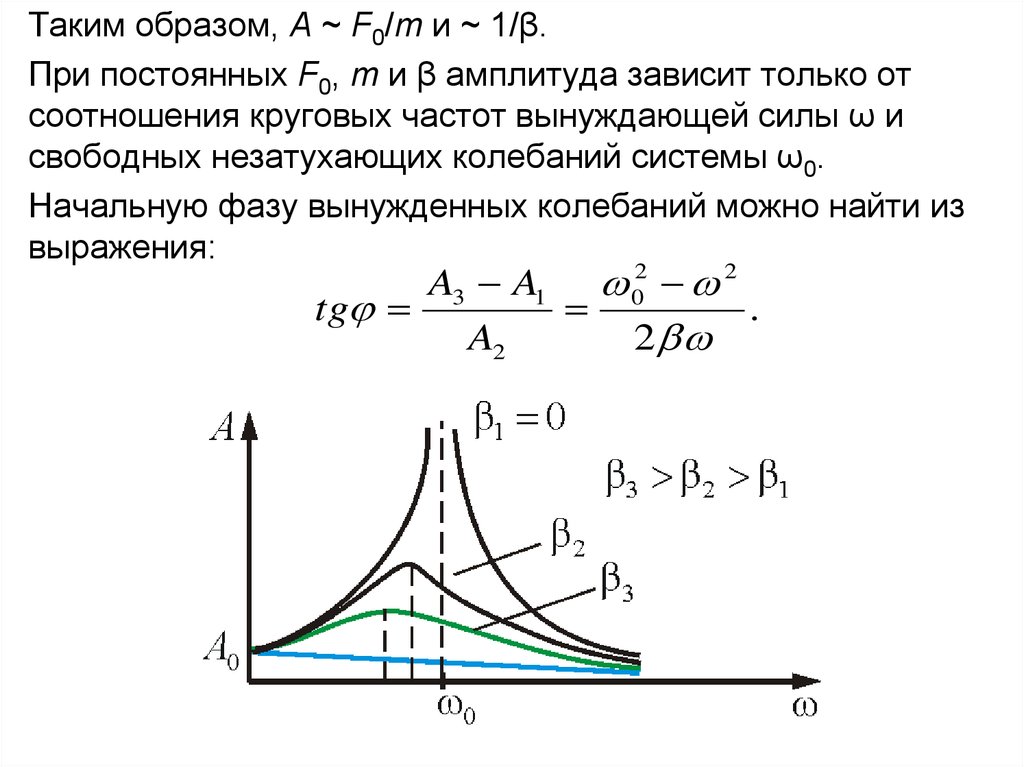
Таким образом, A ~ F0/m и ~ 1/β.
При постоянных F0, m и β амплитуда зависит только от
соотношения круговых частот вынуждающей силы ω и
свободных незатухающих колебаний системы ω0.
Начальную фазу вынужденных колебаний можно найти из
выражения:
A3 A1 02 2
tg
.
A2
2

5.

6.

7.

г) физический маятник
Физический маятник – твердое тело, которое может совершать
колебания под действием собственной силы тяжести mg вокруг
неподвижной горизонтальной оси, не проходящей через центр
масс тела и называемой осью качания. Центр тяжести маятника
совпадает с его центром масс. Как правило, силой трения в подвесе маятника пренебрегают и момент относительно оси качания
маятника создает только его сила тяжести mg.
При отклонении маятника на угол α момент,
создаваемый силой тяжести равен:
M = mgd sinα .
Согласно основному уравнению динамики
вращательного движения (для тела с моментом инерции I, вращающегося вокруг неподвижной оси в отсутствие трения):
M J J
2
t
2
mgd sin .
При малых α → sinα ≈ α
→
2
t 2
mgd
0
J

8.

Сравнивая с уравнением свободных незатухающих гармонических
колебаний: d2x/dt2 + ω2x = 0 , имеем для физического маятника:
mgd
,
J
J
T 2
.
mgd
Предельным случаем физического маятника является математический маятник - материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости под действием силы тяжести. Вся масса сосредоточена в
центре масс тела. При этом d=l – длина маятника и момент инерции J = ml2. Тогда
mgl
ml
2
g
,
l
l
T 2
g
Длина математического маятника, имеющего такой же период колебаний, что и данный физический маятник, называется приведенной длиной физического маятника. Точка О1, находящаяся на
расстоянии lпр от точки подвеса О маятника, называется центром
качания физического маятника. Точки O и О1 обладают свойством
взаимности, т.е. при перемене их ролей длина и период маятника
останутся прежними.

9.

Свободные гармонические колебания в электрическом
колебательном контуре
Простейшим колебательным контуром является замкнутая цепь,
состоящая из емкости C и катушки индуктивности L.
По закону Ома для замкнутой цепи: сумма падений
напряжений на проводниках сопротивлением R и на
конденсаторе Uс равна ЭДС самоиндукции в контуре
IR + Uc = IR + Q/C = εsi = -L(dI/dt).
I = dQ/dt → dI/dt = d2Q/dt2,
d 2Q
dt
2
R dQ
1
Q 0
L dt
LC
1
LC
,
(R→0) → d2Q/dt2 + ω2Q =0
T 2 / 2 LC.
Q =Qmsin(ωt + φ0) и I = dQ/dt = ωQmcos(ωt + φ0) = Imcos(ωt + φ0)
W = Wэл + Wмагн = (1/2)∙(LI2 + CU2)

10. Сложение гармонических колебаний. Фигуры Лиссажу

Сложение колебаний – нахождение значения результирующих колебаний системы при ее участии в нескольких колебательных
процессах. Различают сложение сонаправленных и взаимноперпендикулярных колебаний.
Используем метод векторных
диаграмм.
x1 = A1sin(ω1t + φ1) = A1sinФ1(t)
x2 = A2sin(ω2t + φ2) = A2sinФ2(t)
Результирующее колебание: x = x1 +x2 = AsinФ(t) , где амплитуда
A2(t) = A12 + A22 + 2A1A2cos(Ф2 –Ф1)
A1 sin Ô1 (t ) A2 sin Ô 2 (t )
tgÔ (t )
.
Ax A1 cosÔ1 (t ) A2 cosÔ 2 (t )
Ay

11.

Когерентными называются колебания, разность фаз которых во
времени постоянна; т.к. Φ(t) = (ω2 − ω1)t + (ϕ2 − ϕ1 ) = const , то это
выполняется при ω2= ω1= ω, тогда x = x1+ x2= Asin(ωt+ϕ0), где
амплитуда А и фаза Ф результирующего колебания. Тогда в зависимости от значения (ϕ2 −ϕ1) результирующая амплитуда А
изменяется в пределах от A = |A1 − A2| при ϕ2 -ϕ1 = ±(2m +1)π, до A
= |A1 + A2| при ϕ2 -ϕ1 = ±2 π m (m → целые числа).
При ϕ2 -ϕ1 = ±2 π m колебания называются синфазными (в одной
фазе), а при ϕ2 -ϕ1 = ±(2m +1)π – противофазными.
При ω1 ≠ ω2 результирующий вектор A будет изменяться по длине
и вращаться с переменной скоростью. При сложении колебаний с
близкими частотами (Δω=|ω2 −ω1|<<ω) возникают, так называемые, биения, тогда x1 = xmcosωt,
x2 = xmcos(ωt + Δωt).
x(t ) x1 x2 2 xm cos
t t t
cos
t t t
2
t
2 xm cos t cos
xm cos t
2
2

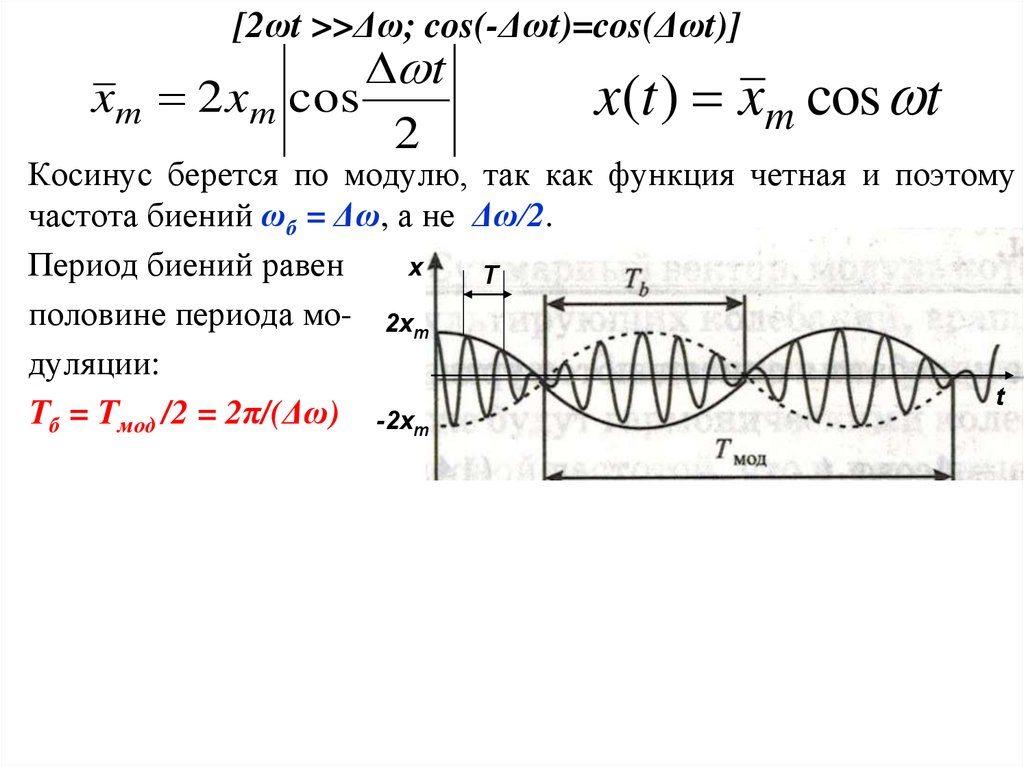
12.

[2ωt >>Δω; cos(-Δωt)=cos(Δωt)]
t
xm 2 xm cos
2
x(t ) xm cos t
Косинус берется по модулю, так как функция четная и поэтому
частота биений ωб = Δω, а не Δω/2.
x
Период биений равен
T
t
xm 2 xm cos
2
половине периода мо- 2xm
дуляции:
t
Тб = Тмод /2 = 2π/(Δω) -2xm