Похожие презентации:
Электр тізбектерінің пассивтік бөліктерін эквивалентті түрлендіру. Тұрақты токтың қарапайым тізбектерін есептеу әдістері
1. Электр тізбектерінің пассивтік бөліктерін эквивалентті түрлендіру. Тұрақты токтың қарапайым тізбектерін есептеу әдістері. Тұрақты токты
Электр тізбектерінің пассивтік бөліктерін эквивалентті түрлендіру. Тұрақтытоктың қарапайым тізбектерін есептеу әдістері. Тұрақты токтың күрделі
тізбектерін есептеу әдістері. Кирхгоф заңдарын пайдалану арқылы есептеу
әдісі. Контурлық токтар әдісі. Қуаттар тепе-теңдігі.
Күрделі электр тізбектерін есептегенде және зерттегенде көп жағдайда электр
тізбектері сұлбасын бір түрінен басқа түріне түрлендіру жолдарымен есепті әлдеқайда
жеңілдетуге және көрнекті етіп жасауға болады. Барлық жағдайда берілген сұлбаны
баламалы яғни басқа түрдегі сұлбаға ауыстыру үшін түрлендіруге кірмей қалған сұлба
бөлігіндегі токтар мен кернеулердің өзгермейтін шарттары орындалуға тиісті.
1. Кедергілердің тізбектей жалғануы R1 , R2 , ..., Rn
кедергiлер бірізді
жалғанған кезде олар арқылы бір ғана ток өтеді, сондықтан бір тармақ пайда
болады және оны кедергілердің бірізді жалғануы деп атайды. Кiрердегi кернеу әр
элементтердегi кернеулердiң қосындысына тең. Тiзбектiң баламалы кедергiсi n
кедергiлердiң қосындысына тең
n
Ráàë Rk Ток тең: I U
Ráàë
k 1
Элементтердегi кернеу:
U1 IR1 ,U 2 IR2 ,...,U n IRn
Екi бірізді жалғанған кедергiден тұратын тiзбектегi ток:
Элементтердегi кернеу:
U
U
U1 R1
U1 IR1
R1 , U 2 IR2
R2 ,
.
R1 R2
R1 R2
U 2 R2
I
U
R1 R2
2.
2. Кедергілердің параллель жалғануы. Егер тізбектің екі түйіңі арасында бірнешекедергі параллель жалғанған кезде олардың әрқайсысыңа бірдей кернеу беріледі,
U
U
U
сонда Ом заңы бойынша әр кедергідегі ток:
I1 , I 2 , ...I n
R1
R2
Rn
Кiрер ток элементтердегi токтардың қосындысына тең:
U U1 U 2 ... U n .
I I1 I 2 ... I n
U U
U
...
R1 R2
Rn
1
1
1
1
U
U
...
UGáàë
R
R
R
R
2
n
áàë
1
Мұндағы Gáàë тiзбектiң баламалы өткiзгiштiгi. Параллель жалғанғанда:
n
n
1
1
, Gáàë Gk Екі кедергі параллель жалғанған кезде балама кедергі
Ráàë k 1 Rk
k 1
тең:
Ráàë
R1R2
R1 R2 Тармақталмаған бөлiгiндегi ток:
I
U
Ráàë
3.
3. Кедергілердің аралас жалғануы. Аралас жалғану, ол бірізді және параллельжалғанған кедергілердің тіркестері.
U
Токтар тең болады: I R
áàë
Ráàë. R1
R2 R3
R2 R3
I1 I
R2
R
, I2 I 3
R2 R3
R2 R3
Бiрiздi-параллель жалғанған элементтер үшiн баламалы өткiзгiштiк:
Gáàë. G1 G23 G1
1
.
R2 R3
4. Үшбұрышты жалғанған кедергiлерді жұлдызшаға түрлендiру.
Үшбұрыш түрiнде жалғанған кедергiлердi баламалы жұлдызшаға түрлендiру
формулалары келесі түрге ие:
R12
R1R2
,
R1 R2 R3
R23
R2 R3
,
R1 R2 R3
R13
R1R3
.
R1 R2 R3
4.
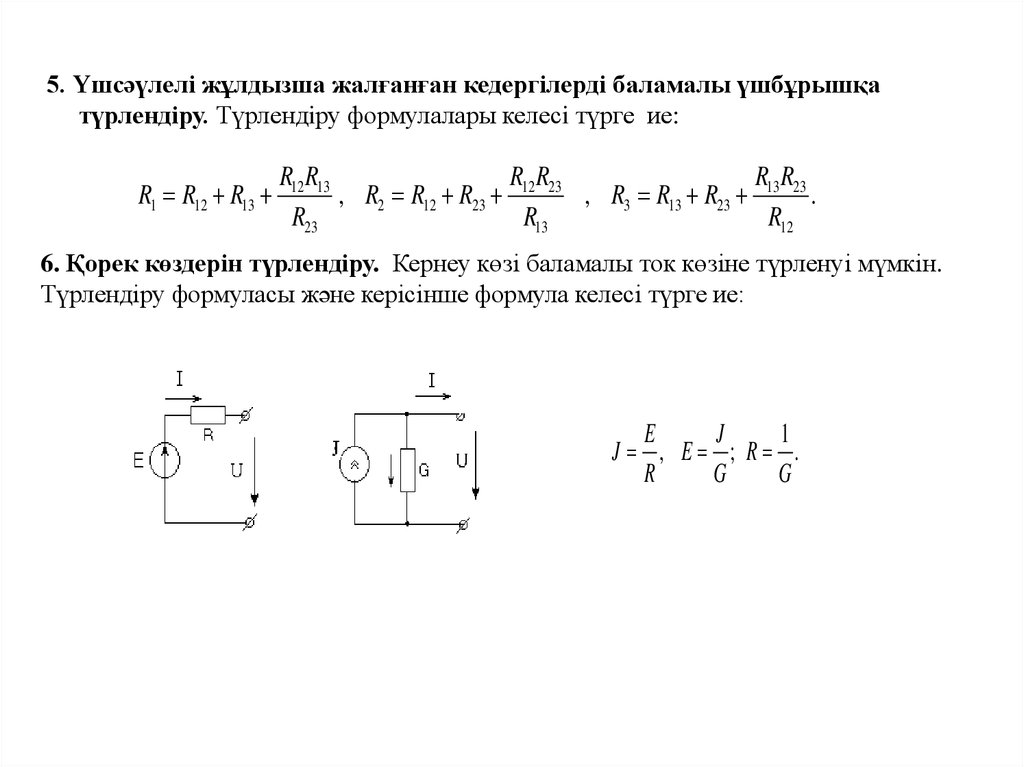
5. Үшсәүлелi жұлдызша жалғанған кедергілерді баламалы үшбұрышқатүрлендiру. Түрлендiру формулалары келесi түрге ие:
R1 R12 R13
R12 R13
R R
R R
, R2 R12 R23 12 23 , R3 R13 R23 13 23 .
R23
R13
R12
6. Қорек көздерiн түрлендiру. Кернеу көзi баламалы ток көзiне түрленуi мүмкiн.
Түрлендiру формуласы және керiсiнше формула келесi түрге ие:
E
J
1
J , E ; R .
R
G
G
5.
7. Қоректендіргіштері бірізді немесе параллель жалғанған тізбекті есептеу үшінбалама түрлендіру тәсілін пайдалануға болады.
а)Қоректендіргіштер бірізді жалғанса, онда оларды бір балама қоректендіргішпен
айырбастауға (түрлендіруге) болады. Балама қоректендіргіштің э.қ.к.-і Eб
қоректендіргіштердің э.қ.к.-терінің алгебралық қосындысына тең, ал ішкі кедергісі
Rб қоректендіргіштердің ішкі кедергілерінің арифметикалық қосындысына тең:
Rб=R1+R2+...+Rn. Бағыттары токтың бағыттымен бағыттас э.қ.к.-тер плюс
таңбасымен алынады. Керісінше жағдайда таңбасы минус болады.
ә) Параллель жалғанған қоректендіргіштерді бір балама қоректендіргішпен
айырбастауға (түрлендіруге) болады . Кирхгофтың бірінші заңы бойынша:
I=I1+I2+I3+I4, немесе
(Eб – Uаб)/Rб =(E1 – Uаб)/R1+(E2 – Uаб)/R2 +(-E3 – Uаб)/R3+(E4 – Uаб)/R4.
Бұдан Eб= (E1G1+ E2G2-E3G3+E4G4 )/(G1+G2+G3+G4 ), 1/Rб=1/R1+1/ R2+1/ R3+1/R4=
G1+G2+G3+G4.
Жалпы жағдайда
Yб= Ei Gi /
Gi
6.
Тұрақты токтың бірнеше э.қ.к-тері бар тармақталған тізбектерін есептеу үшінмынандай тәсілдерді қолдануға болады:
1) Кирхгофтың заңдарын пайдаланып есептеу тәсілі;
2) Контурлық тоқтар тәсілі;
3) Түйіндік потенциалдар тәсілі;
4) Екі түйіндік тәсіл;
5) Балама генератор тәсілі.
Кирхофтың заңдарын пайдалану арқылы есептеу тізбектің тармақтарындағы
анықталуға тиісті токтарға қатысты теңдеулер құрудан басталады. Құрылатын
теңдеулер саны белгісіз токтар санына тең. Кирхгофтың бірінші заңы бойынша
құрылатын теңдеулер саны тізбектегі түйін санынан біреуге кем болады, яғни т-1
тең. Мұндағы т- тізбектегі түйіндер саны. Кирхгофтың екінші заңы бойынша
құрылатын теңдеулер саны жалпы құрылатын теңдеулер саны мен бірінші заңы
бойынша құрылатын теңдеулер санының айырмасына тең, яғни к -( т-1). Мұндағы ктізбектегі тармактар саны. Кирхгофтың екінші заңы бойынша теңдеулер құру кезінде
басқа контурға кірмеген тармағы бар тәуелсіз контурлар үшін құруға тырысқан жөн.
1. Тізбекті Кирхофтың заңдарын пайдалану арқылы есептеуді мынадай ретпен
жүргізгеді:
а) Тармақтардағы токтардың оң бағытын қалауымызша таңдап алып, оны сұлбада
белгілеу қажет;
7.
ә) Кирхгофтың екінші заңы бойынша теңдеулер құру үшін контурды айналу бағытынқалауымызша таңдап аламыз;
б) Э.қ.к.- нің алгебралық қосындысын тапқан кезде контурдағы э.қ.к.-нің бағыты
контурды айналу бағытымен сәйкес келсе онда оның таңбасы «+», ал керісінше
жағдайда «-» болады;
в) Токтың бағыты контурды айналу бағытымен сәйкес келсе, онда кернеудің түсуінің
таңбасы таңбасы «+», ал керісінше жағдайда «-» болады;
г) Құрылған теңдеулер жүйесін белгілі тәсілдер арқылы шешу арқылы тармақтардағы
токтарын табамыз.
Кирхгофтың заңдарын пайдаланып суретте көрсетілген тізбектің тармақтарындағы
токтарды табайық. Ол үшін Кирхгофтың бірінші заңы бойынша үш теңдеу құрамыз:
а) –I1– I6 – I3 =0
б) I1+I2 – I5 =0
в) I6 – I2 – I4 =0
Контурлар үшін Кирхгофтың екінші заңы
бойынша үш теңдеу құрамыз:
1-контур) E1 – E3=I1∙R1+I5∙R5 – I3∙R3
2-контур) –E2+E4= -I2∙R2+I4∙R4 – I5∙R5
3-контур) E3 – E4= –I6∙R6–I4∙R4 + I3∙R3
8. .
Құрылған алты теңдеуден тұратын жүйені өзімізге белгілі әдістер арқылышешеміз де, I1,I2,I3,I4,I5,I6 токтарды табамыз
2. Контурлық тоқтар тәсілі. Бұл тәсілді қолданған кезде электр сұлбасының
тәуелсіз контурында тек өзінің контурлық тогы жүреді деп есептейді.
Контурлық ток деп қарастырылған контурдың барлық тармақтарымен жүреді деп
шартты түрде қабылданған ток. Бұл тәсіл бойынша теңдеулер тек Кирхгофтың
екінші заңы бойынша контурлық токтарға байланысты құрылады. Сондықтан
есептеу жұмысы көп жеңілдейді. Контурлық токтар тәсілінің есептеу жұмысында
қолданылуын суретте көрсетілген тізбектің тармақтарындағы токтарды анықтау
арқылы қарастырайық. Әрбір контур үшін контурлық токтың бағытын өз
қалауымызша, мысалы сағат тілінің жүрісінің бағытымен бағыттас етіп таңдап
аламыз. Екі контурға ортақ тармақпен жүретін контурлық токтар бағыттас болса,
онда олардың қосындысы алынады. Керісінше жағдайда олардың айырмасын
алады. Жалпы жағдайда қарастыралатын тізбек үшін теңдеулер мынадай түрде
жазылады:
• Е11= I11∙R11+ I22∙R 12 + I 33∙ R 13
• Е22= I11∙R21+ I22∙R 22 + I 33∙ R 23
• Е33= I11∙R31+ I22∙R 32 + I 33∙ R 33
9. .
Мұндағы Е11, Е22, Е33- бірінші, екінші және үшінші контурлардың контурлық э.қ.к.тері; R11, R22, R 33- бірінші, екінші және үшінші контурлардың өзіндік кедергілері,R11= R1+R5 +R3; R22= R2+R4+R5; R 33= R6+R4 +R3.
R12=R21- бірінші мен екінші контурларға ортақ тармақтың кедергісі, “минус”
таңбасымен алынады. R13= R31- бірінші мен үшінші контурларға ортақ тармақтың
кедергісі, “минус” таңбасымен алынады. R23= R 32- екінші мен үшінші контурларға
ортақ тармақтың кедергісі, “минус” таңбасымен алынады.
Теңдеулер суретте көрсетілген тізбек үшін былай жазылады:
E1 – E3=I11∙(R1+R5 +R3) – I22∙R5 –I33∙R3
– E2+E4= I22∙ (R2+R4+R5) – I33∙R4 –I11∙R5
E3 – E4=I33∙ (R6+R4 +R3) – I11∙R3– I22∙R4
Әр теңдеудегі жақшаның ішінде кедергілердің қосындысы контурдың өзіндік
кедергісі деп аталады. Теңдеулер жүйесін шешеміз де, I11, I22, I33 контурлық токтарын
табамыз. Онан кейін тармақтардың токтарын (I1 ... I6) контурлық токтар арқылы
табамыз:
I1=I11, I2= –I 22, I3= I33 – I11, I4=I22–I33, I5=I11 – I22, I6= –I33.
10.
Сонымен, бiрiктiрiп шығаратын теңдеулер санының қысқаруымен есепәлдеқайда қарапайым болған (алты теңдеулер жүйесi орнына үш теңдеулер
жүйесiн шешемiз).
Кез келген электр тiзбектерi үшiн келесi теңдiк орындалады:
n
n
E I U
k 1
мұндағы :
k k
k 1
k
Ik
- ток көздерiнiң өндiретiн қуаттар қосындысы;
n
U
k 1
k
Jk
- тiзбектегi тұтынылатын қуаттар қосындысы.
n
I
k 1
J k I k2 Rk
- э.қ.к. көздерiнiң өндiретiн қуаттар қосындысы;
n
E
k 1
k
2
k
Rk
Келтірілген теңдiк, қуаттар тепе-теңдiгiнiң (балансының) матаматикалық жазылу
түрi болып саналады. Энергия көздерінің өндіретін қуаттарының алгебралық
қосындысы, тізбектердегі пайдаланатын қуаттар қосындысына тең.









 Физика
Физика








