Похожие презентации:
Теория переноса излучения в веществе
1. 2. Основные понятия в теории переноса излучения в веществе
Содержание1.
2.
3.
4.
5.
6.
7.
Сечения взаимодействия частиц.
Сечения рассеяния и поглощения энергии.
Тормозная способность вещества.
Закон ослабления нерассеянного излучения.
Полный пробег ускоренных частиц в веществе.
Определения, используемые в теории переноса излучения.
Кинетическое уравнение, его физический смысл и структура.
1
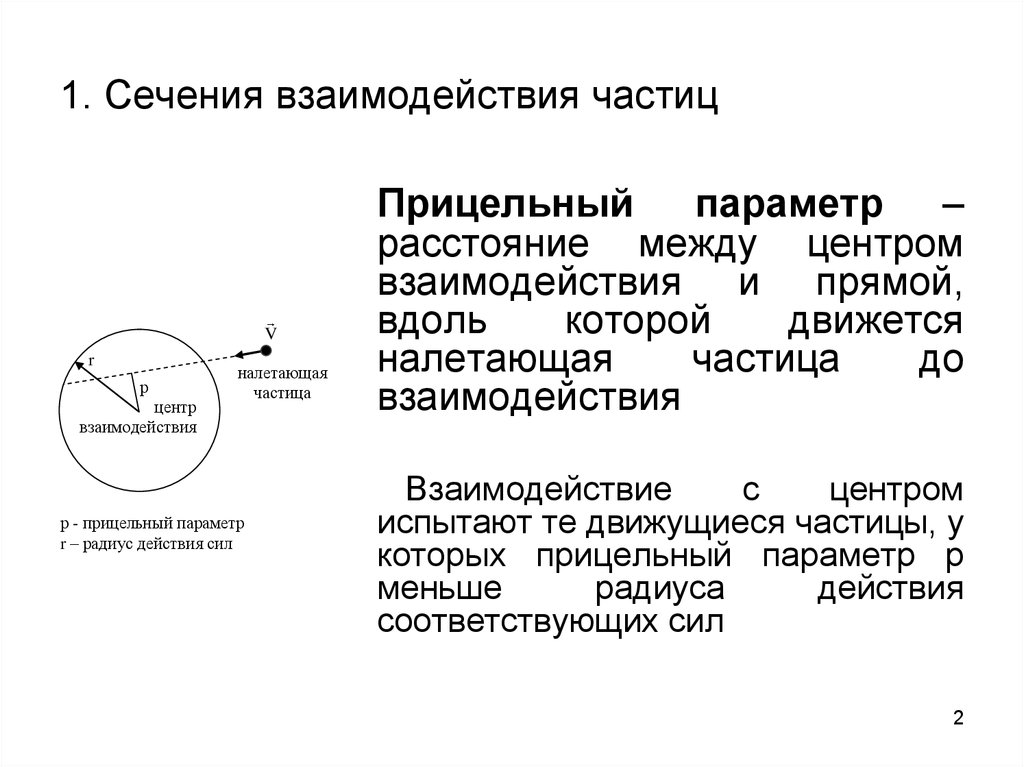
2. 1. Сечения взаимодействия частиц
Vr
р
центр
взаимодействия
налетающая
частица
р - прицельный параметр
r – радиус действия сил
Прицельный
параметр –
расстояние между центром
взаимодействия и прямой,
вдоль
которой
движется
налетающая
частица
до
взаимодействия
Взаимодействие
с
центром
испытают те движущиеся частицы, у
которых прицельный параметр p
меньше
радиуса
действия
соответствующих сил
2
3. 1. Сечения взаимодействия частиц Микроскопическое сечение взаимодействия
• Опр.1.Пусть поток из n частиц (шт./см2) падает на
мишень. N частиц из них испытают взаимодействие с
центром.
Микроскопическим сечением взаимодействия
(т.е. взаимодействия частицы с одним центром)
называется отношение количества частиц N из всего
потока, провзаимодействовавших
с
заданным
центром, к общему количеству частиц, упавших на
мишень:
= N/n.
3
4. 1. Сечения взаимодействия частиц Микроскопическое сечение взаимодействия
Опр. 2. В геометрическом смысле микроскопическоесечение – это площадь круга, центром которого
является центр взаимодействия, попадая в который
движущаяся частица испытает взаимодействие
обязательно
Часто называют
взаимодействия
эффективным
сечением
● В СИ размерность сечения – в м2 или см2. Часто
используют
внесистемную
единицу
барн
(1 барн = 10-24 см2).
4
5. 1. Сечения взаимодействия частиц Микроскопическое сечение взаимодействия
Величина сечения по порядку величины, какправило, равна квадрату радиуса действия сил
между движущимися частицами и центрами
взаимодействия.
Типичные значения эффективных сечений соударения
электронов с атомами газов и паров в диапазоне энергий
102..104 эВ: 10-17..10-15 см2.
Типичные значения рассеяния ионов и возбуждения ими
электронов при энергиях порядка 1..100 кэВ: 10-16..10-17 см2.
Радиус действия сил и сечения взаимодействия
зависят от:
типа
частицы,
являющейся
центром
взаимодействия,
5
- типа и энергии налетающей частицы.
6. 1. Сечения взаимодействия частиц Дифференциальное сечение взаимодействия
• Дифференциальнымпоперечным
сечением
какого-либо процесса, например, рассеяния на
заданный угол , называется коэффициент
пропорциональности между числом частиц N,
испытавших рассеяние в диапазоне углов от до
+d на заданном рассеивающем центре, и числом
частиц n, упавших на единицу поверхности.
d 1 dN( )
d n d
6
7. 1. Сечения взаимодействия частиц Дифференциальное сечение взаимодействия
Дифференциальноесечение
передачи
энергии Т в интервале dT движущейся частицей
частице - центру взаимодействия равно:
d 1 dN (T )
dT n dT
Единицы измерения этого сечения: см2/МэВ.
7
8. 1. Сечения взаимодействия частиц Дифференциальное сечение взаимодействия
• Дифференциальное сечение рассеяниядвижущейся частицы в направлении телесного угла
на величину d равно:
d 1 dN ( )
d n d
Единицы измерения этого сечения: см2/ср.
8
9. 1. Сечения взаимодействия частиц Дифференциальное сечение взаимодействия
• Дваждыдифференциальные
по
направлению
движения и передаваемой энергии микроскопические
сечения:
d
1 dN( , T)
d dT n d dT
9
10. 1. Сечения взаимодействия частиц Дифференциальное сечение взаимодействия
Число частиц NS, которые в результате рассеянияпередадут энергию Т в интервале T и будут лететь
в направлении телесного угла в интервале ,
равно:
d
N s n
T
d dT
10
11. 1. Сечения взаимодействия частиц
Пусть ( E1 , T ) - дифференциальноеT
сечение с передачей энергии T в интервале dT
при начальной энергии E1, тогда полное
сечение рассеяния равно:
(E1 , T)
(E1 )
dT
T
0
Tmax
11
12. 1. Сечения взаимодействия частиц Макроскопическое сечение взаимодействия
• Если j – микроскопическое сечение процесса j, тоwj = Nnuc j
-
вероятность процесса j на единице длины пути
частицы
или
макроскопическое
сечение
взаимодействия типа j.
Nnuc – ядерная плотность вещества.
12
13. 1. Сечения взаимодействия частиц
Полное макроскопическое рассеяние
–
вероятность взаимодействия на единице
длины пути:
w
w j
N nuc j
● Макроскопическое дифференциальное по углам и
энергиям сечение рассеяния
w s (E1 E 2 , 1 2 )
вероятность того, что частица с исходными
параметрами (Е1, 1) на единице длины пути
испытает рассеяния в единичный телесный угол
2 около направления и приобретет энергию в
единичном интервале около значения Е2
-
13
14. 1. Сечения взаимодействия частиц
• Физический смысл полного макроскопическогосечения – среднее число столкновений частицы на
единице длины пути.
• Отсюда следует, что средний пробег частицы между
столкновениями (или длина свободного пробега) :
1 / w( E1 )
14
15. 2. Сечения рассеяния и поглощения энергии
S● Сечение рассеяния частиц:
● Сечение рассеяния энергии: K S
E0
KS
EdN S
0
E 0
E0
число рассеянных частиц
плотность потока падающих частиц
энергия рассеянных частиц
плотность потока падающей энергии
d
dE
1 E 0 d
dE
dE
E
E 0
E 0 0 dE
E
0
- сечение рассеяния с передачей энергии ( E 0 E ),
d - число частиц после рассеяния, рассеянных с
dN S
dE
энергией Е в интервале dE;
- плотность потока падающих частиц;
Здесь
E0 – энергия частиц до рассеяния
15
16. 2. Сечения рассеяния и поглощения энергии
● Сечение поглощения энергии:1
Ka
E0
E0
0
Ka
(E 0 E)
энергия, поглощенная во взаимодействии
плотность потока падающей энергии
d
dE
dE
● Полное сечение рассеяния энергии:
K KS K a
● Дифференциальное сечение для рассеяния энергии
dK dK
,
d dE
показывает, какое количество энергии из всей падающей будет
лететь после рассеяния в направлении Ω или иметь энергию Е
16
17. 3. Тормозная способность вещества
При замедлении в веществе быстрые частицы
теряют свою энергию в результате взаимодействия
с частицами вещества.
Это взаимодействие носит вероятностный
характер и может осуществляться в зависимости от
энергии налетающей частицы и вида участвующих во
взаимодействии частиц.
Пусть E1 – энергия частицы до столкновения,
T – энергия, переданная при одном столкновении,
(E1, T) - макроскопическое сечение передачи энергии в
рассматриваемом
взаимодействии
(среднее
число
столкновений на единице длины пути с потерей энергии Т
в каждом столкновении)
17
18. 3. Тормозная способность вещества
Величина средней
взаимодействии:
1
Tср
(E1 )
энергии,
переданной
при
одном
Tmax
T (E1, T)dT
0
Средняя энергия, потерянная частицей на единице длины
пути в веществе в рассматриваемых столкновениях:
Tср (E1, T)
● Энергия, теряемая частицей на пути ∆R:
E1 Tср R (E1, T) Tср R / (E1 )
18
19. 3.3. Тормозная способность вещества
● Дифференциальные потери энергии можно выразить как:Tmax
E1
dE 1 Tср
d (E1 , T)
N nucl T
dT
R
dR (E1 )
dT
0
Это и есть тормозная способность вещества (линейная
тормозная способность). Она равна средней потерянной
энергии частицы с энергией Е1 на единице пути в веществе во
всех столкновениях, описываемых микроскопическим сечением
σ.
dE
Массовая тормозная способность: 1
dR
19
20. 4. Закон ослабления нерассеянного излучения
Пусть Ф(x) – плотность потока нерассеянных частиц на глубине х,
Ф0 – исходная плотность потока частиц. Тогда:
(x) 0 exp( x)
изменение числа неряссеянных частиц с толщиной вещества (т.е.
среднего количества частиц, не испытавших ни одного
взаимодействия).
Здесь ω – макроскопическое сечение взаимодействия.
● Скорость ослабления числа нерассеянных частиц определяется
величиной ω. Чем больше ω, тем сильнее ослабление пучка
нерассеянных частиц слоями веществ одинаковой толщины.
● ω – линейный коэффициент ослабления (1/см).
-
- массовый коэффициент ослабления (см2/г)
20
21. 4. Закон ослабления нерассеянного излучения
● Вероятность пройти путь х без взаимодействия:(x )
x
P( x )
exp( x ) exp( )
0
21
22. 5. Полный пробег ускоренных частиц в веществе
С увеличением пути, пройденным частицей в веществе,
возрастает потерянная частицей энергия и уменьшается ее
текущая энергия Е.
Пройденный частицей путь R и текущую энергию частицы
можно связать между собой через тормозную способность:
dE
R dR1
0
E dE
dR
R
E1
Если энергия частицы при движении в веществе изменяется
от начальной энергии Е1 до 0, то мы получим полный пробег
частицы с энергией Е1 в веществе:
E1
dE
R1 ( E1 )
0 dE
dR
22
23. 5. Полный пробег ускоренных частиц в веществе
● R1(E1) – средний пробег, так как он вычисляется в соответствиисо средними потерями энергии частицы на единице длины пути.
Средний пробег определяет среднюю длину пути, который
прошла бы частица в процессе замедления в неограниченной и
однородной среде при условии, что она непрерывно теряет
энергию вдоль всего пути в соответствии с тормозной
способностью вещества. Таким образом,
это пробег в
приближении непрерывного замедления.
Пробеги отдельных частиц в веществе носят случайный
характер и распределены возле среднего пробега примерно по
нормальному закону.
23
24. 6. Определения, используемые в теории переноса излучения
(r
● Фазовые координаты , v ) характеризуют
состояние отдельной
частицы в момент времени t (r
- вектор расстояния,
определяющий положение частицы
в пространстве относительно
заданной системы координат, v - вектор скорости). Вместо
скорости часто используют кинетическую энергию частицы
E=mv
2/2 (m – масса частицы) и единичный вектор направления
Элементарный фазовый объем –
dVd dE
, где dV dr dXdYdZ
(r , E , , t )
Дифференциальная плотность частиц
- среднее
число частиц, находящихся в единице фазового объема около
точки ( r , E , , t )
24
25. 2.6. Определения, используемые в теории переноса излучения
Дифференциальная плотность потока
частиц
(r , E , , t )dEd
- число частиц с энергией в
интервале dE около значения Е и
направлением
движения внутри телесного
угла d около направления , пересекающих
в единицу времени единичную площадку с
центром в точке
r и перпендикулярную к
направлению .
25
26. 2.6. Определения, используемые в теории переноса излучения
• Интеграл столкновений-
I (r , E , , t )
число частиц, появившихся в единице фазового объема
около точки ( r , E , ) в единицу времени за счет рассеяния
с изменением параметров: 1 и Е1 Е:
I (r , E , , t )
w( E1 E , 1 )
(r , E1, 1, t )
d 1 dE1
E1 1
2
26
27. 2.7. Кинетическое уравнение, его физический смысл и структура
● это - уравнение баланса частиц в малом объеме в окрестноститочки r
в момент времени t, учитывающее все каналы их
появления и переноса.
В кинетическом уравнении имеем дело
характеристиками поля движения частиц.
со
средними
Рассмотрим малый объем dV около точки r , в котором в
момент времени t находится (r , E , , t )dV частиц с энергией Е
и единичным вектором направления движения . За время t
(r , E, , t t ) dV.
это число изменится и станет равным
Составим уравнение баланса, учитывая
приводящие к такому изменению числа частиц.
процессы,
27
28. 2.7. Кинетическое уравнение, его физический смысл и структура
Увеличение числа частиц
за время Δt в объеме dV с
параметрами Е и может осуществиться в результате
следующих процессов:
1)
прихода частиц в dV за t через поверхность этого объема
dS :
t n Ф( r , E, , t )dS
n 0
2)
прихода частиц в интервале
dV около V за счет процессов
рассеяния (т.е.: E1 E; 1 ).
t d 1 dE1w s ( 1 , E1 E)Ф( r , E1 , 1 , t )dV
3)
рождения частиц за время t: M( r , E, , t )dV
.t
28
29. 2.7. Кинетическое уравнение, его физический смысл и структура
1)
Уменьшение частиц в dV за t происходит в результате:
ухода частиц из dV через поверхность
t nФ( r , E , , t )dS
dS :
n 0
2)
рассеяния частиц с энергией E в объеме dV:
3)
поглощения в объеме dV частиц с энергией Е:
ws ( E )Ф(r , E, , t )dV t
wC ( E )Ф(r , E, , t )dV t
29
30. 2.7. Кинетическое уравнение, его физический смысл и структура
Собирая все члены уравнения вместе, получаем:( r , E, , t t )dV ( r , E, , t )dV t n Ф( r , E, , t )dS
n 0
dV t d 1 dE 1w s ( 1 , E1 E)Ф( r , E1 , 1 , t )
M( r , E, , t )dV t t n Ф( r , E, , t )dS
n 0
w s (E)Ф( r , E, , t )dV t w C (E)Ф( r , E, , t )dV t
30
31. 2.7. Кинетическое уравнение, его физический смысл и структура
Комбинируя члены этого уравнения,деля на dV t при t 0,
учитывая, что: Ф(r , E , , t ) v (r , E , , t ) (v – массовая скорость
движения частиц элемента объема V),
и w(E) = wS(E)+wC(E),
получаем кинетическое уравнение Больцмана для функции
дифференциальной плотности потока движущихся частиц:
1
Ф( r , E, , t ) Ф( r , E, , t ) w (E)Ф( r , E, , t )
v t
d 1 dE1w S ( 1 , E1 E)Ф( r , E, , t) M( r , E, , t)
Примечание. Уравнение Больцмана справедливо только в том случае,
31
когда плотность частиц везде достаточно велика.






























 Физика
Физика








