Похожие презентации:
Прямая в пространстве. (Тема 10)
1.
Кафедра математики и моделированияСтарший преподаватель Г.В. Аверкова
Курс «Высшая математика»
Тема 10 «Прямая в пространстве»
Переход от общих уравнений прямой к каноническому виду,
векторное и параметрические уравнения прямой.
Уравнение прямой, проходящей через две заданные точки.
Угол между двумя прямыми, условие параллельности и
перпендикулярности. Взаимное расположение прямой и
плоскости в пространстве: нахождение точки пересечения
прямой и плоскости, условия параллельности и
перпендикулярности.
2.
Цели и задачиЦели:
– Рассмотреть основные понятия по теме «Прямая в
пространстве»
Задачи:
– Рассмотреть различные способы задания прямой в
пространстве
– Рассмотреть взаимное расположение двух прямых в
пространстве
– Исследовать взаимное расположение прямой и
плоскости
2
3.
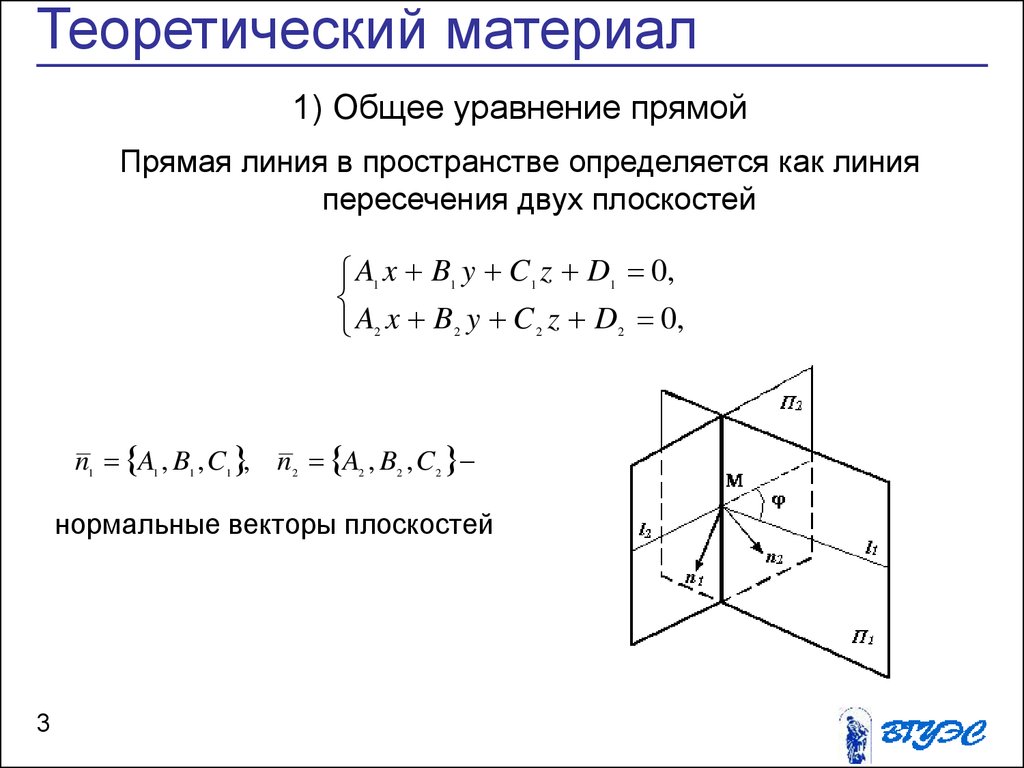
Теоретический материал1) Общее уравнение прямой
Прямая линия в пространстве определяется как линия
пересечения двух плоскостей
A1 x B1 y C1 z D1 0,
A2 x B2 y C 2 z D2 0,
n1 A1 , B1 , C1 , n2 A2 , B2 , C 2
нормальные векторы плоскостей
3
4.
s m, nТеоретический материал
2) Канонические уравнения прямой,
проходящей через заданную точку
параллельно заданному вектору
x x0 y y 0 z z 0
m
n
p
s m, n, p
s n1 n2 ,
4
- направляющий вектор прямой
m
B1 C1
B2 C 2
,
n
A1 C1
A2 C 2
,
p
A1 B1
A2 B2
5.
Теоретический материал3) Уравнение прямой, проходящей через две данные точки
M 1 ( x1 , y1 , z1 ),
M 2 ( x2 , y 2 , z 2 )
x x1
y y1
z z1
x 2 x1 y 2 y1 z 2 z1
4) Параметрические уравнения прямой
x x 0 mt,
y y 0 nt,
z z pt.
0
5
6.
Теоретический материалПараметрические уравнения прямой в векторной форме
r r st 0
6
r
- радиус-вектор точки M ( x, y, z )
r
- радиус-вектор точки M 0 ( x0 , y 0 , z 0 )
7.
Теоретический материалВзаимное расположение прямой и плоскости
x x
y y
z z
,
m
n
p
0
0
Ax By Cz D 0
0
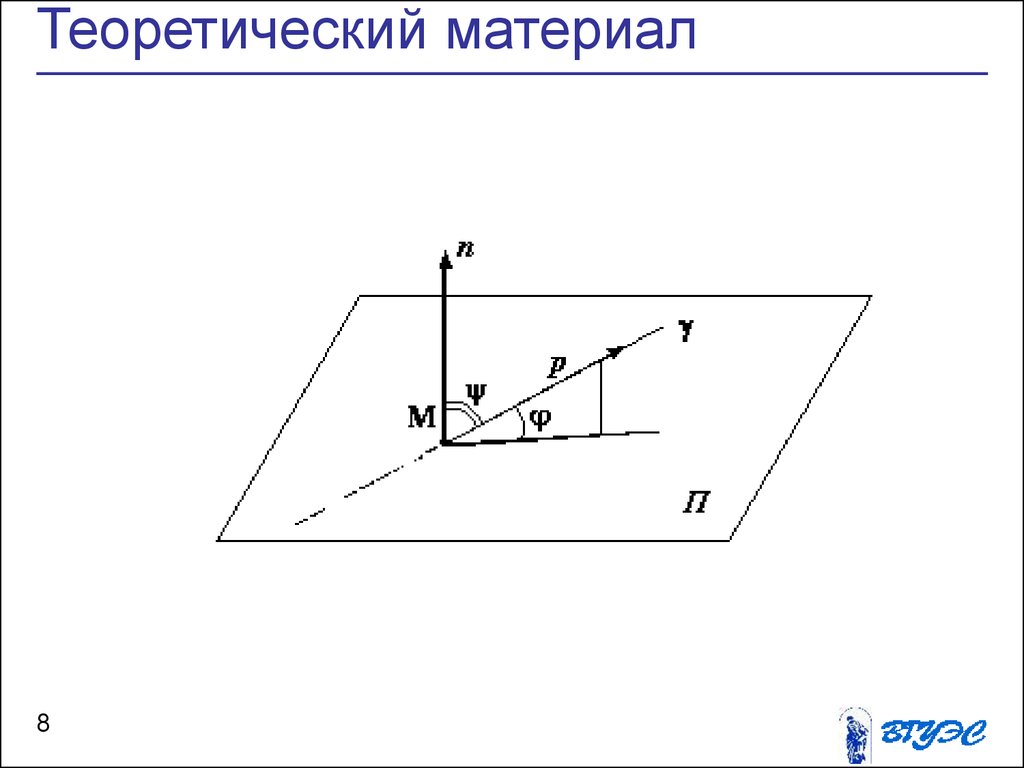
Углом между прямой и плоскостью называется угол между
прямой и ее ортогональной проекцией на плоскость
sin( , l ) cos(n , s )
7
n s
n s
Am Bn Cp
A B C m n p
2
2
2
2
2
2
8.
Теоретический материал8
9.
Теоретический материалВ пространстве возможны три случая взаимного
расположения прямой и плоскости
• Прямая и плоскость пересекаются
Am Bn Cp 0
Координаты точки пересечения находятся по формулам
x x0 mt,
y y nt,
0
z z pt
0
.
подстановкой значения
параметра
t
9
Ax0 By0 Cz 0 D
Am Bn Cp
10.
Теоретический материалУсловие перпендикулярности прямой и плоскости
l s n
A B C
m n p
• Прямая и плоскость параллельны
Am Bn Cp 0,
l
Ax0 By0 Cz 0 D 0
• Прямая принадлежит плоскости
Am Bn Cp 0,
l
Ax0 By0 Cz 0 D 0
10
11.
Теоретический материалВзаимное расположение двух прямых
x x
y y z z
,
m
n
p
1
1
1
1
1
1
x x2 y y2 z z 2
m2
n2
p2
Углом между двумя прямыми в пространстве называется
любой из углов, образованных двумя прямыми, проведенными
через произвольную точку пространства параллельно данным
cos(l1 , l 2 ) cos(s1 , s 2 )
11
s1 s 2
m1 m2 n1 n 2 p1 p 2
s1 s 2
m12 n12 p12 m22 n 22 p 22
12.
Теоретический материалВ пространстве возможны четыре случая взаимного
расположения двух прямых
• Прямые параллельны
l l s s ,
1
2
1
2
M 1 ( x1 , y1 , z1 ) l 2 ,
.
• Прямые совпадают
s1 s 2 M 1 M 2
12
M 2 ( x 2 , y 2 , z 2 ) l1
13.
Теоретический материал• Прямые пересекаются
• Прямые являются скрещивающимися
Две непараллельные прямые пересекаются
при выполнении условия
M M (s s ) 0
1
2
1
2
или
x 2 x1 y 2 y 1 z 2 z 1
m1
n1
p1
m2
n2
p2
0
В противном случае прямые являются скрещивающимися
13
14.
Теоретический материалУсловие перпендикулярности двух прямых
l1 l 2 s1 s 2 m1 m 2 n1 n 2 p1 p 2 0
Расстояние от точки до прямой
d d (M , l )
14
s M 0M
s
15.
Ключевые понятияПрямая
Нормальный вектор
Направляющий вектор
Расстояние от точки до прямой
Угол между двумя прямыми
Параллельность и перпендикулярность
15
16.
Контрольные вопросыОбщее уравнение прямой
Уравнение прямой по двум точкам
Канонические уравнения прямой
Параметрические уравнения прямой
Угол между прямой и плоскостью
Взаимное расположение прямой и плоскости в
пространстве
Угол между двумя прямыми
Взаимное расположение двух прямых в
пространстве
Расстояние от точки до прямой
16
17.
Дополнительная литература17















 Математика
Математика








