Признаки параллелограмма

1. Геометрия 8 класс Признаки параллелограмма (приложения к уроку)

Сокирко Светлана Петровна
учитель математики и физики
МОУ «СОШ №15 п. Березайка»
Бологовского р.
Тверской обл
.
Геометрия 8 класс
Признаки параллелограмма
(приложения к уроку)

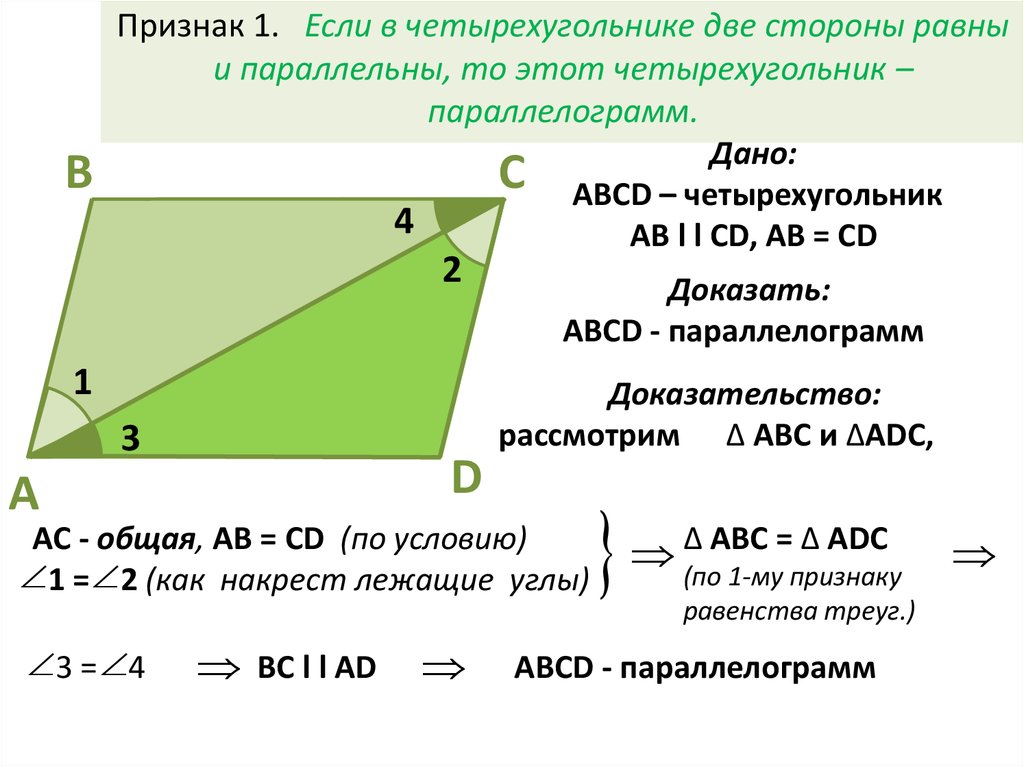
2. Признак 1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.

В
Признак 1. Если в четырехугольнике две стороны равны
и параллельны, то этот четырехугольник –
параллелограмм.
Дано:
С АВСD – четырехугольник
4
AB l l CD, AB = CD
2
1
Доказать:
АВСD - параллелограмм
Доказательство:
рассмотрим ∆ АВС и ∆ADC,
3
D
A
AC - общая, AB = CD (по условию)
1 = 2 (как накрест лежащие углы)
3 = 4
BC l l AD
= ∆ ADC
∆(поАВС
1-му признаку
равенства треуг.)
АВСD - параллелограмм

3. Повторите доказательство теоремы самостоятельно!

В
С
4
2
1
3
A
D

4. Решите задачу. В параллелограмме ABCD точки A₁, B₁, C₁, D₁ - середины отрезков OA, OB, OC, OD

B
C
B₁
A₁
A
O
C₁
D₁
D
Докажите, что четырехугольник A₁B₁C₁D₁ параллелограмм

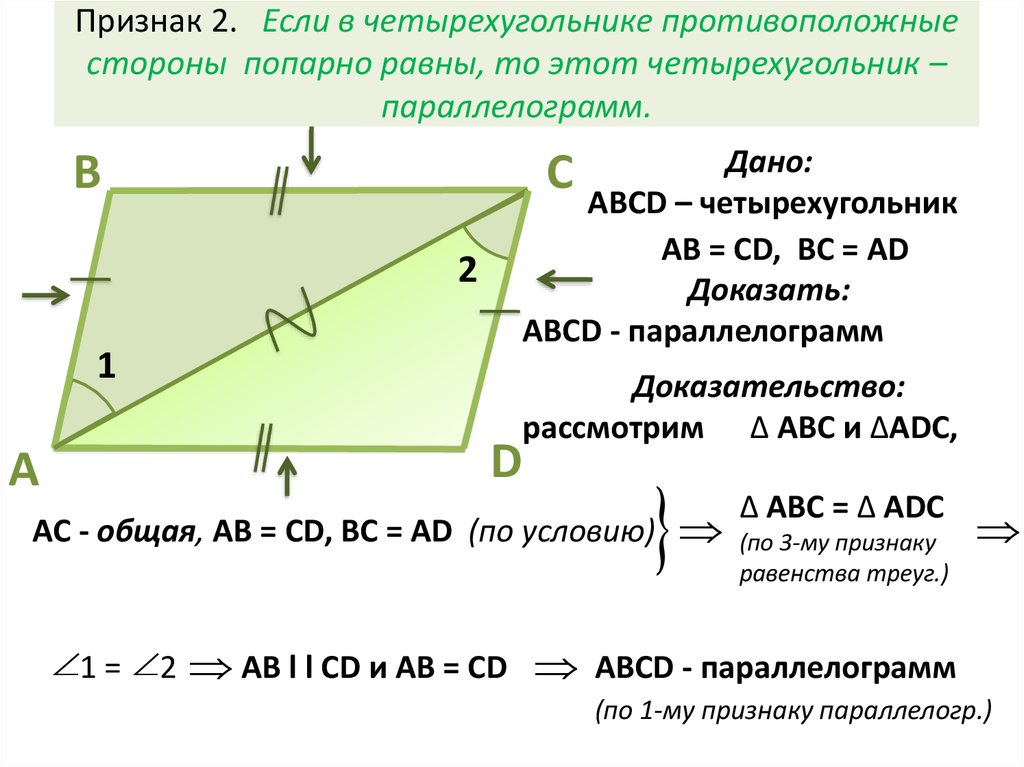
5. Признак 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.

Дано:
С АВСD – четырехугольник
В
2
1
AB = CD, BC = AD
Доказать:
АВСD - параллелограмм
Доказательство:
рассмотрим ∆ АВС и ∆ADC,
D
А
AC - общая, AB = CD, BC = AD (по условию)
1 = 2
∆ АВС = ∆ ADC
(по 3-му признаку
равенства треуг.)
AB l l CD и AB = CD АВСD - параллелограмм
(по 1-му признаку параллелогр.)

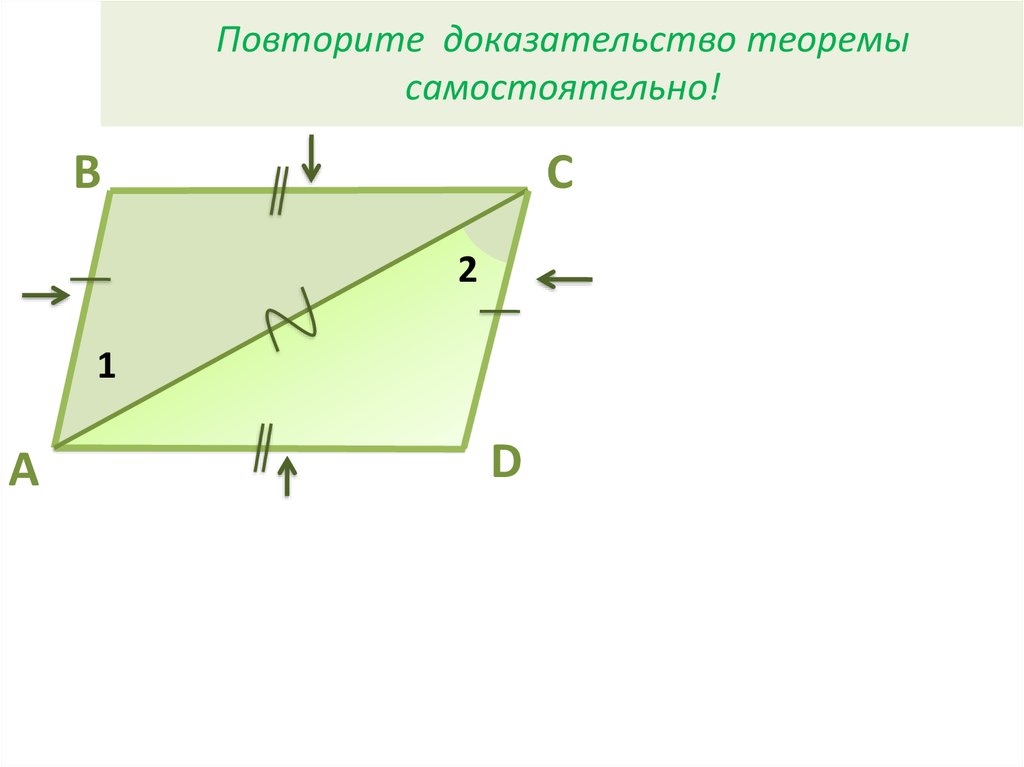
6. Повторите доказательство теоремы самостоятельно!

В
С
2
1
А
D

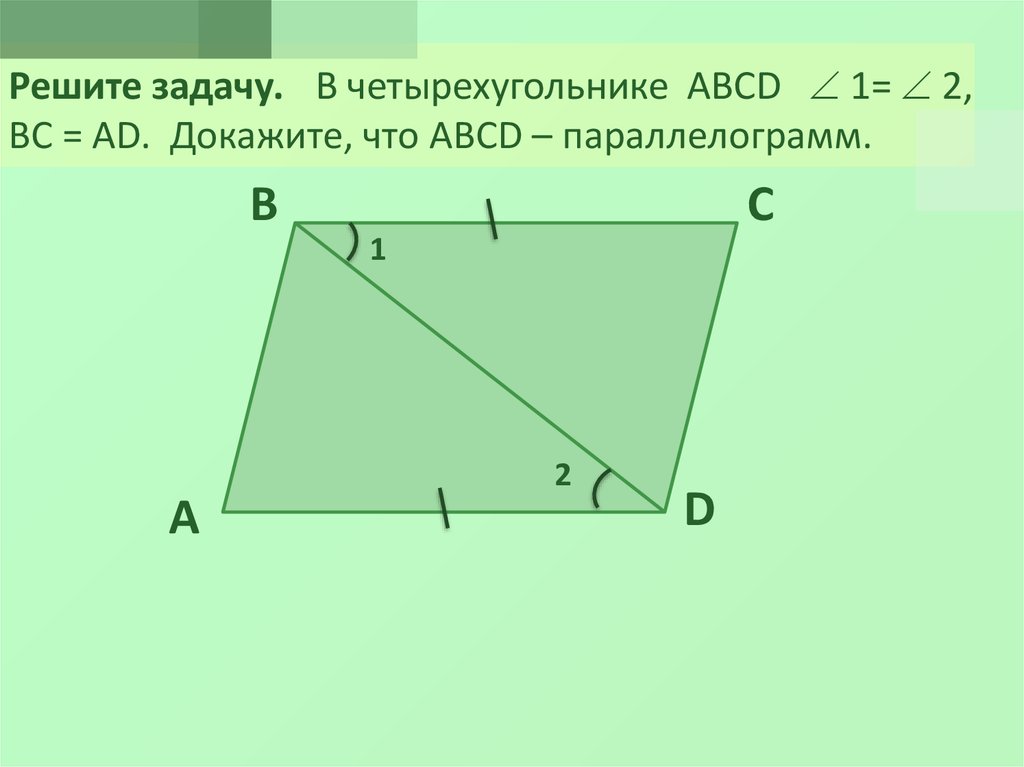
7. Решите задачу. В четырехугольнике ABCD  1=  2, ВС = АD. Докажите, что ABCD – параллелограмм.

Решите задачу. В четырехугольнике ABCD 1= 2,
ВС = АD. Докажите, что ABCD – параллелограмм.
B
C
1
2
A
D

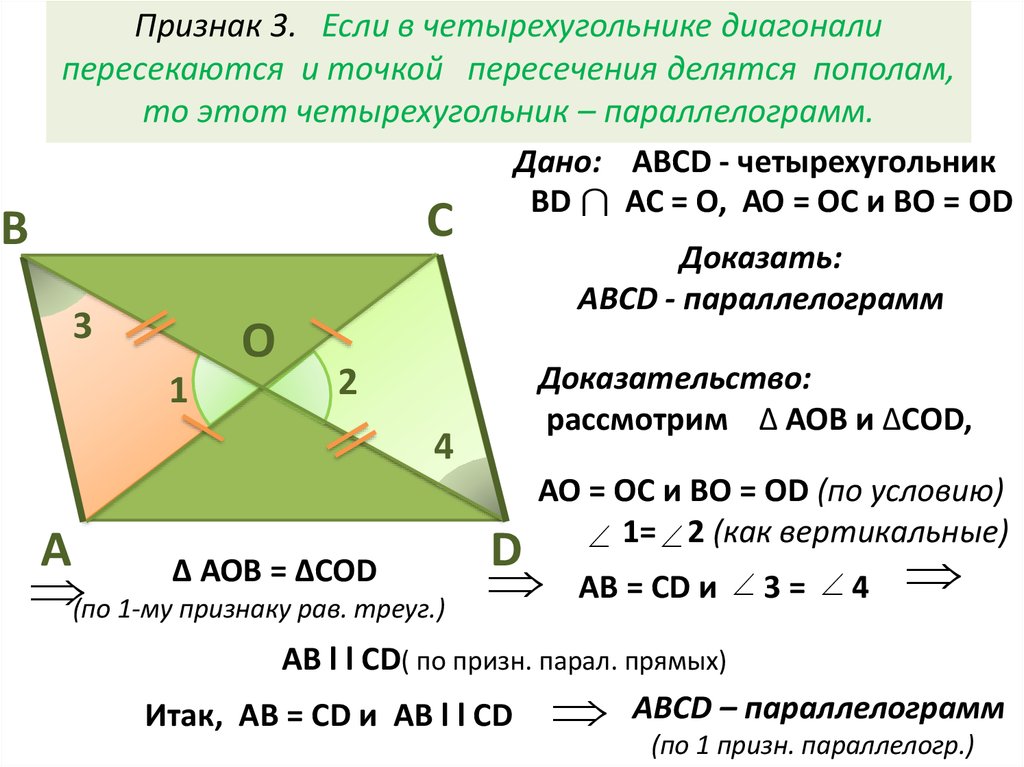
8. Признак 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

В
Признак 3. Если в четырехугольнике диагонали
пересекаются и точкой пересечения делятся пополам,
то этот четырехугольник – параллелограмм.
Дано: АВСD - четырехугольник
ВD AC = O, АО = ОС и ВО = ОD
С
3
O
1
Доказать:
ABCD - параллелограмм
Доказательство:
рассмотрим ∆ АОВ и ∆СОD,
2
4
А
D
АО = ОС и ВО = ОD (по условию)
1= 2 (как вертикальные)
(по 1-му признаку рав. треуг.)
∆ АОВ = ∆СОD
АВ = СD и 3 = 4
АВ l l СD( по призн. парал. прямых)
Итак, АВ = СD и АВ l l СD ABCD – параллелограмм
(по 1 призн. параллелогр.)

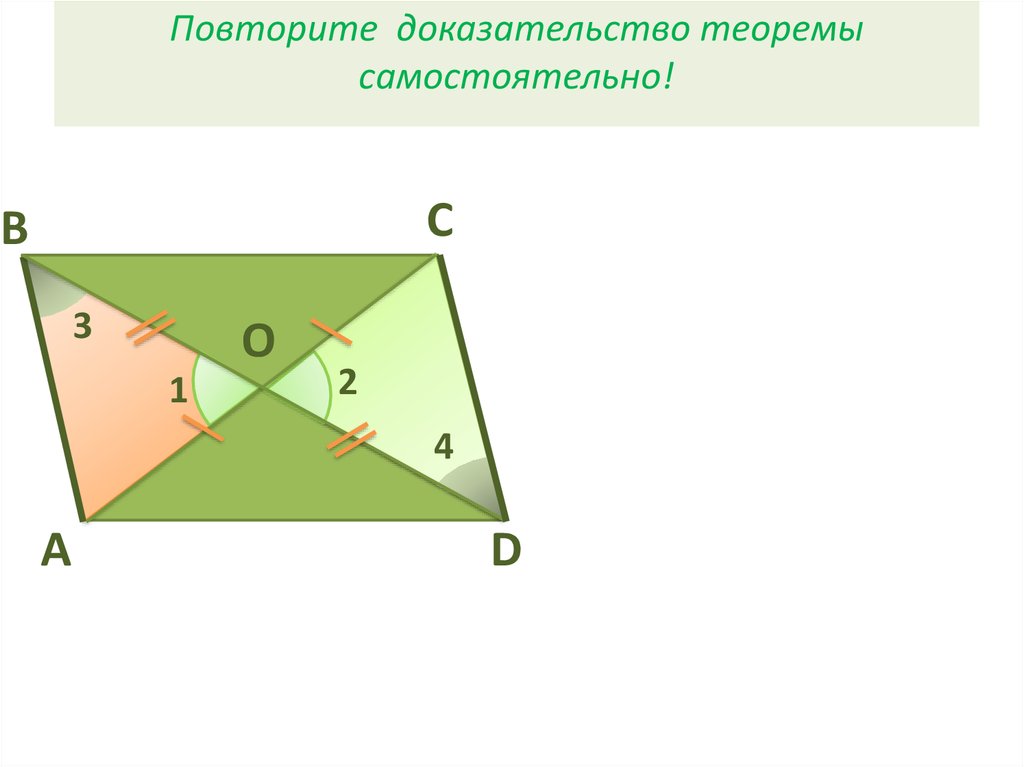
9. Повторите доказательство теоремы самостоятельно!

С
В
3
O
1
2
4
А
D

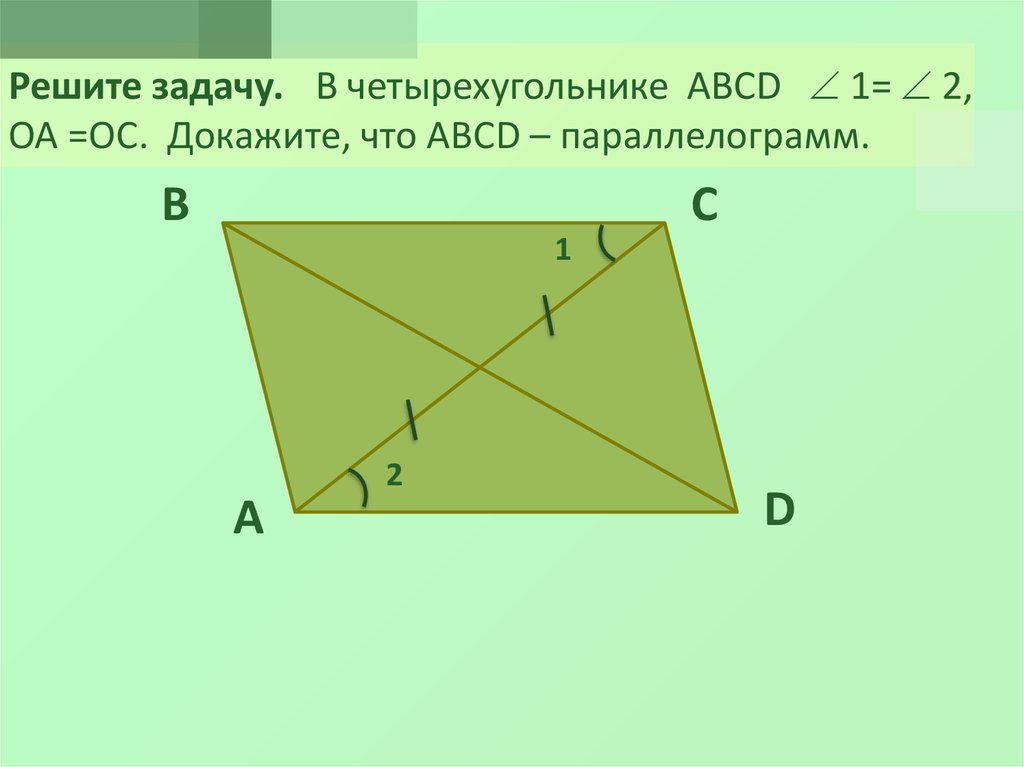
10. Решите задачу. В четырехугольнике ABCD  1=  2, ОА =ОС. Докажите, что ABCD – параллелограмм.

Решите задачу. В четырехугольнике ABCD 1= 2,
ОА =ОС. Докажите, что ABCD – параллелограмм.
B
C
1
2
A
D

11. Литература

Л. С. Атанасян, В. Ф. Бутузов и др.
Геометрия 7-9
Н. Ф. Гаврилова. Поурочные разработки по
геометрии: 8 класс. M.: ВАКО, 2004. – 288с.
– (В помощь школьному учителю)
Мельникова Н. Б., Лепихова М.
Тематический контроль по геометрии. 8 кл.
- М.: Интеллект-Центр. 2007.