Математическая логика. (Тема 2)

1. Математическая логика

Тема 2

2. Основные понятия

• Логика – это наука о способах доказательства
• Математическая логика представляет собой формальный
математический аппарат, изучающий различные способы
доказательства логических рассуждений
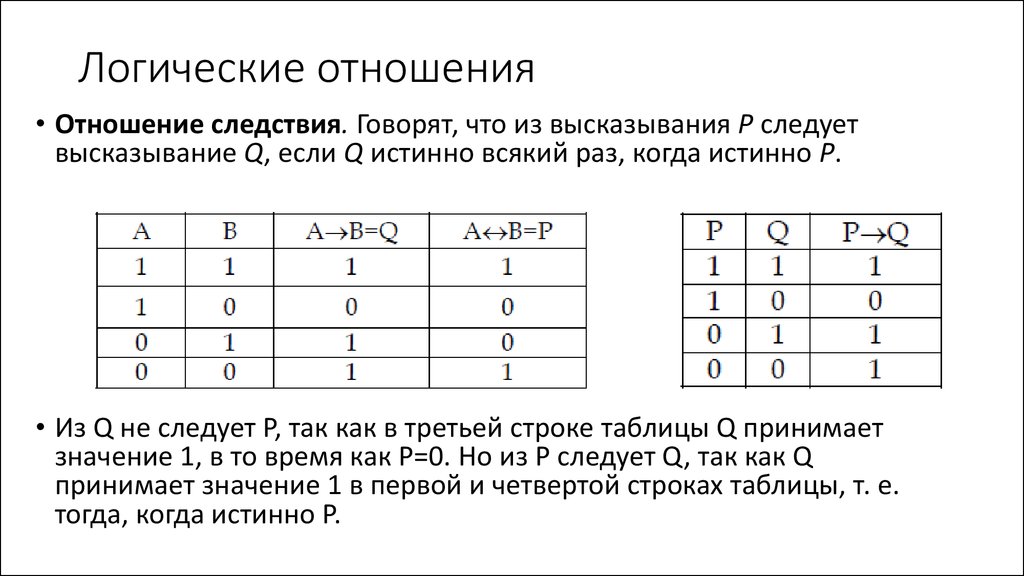
• Высказывание – предложение, относительно которого можно
утверждать, истинно оно или ложно.
• Простейшую из формальных логических теорий называют
алгеброй высказываний.
• Любое логическое рассуждение состоит из высказываний
• Будем обозначать элементарные высказывания латинскими
буквами A, B, C, ... , X, Y, Z ...

3. Основные понятия

• Если высказывание истинно (ложно) в любой логической
ситуации, то оно называется тождественно истинным (ложным),
или логической константой, обозначаемой соответственно И(Л).
Высказывания, истинные в одних логических ситуациях и ложные
в других, называются переменными высказываниями.
• Высказыванию, истинному во всех логически возможных случаях,
т.е. логической константе, обозначаемой 1 или И, будет
соответствовать универсальное множество.
• Высказыванию, ложному во всех логически возможных случаях,
т.е. логической константе, обозначаемой 0 или Л, будет
соответствовать пустое множество.
• Операции алгебры высказываний образуют Булеву алгебру.

4. Логические операции

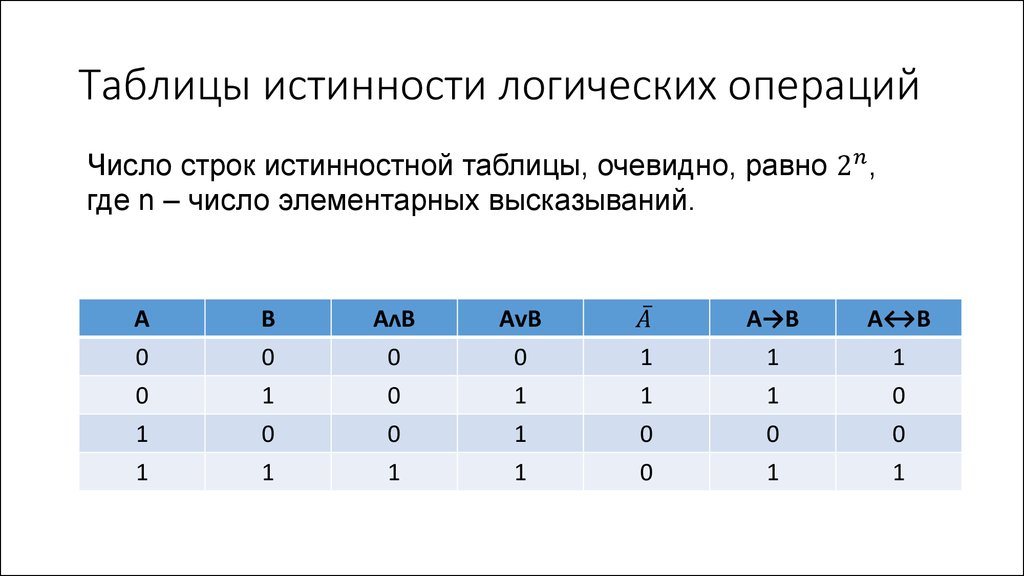
• Конъюнкция двух элементарных высказываний истинна тогда и
только тогда, когда оба элементарных высказывания истинны.
Обозначается AᴧB, A&B, AB. Читается: «A и B».
• Дизъюнкция двух элементарных высказываний является ложным
высказыванием тогда и только тогда, когда оба высказывания, ее
составляющие, ложны. Обозначается АᴠВ. Читается: «А или В».
Разделительный смысл союза «или» исключается.
• Отрицание. Единственная логическая операция, относящаяся к
одному высказыванию, – унарная, в отличие от остальных –
бинарных. Обозначается: