Физические основы механики. Кинематика

1.

2. Основная задача кинематики

Математически описать движение
Описать движение –указать положение тела в каждый момент
времени
Таблица
t, c
x, м
0
0
1
2
2
4
4
8
График
x
Уравнение
t
x t xt

3.

-линия, описываемая движущейся точкой в пространстве
S - сумма длин всех
участков траектории, пройденных точкой за промежуток времени от t0 до t.
– векторная
r
величина, равная вектору, проведенному из начальной точки траектории
тела в конечную точку и измеряемому
длиной отрезка прямой между
начальной и конечной точками
При движении по произвольной
замкнутой траектории r 0
– скалярная величина,
принимающая только
неотрицательные значения
S t 0

4.

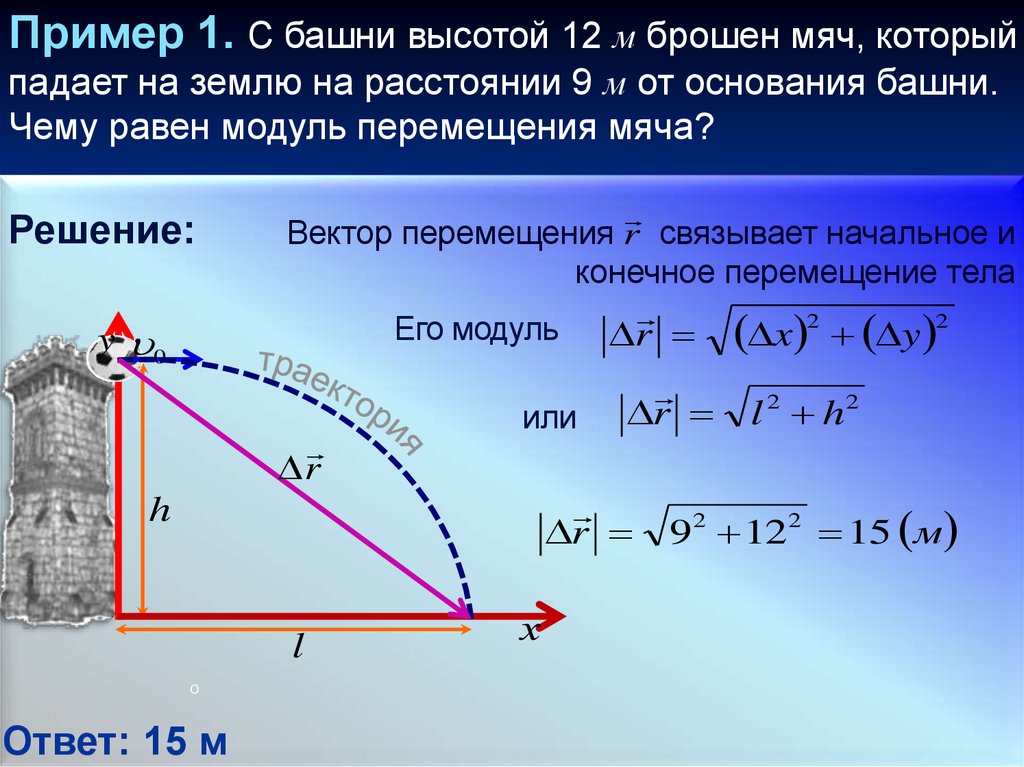
Пример 1. С башни высотой 12 м брошен мяч, который
падает на землю на расстоянии 9 м от основания башни.
Чему равен модуль перемещения мяча?
Решение:
Вектор перемещения r связывает начальное и
конечное перемещение тела
Его модуль
y 0
r
или
r
r
r
h
l
О
Ответ: 15 м
х
x 2 y 2
l 2 h2
92 122 15 м

5.

Пример 2. Велосипедист движется по траектории в
форме окружности радиуса R. За какой-то промежуток
времени он проехал половину длины окружности. Найти
модуль вектора перемещения и путь.
1) r 2R, s 2R 2) r R, s R 3) r 0, s R 4) r 2R, s R
Решение: модуль
вектора перемещения равен диаметру
окружности r 2 R,
а путь - половине длины окружности
s R
R
Ответ: 4

6.

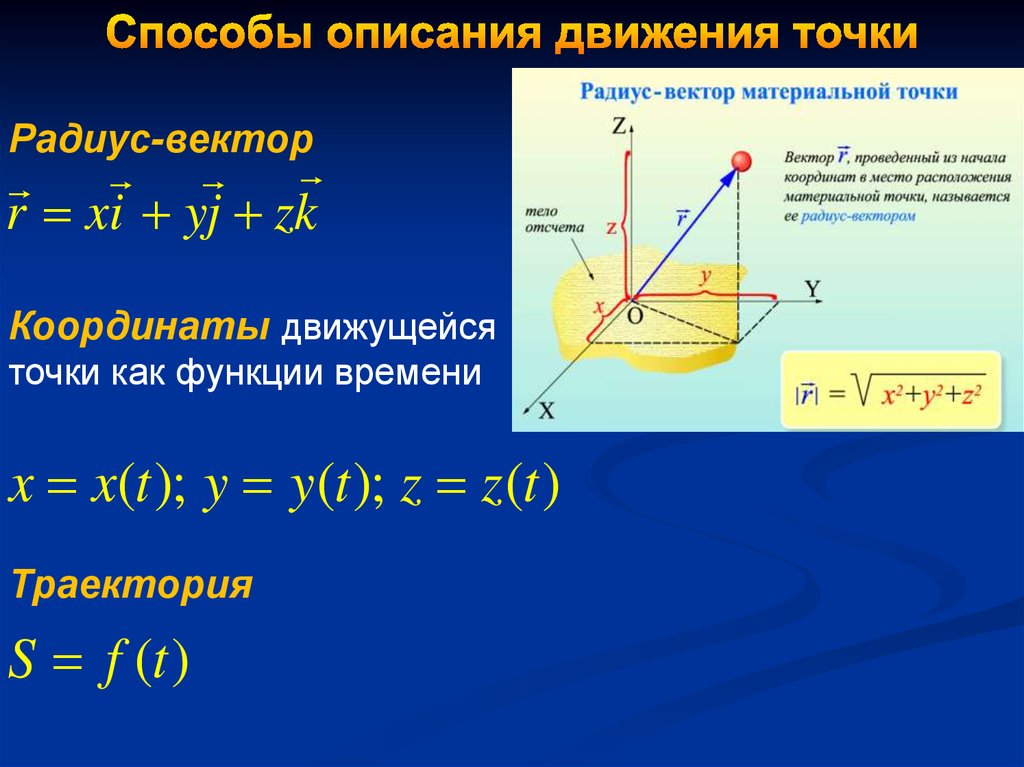
Радиус-вектор
r xi yj zk
Координаты движущейся
точки как функции времени
x x(t ); y y(t ); z z (t )
Траектория
S f (t )

7.

:
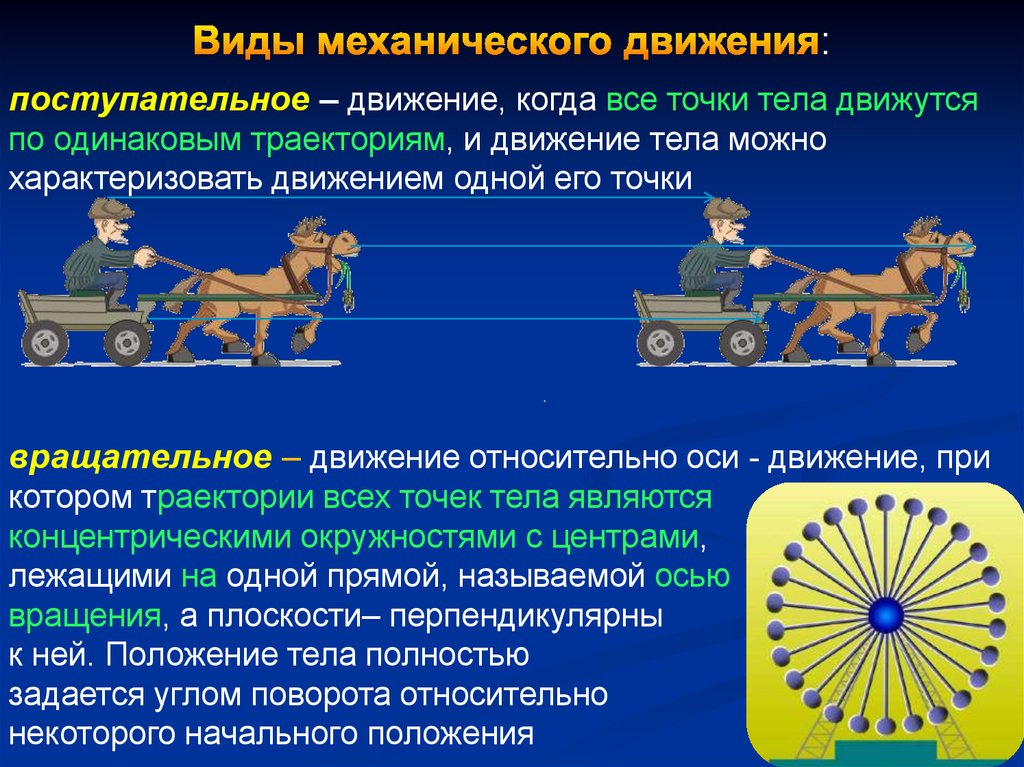
поступательное – движение, когда все точки тела движутся
по одинаковым траекториям, и движение тела можно
характеризовать движением одной его точки
.
вращательное – движение относительно оси - движение, при
котором траектории всех точек тела являются
концентрическими окружностями с центрами,
лежащими на одной прямой, называемой осью
вращения, а плоскости– перпендикулярны
к ней. Положение тела полностью
задается углом поворота относительно
некоторого начального положения

8.

9.

Скорость – величина, показывающая быстроту и направление движения тела
Средняя скорость – скалярная величина, равная отношению длины
пути, пройденного за промежуток времени Δt, к длительности этого
промежутка времени Δt: :
s
t или
r
t
Мгновенная скорость (скорость в данный момент времени) векторная величина, равная первой производной по времени от радиусвектора движущейся точки: численно равна первой производной от
перемещения по времени:
ds
dr
или r
dt
dt
dr dx dy dz
i
j k
dt dt
dt
dt
Абсолютное значение мгновенной скорости:
2
2
dx dy dz
dt dt dt
2

10.

Для радиус-вектора
Для траектории
Если известно значение вектора скорости, то по формуле
ds
dr
dt
dt
найдем элементарное перемещение точки
ds dt
dr dt
Интегрируя правую и левую части равенства, получим:
r dt
s dt
В общем случае скорость является функцией времени и
полученную формулу следует записывать таким образом:
r t dt t C
s t dt t C
r r0 при t 0
s s0 при t 0
Постоянная интегрирования С определяется из условия
r r0 0t
s s0 0t

11.

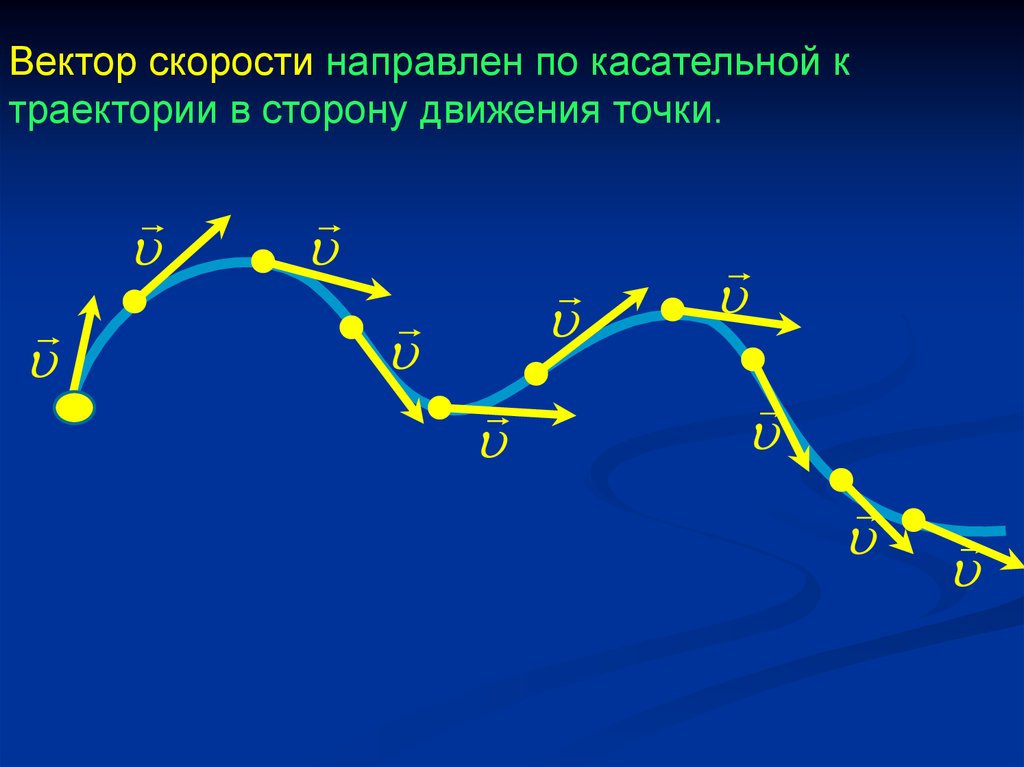
Вектор скорости направлен по касательной к
траектории в сторону движения точки.

12. Сложение скоростей Относительная скорость равна:

Относительная скорость равна:
А) движение в одну сторону
21
2
1
1
21
12 1 2
0
x
2
Б) движение
в противоположные стороны
21 2 1
12 1 2
1
21
0
2
x
В) перпендикулярно
2 21
1
2
2
21 12 1 2

13.

Пример 3. Пассажир поезда, идущего со скоростью
15 м/c, видит в окне встречный поезд длиной 150 м в
течение 6 с, если скорость встречного поезда равна
Решение:
S
t
S
1 2
t
S
1 2
t
150
м
1
15 10 .
6
с
Ответ: 10 м/с

14.

Пример 4. Вертолет удаляется от аэродрома с постоянной
скоростью 16 м/с на север. С какой скоростью начнет
двигаться вертолет относительно аэродрома, если подует
восточный ветер со скоростью 12 м/с?
Решение:

15.

Пример 4. Вертолет удаляется от аэродрома с постоянной
скоростью 16 м/с на север. С какой скоростью начнет
двигаться вертолет относительно аэродрома, если подует
восточный ветер со скоростью 12 м/с?
Решение:
с2 в2 162 122 256 144 400 20 м / с
с
в
Ответ: 20 м/с

16.

Пример 5. Скорость течения реки 0,7 м/с. Скорость лодки
в стоячей воде 1,0 м/с. Под каким углом к берегу нужно
направить лодку, чтобы ее не сносило вниз по течению?
Решение:
в 0,7
cos
0,7, arccos 0,7 46
л
1
Ответ:
460
в
л

17.

Пример 6. Координата тела меняется cо временем по
закону х=8+2t+t2, где все величины выражены в СИ. В
какой момент времени скорость равна 6 м/с?
Решение:
Скорость есть первая производная от координаты
x 2 2t
6 м с
6 2 2t
В момент времени
Ответ: 2 с
t 2c

18.

Пример 7. Координата тела меняется cо временем
согласно формуле х=5-3t+2t2-t3, где все величины
выражены в СИ. Чему равно ускорение тела через 5 с
после начала движения?
Решение:
Ускорение есть первая производная от скорости, а скорость –
первая производная от координаты
x 3 4t 3t 2 м / с
a 4 6t м / с 2
В момент времени t=5 с ускорение
a 4 6 5 26 м / с
Ответ: -26 м/с2
2

19.

Ускорение – величина, показывающая быстроту и направление
изменения скорости тела
Среднее ускорение – скалярная величина, равная отношению
приращения скорости тела за промежуток времени от t до t+Δt, к
длительности этого промежутка времени Δt:
a
t
Мгновенное ускорение - векторная величина, равная первой
производной по времени от скорости движущейся точки:
d d r d 2 x d 2 y d 2 z
a
2 2 i 2 j 2 k ax i a y j az k
dt dt
dt
dt 2 dt
d d s
2
a
dt
dt 2
Абсолютное значение мгновенного ускорения:
2
2
2
d x d y d z
a 2 2 2 a x2 a y2 a z2
dt dt dt
2
2
2

20.

Если известно значение вектора ускорения, то по формуле
получим:
аdt
d
а
dt
В общем случае ускорение является функцией времени и полученную
формулу следует записывать таким образом:
а t dt
a t dt at C
Постоянная интегрирования определяется из условия
0 at
0 при t 0
at 2
S dt 0 at dt 0t
C
2
Постоянная интегрирования определяется из условия s s0 при t 0
at 2
s s0 0 t
2

21.

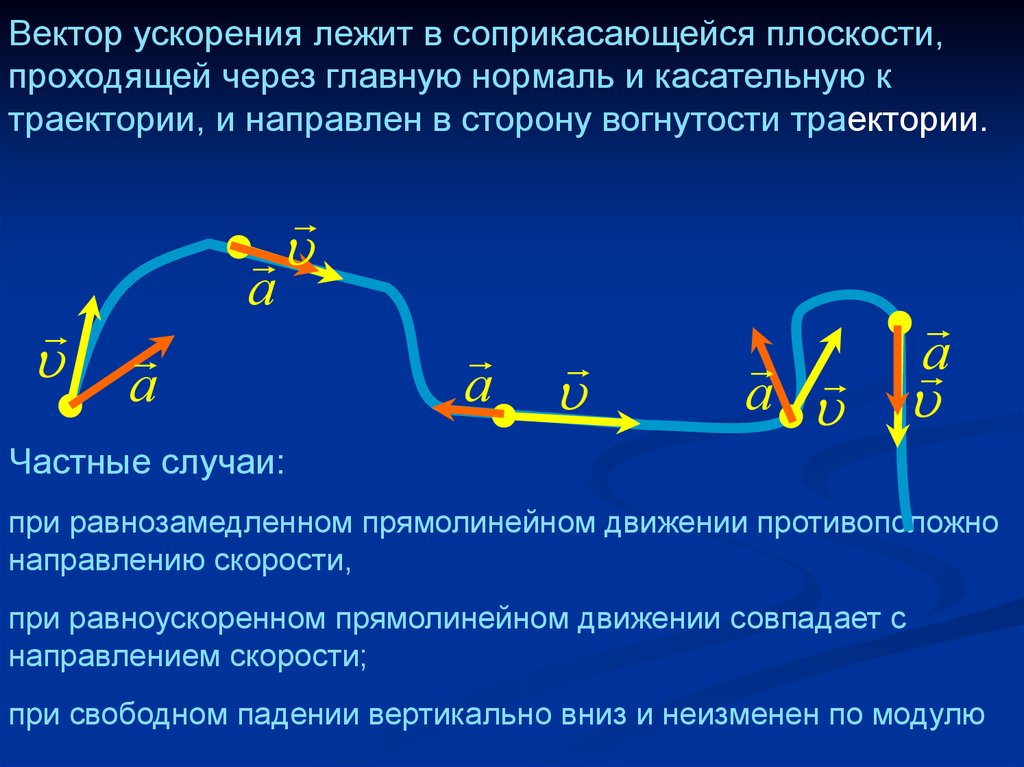
Вектор ускорения лежит в соприкасающейся плоскости,
проходящей через главную нормаль и касательную к
траектории, и направлен в сторону вогнутости траектории.
а
а
а
а
а
Частные случаи:
при равнозамедленном прямолинейном движении противоположно
направлению скорости,
при равноускоренном прямолинейном движении совпадает с
направлением скорости;
при свободном падении вертикально вниз и неизменен по модулю

22.

Т.к. при движении по некоторой траектории в плоскости есть
два направления - касательной к траектории и нормали, то
для нахождения мгновенного ускорения его удобно разложить
на две взаимно перпендикулярные составляющие
Тангенциальное ускорение
а
а
аn
характеризует быстроту изменения
скорости по величине, направлено вдоль
касательной к траектории
d d S
a
2
dt
dt
2
Нормальное ускорение
характеризует быстроту изменения скорости по направлению,
направлено вдоль главной нормали (к центру кривизны траектории)
an
2
r

23.

Если an 0, a 0 , то движение
прямолинейное, равномерное, а =0
Если an 0, a 0, то движение
прямолинейное, неравномерное, а = aτ
Если an 0, a 0, то движение
криволинейное, равномерное, а = an
Если an
0, a 0, то движение
криволинейное, неравномерное,
a a a
2
n
2

24.

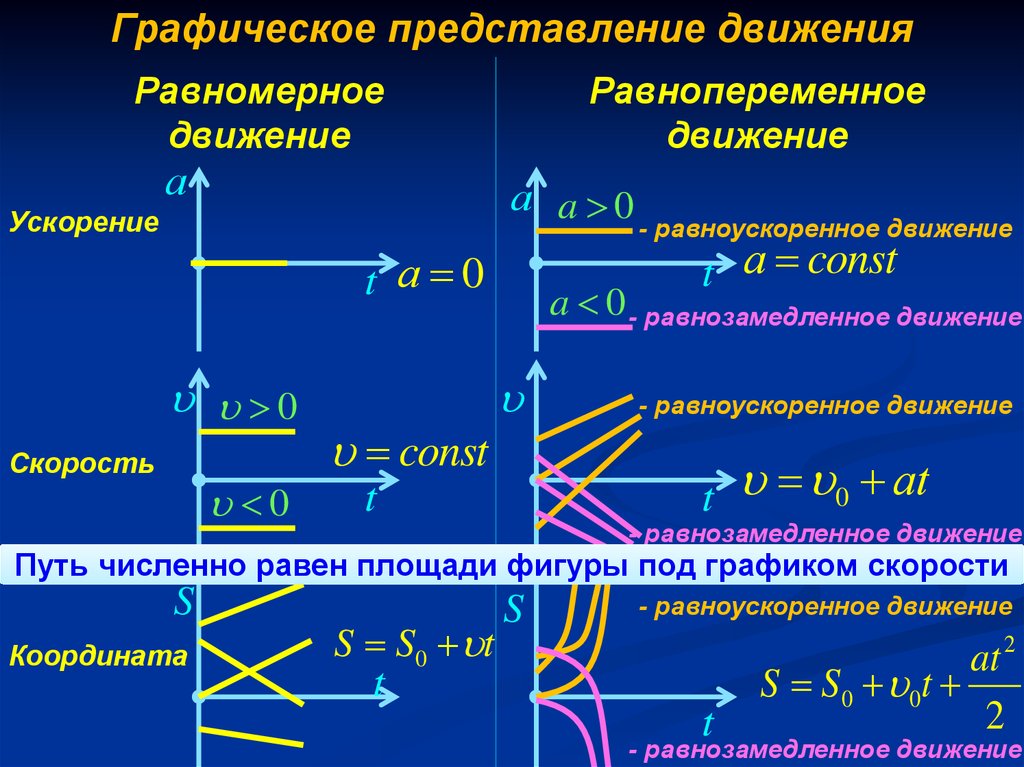
Графическое представление движения
Равномерное
движение
а
Равнопеременное
движение
а a 0
- равноускоренное движение
Ускорение
t а const
t а 0
0
Скорость
0
const
a 0 - равнозамедленное движение
- равноускоренное движение
t 0 аt
t
- равнозамедленное движение
Путь численно равен площади фигуры под графиком скорости
S
Координата
S S0 t
t
S
- равноускоренное движение
t
at 2
S S 0 0t
2
- равнозамедленное движение

25.

Пример 8. В некоторый момент времени вектор скорости и вектор ускорения материальной точки направлены друг относительно друга так, как показано на рисунке.
Такое движение
1) прямолинейное и замедленное;
2) прямолинейное и ускоренное;
3) криволинейное и замедленное;
4) криволинейное и ускоренное.
а
Ответ: 2

26.

Пример 9. В некоторый момент времени вектор скорости и вектор ускорения материальной точки направлены друг относительно друга так, как показано на рисунке.
Такое движение
1) прямолинейное и замедленное;
2) прямолинейное и ускоренное;
3) криволинейное и замедленное;
4) криволинейное и ускоренное.
а
Ответ: 1

27.

Пример 10. В некоторый момент времени вектор скорости и вектор ускорения материальной точки направлены друг относительно друга так, как показано на рисунке.
Такое движение
1) прямолинейное и замедленное;
2) прямолинейное и ускоренное;
3) криволинейное и замедленное;
4) криволинейное и ускоренное.
а
Ответ: 3

28.

Пример 11. В некоторый момент времени вектор скорости и вектор ускорения материальной точки направлены друг относительно друга так, как показано на рисунке.
Такое движение
1) прямолинейное и замедленное;
2) прямолинейное и ускоренное;
3) криволинейное и замедленное;
4) криволинейное и ускоренное.
а
Ответ: 4

29.

Пример 12. Координата тела меняется cо временем
по закону х=8+2t+t2, где все величины выражены в СИ.
Чему равно ускорение тела через 2 с после начала
движения?
Решение:
Ускорение есть вторая производная от координаты и первая
производная от скорости а x 2 м с 2
Ответ: 1

30.

Пример 13. Опишите каждый
а
из видов движения,
представленных на рисунке
0
Ответ:
А- равнозамедленное
Б- ускоренное
В- равноускоренное
Г- равномерное
Б
В
Г
t
А

31.

Пример 14. В каком из
S, м/с
случаев скорость больше?
0
Б
В
Г
А
t, с
Решение: движение равномерное
S t
скорость больше там, где больше угол наклона
Ответ: А

32.

Пример 15. В каком из
ʋ, м/с
случаев ускорение больше?
0
Решение:
наклона
Ответ: В
Б
В
Г
А t, с
at - ускорение больше там, где больше угол

33.

Пример 16. На рис. представлен график зависимости скорости автомобиля от времени.
Найдите путь, пройденный
автомобилем за 4 с.
ʋ, м /c
10
5
0 1 2 3 4 5 t, с
Решение: путь, пройденный автомобилем, численно
равен площади фигуры, ограниченной графиком скорости.
S t 10 4 40 м
Ответ: 40 м

34.

Пример 17. Зависимость пути от времени для
прямолинейно движущегося тела имеет вид
S 2t 3t 3t
2
3
где все величины выражены в СИ. Ускорение тела равно
Решение: зависимость пути от времени при
равноускоренном движении определяется формулой
d d 2 s
a
2
dt dt
2 6t 9t 2 , м с
a 6 18t , м с 2

35.

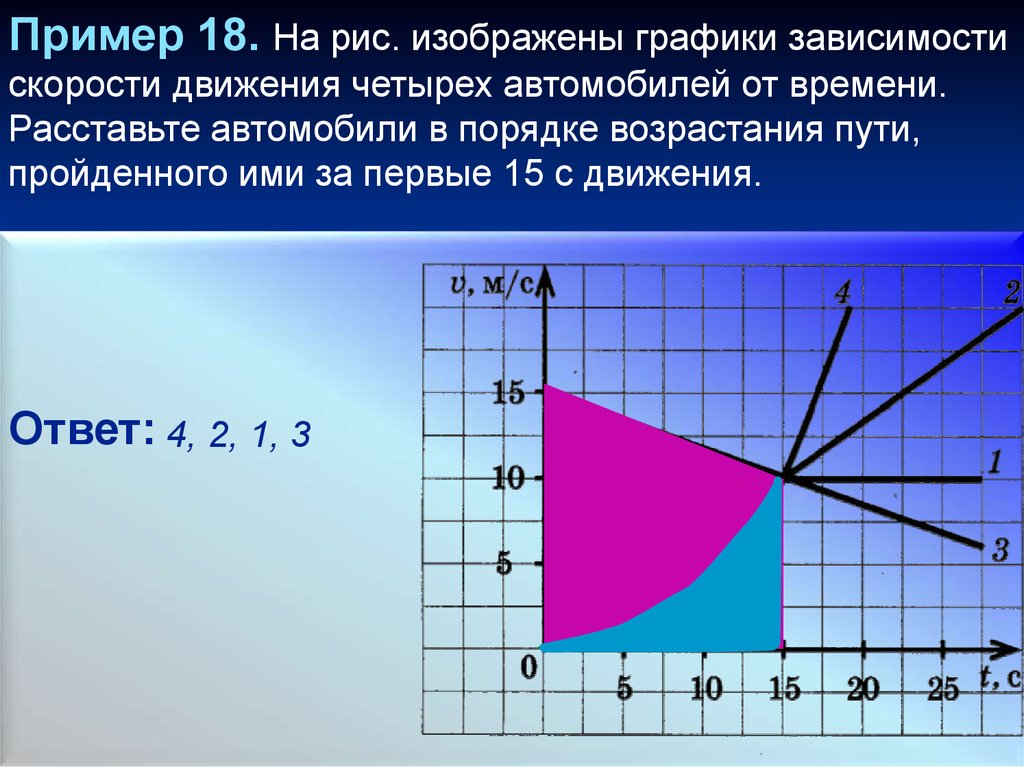
Пример 18. На рис. изображены графики зависимости
скорости движения четырех автомобилей от времени.
Расставьте автомобили в порядке возрастания пути,
пройденного ими за первые 15 с движения.
Ответ: 4, 2, 1, 3

36.

Пример 19. Уравнение движения точки по прямой имеет
2
3
м . Найти:
x
t
2
t
4
t
0
,
2
t
вид
1) среднюю скорость за промежуток времени от t1=4c до t2=6c
2) мгновенную скорость и модуль мгновенной скорости в
указанные моменты времени
3) среднее ускорение за указанный промежуток времени
4) мгновенное ускорение и модуль мгновенного ускорения в
указанные моменты времени
s x2 x1
Решение: Средняя путевая скорость ср
t
t 2 t1
2
3
x1 2 4 4 4 0,2 4 59,2 м
112,8 59,2
26,8 м с
ср
2
3
6 4
x2 2 6 4 6 0,2 6 112,8 м
При прямолинейном движении мгновенная скорость в любой
момент времени
dx
t 2 8t 0,6t 2 м с
dt
Модуль мгновенной скорости в указанные моменты времени:
1 2 8 4 0,6 16 24,4 м / c
2 2 8 6 0,6 36 28,4 м / c

37.

Пример 19.
Уравнение движения точки по прямой имеет
вид x t 2t 4t 2 0,2t 3 м . Найти:
1)среднюю скорость за промежуток времени от t1=4c до t2=6c
2)мгновенную скорость и модуль мгновенной скорости в
указанные моменты времени
3)среднее ускорение за указанный промежуток времени
4)мгновенное ускорение и модуль мгновенного ускорения в
указанные моменты времени
Решение: Модуль среднего ускорения
а
2 1 28,4 24,4
2 м / c2
t
t2 t1
6 4
Мгновенное ускорение в любой момент времени
d
а t
8 1,2t м с 2
dt
Модуль мгновенного ускорения в указанные моменты времени:
a1 8 1,2 4 3,2 м / c
2
a2 8 1,2 6 0,8 м / c 2

38.

Пример 20. Машина идет по закругленному шоссе. Зависи-
мость радиуса-вектора
от времени задана уравнением:
r t 6i 8tj t 2 k м . Найти: 1)мгновенную скорость машины
и значение скорости в момент времени 3 с; 2) тангенциальное
и нормальное ускорение в указанный момент времени;
3) радиус кривизны шоссе.
Решение:
dr
Мгновенная скорость
t
Учитывая, что r xi yj zk
dt
8 j 2tk м с
2
dx
dy
dz
2
2
2
2
м
8
2
t
0 y
8 м
2
t
x
y
z
z
с
с
dt
dt
dt
2
Подставив t=3 c, получаем 64 2 3 10 м с
2
Полное ускорение a d dt 2 м с знак «–» указывает, что движение
машины замедленное (модуль скорости уменьшается)
2
d d 82 2t
4 2t
4t
Тангенциальное ускорение а
2
2
2
2
dt
dt
2
8
2
t
8
2
t
Подставив t=3 c а 1,2 м с 2
x
an a 2 a 2
an 1,6 м с 2
Радиус кривизны окружности R
2
an
100
62,5 м
1,6

39.

Пример 21. Автомобиль движется по выпуклому мосту.
Траектория движения автомобиля изменяется по закону
S (t ) 3t 3 36t 2 159t 7 м ; время t - в секундах. Определить
скорость и ускорение центра масс автомобиля в тот момент
времени, когда он находится на вершине моста, а радиус
кривизны траектории 80 м.
Решение:
Мгновенная скорость dS
9t 2 72t 159, м
dt
с
d
18t 72, м 2
По определению ускорения а
с
dt
где R - радиус кривизны траектории в данный момент времени.
Определим момент времени t0, когда автомобиль находится на вершине
моста, т.к. в этот момент времени скорость автомобиля достигает минимума и а d 0, м 2
18t 72 0, t0 4 c
dt
с
2
Т.о. скорость на вершине моста 0 9t0 72t0 159 15 м с
2
2
м 2
2 225
a
a
a
3
Полное
ускорение
м
0
n
an
2,8125
с
с2
R
80
Направление полного ускорения совпадает с направлением нормального
ускорения, т.е. вектор
a0 направлен вертикально вниз.

40.

Пример 22. Даны уравнения движения точки (время t - в
секундах). x(t ) t 3 5, м; y(t ) 3t 2 , м; z (t ) 6t 7, м
Найти радиус кривизны траектории в точке, где скорость
движения точки 33 м/с.
Решение: Найдем проекции скорости движения точки на оси координат
dy
м
dx
dz
м
2 м
6
t
,
y
x
3t ,
z 6
dt
с
dt
с
dt
с
2
2
2
4
2
Модуль вектора скорости x y z 9t 36t 36
33 9t 4 36t 2 36
Возведем в квадрат правую и левую части уравнения и получим
9t 4 36t 2 1053 0
2
корни уравнения: t1 13 (не имеет смысла)
t 3 c
t22 9
Найдем проекции ускорения на оси координат
d z
м
d y
d x
м
м
a
0
2
z
ax
6t 2
ay
6 2
dt
с
dt
dt
с
с 2 2 2
м
2
Модуль вектора полного ускорения:a a x a y a z 36t 36 0 6 10 2
с
d
36t 3 72t
м
a
18 2 Нормальное ускорение
dt 2 9t 4 36t 2 36
с
2 332
R
181,5 м
an a 2 a 2 360 324 6 м с
an
6

41.

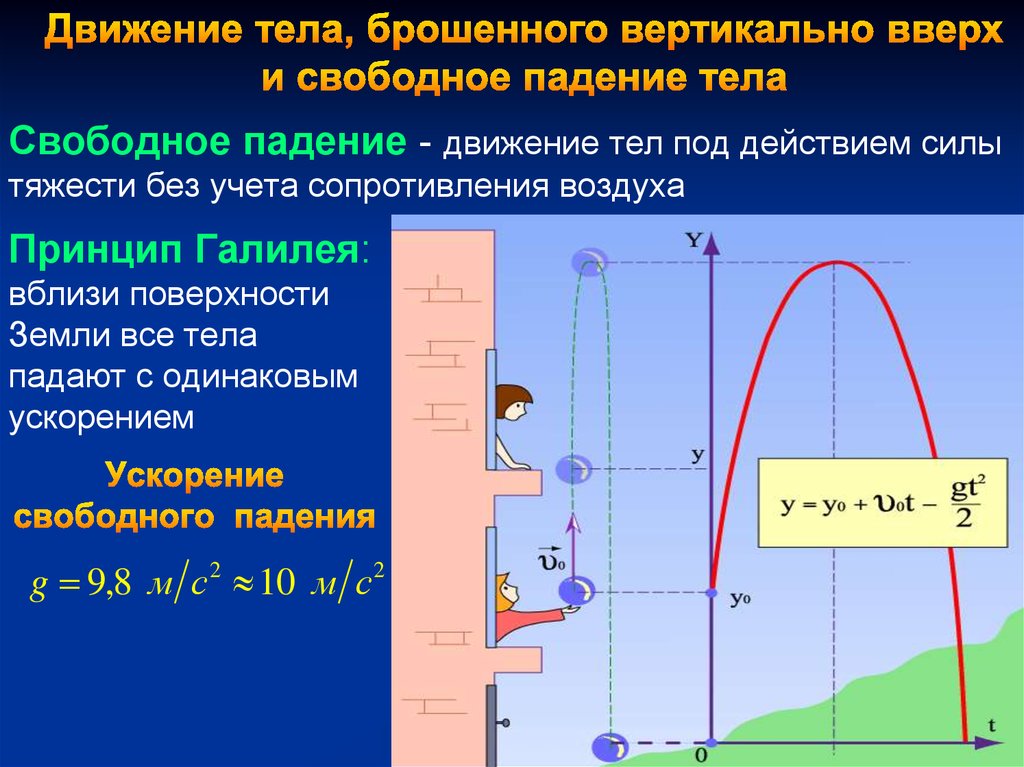
Свободное падение - движение тел под действием силы
тяжести без учета сопротивления воздуха
Принцип Галилея:
вблизи поверхности
Земли все тела
падают с одинаковым
ускорением
g 9,8 м с 2 10 м с 2

42.

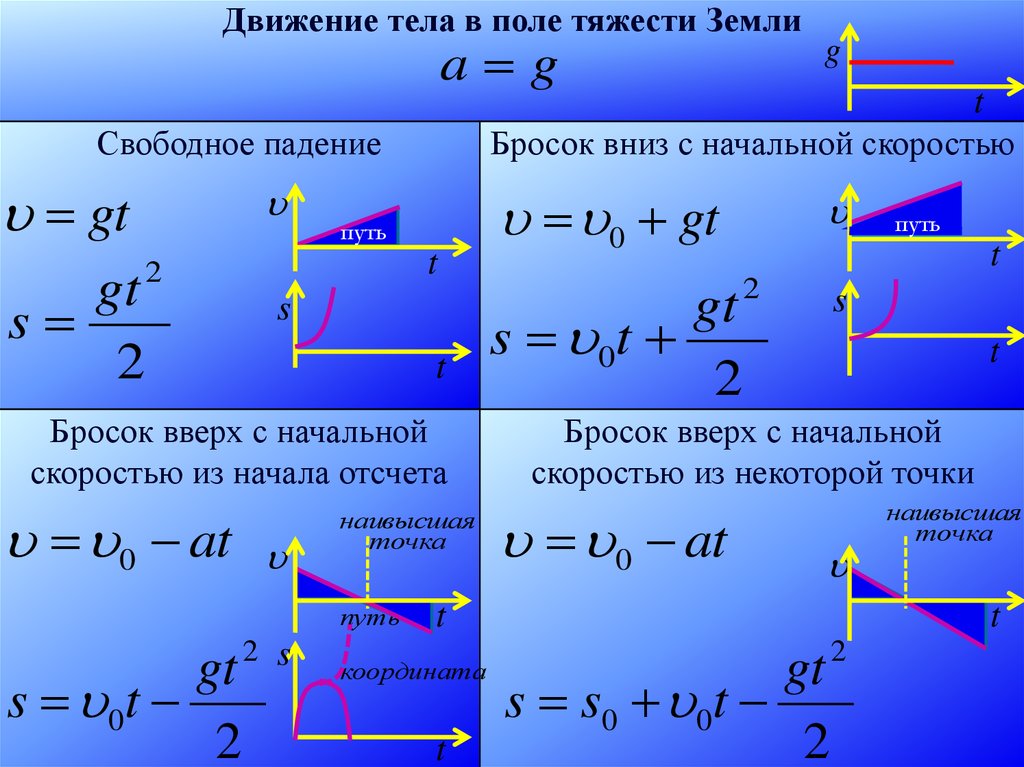
Движение тела в поле тяжести Земли
a g
t
Бросок вниз с начальной скоростью
Свободное падение
gt
gt
s
2
путь
t
2
s
t
Бросок вверх с начальной
скоростью из начала отсчета
0 at
наивысшая
точка
путь
gt
s 0t
2
2 s
g
0 gt
gt
s 0t
2
t
2
s
t
Бросок вверх с начальной
скоростью из некоторой точки
0 at
t
координата
t
путь
наивысшая
точка
t
gt
s s0 0t
2
2

43.

Пример 24. Тело брошено вертикально вверх с
начальной скоростью 20 м/с. Каков модуль скорости тела
через 0,5 с после начала движения? Сопротивлением
воздуха пренебречь.
Решение: При равнозамедленном движении в поле
тяжести земли 0 gt
В наивысшей точке подъема ʋ=0 и скорость поменяет знак.
Тогда 20 10 0,5 15 м с
Ответ: 15 м/с

44.

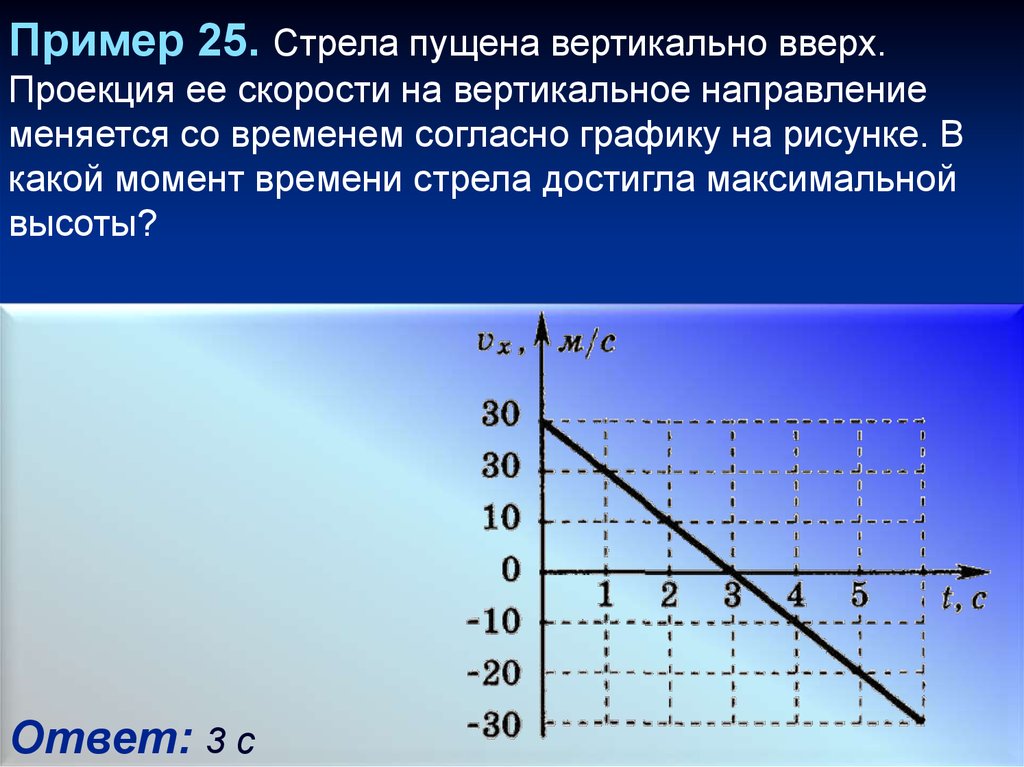
Пример 25. Стрела пущена вертикально вверх.
Проекция ее скорости на вертикальное направление
меняется со временем согласно графику на рисунке. В
какой момент времени стрела достигла максимальной
высоты?
Ответ: 3 с

45.

Пример 26. Стрела выпущена из лука вертикально вверх с
башни высотой 30 м со скоростью 30 м/с. У основания башни находится ров глубиной 5 м. Пренебрегая сопротивлением воздуха,
определить: 1) время подъема на максимальную высоту и максимальную высоту подъема 2) время полета стрелы до падения на
дно рва, скорость стрелы в момент падения и путь, который
пролетела стрела за это время
Решение: Направим координатную ось вертикально вверх
Совместим начало отсчета с точкой выстрела
Вначале движение стрелы - равнозамедленное hmax
0
из начала отсчета
gt 2
h 0t
y 0 gt
g
2
h1
В наивысшей точке подъема время t t1
скорость y 0 Тогда 0 0 gt1 , 0 gt1
Время подъема на максимальную высоту
h2
0 30
t1
3 с Максимальная высота подъема
g
hmax
10
2
0 g 0 2 0 2
gt1
30 2
0
0t1
45 м
2
g
2g
2g
20
2

46.

Пример 26. Стрела выпущена из лука вертикально вверх с
башни высотой 30 м со скоростью 30 м/с. У основания башни находится ров глубиной 5 м. Пренебрегая сопротивлением воздуха,
определить: 1) время подъема на максимальную высоту и максимальную высоту подъема 2) время полета стрелы до падения на
дно рва, скорость стрелы в момент падения и путь, который
пролетела стрела за это время
Решение: Рассмотрим движение стрелы из
верхней точки. Т.к. в наивысшей 2точке скорость
равна нулю ( y 0 ), то h gt 2 ,
2
где h hmax h1 h2 , а t2 время падения
2 hmax h1 h2
2h
2 45 30 5
t2
4 c
g
g
10
Общее время полета стрелы t t1 t2 3 4 7 c
Полный путь стрелы
hпол 2hmax h1 h2 90 30 5 125 м
Скорость стрелы в момент падения
hmax
0
g
h1
h2
y gt 2 10 4 40 м / с

47.

Пример 27. Тело падает с высоты 0,5 км с нулевой
начальной скоростью. Пренебрегая сопротивлением
воздуха, определите, какое время понадобится телу для
прохождения
последних 100 м пути.
500 м
Решение: Чтобы найти время t1, затраченное на
h2
h
h1
прохождение последних 100 м, удобно от времени
t всего пути (500 м) отнять время t2, затраченное на
прохождение первых 400 м:
t1 t t2
Уравнение движения при падении тела с
высоты без начальной скорости
gt 2
2h
2h2
h
t
t2
100 м
g
2
g
t1
2h 2h2
2 500 2 400
100 80 10 8,94 1,06 c
g
g
10
10
Высота телебашни в Москве 536 м

48.

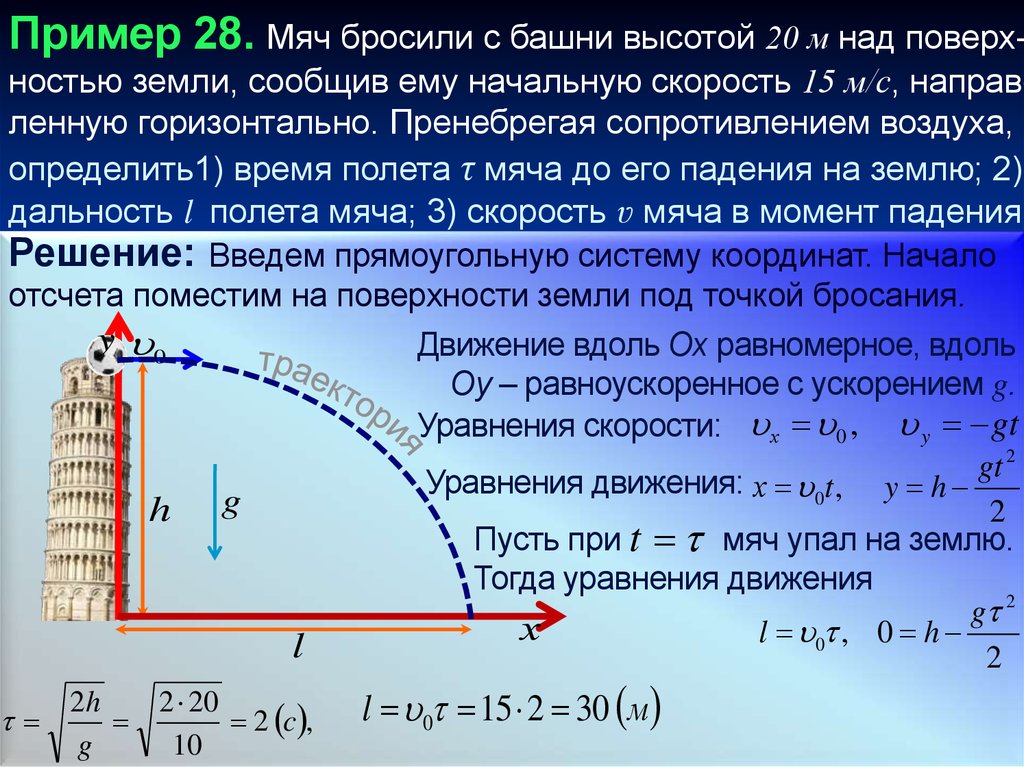
Пример 28. Мяч бросили с башни высотой 20 м над поверх-
ностью земли, сообщив ему начальную скорость 15 м/с, направленную горизонтально. Пренебрегая сопротивлением воздуха,
определить1) время полета τ мяча до его падения на землю; 2)
дальность l полета мяча; 3) скорость ʋ мяча в момент падения
Решение: Введем прямоугольную систему координат. Начало
отсчета поместим на поверхности земли под точкой бросания.
y 0
Движение вдоль Ох равномерное, вдоль
Оy – равноускоренное с ускорением g.
Уравнения скорости: х 0 , y gt
h
g
l
2h
2 20
2 c ,
g
10
gt 2
Уравнения движения: х 0t , y h
2
Пусть при t мяч упал на землю.
Тогда уравнения движения
g 2
х
l 0 , 0 h
2
l 0 15 2 30 м

49.

Пример 28. Мяч бросили с башни высотой 20 м над поверхностью земли, сообщив ему начальную скорость 15 м/с,
направленную горизонтально. Пренебрегая сопротивлением
воздуха, определить 1) время полета τ мяча до его падения
на землю; 2) дальность l полета мяча; 3) скорость ʋ мяча в
момент падения.
Решение: Уравнения скорости в момент падения
y 0
2h
х 0 , y g g
2 gh
g
Отметим эти направления на рисунке
Скорость в момент падения находим
по правилу параллелограмма
h
х
l
y
х
х2 y2 02 2 gh
152 2 10 20 25 м / с

50.

Пример 29. По лежащей на столе монете щелкнули так, что
она, приобретя скорость ʋ, слетела со стола. Через время t
модуль скорости монеты будет равен
1) gt
2)
3) gt
4) g t
2
2 2
Решение: При броске горизонтально происходит
сложение скоростей
х2 y2 02 gt 2
х
у 0
0
у
1
х
у
х
2
у
Ответ: 4
х

51.

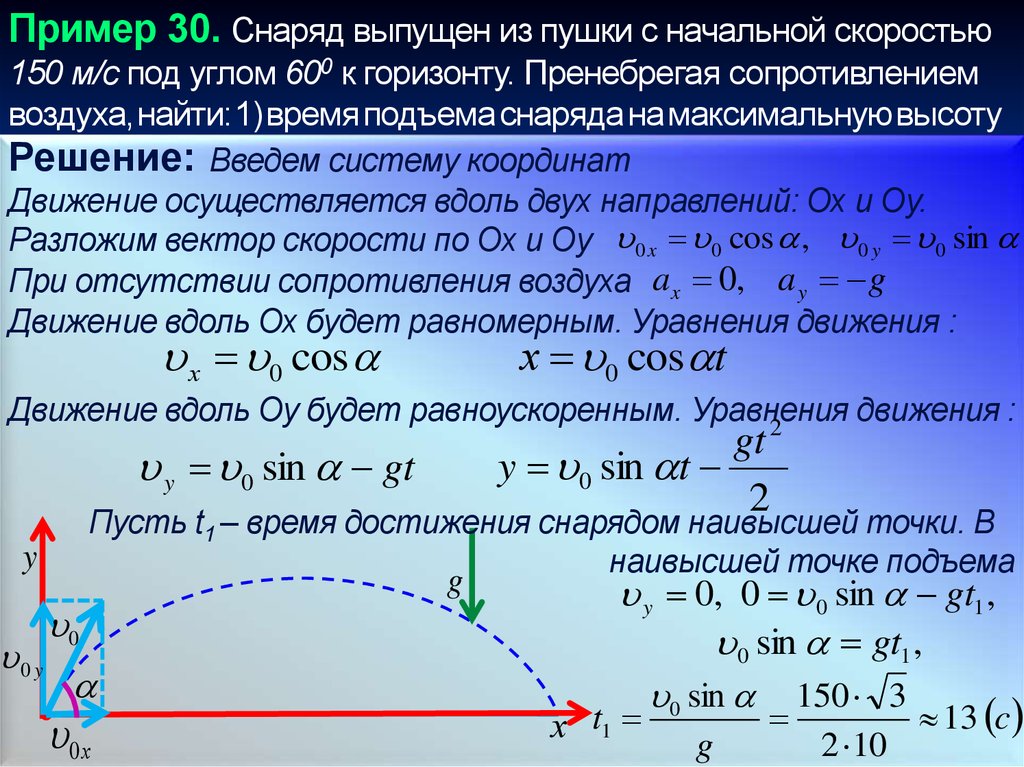
Пример 30. Снаряд выпущен из пушки с начальной
скоростью 150 м/с под углом 600 к горизонту. Пренебрегая
сопротивлением воздуха, определить: 1) время подъема
снаряда на максимальную высоту; 2) наибольшую высоту
подъема снаряда; 3) дальность полета снаряда; 4) время
полета до момента падения снаряда на землю; 5) скорость в
момент его падения на землю; 6) радиус кривизны
траектории снаряда в ее наивысшей точке; 7) уравнение
траектории снаряда

52.

Пример 30. Снаряд выпущен из пушки с начальной скоростью
150 м/с под углом 600 к горизонту. Пренебрегая сопротивлением
воздуха,найти:1)времяподъемаснаряданамаксимальнуювысоту
Решение: Введем систему координат
Движение осуществляется вдоль двух направлений: Ох и Оy.
Разложим вектор скорости по Ох и Оy 0 x 0 cos , 0 y 0 sin
При отсутствии сопротивления воздуха a x 0, a y g
Движение вдоль Ох будет равномерным. Уравнения движения :
х 0 cos t
х 0 cos
Движение вдоль Оy будет равноускоренным. Уравнения
движения :
2
gt
y 0 sin t
2
y 0 sin gt
Пусть t1 – время достижения снарядом наивысшей точки. В
наивысшей точке подъема
y
0 y
0
0 х
g
y 0, 0 0 sin gt1 ,
0 sin gt1 ,
х t1
0 sin
g
150 3
13 c
2 10

53.

Пример 30. Снаряд выпущен из пушки с начальной
скоростью 150 м/с под углом 600 к горизонту. Пренебрегая
сопротивлением воздуха, определить: 2) наибольшую высоту
подъема снаряда; 3) дальность полета снаряда;
Решение:
Зная время подъема на максимальную высоту
И уравнение движения вдоль Оy, получим
t1
2
0 sin
g
13 c
0 sin g 0 sin 0 2 sin 2
gt
y 0 sin t
0 sin
2
g2
2 g
2g
150 0,75
0 2 sin 2
hmax
843,75 м
hmax
20
2g
2 sin
Зная время полета снаряда t 2t1 0
26 c
g
y
и уравнение движения вдоль Ох, получим
2
2 0 sin 0 sin 2
х 0 cos
g2
g
hmax
2
0 sin 2 150 3
1948,6 м
х S
g
2 10
2

54.

Пример 30. Снаряд выпущен из пушки с начальной
скоростью 150 м/с под углом 600 к горизонту. Пренебрегая
сопротивлением воздуха, определить: 5) скорость в момент
его падения на землю;
Решение: Скорость снаряда в любой момент времени
x2 y2
y 0 sin g
х 0 cos
0 sin
Где время движения уже найдено 2
26 c
В момент падения на землю
2 0 sin
g
y 0 sin g
0 sin
y
g
2
2
0 cos 0 sin 0 150 м / c
0
х
0 х
y
х

55.

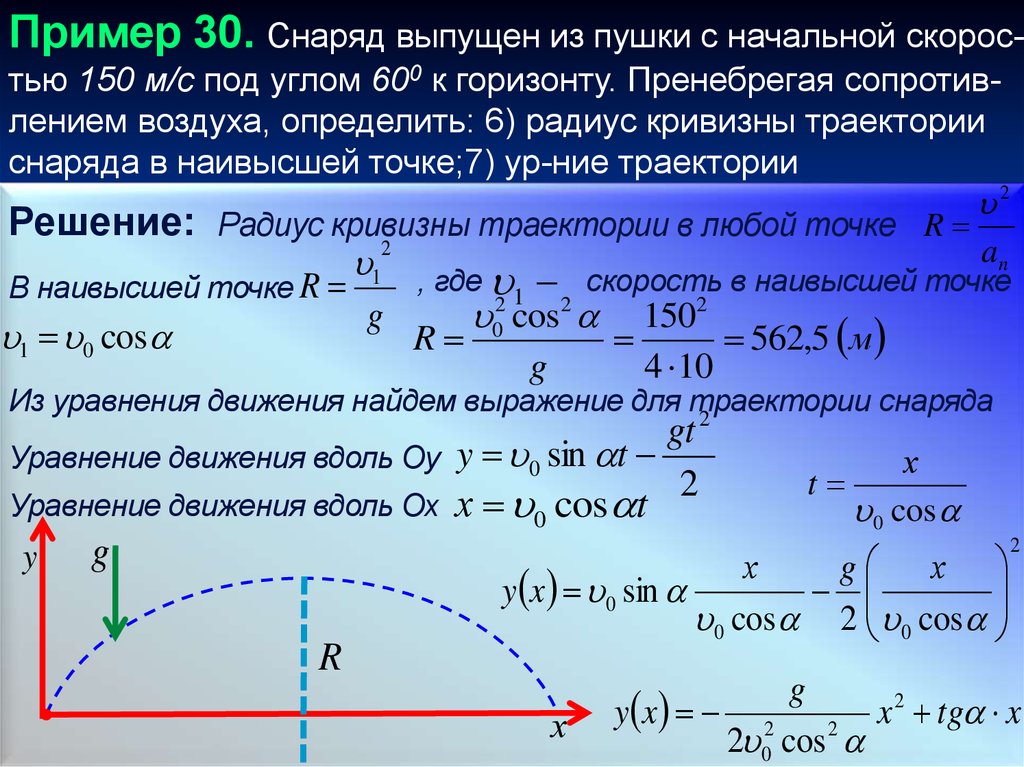
Пример 30. Снаряд выпущен из пушки с начальной скоростью 150 м/с под углом 600 к горизонту. Пренебрегая сопротивлением воздуха, определить: 6) радиус кривизны траектории
снаряда в наивысшей точке;7) ур-ние траектории
2
Решение: Радиус кривизны
траектории в любой точке R
2
an
1 , где
1 скорость в наивысшей точке
В наивысшей точке R
g
1 0 cos
R
02 cos2
g
1502
562,5 м
4 10
Из уравнения движения найдем выражение для траектории
снаряда
2
gt
Уравнение движения вдоль Оy y 0 sin t
2
Уравнение движения вдоль Ох
y
g
R
х 0 cos t
t
х
0 cos
х
g х
y x 0 sin
0 cos 2 0 cos
х
y x
2
g
2
x
tg x
2
2
2 0 cos

56.

Пример 31. Небольшой камень бросили с ровной
горизонтальной поверхности земли под углом к
горизонту. На какую максимальную высоту поднялся
камень, если ровно через 1 с после броска его скорость
была направлена горизонтально?
Решение: Скорость будет направлена горизонтально в
максимальной точке подъема → время достижения максимальной
высоты t=1 c
Вдоль оси у движение равнопеременное. В проекции на ось у
скорость у 0 sin gt ,
Так как в наивысшей точке у 0, то
0 sin gt ,
Подставим это значение в уравнение движения
2
2
2
gt 2
gt
gt
10
1
y 0 sin t
gt 2
5 м
2
2
2
2
Ответ: 5 м

57.

Пример 32. Тело брошено под углом к горизонту.
Оказалось, что максимальная высота подъема в 2 раза
меньше дальности полета. Пренебрегая сопротивлением
воздуха, определите угол броска к горизонту.
Решение: Максимальная высота подъема
0 sin 2
2g
2
hmax
дальность полета
По условию
2hmax S
0 sin 2
02 sin 2
2
2
2g
Ответ:
g
02 sin 2
S
g
, sin 2 cos , tg 2, arctg 2

58.

заключается в том, что по известному значению
ускорения a(t) найти скорость точки и восстановить
уравнение движения r(t).
По определению
отсюда
или, так как
Следовательно
12.09.2017 17:58:43
d (t )
a(t )
,
dt
(t ) a(t )dt
dr t
(t )
,
dt
r (t ) (t )dt

59.

Пример 33. Ракета начала движение со скоростью,
определяемой выражением (t ) 6t 2t , м c .
Какой путь пройдет ракета за 2 мин?
Решение: Путь найдем как s(t ) (t )dt
2
s(t ) (6t 2 2t )dt 2t 3 t 2 С, м
По условию С s(t0 ) путь в момент времени
t t0 0 c
В начальный момент скорость ракеты (t0 ) 0
Если за начало координат взять точку начала
движения, то С s(t0 ) 0
s(t ) 2t 3 t 2 , м
за 2 минуты
s(t )t 120 2 1203 120 2 3441600 м
Отметим, что скорость ракеты при взлете
12.09.201728
17:58:43
порядка
км/с

60.

Пример 34. Автомобиль начал движение со скоростью,
определяемой выражением (t ) 3t 2 8t , м c . Найти среднюю скорость автомобиля в интервале времени от 2с до 5с
Решение: Путь найдем как s(t ) (t )dt
s (t ) (3t 2 8t )dt t 3 4t 2 С, м
По условию С s(t0 ) путь в момент времени t t0 0 c
Если за начало координат взять точку начала движения, то
С s(t0 ) 0
t1 2 c t2 5 c
s s t1 s t2 53 4 52 23 4 22 33 м
S 33
Средняя скорость
11 м с
t 3

61.

Пример 35. Автомобиль начал движение с ускорением,
определяемым выражением a(t ) 3t 2 8t 1, м c 2 . Найти
скорость автомобиля в момент времени t=2с.
(t ) a(t )dt
Решение: Скорость найдем как
(t ) (3t 2 8t 1)dt t 3 4t 2 t C
По условию С (t0 ) скорость в момент времени t t0 0 c
Так как автомобиль начинал движение, то его начальная
скорость
С 0
(t0 ) 0
(t ) t 3 4t 2 t
В момент времени t=2 с: 23 4 22 2 10 м с
Т.е. автомобиль движется в направлении, противоположном
положительному направлению оси Ох
0
, м с

62.

Пример 36. Луноход начал движение с ускорением
a(t ) 6 2t , м мин 2 . Найти через 6 минут среднюю и
максимальную скорости движения лунохода.
t2
Решение: Скорость лунохода (t ) a(t )dt
6
t
2
(t ) a(t )dt 6t t С м мин
1
0
По условию
С (t0 ) скорость в момент времениt t0
Так как он начинал движение, то его начальная скорость (t0 ) 0
(t ) 6t t 2 , м мин
При t 6 c 0 м мин луноход остановился
s
По определению, средняя путевая скорость
6
1 3
t
2
3
t
t
C
,
м
Путь s(t ) (t )dt
3
0
Если за начало координат взять точку начала движения, то
С s(t0 ) 0
1 3
Путь за 6 минут s s 6 s 0 3 6 6 0 36 м
3
36
6 м мин
Средняя скорость
2
6

63.

Пример 37. Луноход начал движение с ускорением
a(t ) 6 2t , м мин 2 . Найти через 6 минут среднюю и
максимальную скорости движения лунохода.
Решение: Максимальное значение скорости можно найти с
помощью производной. Но в данной задаче производная от
скорости (ускорение) – дана.
a(t ) 6 2t , м мин 2
a(t ) 0 при t 3 c
Максимальной скорости луноход достигает через 3с после
начала движения
(t ) 6t t 2 , м мин
(3) 18 9 9 м мин
(t), м мин
9
0 3
6
t, c

64. Кинематика твердого тела

Различают пять видов движения твердого тела:
- поступательное;
- вращательное вокруг неподвижной оси;
- плоское;
- вокруг неподвижной точки;
- свободное.
Поступательное движение и вращательное
движение вокруг оси – основные виды движения
твердого тела.
Остальные виды движения твердого тела можно свести к
одному их этих основных видов или к их совокупности

65. Поступательное движение твердого тела

Поступательное движение – такое движение
твердого тела, при котором любая прямая, связанная с телом,
остается параллельной своему начальному положению и все
точки твердого тела совершают равные перемещения
Скорости и ускорения всех точек
твердого тела в данный момент
времени t одинаковы
Это позволяет свести изучение
поступательного движения твердого
тела к изучению движения
отдельной точки, т.е. к задаче
кинематики материальной точки

66.

При вращательном
движении все точки тела
движутся по окружностям,
центры которых лежат на
одной и той же прямой OO,'
называемой осью
вращения
Понятие вращательного
движения для
материальной точки
неприемлемо
О
О

67.

Пусть абсолютно твердое тело вращается вокруг
неподвижной оси ОО'
Рассмотрим движение некоторой точки М

68.

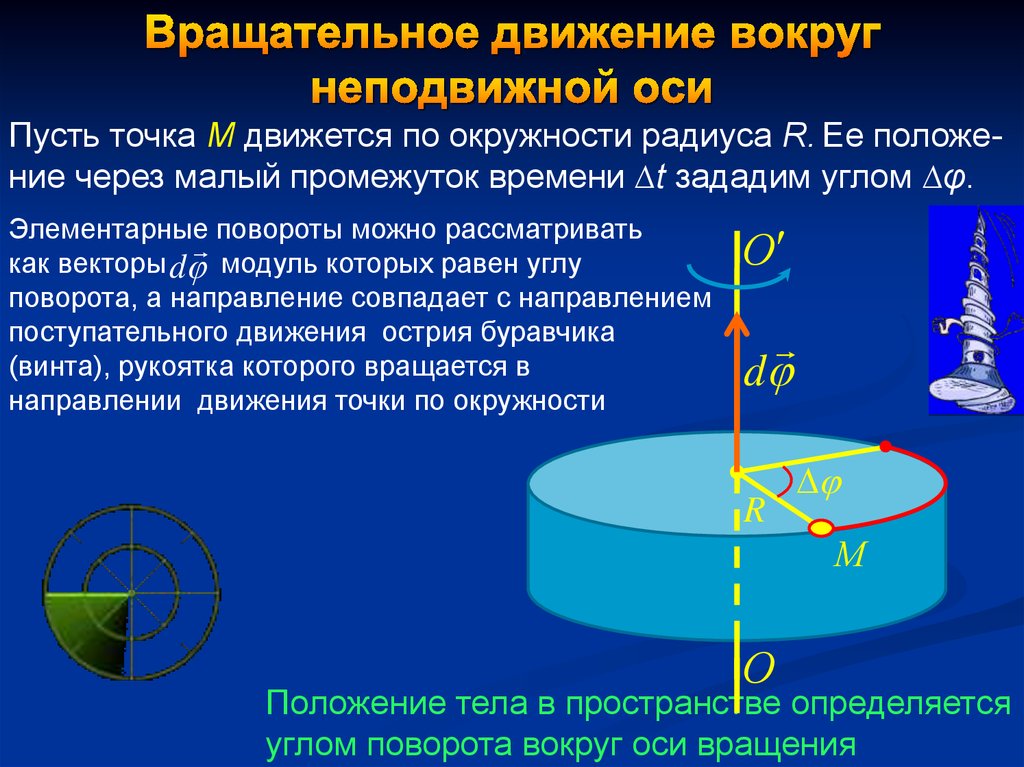
Пусть точка М движется по окружности радиуса R. Ее положение через малый промежуток времени ∆t зададим углом ∆φ.
Элементарные повороты можно рассматривать
как векторы d модуль которых равен углу
поворота, а направление совпадает с направлением
поступательного движения острия буравчика
(винта), рукоятка которого вращается в
направлении движения точки по окружности
О
d
R
М
О
Положение тела в пространстве определяется
углом поворота вокруг оси вращения

69.

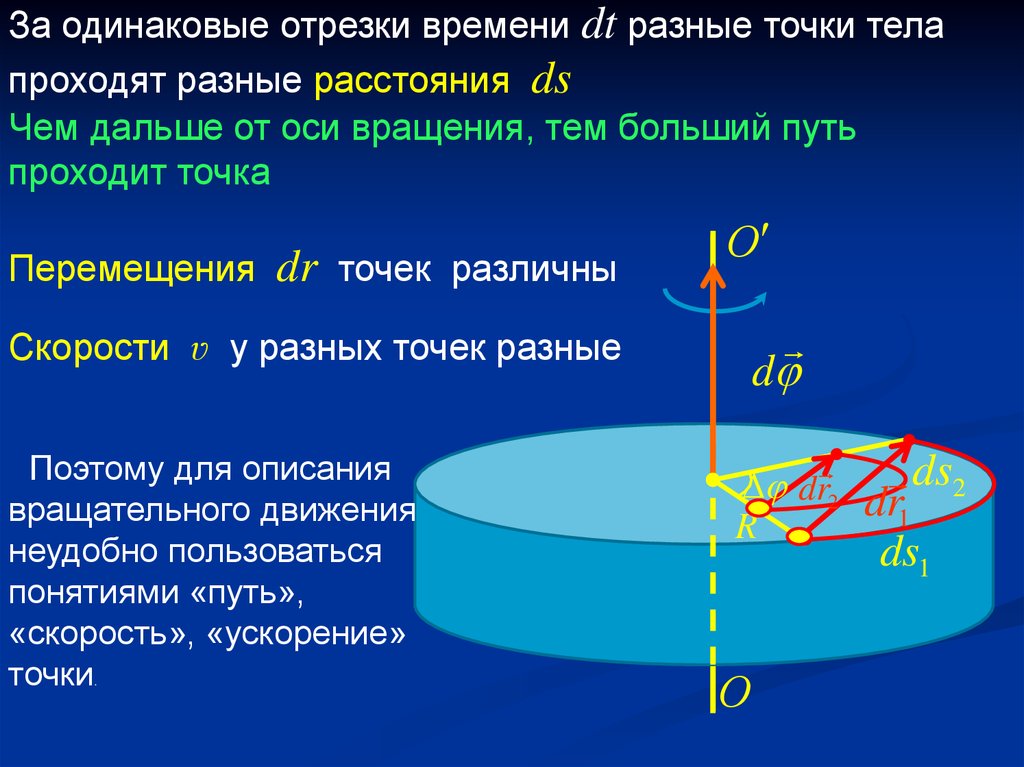
За одинаковые отрезки времени dt разные точки тела
проходят разные расстояния ds
Чем дальше от оси вращения, тем больший путь
проходит точка
Перемещения
dr точек различны
О
Скорости ʋ у разных точек разные
Поэтому для описания
вращательного движения
неудобно пользоваться
понятиями «путь»,
«скорость», «ускорение»
точки
.
d
dr2
R
О
ds2
dr1
ds1

70.

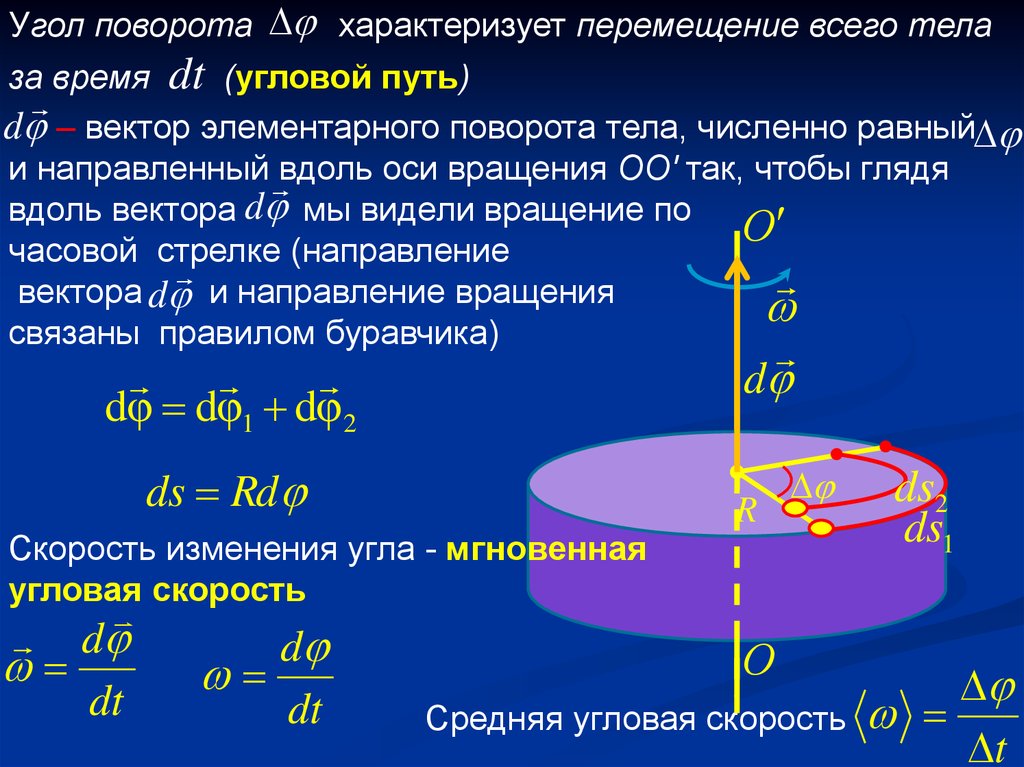
Угол поворота характеризует перемещение всего тела
за время dt (угловой путь)
d – вектор элементарного поворота тела, численно равный
и направленный вдоль оси вращения ОО' так, чтобы глядя
вдоль вектора d мы видели вращение по
О
часовой стрелке (направление
вектора d и направление вращения
связаны правилом буравчика)
d
dφ dφ1 dφ2
ds Rd
Скорость изменения угла - мгновенная
угловая скорость
d
dt
d
dt
R
О
Средняя угловая скорость
ds2
ds1
t

71.

СЛЕДСТВИЕ 1
Поскольку
ds Rd
Интегрируя правую и левую части равенства, получим:
s R C
где в начальный момент времени t 0
постоянная интегрирования C s0
но при движении по окружности обычно полагают s0 0
и получаем формулу, связывающую путь и угол поворота:
s R

72.

СЛЕДСТВИЕ 2
Поскольку
Элементарный поворот
d
dt
d dt
Элементарное перемещение
постоянная интегрирования
ds Rd R dt
ds
R
dt
получаем формулу, связывающую линейную скорость и
угловую:
R

73.

Пример 68. Диск радиусом 20 см равномерно вращается
вокруг своей оси. Скорость точки, находящейся на расстоянии
15 см от центра диска, равна 1,5 м/с. Скорость крайней точки
диска равна
Решение: R
1 2 const
1 R1
2 R2
1 R2 1,5 0,2
2
2 м с
R1
0,15
R2
R1

74.

При движении с ускорением введем вектор углового
ускорения для характеристики неравномерного вращения
тела:
d
d
dt
dt
Вектор углового ускорения совпадает по направлению с
вектором угловой скорости в случае ускоренного вращения
0
и противоположен ему по направлению
в случае замедленного вращения
0
Среднее угловое ускорение
определяется как
t

75.

Все кинематические параметры,
характеризующие вращательное движение
(угловое ускорение, угловая скорость и угол
поворота)
направлены вдоль оси вращения

76.

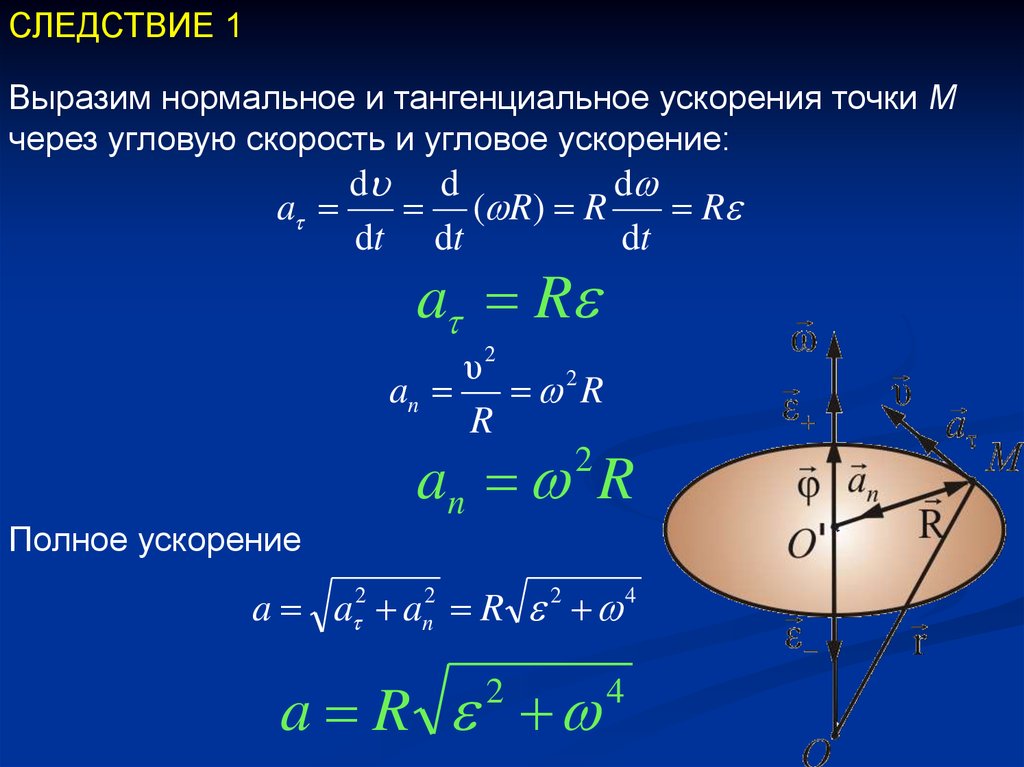
СЛЕДСТВИЕ 1
Выразим нормальное и тангенциальное ускорения точки М
через угловую скорость и угловое ускорение:
d d
d
a
( R) R
R
dt dt
dt
a R
υ2
an
2R
R
an R
2
Полное ускорение
a a 2 an2 R 2 4
a R
2
4

77.

Вели
чины
Поступательное движение
Длина пути
Кинетические характеристики
Связь между
величинами
Модуль скорости
Модуль
ускорения
d
a
dt
2
d s
dt 2
s R , где R
s f (t )
ds
dt
Полное ускорение
a a a
2
2
n
Тангенциальная
составляющая
ускорения
d
a
dt
Нормальная
составляющая
ускорения
an
2
R
Вращательное
движение вокруг
неподвижной оси
радиус вращения точки
Угол поворота
R
Модуль угловой
скорости
f (t )
d
dt
а R 2 4
a R
an 2 R
Модуль углового
ускорения
d d 2
2
dt
dt

78.

Сопоставляем
ые величины
Поступательное
движение
Кинематические уравнения
Равномерное движение
a 0
const
s s0 t
Равнопеременное
движение
Вращательное
движение вокруг
неподвижной оси
Равномерное вращение
0
const
0 t
Равнопеременное
вращение
const
a const
0 t
0 at
2
2
t
at
0 0 t
s s0 0t
2
2

79.

Период Т – промежуток времени, в течение которого тело совершает полный оборот (т.е. поворот на
угол 2 )
Т
Частота
2
ν – число оборотов тела за 1 сек.
1
ν
Т
Угловая скорость
2π
ω
2 πν
Т

80.

Если известно значение вектора ускорения, то по
формуле
d
dt
получим:
dt
В общем случае ускорение является функцией времени и
полученную формулу следует записывать таким образом:
t dt

81.

Если известно значение вектора скорости, то по формуле
d
dt
найдем элементарный угол поворота
d dt
Интегрируя правую и левую части равенства, получим:
dt
В общем случае скорость является функцией времени и
полученную формулу следует записывать таким образом:
t dt

82.

Простейшие случаи вращения тела вокруг
неподвижной оси:
- равномерное вращение
0 const
dt t C
в момент времени t t0 постоянная интегрирования C 0
0 t
-равнопеременное вращение const const
dt t C
в момент времени t t0 постоянная интегрирования C 0
0 t
t dt 0 t dt 0t
t
2
2
C
в момент времени t t0 постоянная интегрирования C 0
0 0 t
t 2
2

83.

Пример 38. Маховик вращался с постоянной частотой
8 об/c, потом начал вращаться равноускоренно. Через 8 с
вращение маховика опять сделалось равномерным, но уже
с частотой 16 об/c. Определить угловое ускорение
маховика и количество оборотов, сделанных маховиком за
время равноускоренного движения.
2
t
Решение: Уравнение движения 0 0t
2
уравнение скорости t
0
Пусть начальный угол поворота 0 0 . Т.к. 0 2 0
2 N
t 2
2
и 2 N 2 0t 2
рад
2 2 0 2 0 6,28 16 8
6
,
28
2
Из 1-го уравнения
8
с
t
t
2
Получаем 2 2 0 t
2 0 t
Из второго уравнения 2 N 2 0t
t
2
0 t 16 8 8
0 t
N
96 об
N 0t
2
2
2

84.

Пример 39. Маховик вращался с ускорением 2t 1 рад
.
2
Определить среднюю скорость вращения и количество с
оборотов, сделанных маховиком за 6 с от начала движения.
Решение: Средняя угловая скорость
Чтобы найти угол поворота за 6 с, найдем
t
2t 1 dt t 2 t C
Так как тело начало движение, то в момент времениt t0
C 0 0
1 3 1 2
2
Угол поворота t t dt t t C
3
2
Принимая начальный угол поворота C 0 0
При t 6 c
1 3 1 2
2 N 6 6 54
3
2
54
об
9
t
6
с
54
N
8,6
2