Похожие презентации:
Векторная алгебра
1. МАТЕМАТИКА 1 семестр бакалавры
Векторная алгебраI
Линейная алгебра
Аналитическая геометрия
Математический анализ:
II
Экзамен
Вычисление пределов и
производных, их применение.
Р.З.
К/Р №1
Р.З.
К/Р №2
2. Рекомендуемая литература
1. Бугров Я.С., Никольский С.М. Элементы линейнойалгебры и аналитической геометрии. М.: Наука,
1985.
2. Ильин В.А., Позняк Э.Г., Линейная алгебра. М.:
Наука, 1984.
3. Каган М.Л., Самохин М.В. Математика в
инженерном ВУЗе. Алгебра и геометрия. М.:
Стройиздат, 1984.
4. Каган М.Л., Кузина Т.С., Мацеевич Т.А. Векторная
алгебра – см. сайт МГСУ, каф. Высшей математики
5. Каган М.Л., Кузина Т.С., Мацеевич Т.А.
Аналитическая геометрия – см. сайт МГСУ, каф.
Высшей математики
3. Образец титульного листа расчетных заданий
Московский государственный строительный университетРасчетное задание № ___
по теме: «______________________
______________________________»
студента: ИСА I - ____
____ Фамилия Имя Отчество ____
Вариант № ____
2013г.
4. Лекция №1 Векторная алгебра
1. Векторные и скалярные величины. Понятия вектора, егомодуля, нулевого вектора.
2. Коллинеарные и компланарные векторы. Равенство
векторов.
3. Свободный вектор. Операции над векторами.
4. Понятие противоположного вектора и орта вектора.
5. Признак коллинеарности векторов.
6. Теорема о разложении вектора на плоскости и в
пространстве.
7. Прямоугольные координаты вектора и точки.
8. Операции над векторами в прямоугольной системе
координат.
5. Векторные и скалярные величины
Величиныскалярные
векторные
вполне определяются числом
определяются числом и
направлением
(на плоскости и в пространстве)
масса
время
скорость
сила
6.
Определение. Вектор AB направленный отрезок, началокоторого находится в точке A , а конец в точке B .
AB, AB, a …
Обозначение:
Определение. Длиной (модулем) вектора AB называется
расстояние между началом A и концом B этого вектора.
AB , AB , a …
Обозначение:
7.
Определение. Вектор, длина которого равна 0 (нулю) –называется нулевым вектором
Обозначение:
0
Направление нулевого вектора
8.
Определение. Ненулевые векторы называются коллинеарными,если они лежат либо на одной прямой, либо на параллельных
прямых.
a || b
Обозначение:
a b, a c, a d
9.
Определение. Векторы a и b называются равными (a b) ,если: 1) | a | | b |
2) a b
Равные векторы могут быть получены один из другого
параллельным переносом
a b
Будем рассматривать свободные векторы, т.е. для любого
вектора точка приложения может быть выбрана где угодно.
10.
Определение. Ненулевые векторы называются компланарными,если они лежат либо в одной плоскости, либо в параллельных
плоскостях.
Рассматриваем свободные векторы. Поэтому, если все
компланарные векторы привести к одному началу, то они будут
лежать в одной плоскости.
11. Линейные операции над векторами.
1. Сложение векторов.правило треугольника
правило параллелограмма
Свойства сложения
1. a b b a
2. a b c a b c
3. a 0 a
(переместительный закон)
(сочетательный закон)
12. Линейные операции над векторами.
2. Разность векторов.13. Линейные операции над векторами.
3. Умножение вектора на число.Определение. Произведением ненулевого вектора a на число
называется
вектор
такой,
что
c a
R, 0 ,
1) | c | | a | | | | a |
2) c | | a
3) c a , если 0
c a , если 0
a 0 a 0
0 a 0
14. Линейные операции над векторами.
Свойства умножения вектора на число.Пусть , R
1) a a
2) a a a
(распределительный закон)
3) a b a b
(распределительный закон)
4) 1 a a
Определение. Вектор
1 a
a
называется
противоположным вектору a .
a a 0
| a | | a |
вектором
15.
Определение. Единичным вектором (или ортом) вектора aназывается вектор который:
1) коллинеарен и сонаправлен вектору a
2) имеет длину равную 1
Обозначение:
0
a или e a
0
1) a a
2) a
0
1
16. Признак коллинеарности векторов в векторной форме
Теорема. Ненулевые векторы a и b коллинеарны тогда итолько тогда, когда один из них может быть получен из д ругого
умножением на некоторое число
a || b
a b, R .
Достаточность:
Доказательство:
Дано:
a b .
Доказать:
a || b
a b
b || b a || b .
17. Признак коллинеарности векторов в векторной форме
Необходимость:Дано:
a || b .
Доказать:
a b
Доказательство:
1) если a 0 , то 0 b 0 a
2) если a 0, b 0, a b
a
b
, 0
b
a
b
b
b
a
b
a
b
b
b a
b b, a b a b
Итак a b и a b a b .
18. Признак коллинеарности векторов в векторной форме
3) если a 0, b 0, a ba
b
, 0
b
a
b
b
b
a
a
b
b
b a
b
b b, a b a b
Итак a b и a b a b .
19.
Определение. Пусть даны векторы a1 , a2 ,..., an и действительныечисла 1 , 2 ,..., n . Вектор
a 1 a1 2 a2 ... n an
называется линейной комбинацией векторов
коэффициентами 1 , 2 ,..., n .
a1 , a2 ,..., an
с
Определение. Базис векторов это множество таких векторов в
векторном пространстве, что любой вектор этого пространства
может быть единственным образом представлен в виде
линейной комбинации векторов из этого множества.
20.
Теорема. (О разложении вектора на плоскости по базису двухнеколлинеарных векторов)
Если a || b , то любой ненулевой вектор c на плоскости может
быть представлен в виде линейной комбинации векторов a и b
c 1, 2 R, 21 22 0 : c 1 a 2 b
и такое представление единственное.
Дано:
a || b , 1 , 2 R , a, b, c компланарны.
Доказать:
c 1 a 2 b .
21.
Доказательство:Докажем возможность разложения:
ПКВ
OA || a
OA 1 a
ПКВ
OB || b OB 2 b
с OA OB 1 a 2 b
22.
Докажем единственность разложения:От противного:
Пусть с 1 a 2 b и с 3 a 4 b , 1 3 , 2 4 .
1 a 2 b 3 a 4 b
Тогда ( 1 3 ) a ( 4 2 ) b
4 2
a
b b, 0
1 3
a || b противоречит условию
разложение единственное.
23.
Теорема. (О разложении вектора в пространстве по базисутрёх некомпланарных векторов)
Если векторы a, b, c , некомпланарны, то любой ненулевой
вектор d , d 0 , в трехмерном пространстве может быть
представлен в виде линейной комбинации векторов a , b и c
d 1 , 2 , 3 R, 21 22 23 0 : d 1 a 2 b 3 c
и такое представление единственное.
24.
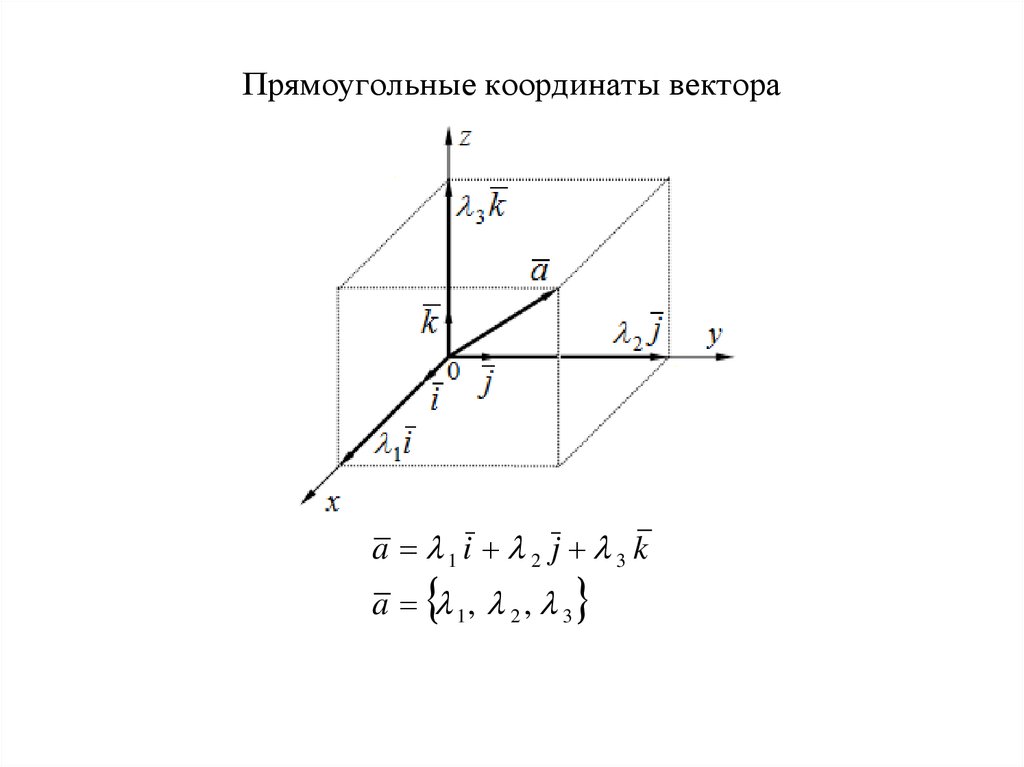
Прямоугольные координаты вектораa 1i 2 j 3 k
a 1 , 2 , 3
25.
Операции над векторами в прямоугольной системе координатa ax , a y , az , b bx , by , bz
1) a b ax bx , a y by , az bz
2) R, a a x , a y , a z
3) a b ax bx , a y by , az bz
26. Признак коллинеарности векторов в координатной форме
Теорема. Векторы a и b коллинеарны тогда и только тогда,когда их координаты пропорциональны.
ax a y az
a || b
bx by bz
























 Математика
Математика








