Похожие презентации:
Функции. Определение функции
1. ФУНКЦИИ
2. 1.Определение функции
• Пусть заданы множества Х и У. x X y YЕсли каждому элементу х по какому-то правилу f,
поставлен в соответствие один и только один
элемент у, то говорят, что на множестве Х задана
функция f со значением из множества У и пишут:
f: X→Y или y f ( x),
X
f
x
x X
Y
y
3.
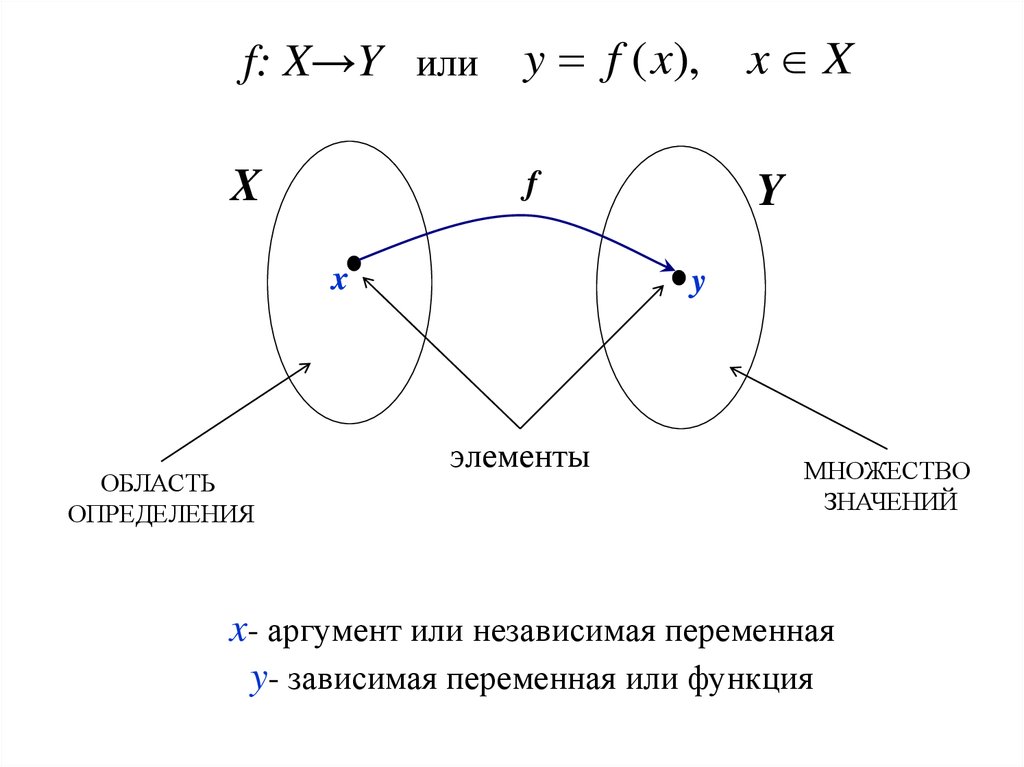
f: X→Y или y f ( x),x X
X
Y
f
x
ОБЛАСТЬ
ОПРЕДЕЛЕНИЯ
y
элементы
МНОЖЕСТВО
ЗНАЧЕНИЙ
x- аргумент или независимая переменная
y- зависимая переменная или функция
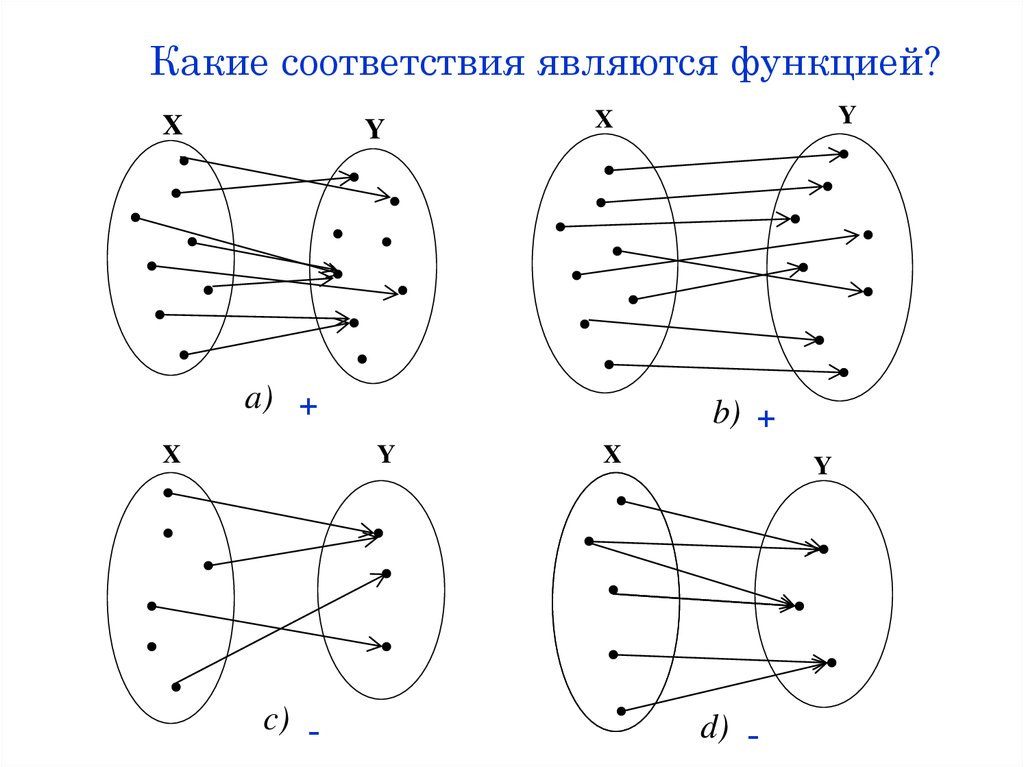
4. Какие соответствия являются функцией?
XY
a) +
X
b) +
Y
c) -
Y
X
X
Y
d) -
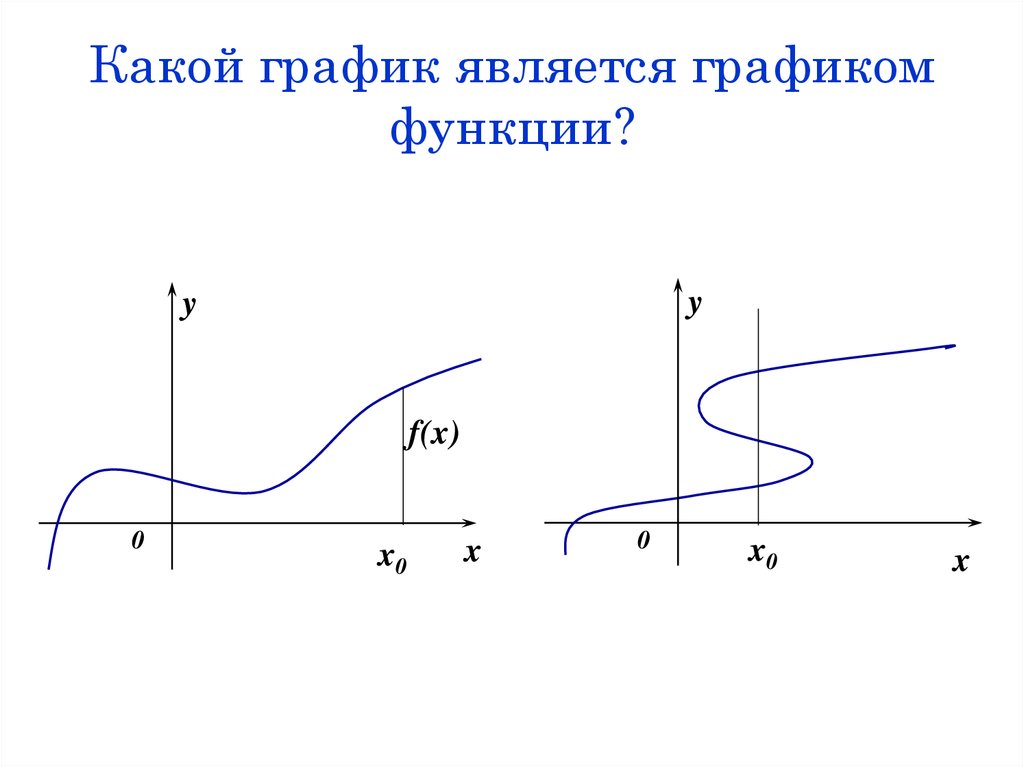
5. Какой график является графиком функции?
yy
f(x)
0
x0
x
0
x0
x
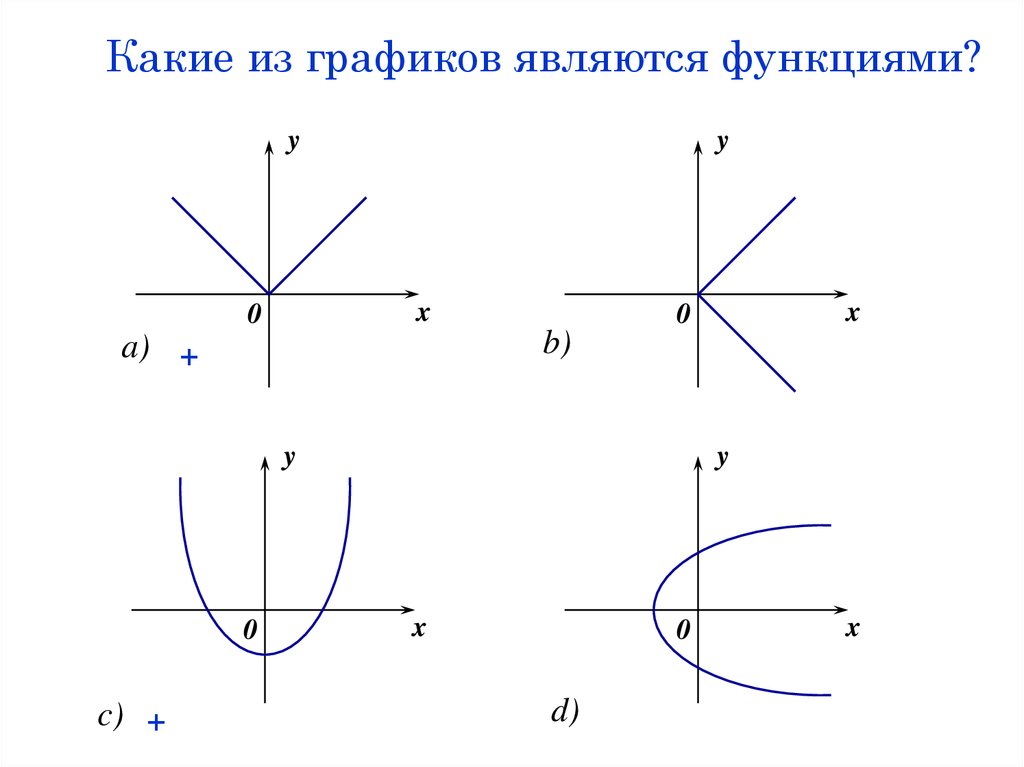
6. Какие из графиков являются функциями?
yy
x
0
b)
a) +
y
0
c) +
x
0
y
x
0
d)
x
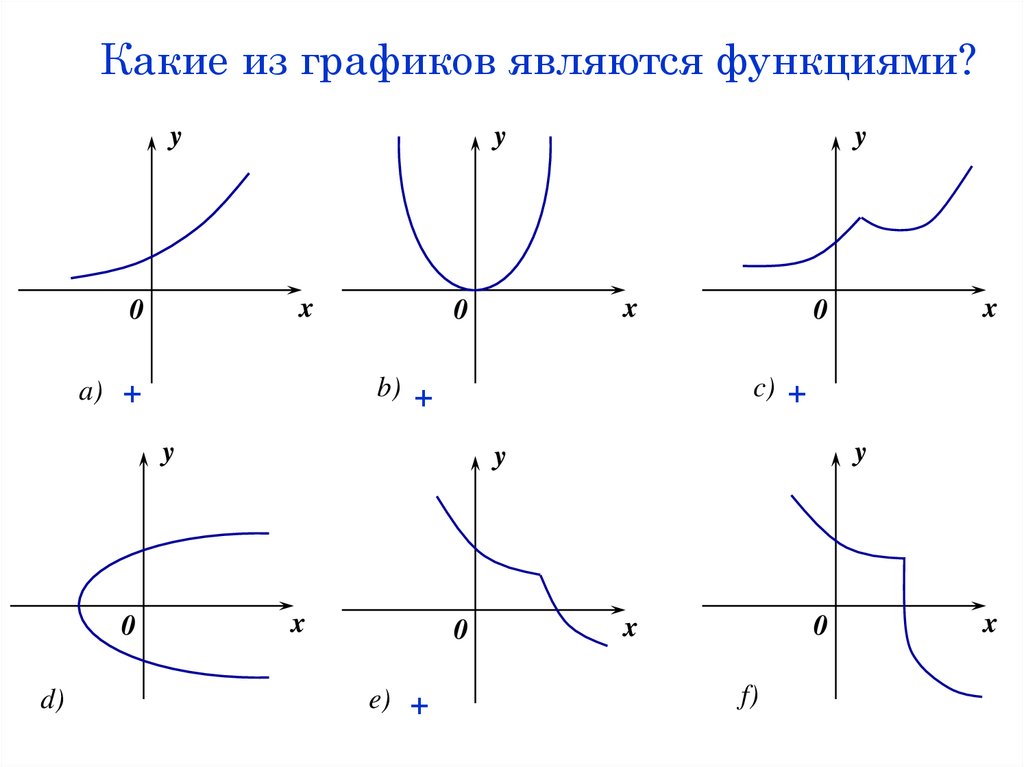
7. Какие из графиков являются функциями?
yy
x
0
y
y
x
0
e) +
x
0
c) +
y
d)
x
0
b) +
a) +
0
y
0
x
f)
x
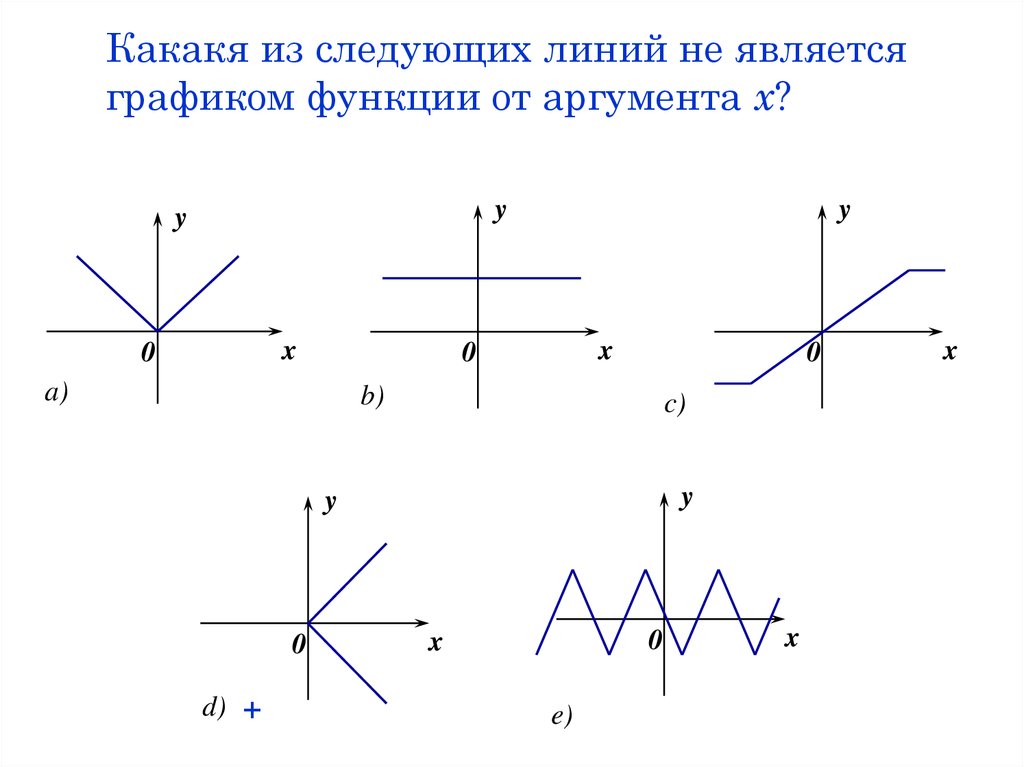
8. Какакя из следующих линий не является графиком функции от аргумента х?
yy
x
0
y
x
0
a)
0
b)
c)
y
y
0
d) +
0
x
e)
x
x
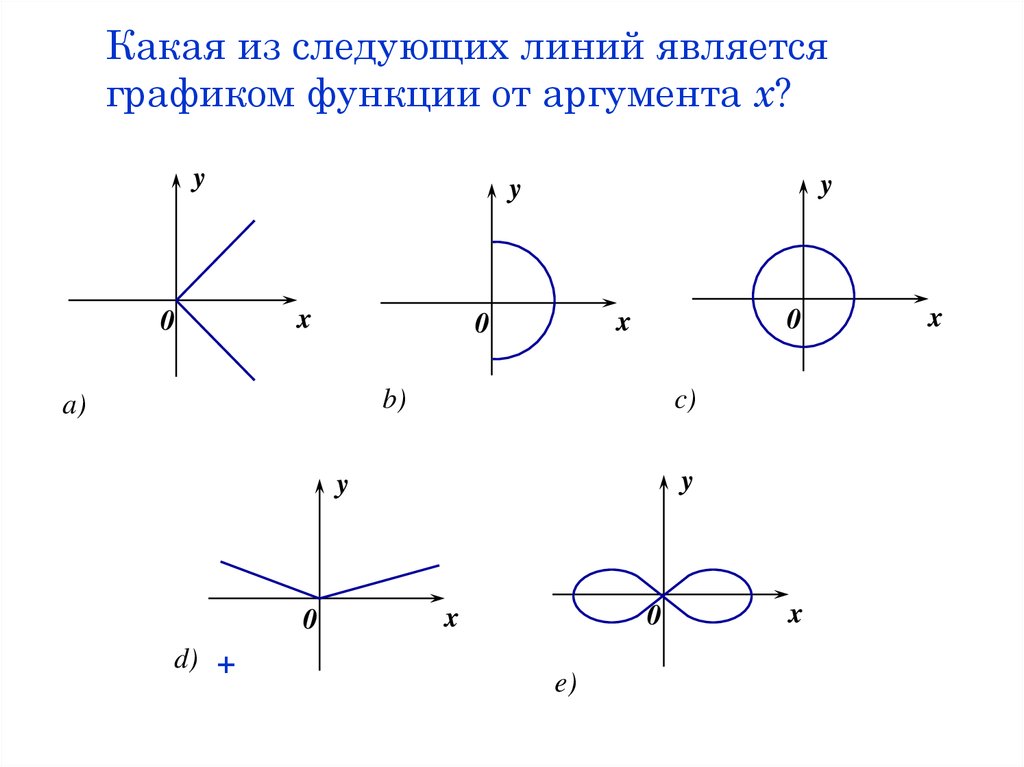
9. Какая из следующих линий является графиком функции от аргумента х?
y0
y
y
x
0
x
0
b)
a)
c)
y
y
0
d) +
0
x
e)
x
x
10.
• Областью определения функции y=f(x) называетсямножество
всех
действительных
значений
аргумента х.
y
y x
2
X ; R
y
0
y
0
1
y
x
x
x
X 0; R
x
X ; 0 0; R \ 0
y
0
x
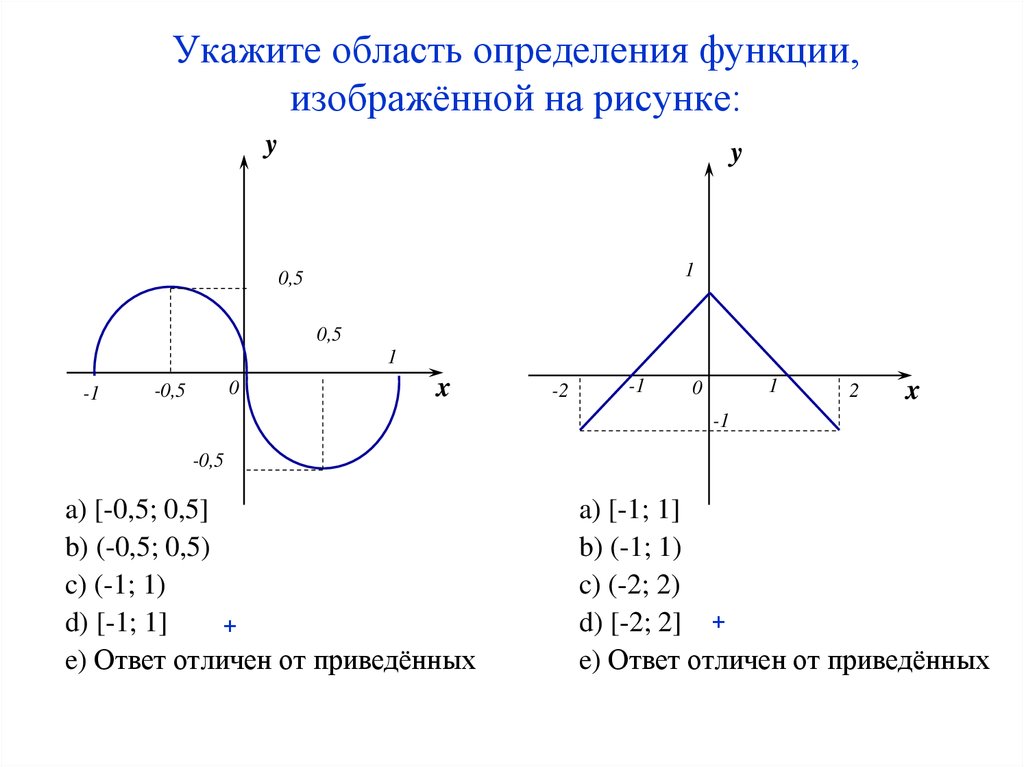
11. Укажите область определения функции, изображённой на рисунке:
yy
1
0,5
0,5
1
-1
0
-0,5
x
-2
-1
1
0
2
x
-1
-0,5
a) [-0,5; 0,5]
b) (-0,5; 0,5)
c) (-1; 1)
d) [-1; 1]
+
e) Ответ отличен от приведённых
a) [-1; 1]
b) (-1; 1)
c) (-2; 2)
d) [-2; 2] +
e) Ответ отличен от приведённых
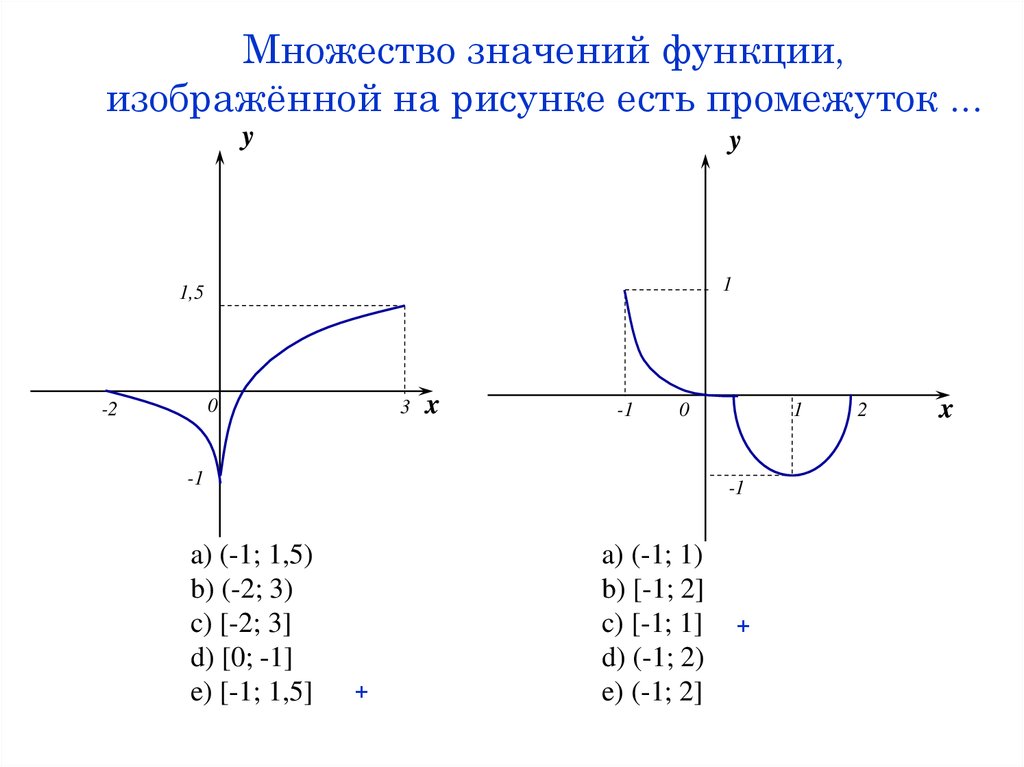
12. Множество значений функции, изображённой на рисунке есть промежуток ...
yy
1
1,5
0
-2
3
x
-1
0
-1
a) (-1; 1,5)
b) (-2; 3)
c) [-2; 3]
d) [0; -1]
e) [-1; 1,5]
1
-1
+
a) (-1; 1)
b) [-1; 2]
c) [-1; 1]
d) (-1; 2)
e) (-1; 2]
+
2
x
13. Особенности отыскания области определения некоторых функций
• 1). При отыскании области определениядробной функции нужно исключить
значения
аргумента,
при
которых
знаменатель обращается в ноль.
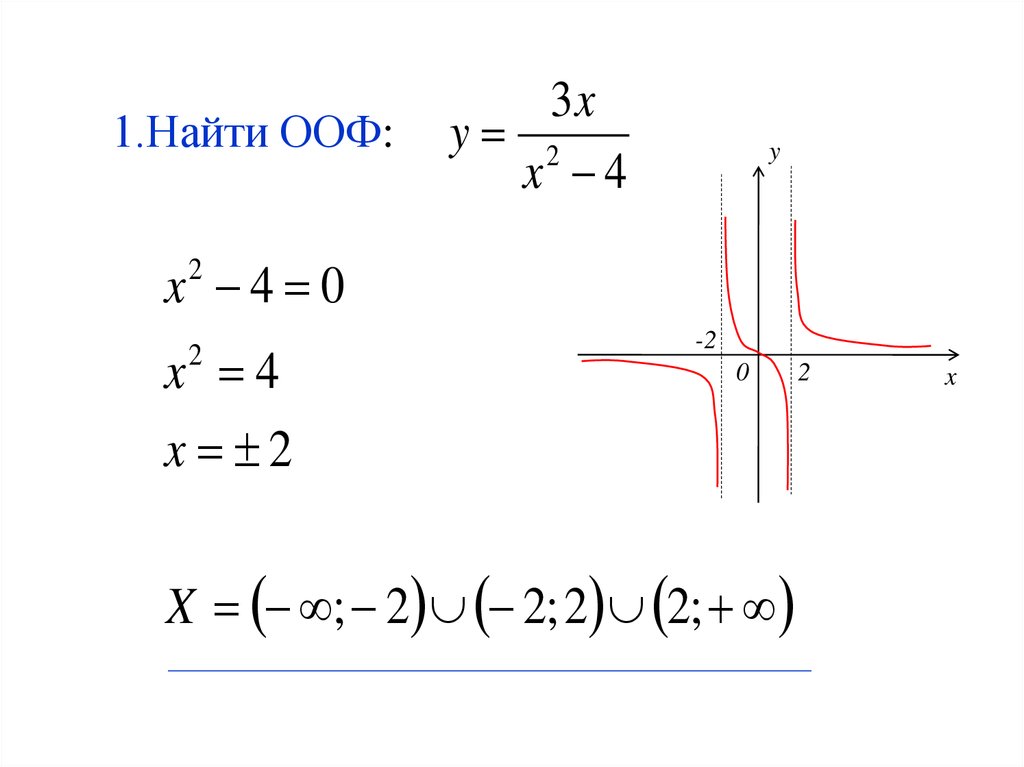
14. 1.Найти ООФ:
3xy 2
x 4
y
x 4 0
2
x 4
x 2
2
-2
0
X ; 2 2; 2 2;
2
x
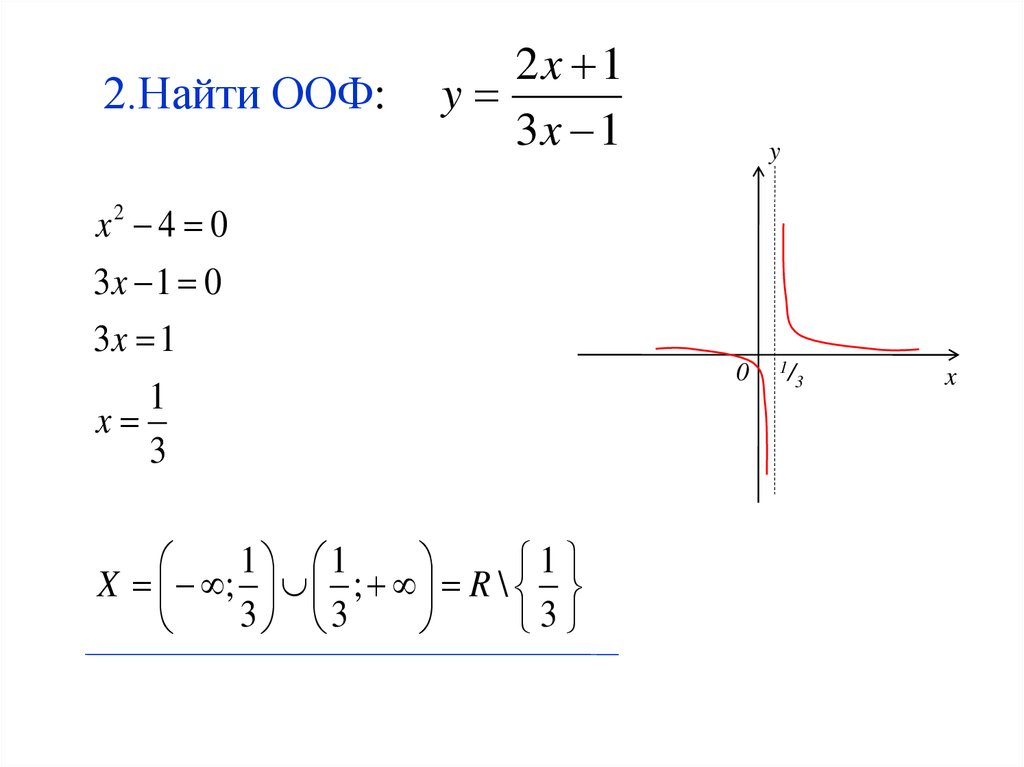
15. 2.Найти ООФ:
2x 1y
3x 1
y
x2 4 0
3x 1 0
3x 1
1
x
3
1 1
1
X ; ; R \
3 3
3
0
1/
3
x
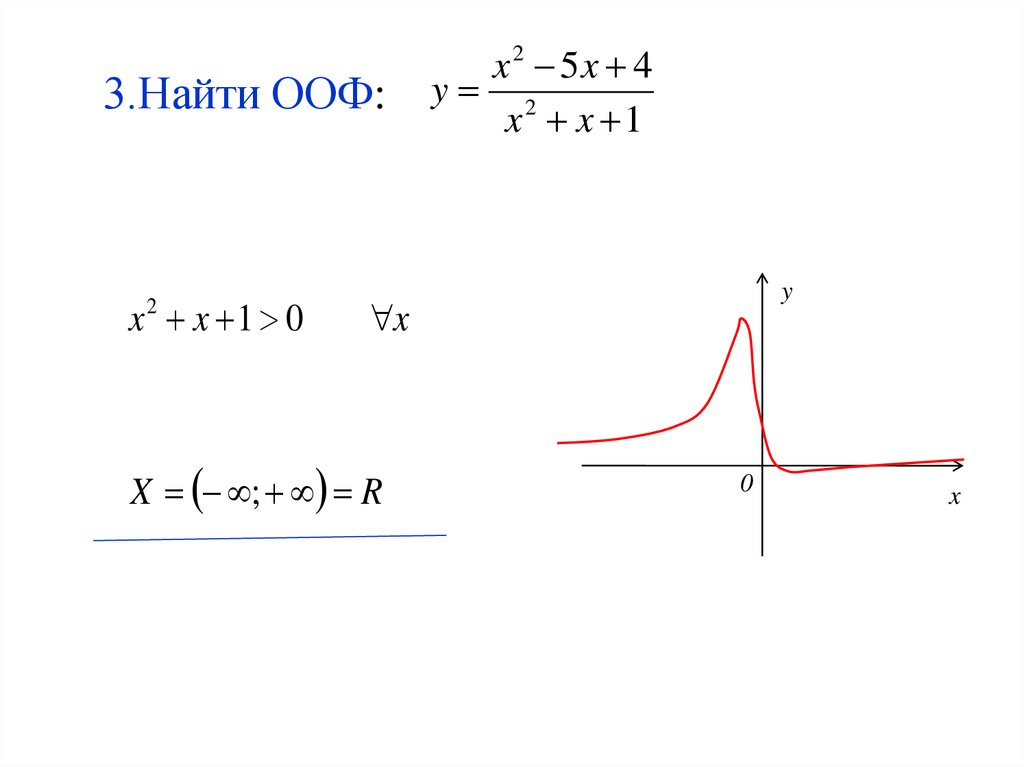
16. 3.Найти ООФ:
x x 1 02
x 2 5x 4
y 2
x x 1
y
x
X ; R
0
x
17.
• 2). Если аналитическое выражение функциисодержит корень четной степени, то при
отыскании
ООФ
нужно
исключить
значения
аргумента,
при
которых
подкоренное
выражение
принимает
отрицательное значение (т.е. подкоренное
выражение должно быть положительным).
18. Найти область определения функции:
пример 5пример 4
y x 3
x 3 0
y
y
-3
0
x
1
x 3
x 3 0
x 3
x 3
X - 3;
X - 3;
19. 6. Найти ООФ:
y x 42
6. Найти ООФ:
у
x 4 0
2
( x 2)( x 2) 0
0
-2
+
-2
+
2
X ; 2 2;
2
х
20. 7. Найти ООФ:
x xy
3x
2
7. Найти ООФ:
x2 x 0
x 0
x ( x 1) 0
x 0
X ; 0 1;
+
0
+
1
21.
• 3). Если аналитическое выражение функциисодержит логарифм, то при отыскании
ООФ
нужно
исключить
значения
аргумента, при которых выражение под
знаком
логарифма
принимает
отрицательное значение и обращается в
ноль (т.е. выражение под знаком логарифма
должно быть строго положительным).
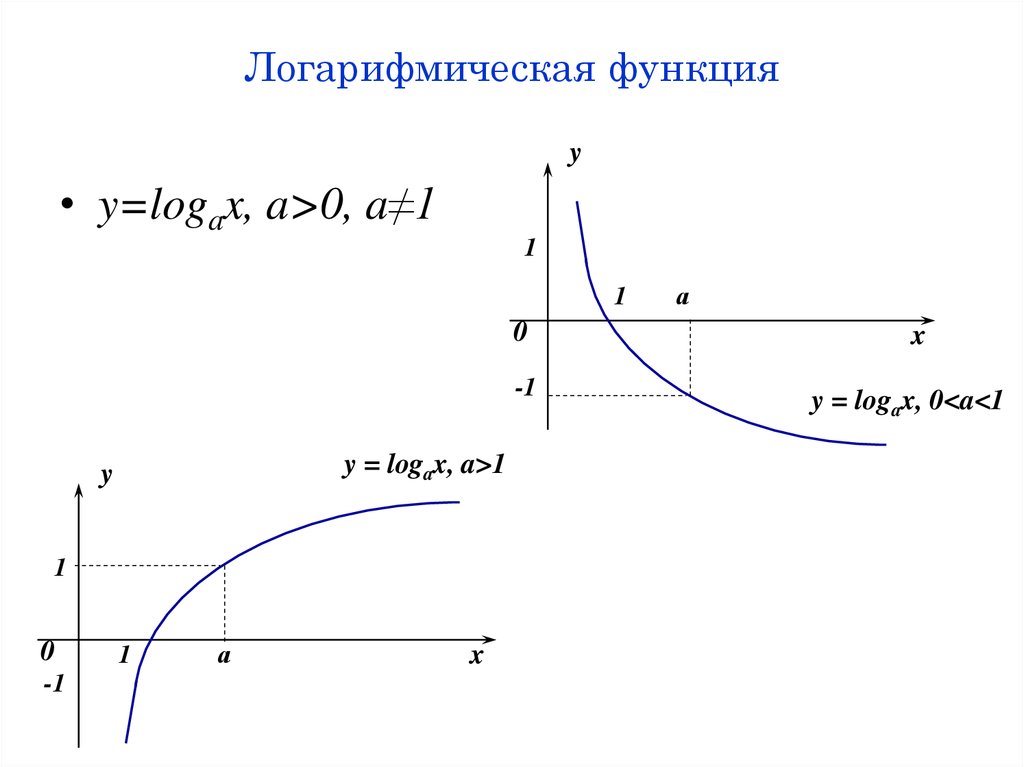
22. Логарифмическая функция
y• y=logax, a>0, a≠1
1
1
0
-1
y = logax, a>1
y
1
0
-1
1
а
x
а
x
y = logax, 0<a<1
23. Найти ООФ:
пример 8y log( x 2)
x 2 0
x 2
X 2;
пример 9
3
y log
17 x
3
0
17 x
17 x 0
x 17
x 17
X - ;17
24. 10. Найти ООФ:
y log 3 x 2 9x2 9 0
( x 3)( x 3) 0
+
-3
+
3
X ; 3 3;
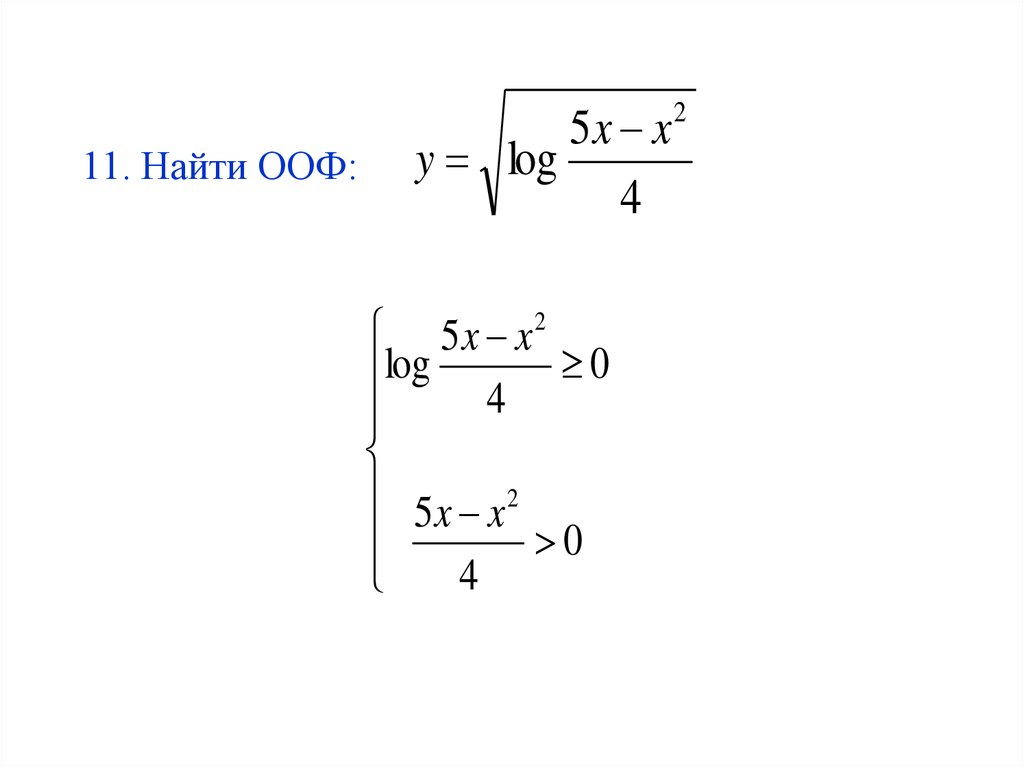
25. 11. Найти ООФ:
5x xy log
4
5x x 2
0
log
4
5x x 2
0
4
2
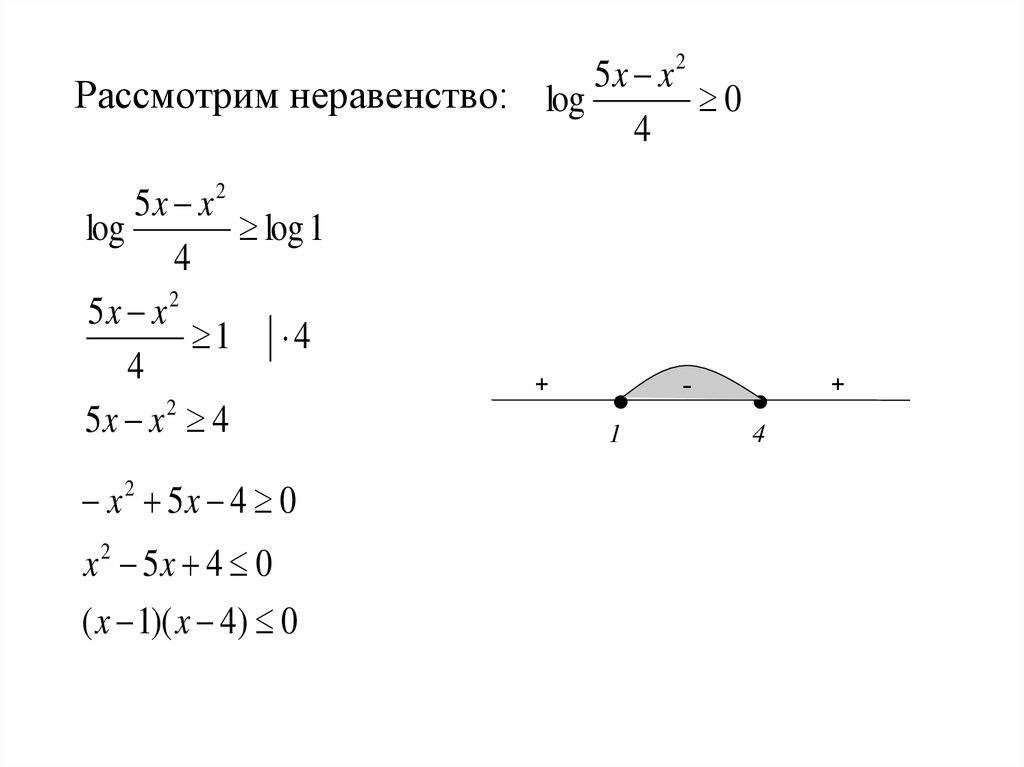
26. Рассмотрим неравенство:
5x x 2Рассмотрим неравенство: log
0
4
5x x 2
log
log 1
4
2
5x x
1 4
4
2
5x x 4
x2 5x 4 0
x 2 5x 4 0
( x 1)( x 4) 0
+
1
+
4
27. Рассмотрим неравенство:
5x x 20
4
Рассмотрим неравенство:
5x x 2
0
4
5x x 2 0
x (5 x) 0
4
-
-+
0
5
Рассмотрим оба решения на одной прямой:
1
0
4
5
X 1; 4
28.
• 4). Если аналитическое выражение функциисодержит обратные тригонометрические
функции arcsin и arccos, то при отыскании
ООФ нужно включать только те значения
аргумента, при которых
выражения,
стоящие под знаком этих функций , по
модулю не превосходят единицы.
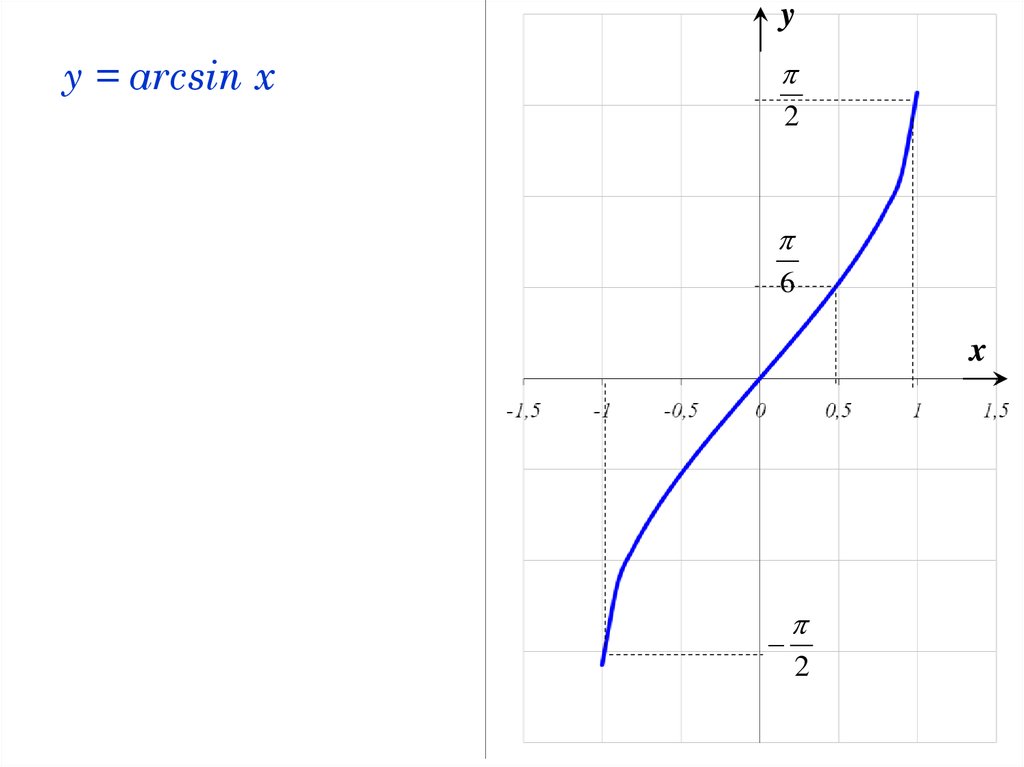
29. y = arcsin x
yy = arcsin x
2
6
x
2
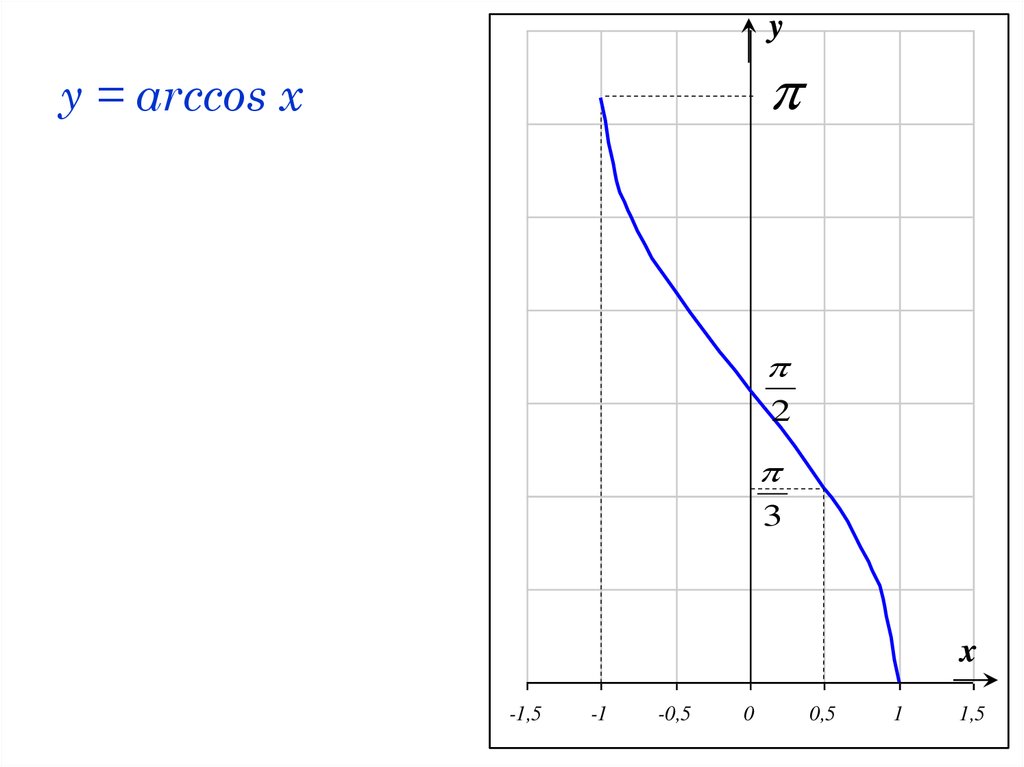
30. y = arccos x
yy = arccos x
2
3
x
-1,5
-1
-0,5
0
0,5
1
1,5
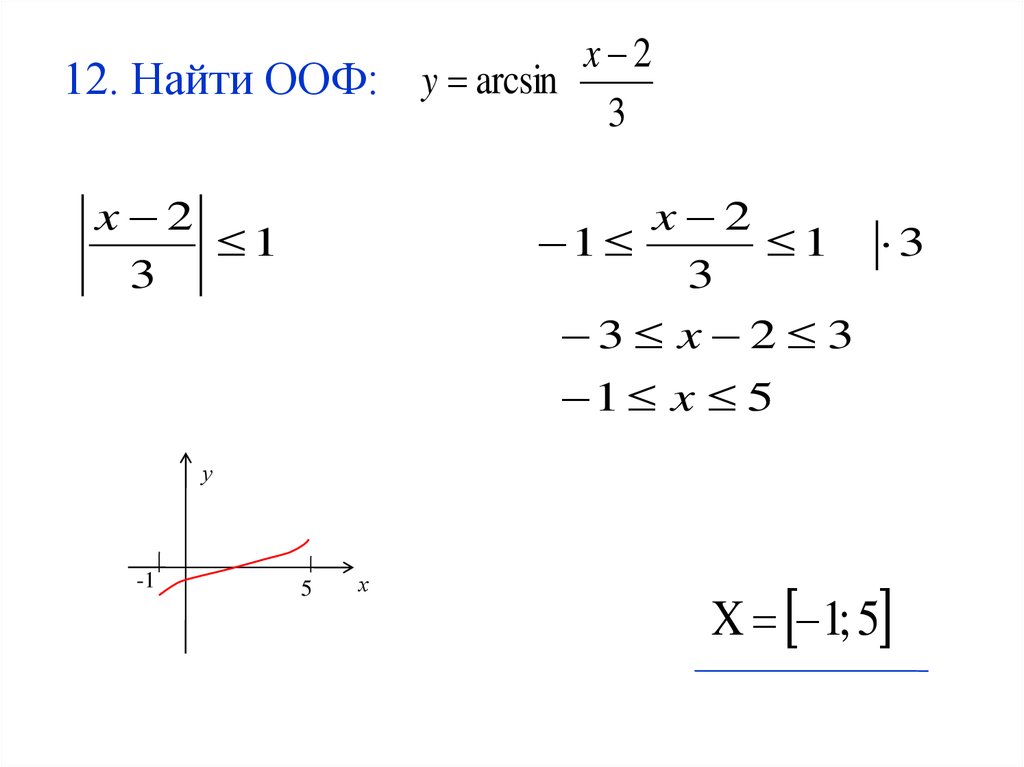
31. 12. Найти ООФ:
x 212. Найти ООФ: y arcsin
3
x 2
1
3
x 2
1
1 3
3
3 x 2 3
1 x 5
у
-1
5
х
X 1; 5
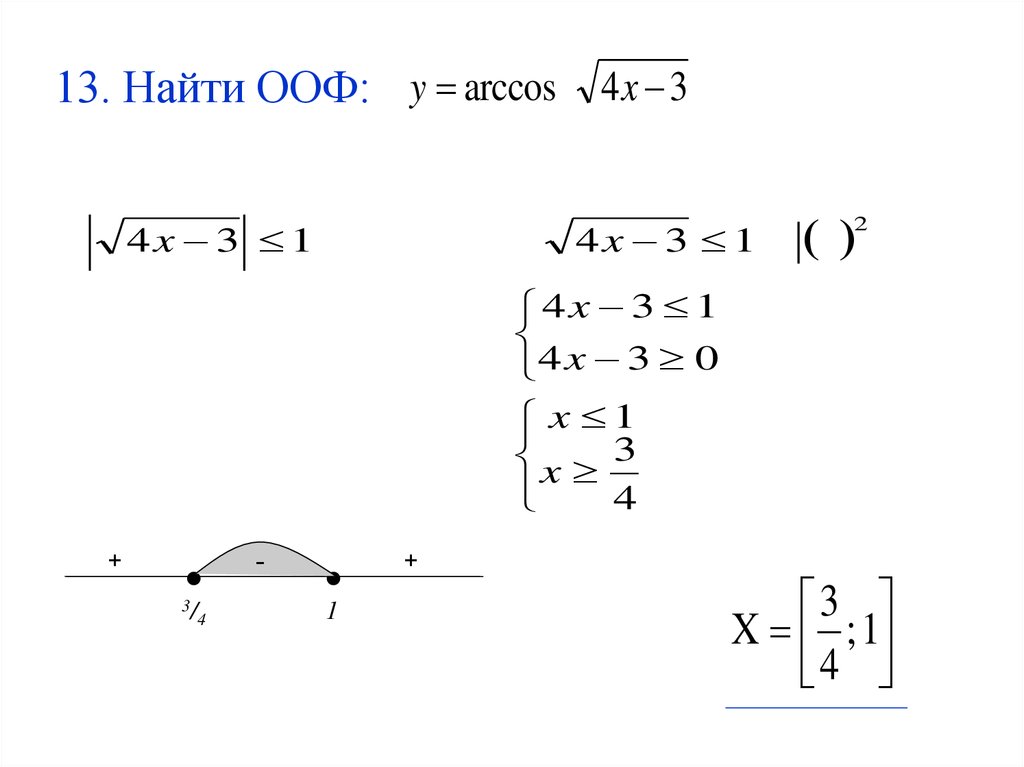
32. 13. Найти ООФ:
y arccos 4 x 34x 3 1
4x 3 1
2
4x 3 1
4 x 3 0
x 1
x 3
4
+
3/
4
+
1
3
X ; 1
4
33. 2. Способы задания функции
• аналитический способ (функция задается припомощи некоторой формулы)
y log x
2
• табличный способ
x
1/8
1/4
1/2
1
2
4
8
y
-3
-2
-1
0
1
2
3
y
• графический способ
0
1
x
34.
Иногда рассматривают функции, которые наразличных участках изменения х задаются
разными аналитическими формулами:
x3 ,
x 0
y f ( x) x 1, 0 x 2
3,
2 x 4
у
3
1
X ; 4
Y ; 0 1; 3
0
2
x















 Математика
Математика








