Случайные события

1. Случайные события

1) Интуитивное представление о вероятности
2) Пространство элементарных событий
3) Алгебра событий
4) Вероятностное пространство
5) Свойства вероятностей
6) Повторение испытаний
1

2. Интуитивное представление о вероятности

1) Априорный подход
(a priori – до опыта)
Классическое определение вероятности события А
m
P А
n
Принцип равных возможностей
n - общее количество случаев
m - количество благоприятных
случаев
2) Апостериорный подход (a posteriori – после опыта)
Статистическое определение вероятности события А
m
P А lim
n n
n - общее количество опытов
m - количество опытов, в которых
наблюдалось событие А
2

3. Пространство элементарных событий

Неопределяемые понятия
Вероятностный эксперимент (опыт)
Элементарное событие (исход опыта)
Вероятность элементарного события
Основные определяемые понятия и обозначения
Пространство элементарных событий
А
Случайное событие А
А 1 , 2 , ..., k
Благоприятные исходы
0 и 1 U Невозможное и достоверное события
3

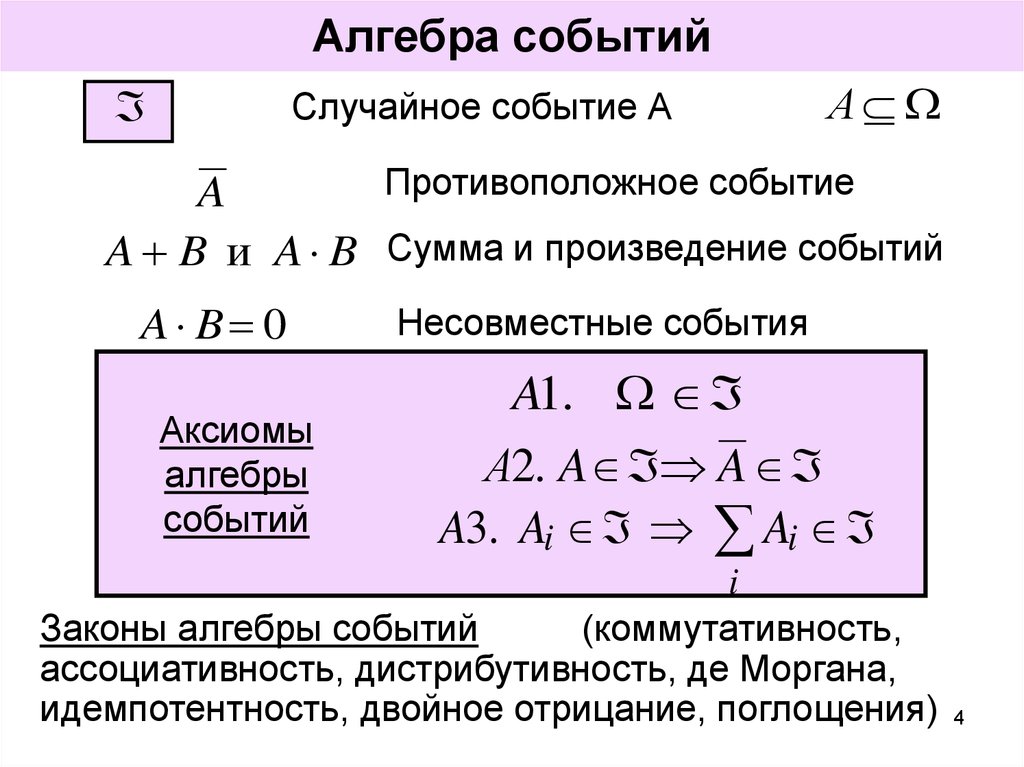
4. Алгебра событий

Случайное событие А
А
Противоположное событие
A
A B и A B Сумма и произведение событий
A B 0
Аксиомы
алгебры
событий
Несовместные события
A1.
А2. A A
A3. Ai Ai
i
Законы алгебры событий
(коммутативность,
ассоциативность, дистрибутивность, де Моргана,
идемпотентность, двойное отрицание, поглощения)
4

5. Вероятностное пространство

Р(А)
Пространство элементарных событий
Алгебра событий
Вероятность события А
Р : 0;1
Р – Неотрицательная аддитивная вероятностная мера
A4. P A 0;
Аксиомы
вероятности
A6.
A5. P 1
Ai A j 0 i j
P Ai P Ai
i
i
Вероятностное пространство
, , Р
5

6. Классическое вероятностное пространство

, , Р
1) Пространство элементарных событий конечно
Все исходы равновозможны
n
2) Алгебра событий – все подмножества Ω
А 1 , 2 ,..., m
3) Классическое определение вероятности события А
m
P А
n
n - общее количество исходов
m - количество благоприятных
исходов
6

7. Геометрическое вероятностное пространство

, , Р
1) Пространство элементарных событий несчетно
Все исходы равновозможны
2) Алгебра событий – все измеримые подмножества Ω
А
измеримое множество
3) Геометрическое определение вероятности
мера А
P А
мера
мера – неотрицательная
аддитивная функция
(длина отрезка,
площадь фигуры,
объем тела)
7

8. Свойства вероятностей

1
2
3
P 0
A6
A5
1 P
P 1
P P 1 1 P P 0
P A 1 P A
A6
P P A A P A P A
1 P A P A P A 1 P A
A B P A P B
A6
B A B A
P B P A P B A
A4
P A P B
8

9. Свойства вероятностей

4
Теорема сложения
P A B P A P B P A B
B B A B A
A A B A B
P B P B A P B A
P A P A B P A B
P A P B P A B 2P A B P A B
(1)
A B A B A B B A
P A B P A B P A B P B A
(2)
9

10. Свойства вероятностей

5
Теорема умножения
P A B P A P B A P B P A B
P A B
P A B
,
P B
P B 0
Условная
вероятность
P A B P A
Независимые события
Критерий независимости
A и B независимы
P A B P A P B
События, независимые в совокупности
10