Случайные события. Вероятностное пространство

1. Случайные события

Вероятностное пространство
A1.
A4. P A 0;
А2. A A
A6.
A3. Ai
Ai
i
n
m
P А
n
, , Р
A5. P 1
Ai A j 0 i j
P Ai P Ai
i
i
Все исходы равновозможны
мера А
P А
мера
1

2. Случайные события

3
Случайные события
Свойства вероятностей
P 0
P A 1 P A
A B P A P B
4
P A B P A P B P A B
1
2
5
Теорема умножения
P A B P A P B A P B P A B
P A B
P A B
,
P B
P B 0
2

3. Свойства вероятностей

5
P A B P A P B A P B P A B
P A B
P A B
,
P B
P B 0
Пример. 20 вопросов из 25 выучил. Последовательно
2 вопроса. Р(ответит на оба)=?
19
20
5
25
25
24
++
4
24
+-
-+
--
20 19
P A B P A P B A 0,63
25 24
3

4. Свойства вероятностей

Определение. A и B независимы
6
Теорема (критерий независимости)
A и B независимы
7
P A B P A
P A B P A P B
События А1 , A2 , ..., An независимы
в совокупности
набора
Аk 1 , Ak 2 ,..., A kr
1 k1 k r n
P Аk1 Ak 2 ... A kr P Аk1 P Ak 2 ... P A kr
4

5. Свойства вероятностей

Пример. Опыт – бросание двух монет. Событие A –
герб на первой, B – герб на второй монете, С – ровно
один герб. Независимы ли события А, В, С?
РР, РГ , ГР, ГГ
P AB P A P B
P ВС P В P С
P AС P A P С
P A P В P С 0,5
P AB P AС P ВС 0,25
- A, B, С независимы попарно
P A P B P B 0,125
P ABС 0
- А, В, С
зависимы
P АВС P А P В P С
в совокупности
НС НП
НП НС
5

6. Свойства вероятностей

8
Пусть
Теорема о полной вероятности
H i H i 0 i j
Hi
i
P A P H i P A H i
i
Доказательство
H1 H 2 ... H n
( A6)
A A H1 A H 2 ... A H n
(ТУ )
P A P A H1 P A H 2 ... P A H n
P A P H i P A H i
i
6

7. Свойства вероятностей

Теорема Байеса
Пусть
H i H i 0 i j
9
Hi
i
P H k P A H k
P H k A
P H i P A H i
i
Доказательство
P A P H k A
P A H k P H k P A H k
P H k P A H k
P H k A
P A
7

8. Свойства вероятностей

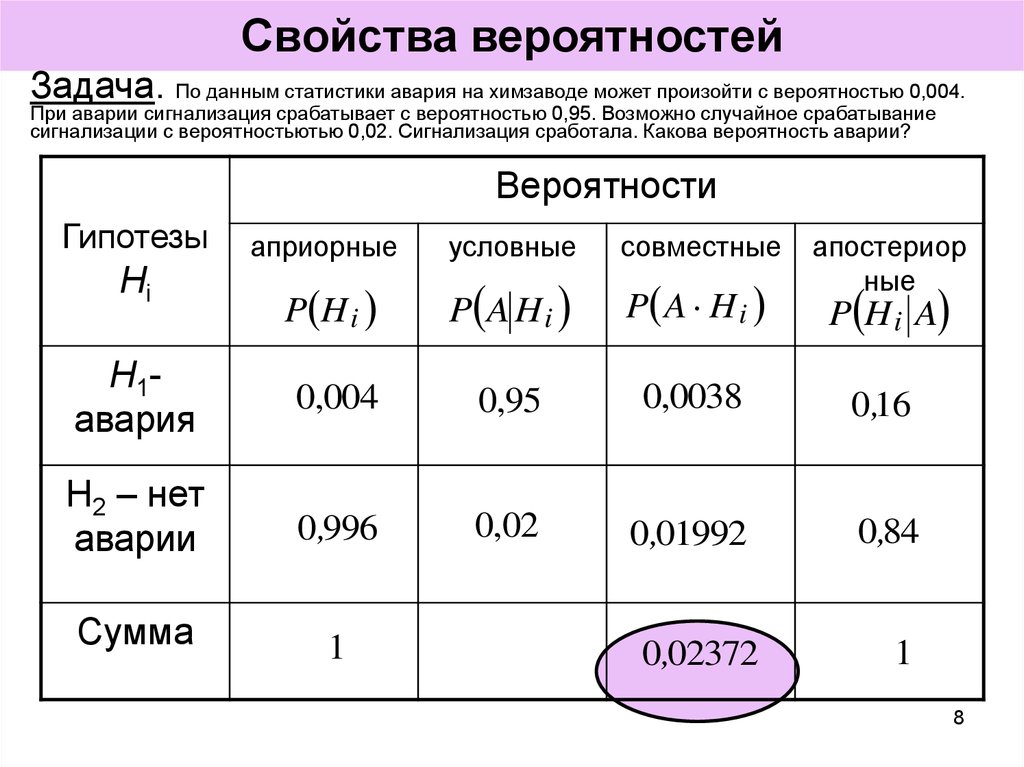
Задача. По данным статистики авария на химзаводе может произойти с вероятностью 0,004.
При аварии сигнализация срабатывает с вероятностью 0,95. Возможно случайное срабатывание
сигнализации с вероятностьютью 0,02. Сигнализация сработала. Какова вероятность аварии?
Вероятности
Гипотезы
априорные
условные
совместные
Hi
P H i
P A H i
P A H i
апостериор
ные
P Hi A
H1авария
0,004
0,95
0,0038
0,16
H2 – нет
аварии
0,996
0,02
0,01992
0,84
Сумма
1
0,02372
1
8

9. Повторение испытаний

Схема испытаний Бернулли
1) Проводится n независимых опытов
2) В каждом опыте – У или Н (У∙Н=0, У+Н=Ω)
3) Р(У)=р, Р(Н)=q (р+q=1)
Вероятность наблюдать k успехов в схеме n
испытаний Бернулли
Pn k
k k n k
Cn p q
Производящая функция
Наивероятнейшее число
успехов k*
0 k n
z pz q n
np q k * np p
9

10. Повторение испытаний

Пример Тест: 5 вопросов, по 3 ответа в каждом.
Какова вероятность угадать 4?
Pn k Cnk p k q n k
4 1
P5 4 C5
3
4
n 5
1
2
3
Производящая функция
z
1
p
3
5! 1
4! 1! 3
4
2
q
3
k 4
1
2 10
0.04
3 243
z
1
243
z 2
5
z 5 10 z 4 40 z 3 80 z 2 80 z1 32
243
1
Наивероятнейшее
число успехов k*
*
k1 np q 1
*
k 2 np p 2
10

11. Повторение испытаний

Динамическая модель (обобщение схемы Бернулли)
1) Проводится n независимых опытов
2) В каждом опыте – У или Н (У∙Н=0, У+Н=Ω)
3) Р(Уk)=рk, Р(Нk)=qk (рk+qk=1)
Производящая функция
n
z pk z qk
k 1
Вероятность наблюдать k успехов в n опытах
динамической модели равна коэффициенту при zk
11

12. Повторение испытаний

Пример
Тест: 5 вопросов, в первом и во втором
по 3 ответа, в третьем и четвертом – по 5, в пятом - 2.
Какова вероятность угадать 4 верных ответа?
1
1
1
n 5 p1 p2
p3 p4
p5
3
5
2
2
2
Производящая
1
z z
3
функция
z
1
9 25 2
4 1
1
z z
3 5
5 2
2
z 2 2 z 4 2 z 1
2 1
z 2 4 z 4 z 2 8 z 16 z 1
450
1
1
z 5 13z 4 64 z 3 158 z 2 160 z1 64
450
P5 4
13
450
0.029
12

13. Повторение испытаний

Полиномиальная модель (обобщение схемы Бернулли)
1) Проводится n независимых опытов
2) В каждом опыте – m взаимоисключающих
исходов А1, А2,…, Аm (полная группа)
3) Р(А1)=р1, Р(А2)=р2,…, Р(Аm)=рm (р1+p2+…+pm=1)
Вероятность наблюдать k1 раз исход А1,
k2 раз исход А2, …, km раз исход Аm
в серии n опытов равна
n!
k1
k2
km
Pn k1 ,k 2 ,...,k m
p1 p2 ... pm
k1! k 2! ... k m !
Производя
щая
функция
z1 , z2,...,zm p1z1 p2 z2 ... pm zm
n
13