Метод наименьших квадратов. Уравнение парной регрессии. (Лекция 6 по эконометрике)

1.

Лекция 6
Метод наименьших квадратов
Уравнение парной регрессии
1

2.

В математической статистике методы получения
наилучшего приближения к исходным данным в виде
аппроксимирующей функции получили название
регрессионного анализа
Основными задачами регрессионного анализа являются
установление зависимости между переменными и оценка
(прогноз) значений зависимой переменной
В экономических исследованиях часто заданному
значению одной переменной может соответствовать
множество значений другой переменной
Другими словами, каждому значению одной переменной
соответствует условное распределение другой переменной
2

3.

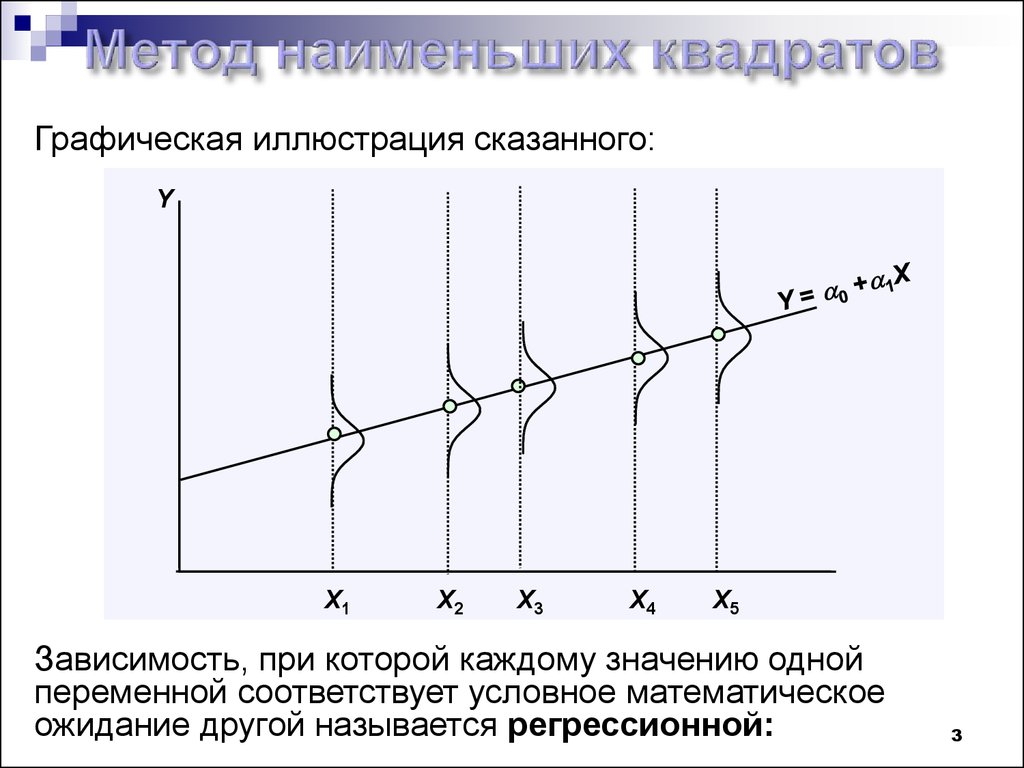
Графическая иллюстрация сказанного:
Y
X1
X2
X3
X4
X5
Зависимость, при которой каждому значению одной
переменной соответствует условное математическое
ожидание другой называется регрессионной:
3

4.

Начнем с построения модели в виде линейного уравнения
парной регрессии
yt a0 a1 xt ut
(6.1)
Постановка задачи
Дано:
Выборка наблюдений за поведением переменных yt и xt
Найти:
1. Оценки значений параметров a0 и a1
2. Оценки точности σ(a0) и σ(a1).
3. Оценка рассеяния случайного возмущения σu
4. Оценку точности прогнозирования σ(y(x0))
4

5.

Введем следующие обозначения и определения
1. Выборка
y1
y2
...
yn
x1
x2
...
xn
2. Система уравнений
наблюдений
y1 a0 a1 x1 u1
y 2 a0 a1 x 2 u2
.......... .......... ....
y
n a0 a1 xn un
3. В е к т о р а
y1
y
Y 2
...
yn
x1
X x 2
...
xn
u1
U u2 a a0
...
a1
un
(6.2)
4. Матрица
коэффициентов
при параметрах
1
1
X
...
1
x1
x2
...
xn
5

6.

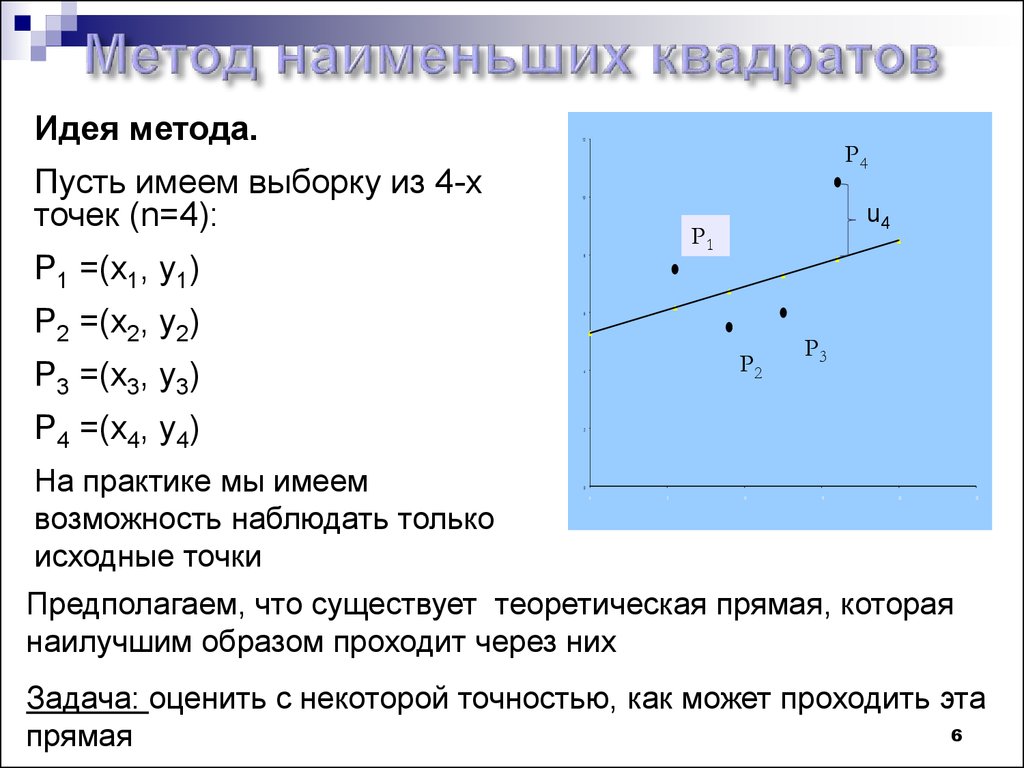
Идея метода.
Пусть имеем выборку из 4-х
точек (n=4):
P1 =(x1, y1)
P2 =(x2, y2)
P3 =(x3, y3)
P4 =(x4, y4)
На практике мы имеем
возможность наблюдать только
исходные точки
12
P4
10
u4
P1
8
6
P2
4
P3
2
0
0
5
10
15
20
25
Предполагаем, что существует теоретическая прямая, которая
наилучшим образом проходит через них
Задача: оценить с некоторой точностью, как может проходить эта
6
прямая

7.

Итак, оценки параметров модели парной регрессии
согласно МНК будем искать из условия:
n
S u
2
i
i 1
yi ~
a0 ~
a1 xi min
2
(6.2)
Условиями минимума функции являются равенство нулю
первых производных и положительность вторых
производных по ã0 и ã1
S
~
2 yi ~
a
0 a1 xi 1 0
~
a0
S
~
2 yi ~
a
0 a1 xi xi 0
~
a1
(6.3)
Система (6.3) называется системой нормальных
уравнений для вычисления оценок параметров уравнения
7
парной регрессии (6.1)

8.

Упростим систему нормальных уравнений (6.3)
n ~
a0 ~
a1 xi yi
2
~
~
xi a0 a1 xi xi yi
(6.4)
Убеждаемся, что решение системы уравнений (6.4) будет
соответствовать минимуму функции (6.1)
Для этого вычисляем значения вторых частных
производных функции (6.1)
2
S n 0
2
~
a0
2
S
2
~
a1
x
2
i
0
Вторые производные больше
нуля – функция (6.1)
принимает минимальное
значение в точке ã0 , ã1
8

9.

n ~
a0 ~
a1 xi yi
2
~
~
xi a0 a1 xi xi yi
(6.4)
Для решения системы (6.4) выразим из первого
уравнения ã0, подставим его во второе уравнение
1
~
a0 yi ~
a1 xi
n
(6.5)
1
2
~
y
xi n i a1 xi xi a1 xi yi
Решив второе уравнение системы (6.5) получим:
~
a1
n xi yi xi yi
n x x x
2
i
i
i
(6.6)
9

10.

~
a1
n xi yi xi yi
n xi2 xi xi
(6.6)
Проанализируем выражение (6.6)
Для этого вычислим COV(x,y) и σ2(x)
1
1
xi x yi y
xi yi x yi xi y xy
Cov( x, y )
n 1
n 1
1
n xi yi xi yi
n n 1
( x)
2
2
1
1
1
2
2
2
x
(
2
x
)
n
xi xi
x
x
x
x
x
i
i
i
i
n 1
(n 1)
n n 1
Cov( x, y )
~
a1
2
( x)
(6.7)
10

11.

Проверим выполнение условия несмещенности для
оценки (6.7)
Для этого вычислим числитель выражения (6.7)
Cov( x, y ) Cov( x, a0 a1 x u)
Cov( x, a0 ) Cov( x, a1 x ) Cov( x,u)
Подставив в (6.7) полученное выражение получим:
Cov( x, u)
~
a1 a1
2
( x)
(6.8)
Математическое ожидание выражения (6.7) имеет вид:
1
(6.9)
~
M(a1) a1 2 Cov( x,u)
( x)
11

12.

Вычислим дисперсии параметров уравнения регрессии и
дисперсию прогнозирования эндогенной переменной
1. Дисперсия параметра ã1
1
x
(
y
)
y
xi
i
Cov
(
x
,
y
)
2
(n 1)
2 ~
2
(
)
a1
2
2
1
(
x
)
x
(n 1) xi
xi x ( y a0 a1 x )
xi x ui
i
2
2
2
2
x
x
xi
xi
(~
a1)
2
( xi x )2 2 (ui )
x x
2 2
i
1
n 2 ( x )
2
u
(6.10)
12

13.

2. Дисперсия параметра ã0
1
~
a0 yi ~
a1 xi y ~
a1 x
n
~
a y ~
a x ( y ) x (~
a ) 2xCov y, ~
a
~
a ( y ) x (~
a)
2
2
2
0
2
2
2
1
2
1
2
0
1
2
1
σ2(y) Определяется с помощью (6.10)
2
(u)
1
1
2
2
2
( y ) yi 2 a0 a1 xi ui
n
n
n
В результате получаем:
2 ~
a0
2
1
x
2
(u) 2
n n ( x)
13

14.

Исходные предположения
1. Уравнение имеет вид: yt=a0 + a1xt + ut
2. Случайное возмущение имеет нормальное
распределение с параметрами 0 и σu
3. Для получения ММП-оценок имеем выборку из n
наблюдений
Тогда:
ut yt a0 a1 xt
Закон распределения для случайного возмущения
принимает вид:
2
y
t
0
1
0
a
a
x
1
t
exp
pu ut a0 , a1
12
2
2
u
2 u
14

15.

1. Функция правдоподобия получит вид:
2
2
y a a x
y
t n
a
0
1 t
0 a1x t 0
t
1
t
1
2
2
L ut a0 , a1
2
2
1
n
u
u
e
e
t 1
2 2 u
2 2 nu
2. Логарифм функции правдоподобия
1
1 y t a0 a1 xt
ln L ut a0 , a1 ln
ln n
n
2
u
2 2
2 u
2
15

16.

3. Составляем уравнения для вычисления оценок a0 и a1
ln L
yi n a0 a1 xi 0
a0
ln L
xt yt xt a0 a1 x2t 0
a1
Получили систему уравнений совпадающую с (6.3)
Следовательно, и решения совпадут
16

17.

Вывод
С помощью метода наименьших квадратов получили
1. Оценки параметров уравнения регрессии, по крайней
мере, состоятельными
2. Если случайное возмущение подчиняется
нормальному закону распределения, то оценки
параметров модели несмещенные и эффективные
3. Нет необходимости в знании закона распределения
случайных возмущений
17

18.

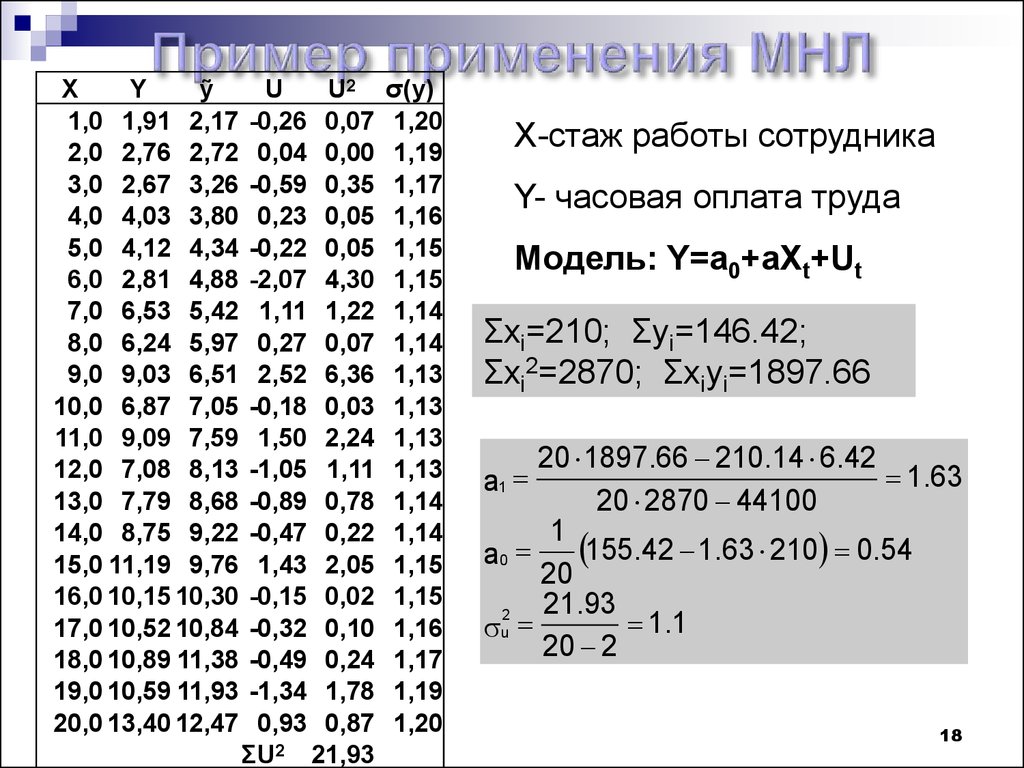
X
Y
ỹ
1,0 1,91 2,17
2,0 2,76 2,72
3,0 2,67 3,26
4,0 4,03 3,80
5,0 4,12 4,34
6,0 2,81 4,88
7,0 6,53 5,42
8,0 6,24 5,97
9,0 9,03 6,51
10,0 6,87 7,05
11,0 9,09 7,59
12,0 7,08 8,13
13,0 7,79 8,68
14,0 8,75 9,22
15,0 11,19 9,76
16,0 10,15 10,30
17,0 10,52 10,84
18,0 10,89 11,38
19,0 10,59 11,93
20,0 13,40 12,47
U
U2
-0,26 0,07
0,04 0,00
-0,59 0,35
0,23 0,05
-0,22 0,05
-2,07 4,30
1,11 1,22
0,27 0,07
2,52 6,36
-0,18 0,03
1,50 2,24
-1,05 1,11
-0,89 0,78
-0,47 0,22
1,43 2,05
-0,15 0,02
-0,32 0,10
-0,49 0,24
-1,34 1,78
0,93 0,87
ΣU2 21,93
σ(y)
1,20
1,19
1,17
1,16
1,15
1,15
1,14
1,14
1,13
1,13
1,13
1,13
1,14
1,14
1,15
1,15
1,16
1,17
1,19
1,20
X-стаж работы сотрудника
Y- часовая оплата труда
Модель: Y=a0+aXt+Ut
Σxi=210; Σyi=146.42;
Σxi2=2870; Σxiyi=1897.66
20 1897.66 210.14 6.42
1.63
20 2870 44100
1
155.42 1.63 210 0.54
a0
20
21.93
2
1 .1
u
20 2
a1
18

19.

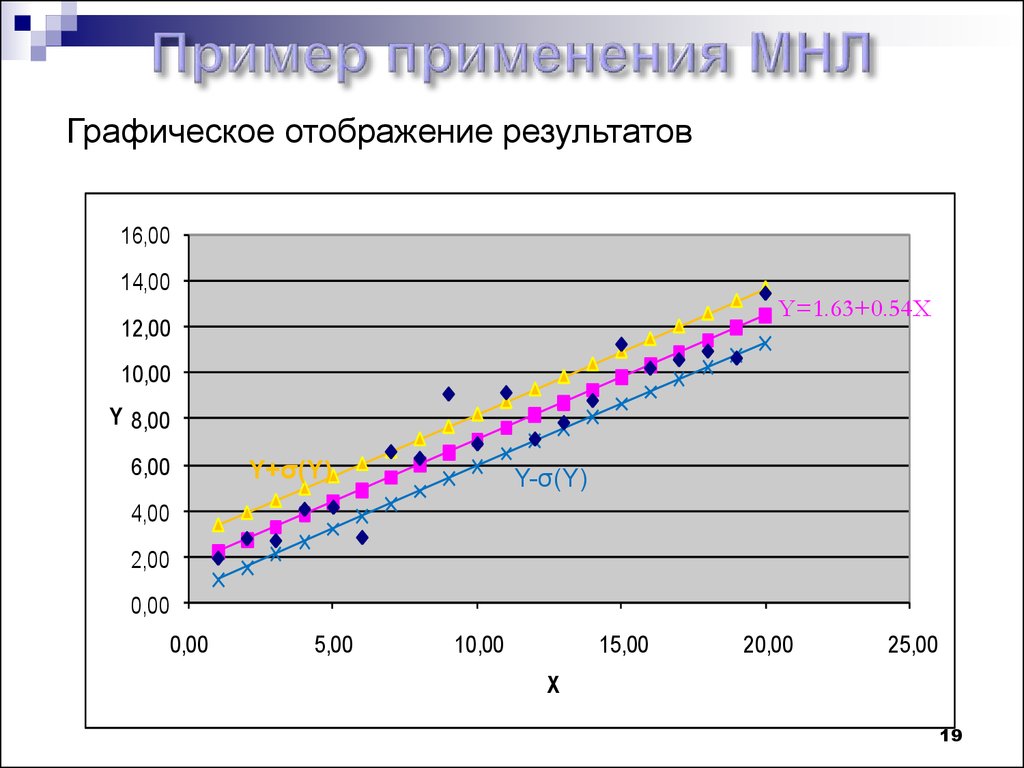
Графическое отображение результатов
16,00
14,00
Y=1.63+0.54X
12,00
10,00
Y 8,00
6,00
Y+σ(Y)
Y-σ(Y)
4,00
2,00
0,00
0,00
5,00
10,00
15,00
20,00
25,00
X
19

20.

Выводы:
1. Метод наименьших квадратов имеет следующие
преимущества:
- не требуется знания закона распределения
случайного возмущения
- дает оценки по крайней мере состоятельные
- в случае нормального распределения случайного
возмущения оценки параметров линейной модели
несмещенные и эффективные
2. Для получения несмещенных и эффективных
оценок параметров в случае, если случайное возмущение
имеет закон распределения отличный от нормального,
необходимо наложить на него дополнительные
требования
20