Похожие презентации:
Обобщенная модель множественной регрессии
1. Лекция 4 Обобщенная модель множественной регрессии
1. Мультиколлинеарность2. Гетероскедастичность
2.
1. МультиколлинеарностьПод мультиколлинеарностью понимают
высокую взаимную коррелированность
объясняющих переменных.
Мультиколлинеарность может
проявляться в функциональной и
стохастической формах.
3.
В первом случае, по крайней мере, однапара из объясняющих переменных связана
линейной функциональной зависимостью
и тогда говорят о строгой
мультиколлинеарности этих факторов. В
этом случае в матрице X в силу линейной
зависимости двух её столбцов нарушается
предпосылка 6° МНК – ранг матрицы X
будет меньше, чем p 1 .
4.
В этом случае матрица X X будетвырожденной и обратной матрицы ( X X ) 1
просто не существует. Оценку параметров
модели невозможно найти из нормального
векторного уравнения
X Xb X Y .
На практике строгая мультиколлинеарность встречается достаточно редко, т. к. её
несложно избежать на стадии предварительного отбора факторов модели.
5.
Чаще связь между объясняющимипеременными выражается в стохастической форме, когда они тесно коррелируют
друг с другом.
В этом случае говорят о нестрогой
мультиколлинеарности.
6.
Матрица X X хотя и неособенная, ноеё определитель X X близок к нулю.
Компоненты вектора оценок b обратно
пропорциональны величине определителя
и в силу этого имеют значительные
средние квадратические отклонения b , и,
следовательно, большие стандартные
ошибки mb j . Отсюда они нестабильны как
по величине, так и по знаку.
j
7.
В итоге отметим основные негативныепоследствия мультиколлинеарности:
большие дисперсии оценок D (b j )
параметров приводят к существенным
отклонениям оценок от оцениваемого
параметра, расширяет интервальные
оценки;
уменьшаются t статистики
параметров , что может привести к
неоправданному выводу о статистической
незначимости параметров b j и о несущественном влиянии соответствующего фактора
на результат y ;
8.
МНК- оценки b j коэффициентовмодели и их стандартные ошибки mb j
становятся очень чувствительными к
малейшему изменению исходных данных;
становится невозможным определить
изолированное влияние факторов на
результат y .
9.
Точных количественных критериев дляустановления или отсутствия мультиколлинеарности не существует. Но существуют
некоторые эвристические подходы к её
выявлению.
Один из них заключается в анализе
матрицы межфакторной корреляции
1
rx2 x1
Rx
rx x
p1
rx1 x2
rx1 x3
1
rx2 x3
rx p x2
rx p x3
rx1 x p
rx2 x p
1
10.
Считается, что если в ней содержатся коэффициенты корреляции, у которых rx x 0,75,то это свидетельствует о присутствии
нестрогой мультиколлинеарности.
Другой подход в оценке мультиколлинеарности состоит в исследовании
определителя матрицы X X . Если X X = 0 ,
то существует строгая мультиколлинеарность, а если он близок к нулю ( X X 0,1), то
это свидетельствует о наличии нестрогой
мультиколлинеарности.
i j
11.
Для оценки значимости мультиколлинеарности факторов можно использоватьопределитель матрицы межфакторной
корреляции R x . Если бы факторы не
коррелировали между собой, то все
внедиагональные элементы матрицы R x
равнялись бы нулю. Если же все rxi x j =1, то
определитель такой матрицы равнялся бы
нулю.
12.
Отсюда выдвигается гипотеза H 0 : Rx(отсутствие мультиколлинеарности).
Доказано, что статистика
1
n 1 1 / 6(2 p 5) lg Rx
2
имеет приближенное распределение «хиквадрат» с k 1 / 2n(n 1) степенями свободы.
Если ( , k ) , то гипотеза H 0 отклоняется
и мультиколлинеарность факторов считается
доказанной.
2
набл
2
кр
13.
Если мультиколлинеарность установлена,то каким образом её можно устранить?
Единого подхода к её устранению не
существует, но используются ряд методов,
которые применимы в конкретных
ситуациях.
14.
Самый простой из них заключается в том,что из двух объясняющих переменных,
имеющих высокий коэффициент корреляции
( rx x 0,75 ), одну из переменных исключают
из уравнения.
i j
Но здесь нужна осторожность, чтобы не
исключить переменную, которая необходима
в уравнении по своей экономической сущности, но зачастую коррелирует с другими
факторами.
15.
Другой метод заключается в увеличенииобъёма выборки, если это возможно:
большее количество данных позволяет
получить МНК-оценки с меньшей
дисперсией.
Например, при использовании ежегодных
данных можно перейти к поквартальным
данным и объем выборки увеличится в 4
раза.
16.
В следующем методе переходят отнесмещенных МНК-оценок параметров к
таким смещенным оценкам, которые
обладают меньшим рассеиванием
относительно математического ожидания
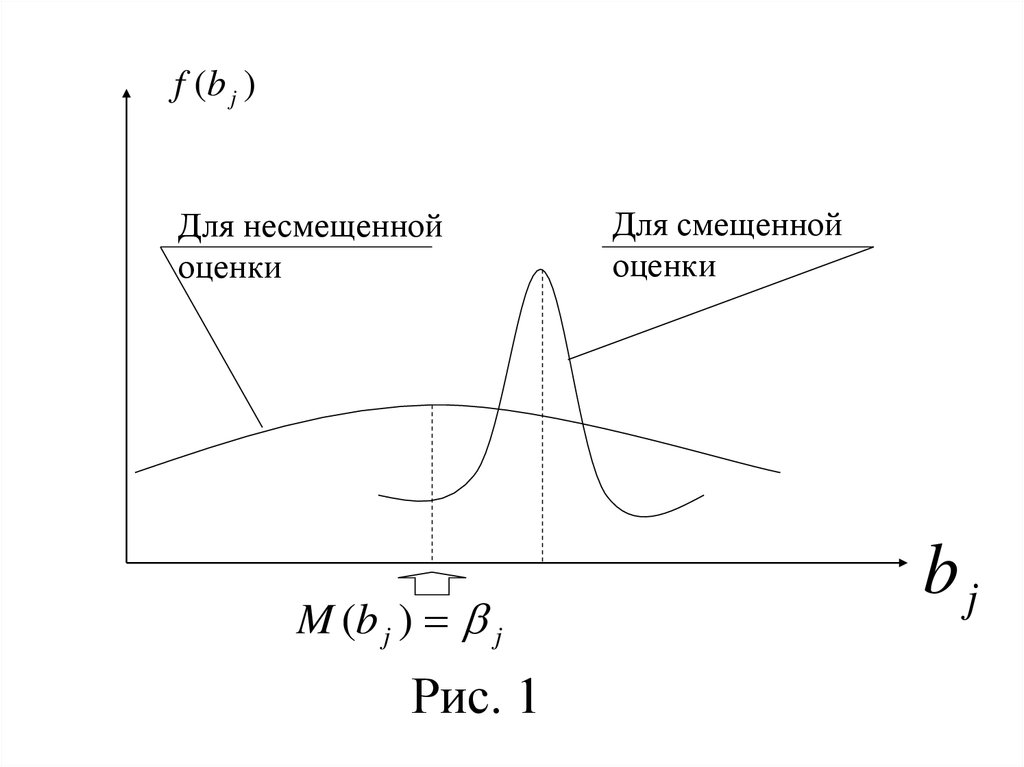
(рис. 1).
17.
f (b j )Для несмещенной
оценки
M (b j ) j
Рис. 1
Для смещенной
оценки
bj
18.
Например, при использовании «риджрегрессии» (гребневой регрессии)рассматривают смещенные оценки
b X X E p 1 X Y ,
1
где некоторое малое положительное
число называемое гребнем, E p 1
единичная матрица порядка p 1 .
Диагональные элементы матрицы X X при
этом увеличиваются на величину , а
остальные элементы остаются неизменными.
19.
Определитель матрицы X X E p 1увеличивается по сравнению с
X X
и эффект мультиколлинеарности
уменьшается.
При плохой обусловленности матрицы для
оценки параметров иногда применяют
метод главных компонент. Основная идея
метода состоит в замене исходных объясняющих переменных x j , j 1, p на новые
переменные zi , i 1, k. Новые переменные
(главные компоненты) должны обладать
следующими свойствами:
20.
полная совокупность главныхкомпонент должна содержать в себе всю
изменчивость исходных переменных
x j , j 1, p;
главные компоненты должны быть
ортогональны между собой, т. е. быть
линейно-независимыми.
21. 2. Гетероскедастичность
Предпосылка 3° МНК о постоянстведисперсий D( i ) случайных составляющих i
для всех наблюдений на практике не всегда
выполняется и имеет место гетероскедастичность модели.
Негативные последствия гетероскедастичности следующие:
22.
оценки коэффициентов модели,оставаясь несмещенными и состоятельными, уже не будут эффективными, и при
небольших объёмах выборок появляется
риск получения оценок b j , существенно
отличающихся от оцениваемого
коэффициента j ;
23.
стандартные ошибки параметров , какправило, будут заниженными, а t статистики
– завышенными, что приводит к признанию
статистической значимости параметров,
которые на самом деле таковыми не
являются;
дисперсии оценок D (b j ) будут
рассчитываться со смещением, что
существенно влияет на интервальные
оценки коэффициентов модели.
24.
Для обнаружения гетероскедастичностинаиболее простым является визуальный
метод.
Наличие гетероскедастичности для
парной регрессии можно наглядно видеть
из поля корреляции, когда дисперсия
случайных составляющих растет (или
уменьшается) по мере увеличения x
(рис. 2).
25.
yРис. 2
e
e
~
y b0 b1 x
x
2
~y
Рис. 3
e
2
~y
Рис. 4
~y
Рис. 5
26.
В некоторых случаях гетероскедастичностьвизуально не столь очевидна. Тогда применяют тесты на гетероскедастичность, причем
все они используют нулевую гипотезу об
отсутствии гетероскедастичности.
Тест ранговой корреляции Спирмена
использует наиболее общее предположение о
зависимости дисперсий ошибок от значений
объясняющей переменной x :
D( i ) fi ( xi ), i 1, n.
2
i
27.
Никаких дополнительных предположенийотносительно вида функций f i
и законе
распределения возмущений i здесь не
делается.
Идея теста заключается в том, что ei
является некоторой оценкой i , и поэтому в
случае гетероскедастичности значения eiи
будут
xi коррелировать.
28.
Рассмотрим применение теста на примере~
парной регрессии y b0 b1 x
. В тесте
используют коэффициент ранговой корреляции rxe , для нахождения которого
следует отдельно ранжировать наблюдения
по возрастанию переменной xi , когда каждое
значение xi получит свой ранг от 1 до n , а
таким же образом ранжировать остатки ei .
29.
В итоге коэффициент rxe вычисляется поn
формуле:
2
rxe 1
6 di
i 1
2
n(n 1)
,
(1)
где d i разность между рангами xi и ei .
Доказано, что при справедливости
гипотезы H 0 : rxe 0 статистика
T
rxe n 2
1 rxe2
имеет распределение Стьюдента с числом
степеней свободы k n 2 .
(2)
30.
Поэтому, если t набл превышает t кр ( 2 , k ) ,то гипотезу H 0 отклоняют и признают
наличие гетероскедастичности.
Для множественной регрессии
проверка гипотезы H 0 с помощью статистики (2) может выполняться по каждому
фактору отдельно.
31.
Тест Голдфельда-Квандта применяется втом случае, когда случайные величины i
имеют нормальное распределение и
cov( i , j ) 0, i j .
В нём предполагается, что дисперсии i2
возмущения i пропорциональны квадрату
переменной xi , т. е.
2
2 2
i xi .
На примере парной регрессии
~
y b0 b1 x
тест состоит из следующих этапов.
32.
1. Все наблюдений упорядочиваются впорядке возрастания переменной x .
2. Вся упорядоченная выборка разбивается
на три подвыборки объёмов соответственно l , n 2l , l (обычно l n / 3 ).
3. Оцениваются отдельно две регрессии
~y b b x, ~y b b x
10
11
20
21
для первой подвыборки (первые l наблюдений) и третьей подвыборки (последние
l наблюдений).
33.
Рассчитываются остаточные суммы дляобеих регрессий
l
s1 e , s2
i 1
2
i
4. Выдвигается гипотеза
n
e .
i n l 1
2
i
H 0 : ... ,
2
1
2
2
для проверки которой используется
статистика
2
n
34.
s2s , если s 2 s1 ,
F 1
s1
, если s1 s 2 ,
s 2
которая при справедливости гипотезы H 0
имеет распределение Фишера с k1 k2 l p 1
степенями свободы. Если Fнабл Fкр ( , k1 , k 2 ), то
гипотеза об отсутствии гетероскедастичности отклоняется на уровне значимости .
35.
Если в модели более одного фактора, товыборка упорядочивается по тому фактору,
который, как предполагается, теснее связан с
2
i .
При установлении гетероскедастичности
возникает необходимость преобразования
модели с целью устранения данного
недостатка.
36.
Если дисперсии известны, тогетероскедастичность легко устраняется.
Рассмотрим это на примере парной
регрессии
yi 0 1 xi i , i 1, n (3)
Разделим обе части уравнения (3) на
известное значение i i2
yi
xi
i
1
0
1
i
i
i
i
и сделаем замену переменных:
2
i
37.
yixi
i
1
y , xi , z i , i
i
i
i
i
i
Тогда получим модельное уравнение
x
регрессии с двумя факторами i , z i , но без
свободного члена
y 0 zi x i , i 1, n.
i
1 i
(4)
38.
Очевидно, что для любого наблюденияi
i2
1
D( i ) D( ) 2 D( i ) 2 1 const ,
i i
i
т.е. модель (4) является гомоскедастичной,
классической.
Полученные МНК - оценки b0 , b1
коэффициентов модели (4) будут наилучшими несмещенными оценками и их можно
использовать для первоначальной модели (3).
39.
Уравнение (4) представляет собой взвешенную регрессию с весами 1 / i .Наблюдения с наименьшими дисперсиями
получат наибольшие "веса" и наоборот.
Поэтому данную версию МНК называют
взвешенным методом наименьших
квадратов (ВМНК). В свою очередь он
является частным случаем обобщенного
метода наименьших квадратов (ОМНК),
когда оценки определяются по формуле:
ˆ
b X X
1
1
X Y .
1
40.
Здесь ковариационная положительноопределенная матрица ошибок, т.е. и
её диагональные элементы различны, а
внедиагональные элементы в общем случае
не равны нулю (в классической модели
представляет скалярную матрицу с одинако2
выми диагональными элементами ).
41.
На практике значения i2 неизвестны.Поэтому, чтобы применить ВМНК,
необходимо сделать реалистические
2
предположения о значениях i . В этих
случаях говорят не об устранении, а о
смягчении гетероскедастичности.
2
Если предположить, что дисперсии i
пропорциональны значениям xi
xi , i 1, n,
2
i
2
42.
тогда уравнение (3) преобразуется вгомоскедастичную модель делением обеих
его частей на xi :
y 0 zi x i ,
i
1 i
где
yi
xi
i
1
y
, xi
, zi
, i
.
xi
xi
xi
xi
i
43.
Если же предположить, что дисперсиипропорциональны значениям квадратов xi
2
i
x , i 1, n,
2
i
2 2
i
то делением обеих его частей на величину xi
можно получить гомоскедастичную модель
y 0 zi 1 i .
i
Отметим, что параметры в последней
модели по сравнению с уравнением (3)
поменялись ролями: 0 коэффициент
регрессии, 1 свободный член.










































 Математика
Математика








