Непрерывно-детерминированные модели (D-схемы)

1. 3. Непрерывно-детерминированные модели (D-схемы)

На примере
дифференциальных
уравнений

2. Основные соотношения

Математическое соотношение (6) для
детерминированных систем может определяться
условиями
y t f y t , t ,
(7)
y t0 y0 ,
где
dy
y t y1 , y2 , , yn , y
,
dt
f f1 , f 2 , , f n вектор-функция,
Уравнения 1-го
порядка
непрерывная на некотором (n+1)-мерном
множестве,

3.

или
y t f y t , y t , t ,
y t0 y0 , y t0 y0 ,
и т. д.
(7')
Уравнения 2-го
порядка

4.

В простейшем случае (одна выходная характеристика)
дифференциальные уравнения принимают вид
y t f y t , t ,
y t f y t , y t , t ,
и т. д.

5.

Общее уравнение D-схемы (для одного входа и одного
выхода) имеет вид
m m 1
n n 1
F y , y , , y , x , x , , x 0 ,
где
х, у – функции от t,
n
d n y m d m x
y n , x m .
dt
dt
(8)

6.

Схемы вида (7) – (8) отражают динамику изучаемой
системы (поведение во времени)
называются D-схемами (англ. dynamic).

7. Примеры

1. Элементарная система механической природы.
Процесс свободных колебаний маятника
описывается обыкновенным дифференциальным
уравнением
ml 2
d 2 t
dt
2
mgl t 0 ,
m, l – масса, длина подвеса маятника,
g
– ускорение свободного падения,
θ(t) – угол отклонения маятника в
момент времени t.
l
θ
m

8.

Из уравнения можно получить оценки характеристик
системы.
Например, период колебаний маятника
l
T 2
.
g

9.

2. Элементарная система электрической природы.
Процессы в электрическом колебательном контуре
описываются обыкновенным дифференциальным
уравнением
L
d 2q t
dt 2
1
q t 0 ,
C
L – индуктивность,
C – емкость конденсатора,
q(t) – заряд конденсатора в
момент времени t.
L
q
C

10.

Из уравнения можно получить оценки характеристик
системы.
Например, период характеристических колебаний
T 2 LC .

11.

Введем обозначения:
1
h0 ml 2 h0 L , h1 0, h2 mgl h2 ,
C
z t t z t q t .
Получим диф. уравнение 2-го порядка, описывающее
поведение замкнутой системы:
h0
d 2 z t
dt
2
dz t
h1
h2 z t 0 ,
dt
(9)
где h0, h1, h2 – параметры системы;
z(t) – состояние системы в момент времени t
(и выходная характеристика).

12.

Выводы:
поведение двух рассмотренных выше систем
разной природы может быть исследовано на
основе общей математической модели (9);
поведение одной из систем может быть
проанализировано с помощью другой.

13.

Если изучаемая система S (маятник или контур)
взаимодействует с внешней средой Е,
то появляется входное воздействие x(t) (внешняя
сила для маятника или источник энергии для
контура).
Непрерывно-детерминированная модель такой
системы примет вид
h0
d 2 z t
dt 2
dz t
h1
h2 z t x t .
dt
Выходная
характеристика
(y=z)
Входное
(управляющее)
воздействие

14. Возможные приложения (САУ)

Система управления (СУ) – это совокупность
взаимодействующих между собой объекта управления
(управляемой системы) и управляющего устройства,
деятельность которых направлена на достижение
заданной цели управления.
Целью управления является изменение какого-либо
параметра (параметров), характеризующего состояние
объекта управления, в соответствии с определенным
законом.
Этот параметр (совокупность параметров) –
управляемая (выходная) переменная.

15. Структурная схема системы управления

v
х
УУ
Обратная
связь
u
ИМ
u'
y
ОУ
Датчики
v1
УУ – управляющее устройство; ОУ – объект управления;
ИМ – исполняющий механизм (усиливает и/или
преобразует сигнал управления и воздействует на ОУ);
х – задающее воздействие (внешнее воздействие, которое
определяет закон изменения выходной переменной);
v – возмущающее воздействие (среда);
v1 – шумы измерений.

16. Основные задачи систем управления

1. Стабилизация системы – поддержание заданного
режима работы, несмотря на действие помех.
x = const.
Примеры:
• стабилизация напряжения и частоты тока в сети вне
зависимости от изменения потребления энергии;
• авторулевые на судах (поддержание заданного курса).

17.

2. Выполнение программы – управление по заранее
заданной программе (задающее воздействие меняется,
но закон изменения известен).
x = x(t).
Примеры:
• полет ракеты;
• системы бытовой техники (стиральные машины и др.).

18.

3. Слежение за неизвестным задающим сигналом.
Задающее воздействие заранее неизвестно и
определяется внешними факторами.
Примеры:
• слежение за самолетом в радиолокационной станции
слежения;
• управление производством в условиях изменения
спроса.

19.

В САУ управление объектом осуществляется без
непосредственного участия человека
автоматическими устройствами на основе
запрограммированных алгоритмов управления.
Участие человека имеет место при разработке
алгоритмов и программ.
Основные функции САУ:
• автоматический контроль и измерения,
• автоматическая сигнализация,
• автоматическая защита,
• автоматические пуск и остановка различных
двигателей и приводов,
• автоматическое поддержание заданных режимов
работы оборудования,
• автоматическое регулирование.

20. Оператор системы

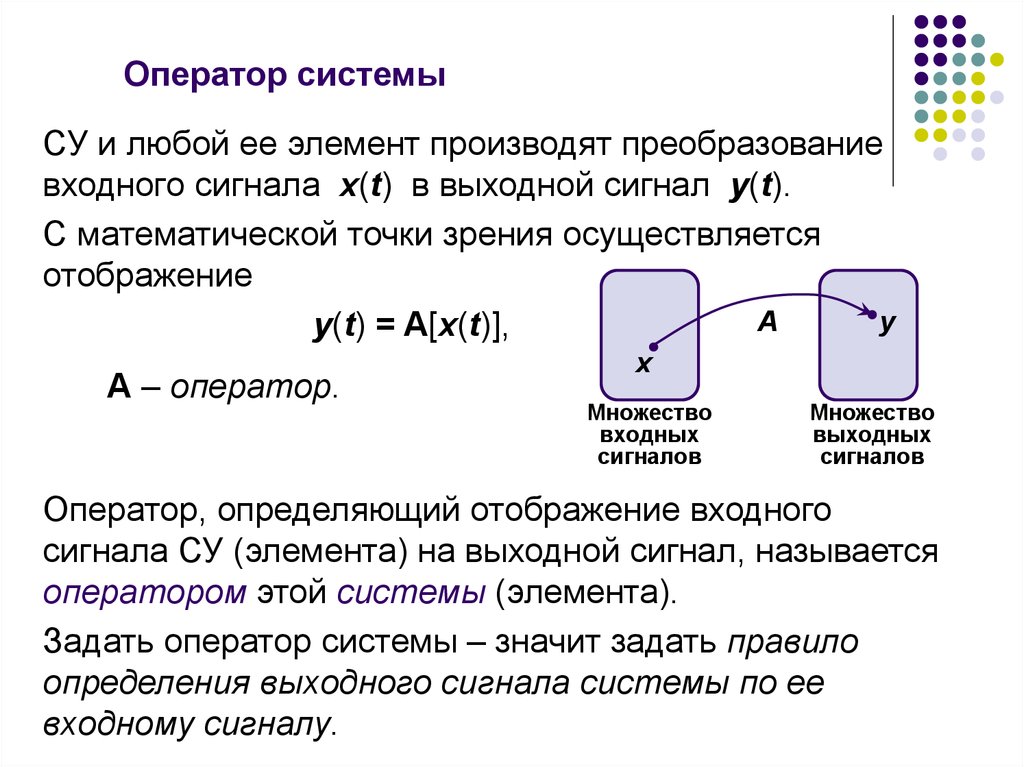
СУ и любой ее элемент производят преобразование
входного сигнала x(t) в выходной сигнал y(t).
С математической точки зрения осуществляется
отображение
A
y
y(t) = A[x(t)],
A – оператор.
x
Множество
входных
сигналов
Множество
выходных
сигналов
Оператор, определяющий отображение входного
сигнала СУ (элемента) на выходной сигнал, называется
оператором этой системы (элемента).
Задать оператор системы – значит задать правило
определения выходного сигнала системы по ее
входному сигналу.

21.

Примеры.
t
1. Оператор интегрирования
A x t x t dt .
0
Описывает, например, наполнение пустого бака водой.
Если сечение бака S (м2) постоянно по всей высоте, то
где
1t
h t q t dt ,
S0
h(t) – уровень воды, q(t) – поток воды (м3/с).

22.

2. Оператор дифференцирования
dx t
A x t x t
.
dt
Применяется в электротехнике:
du t
i t C
.
dt
i – ток (в амперах),
и – разность потенциалов (в вольтах) на пластинах
конденсатора,
С – емкость конденсатора (в фарадах).
di t
u t L
.
dt
и – падение напряжения на катушке индуктивности,
L – индуктивность (в генри).

23. Звенья

Звено – это математическая модель системы или
любой ее подсистемы, определяемой некоторым
оператором.
В частности, звено может быть математической
моделью элемента.
Математическая модель СУ может быть представлена
в виде соединения звеньев.

24. Линеаризация СУ

По виду операторов, которыми описывается СУ,
системы подразделяют на
линейные (все звенья описываются линейными
операторами);
нелинейные (некоторые звенья описываются
нелинейными операторами).
Большинство реальных СУ первоначально
описываются нелинейными моделями.
Путем линеаризации (преобразования исходных
нелинейных уравнений в линейные) может быть
получена линейная модель.

25.

После линеаризации непрерывная СУ с одним входом х
и одним выходом у может быть описана уравнением
( n)
( n 1)
a0 y a1 y an y
(m)
( m 1)
b0 x b1 x bm x .
(10)

26.

Введем обозначение для операции
дифференцирования:
d
p ,
dt
Равенство по
определению
p2
d2
dt
, ,
2
pi
di
dt
i
,
p – оператор
дифференцирования

27.

Тогда уравнение (10) может быть записано в
операторной форме:
( n)
( n 1)
a0 y a1 y an y
(m)
(10)
( m 1)
b0 x b1 x bm x
a0 pn y a1 pn 1 y an y
b0 pm x b1 pm 1 x bm x
a p
0
n
a1 pn 1 an y b0 pm b1 pm 1 bm x . (11)

28.

Обозначим
Q p a0 p n a1 p n 1 an ,
Собственный
оператор СУ
P p b0 p m b1 p m 1 bm .
Оператор
воздействия
Тогда уравнение СУ запишется в виде:
Q p y P p x .
(11')
Уравнения (10), (11), (11') описывают модель «входвыход» (связывают входные и выходные переменные
системы).

29. Передаточные функции

Передаточной функцией называется отношение
оператора воздействия к собственному оператору.
P p
W p
Q p
Это оператор.
Его нельзя рассматривать,
как обычную дробь.
Степень многочлена Q(p) называется порядком
передаточной функции и соответствующей системы
(звена).

30.

Запись уравнения СУ (звена) с помощью передаточной
функции:
b0 pm b1 pm 1 bm
y W p x
x.
n
n 1
a0 p a1 p an
(12)
Передаточные функции полностью описывают связи
между выходом и входами объекта, но не учитывают
внутреннее устройство объекта.

31.

Пример.
Пусть звено СУ описывается дифференциальным
уравнением
0,1 y 1,2 y y 2 x x .
Уравнение в операторной форме:
0,1 p
2
1,2 p 1 y 2 p 1 x .
Собственный оператор
Оператор воздействия
2 p 1
;
Передаточная функция равна W p
2
0,1 p 1,2 p 1
уравнение звена с помощью передаточной функции:
2p 2
y W p x
x.
2
0,1 p 1,2 p 1

32. Принцип суперпозиции

Для линейных СУ:
реакция системы на несколько одновременно
действующих воздействий равна сумме реакций на
каждое воздействие в отдельности.
Для системы с двумя входами u(t) и v(t)
обозначим yu(t) – реакция системы при u=u(t), v = 0;
yv(t) – реакция системы при v=v(t), u = 0.
Тогда реакция системы при u=u(t), v=v(t):
y(t) = yu(t) + yv(t).
Принцип суперпозиции позволяет во многих случаях
ограничиться изучением систем с одним входом.

33. Переходная функция

Один из методов построения и исследования моделей
«вход-выход» – определение реакции СУ (звена) на
некоторый стандартный тестовый сигнал.
Простейший сигнал – «единичный скачок»
(«единичный ступенчатый сигнал»).
Описывается функцией 1(t):
1 при t 0,
1(t) =
0 при t 0.
1(t)
1
O
t

34.

Переходной функцией СУ (звена) называется
функция, описывающая реакцию системы на
единичное ступенчатое воздействие при нулевых
начальных условиях.
Обозначение – h(t).
График переходной функции (зависимость h(t) от t)
называется переходной характеристикой.
Z

35.

Пример.
Пусть звено описывается диф. уравнением 1-го
порядка
Ty y k x.
Решение уравнения при х(t) = 1(t) и нулевых
начальных условиях ( y(0) = 0 ):
t
h t y t k 1 e T
.
Т – постоянная времени звена
(характеризует инерционность
звена: чем больше Т, тем
медленнее реакция объекта на
управление).

36. Структурные схемы

Структурной схемой СУ называется графическое
представление ее математической модели в виде
соединений звеньев, представляемых
прямоугольниками или кругами (сумматоры), с
указанием входных и выходных переменных.
Обычно внутри прямоугольника – условное
обозначение оператора звена, а сам оператор
(диф. уравнение или передаточная функция)
задается вне структурной схемы.

37.

Изображение сумматоров.
суммирование:
g+x
g
x
вычитание:
g–x
g
–
x
Если перед входом стоит «–»,
то переменная по этому
входу вычитается

38. Последовательное соединение звеньев

Так называется соединение, при котором выходная
переменная предшествующего звена является входной
переменной последующего звена.
При последовательном соединении передаточные
функции звеньев перемножаются.
Преобразование схемы: цепочку из последовательно
соединенных звеньев с передаточными функциями
W1(р), W2(р), … , Wn(р) можно заменить одним звеном
c передаточной функцией W(р) = W1(р)W2(р)…Wn(р).
х0
W1
х1
W2
…
Wn
хn
х0
W
хn

39. Параллельное соединение звеньев

Так называется соединение, при котором на входы
всех звеньев подается одно и то же воздействие, а их
выходные переменные складываются.
При параллельном соединении передаточные функции
звеньев складываются.
Преобразование схемы: параллельно соединенные звенья
с передаточными функциями W1(р), W2(р), … , Wn(р)
можно заменить одним звеном c передаточной функцией
W(р) = W1(р)+W2(р)+…+Wn(р).
y
W1
x
…
W2
Wn
1
y2
yn
n
y yi
i 1
x
W
y

40. Обратное соединение (звено, охваченное обратной связью)

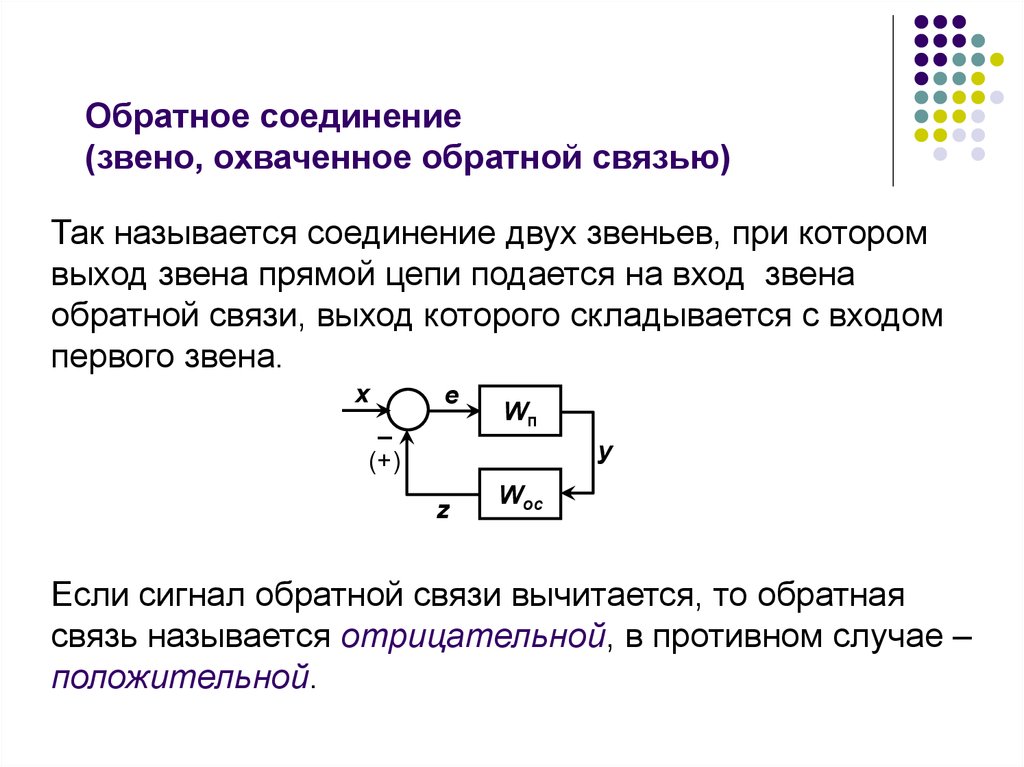
Так называется соединение двух звеньев, при котором
выход звена прямой цепи подается на вход звена
обратной связи, выход которого складывается с входом
первого звена.
x
e
–
(+)
Wп
y
z
Wос
Если сигнал обратной связи вычитается, то обратная
связь называется отрицательной, в противном случае –
положительной.

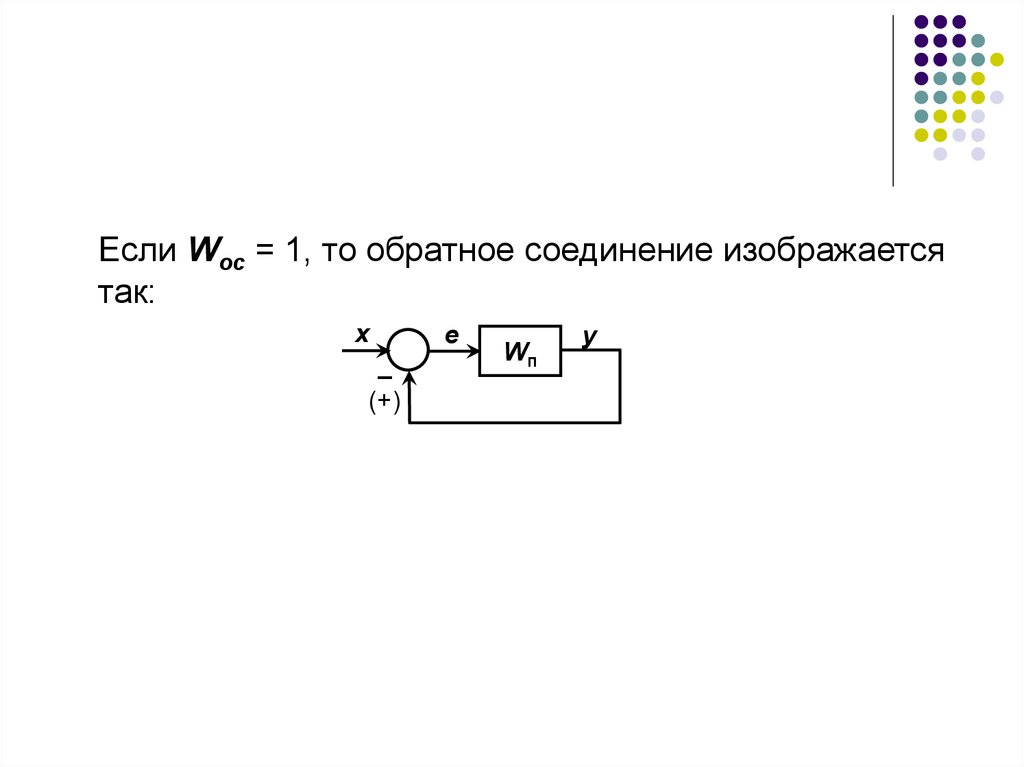
41.

Если Wос = 1, то обратное соединение изображается
так:
x
–
(+)
e
Wп
y

42.

Передаточная функция при обратном соединении
равна
Wп p
W p
,
1 Wк p
где
Wк(р) = Wп(р)Wос(р)WΣ(р),
Передаточная функция контура
1 при отрицательной обратной связи,
W p
1 при положительной обратной связи.
Передаточная функция сумматора
по входу обратной связи

43.

Пример.
x
e
–
W1
z
W2
W3
y
W4
Передаточная функция прямой цепи относительно
входа x и выхода y: Wп = W1W2W3
(вход сумматора имеет знак «+»).
Передаточная функция обратного соединения
(относительно входа x и выхода у) равна
Wп
W1W2W3
W yx
1 Wк
1 W1W2W3W4
(обратная связь отрицательна).

44. Анализ непрерывных САУ

Включает
исследование системы на устойчивость;
исследование качества управления в переходном
и установившемся режиме.
Исходные данные – математические модели СУ.

45.

Устойчивость – одно из основных требований к САУ.
Требуется:
путем выбора структуры и параметров СУ
обеспечивать ее устойчивость.

46. Определение устойчивости

Если на СУ действуют два внешних воздействия:
задающее воздействие x и возмущение v, то в общем
случае она описывается уравнением
( n)
( n 1)
(m)
( m 1)
a0 y a1 y an y b0 x b1 x bm x
(l )
( l 1)
c0 v c1 v cl v ,
(13)

47.

или, в операторной форме:
a p
0
n
a1 p n 1 an y b0 p m b1 p m 1 bm x
x t
(13′)
c0 p l c1 p l 1 cl v .
v t
При x ≡ 0 и v ≡ 0 – однородное дифференциальное
уравнение:
(14)
a0 pn a1 pn 1 an y 0.

48.

Назначение СУ – поддержание заданного режима,
называемого невозмущенным движением.
Если на систему действует возмущение, то
фактическое движение – возмущенное движение –
отличается от невозмущенного.

49.

Невозмущенное движение называется
асимптотически устойчивым, если после окончания
действия возмущения возмущенное движение y(t)
стремится к невозмущенному движению yн(t):
y(t) → yн(t)
при
t .
Линейная СУ называется асимптотически
устойчивой, если любое ее невозмущенное движение,
определяемое задающим воздействием,
асимптотически устойчиво.

50.

Общее решение уравнения (13′) имеет вид
y(t) = yв(t) + yс(t),
Описывает свободное движение
СУ (при отсутствии внешних
воздействий), определяемое
только начальными условиями
где yс(t) – общее решение
однородного уравнения (14),
yв(t) – частное решение Описывает вынужденное
движение СУ, определяемое
уравнения (13′).
внешними воздействиями
Частное решение yв(t) по принципу суперпозиции
yв(t) = yx(t) + yv(t),
где yx(t) – частное решение уравнения (13′) при v 0 ,
yv(t) – частное решение уравнения (13′) при x 0 .

51.

При отсутствии возмущающих воздействий (v ≡ 0)
yв(t) = yx(t) = yн(t).
Если в начальный момент времени t0 возмущение
Такое возмущение
перестает действовать, то
y(t) = yн(t) + yс(t)
при t ≥ t0 .
влияет на начальные
условия, от которых
зависит только
свободное движение
Для того, чтобы невозмущенное движение было
асимптотически устойчиво ( y(t) → yн(t) при t ),
необходимо и достаточно, чтобы
lim yc t 0 .
t
Математическое определение
асимптотической устойчивости
линейных непрерывных
стационарных СУ

52. Характеристическое уравнение СУ

Характеристическое уравнение СУ, которая
описывается уравнением (13), – это характеристическое
уравнение дифференциального уравнения (14):
Q a0 n a1 n 1 an 0 .
(15)
Q(λ) – характеристический полином;
он получается из собственного оператора системы
Q p a0 pn a1 pn 1 an
подстановкой р = λ:
Q Q p
p
.

53. Основное условие устойчивости

Если λi, i = 1, 2, …, q – корни уравнения (15)
кратности ki (k1 + k2 + … + kq = n), то можно
показать, что
yc t 0
при t
Re i 0
для всех i = 1, 2, …, q.
Отсюда – основное условие устойчивости:
для того, чтобы СУ была устойчива, необходимо и
достаточно, чтобы все корни ее
характеристического уравнения имели
отрицательную действительную часть.

54. Необходимое условие устойчивости

Для того, чтобы СУ была устойчива, необходимо,
чтобы все коэффициенты ее характеристического
уравнения (15) были строго одного знака:
или
a0 0, a1 0, , an 0
(16)
a0 0, a1 0, , an 0 .
(16′)
При невыполнении условий (16) и (16′) система
неустойчива;
при выполнении (16) или (16′) система может быть
устойчивой.

55. Алгебраические критерии устойчивости

Это проверка условий, накладываемых на
коэффициенты характеристического уравнения
(полинома).
В результате: корни характеристического
уравнения можно не вычислять.

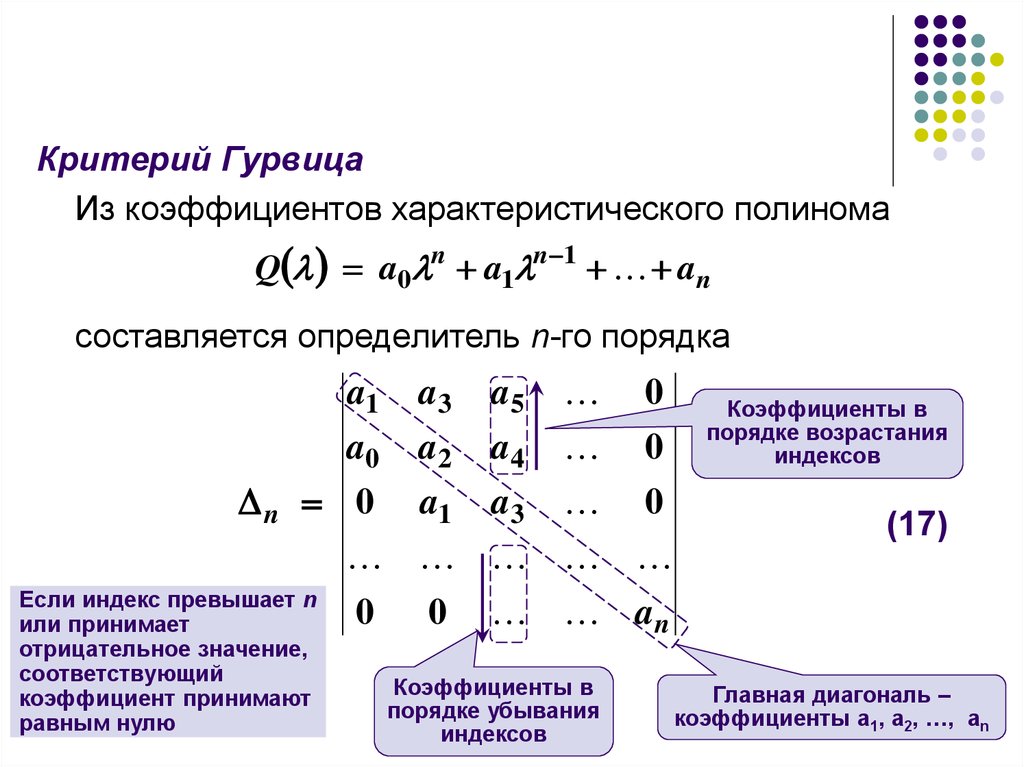
56.

Критерий Гурвица
Из коэффициентов характеристического полинома
Q a0 n a1 n 1 an
составляется определитель n-го порядка
a1 a3
a0 a 2
n 0 a1
Если индекс превышает n
0 0
или принимает
отрицательное значение,
соответствующий
коэффициент принимают
равным нулю
a5
a4
a3
0
0
0
an
Коэффициенты в
порядке убывания
индексов
Коэффициенты в
порядке возрастания
индексов
(17)
Главная диагональ –
коэффициенты а1, а2, …, аn

57.

Главные миноры определителя (17)
1 a1 , 2
a1
a3
a0
a2
a1
a3
a5
, 3 a0
a2
a4 , ,
0
a1
a3
включая сам определитель Δn, называются
определителями Гурвица.

58.

Критерий Гурвица (Hurwitz, 1895):
для того, чтобы СУ была устойчива, необходимо и
достаточно, чтобы определители Гурвица,
составленные из коэффициентов ее
характеристического уравнения при а0 > 0 были
больше нуля:
а0 > 0, Δ1 > 0, Δ2 > 0, …, Δn > 0.

59.

Критерий Льенарда-Шипарда
При выполнении необходимого условия
устойчивости для проверки устойчивости СУ
необязательно вычислять все определители Гурвица.
Критерий Льенарда-Шипарда (Lienard, Chipard, 1914):
при выполнении необходимого условия устойчивости
(16) для устойчивости СУ необходимо и достаточно,
чтобы выполнялось условие
Определители Гурвица
с четными индексами
Δ2 > 0, Δ4 > 0, Δ6 > 0, …
(18)
или
Δ3 >
Следствие:
при n = 1 и n = 2
необходимое условие
устойчивости является
и достаточным
0, Δ5 > 0, Δ7 > 0, …
Определители Гурвица с
нечетными индексами
(18′)

60.

Пример.
Исследуем устойчивость разомкнутой и замкнутой
систем
x
W(р)
x
y
e
W(р)
y
–
где
k
W p
, k 0,5; 2 .
2
p p 1 p
Характеристический полином разомкнутой системы
Q(λ) = λ3 + λ2 + λ;
а0 = а1 = а2 = 1, а3 = 0.
Необходимое условие устойчивости не выполняется,
разомкнутая система неустойчива при любом k.

61.

Передаточная функция замкнутой системы равна
Wп p
W p
k
Wз p
,
2
1 Wк p
1 W p
p p 1 p k
характеристический полином замкнутой системы
Q*(λ) = λ3 + λ2 + λ + k; а0 = а1 = а2 = 1, а3 = k.
Все коэффициенты строго положительны при обоих
значениях k поэтому
• система может быть устойчивой;
• в качестве достаточного условия можно
использовать (18) или (18').

62.

В данном случае проще проверять условие (18).
При k = 0,5
a1 a3
1 0,5
2
1 0,5 0,5 0 ,
a0 a 2
1 1
замкнутая система устойчива.
При k = 2
2
a1
a0
a3
1 2
1 2 1 0,
a2
1 1
замкнутая система неустойчива.

63. Определение области устойчивости

При заданной структуре (состав элементов и связи
между ними) СУ какие-либо параметры могут не быть
фиксированными (их можно изменять). Такие
параметры называются варьируемыми.
Областью устойчивости в пространстве параметров
называется множество всех значений варьируемых
параметров, при которых система устойчива.

64.

Если существуют такие значения варьируемых
параметров, при которых система устойчива
(существует область устойчивости), то система
называется структурно устойчивой.
В противном случае система называется структурно
неустойчивой.
В простейших случаях область устойчивости можно
определить с помощью алгебраических критериев
устойчивости.

65.

Пример.
Определим область устойчивости замкнутой
системы на плоскости параметров (k, T).
x
e
W(р)
y
–
W p
k
Tp 1
3
.
Характеристический полином замкнутой системы
имеет вид
Q T 3 3 3T 2 2 3T 1 k .
Необходимое условие устойчивости:
Т 3 > 0, 3T 2 > 0, 3T > 0, 1+k > 0,
откуда T > 0, k > –1.

66.

Применим критерий Льенарда-Шипарда:
2
a1
a3
a0
a2
3T 2 1 k
3
3
3
8 k 0 .
9
T
T
1
k
T
3
T
3T
С учетом необходимого условия:
T 0,
1 k 8 .
Эта система неравенств определяет область
устойчивости.
T
–1
O
8
k

67. Показатели качества СУ

Под качеством системы управления понимается
совокупность показателей, которые прямо или
косвенно характеризуют точность ее работы.
О качестве СУ имеет смысл говорить, если она
устойчива
показатели качества определяют в
предположении устойчивости системы.

68.

Наиболее полная характеристика качества СУ – ошибка
е(t) = x(t) – y(t).
Это функция времени, что не очень удобно.
На практике при оценке качества СУ используют
числовые показатели, которые характеризуют
точность воспроизведения заданного движения.

69.

Показатели качества:
• в переходном режиме;
• в установившемся режиме.
Показатели качества как характеристики свойств
системы находят при определенных внешних
воздействиях, называемых типовыми.

70. Прямые показатели качества в переходном режиме

Типовое воздействие – ступенчатое воздействие А∙1(t).
Обычно принимают А = 1 (характер переходного
процесса не зависит от величины А: y(t) = A∙h(t) ).
Реакция
системы на
воздействие 1(t)
Ошибка
e(t) = 1(t) – h(t)
отличается от переходной функции на постоянную
величину.

71.

Прямые показатели качества – это показатели,
которые получаются непосредственно по переходной
характеристике.
Наиболее часто используются:
• время регулирования;
• перерегулирование.

72.

Время регулирования.
Временем регулирования tp называется
минимальное время (с момента подачи ступенчатого
воздействия), по истечении которого отклонение
выходной величины от установившегося значения
h(∞) не превышает некоторой заданной величины Δ.
t p min T p : h t h , t T p
Tp
Обычно принимают Δ = (0,05÷0,1)∙h(∞).

73.

Определение времени регулирования по
переходной характеристике:
у
hm
у = h(t)
tp – значение t, при
котором кривая y = h(t)
в последний раз
пересекает любую из
прямых y = h(∞)+Δ
или y = h(∞)–Δ.
h(∞)+Δ
h(∞)
h(∞)–Δ
О
tp
t

74.

Перерегулирование.
Перерегулирование σ определяется следующим
образом:
hm h
100% ,
h
где hm – максимальное значение переходной
функции.
Это максимальное отклонение переходной функции
от установившегося значения h(∞), выраженное в
процентах по отношению к h(∞).

75.

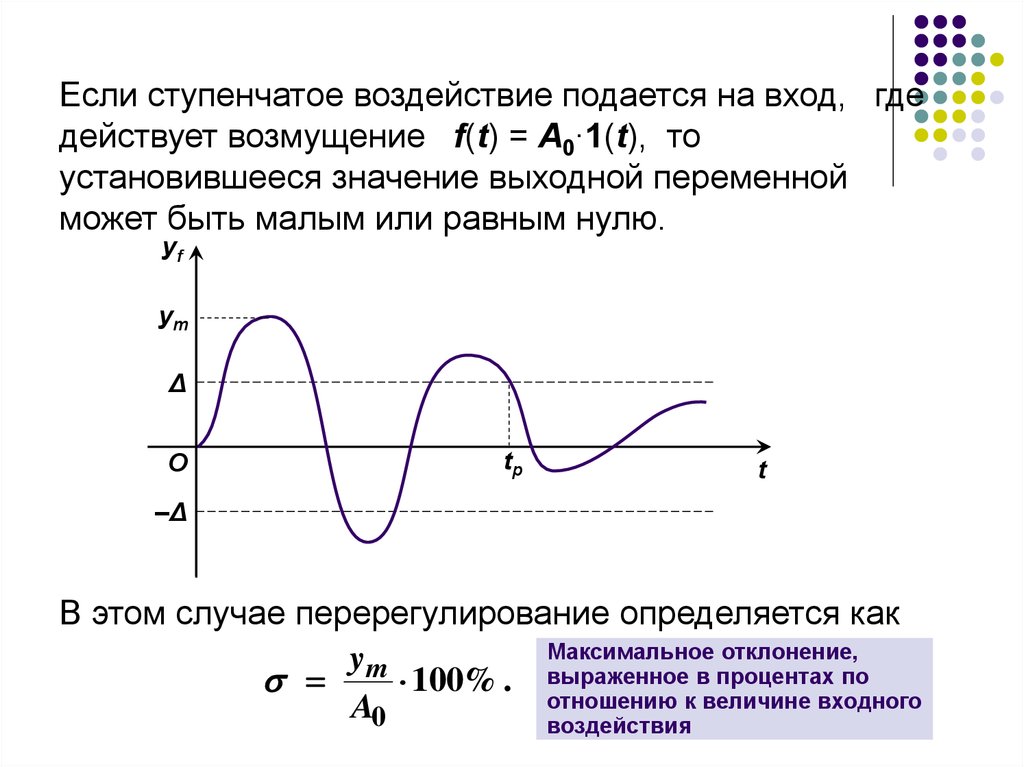
Если ступенчатое воздействие подается на вход, где
действует возмущение f(t) = A0∙1(t), то
установившееся значение выходной переменной
может быть малым или равным нулю.
уf
ym
Δ
О
tp
t
–Δ
В этом случае перерегулирование определяется как
Максимальное отклонение,
ym
100% . выраженное в процентах по
отношению к величине входного
A0
воздействия

76.

Другие прямые показатели
• Число колебаний за время регулирования tp.
Обозначение – Nk.
Можно рассматривать как прямой численный
показатель интуитивного понятия «колебательность»
системы.
• Время нарастания tн – время первого достижения
установившегося значения.

77. Общая модель САУ

В общем случае САУ описывается следующими
величинами.
Эндогенные переменные:
x t – вектор входных (задающих) воздействий;
v t – вектор возмущающих воздействий;
1
h t – вектор сигналов ошибки;
2
h t – вектор управляющих воздействий.
Экзогенные переменные:
z t – вектор состояний системы S;
y t – вектор выходных переменных.
t .
y
t
z
Обычно

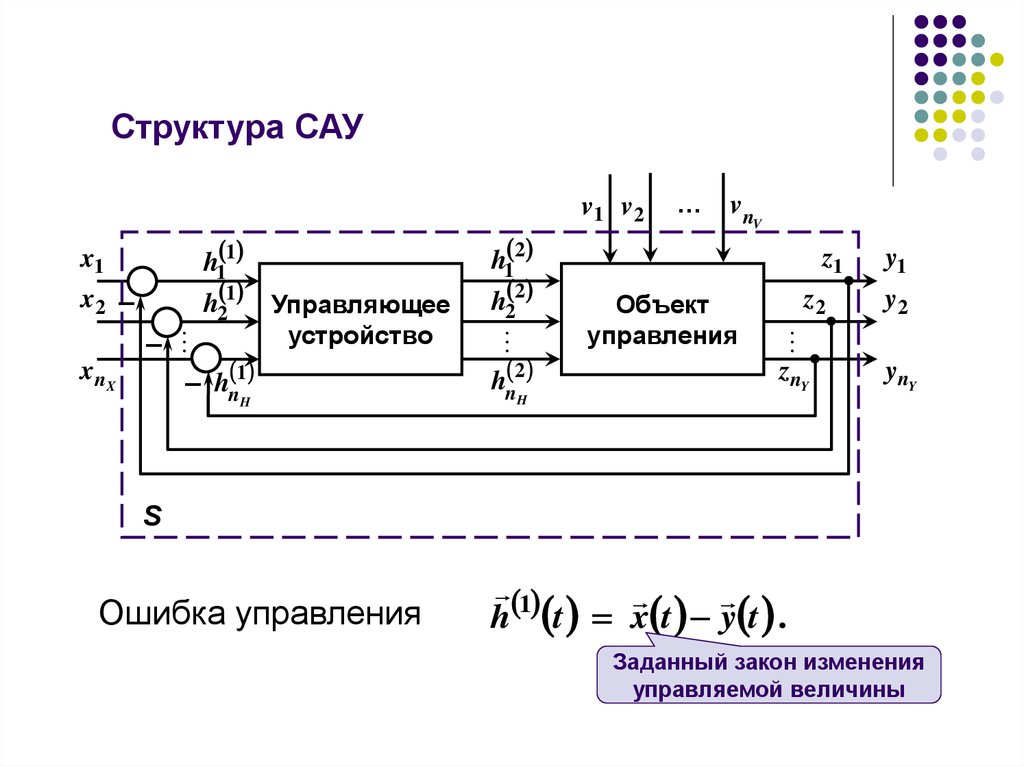
78. Структура САУ

v1 v 2
h1 1
h2 1
x1
x2 –
xn X
–
– hn 1
Управляющее
устройство
H
h1 2
h2 2
hn 2
…
vn
V
z1
Объект
управления
z2
z nY
y1
y2
ynY
H
S
Ошибка управления
1
h t x t y t .
Заданный закон изменения
управляемой величины

79.

При проектировании и эксплуатации САУ –
выбор параметров системы S, которые обеспечили бы
требуемую точность управления,
устойчивость системы в переходном процессе.
Для устойчивой системы практический интерес
представляют
• поведение системы во времени,
• максимальное отклонение регулируемой переменной
y(t) в переходном процессе,
• время переходного процесса и т. п.

80.

Итог:
использование D-схем позволяет
формализовать процесс функционирования
непрерывно-детерминированных систем;
оценить основные характеристики этих систем,
применяя аналитический подход и/или
имитационный подход.