Похожие презентации:
Модели на основе передаточных функций
1. МОДЕЛИ НА ОСНОВЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
2. Математическое моделирование электромеханической системы с использованием передаточных функций
Математическое моделирование электромеханической системы с использованием
передаточных функций
Передаточными
функции
при
исследовании
систем,
объектов,
элементов пользуются при
их
структурном моделирование.
Изображение
системы
(объекта)
представляют в этом случае в виде
совокупности динамических звеньев с
указанием связей между ними.
3.
Такое представление систем называетсяструктурной схемой.
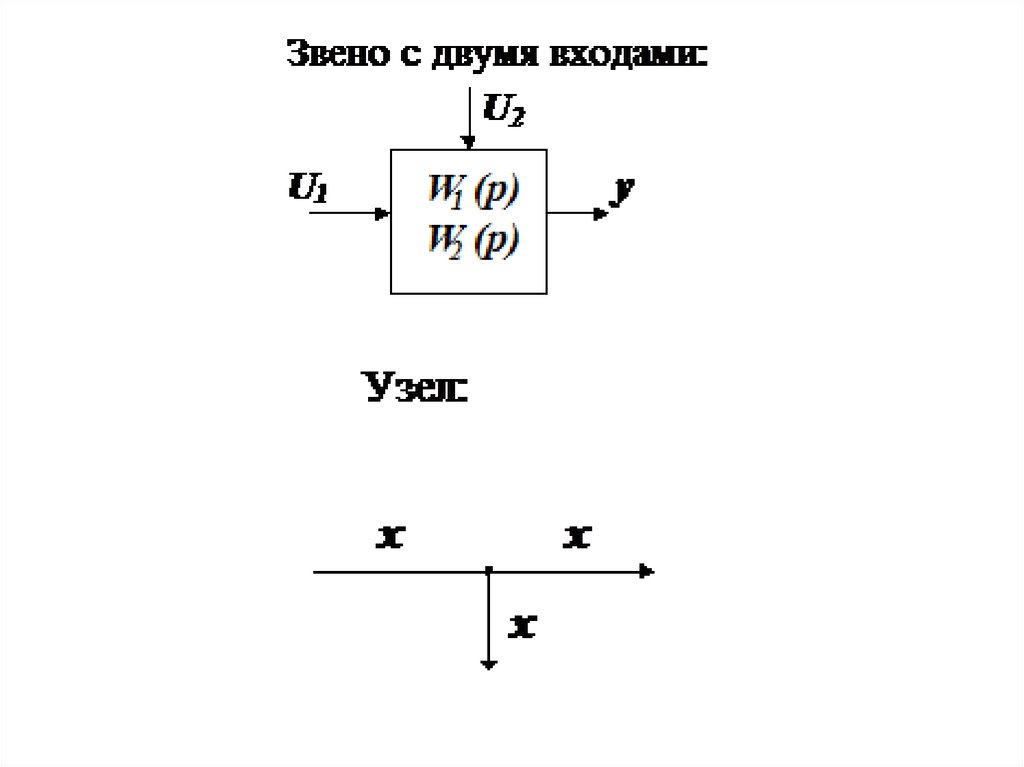
Графическое
изображение
основных
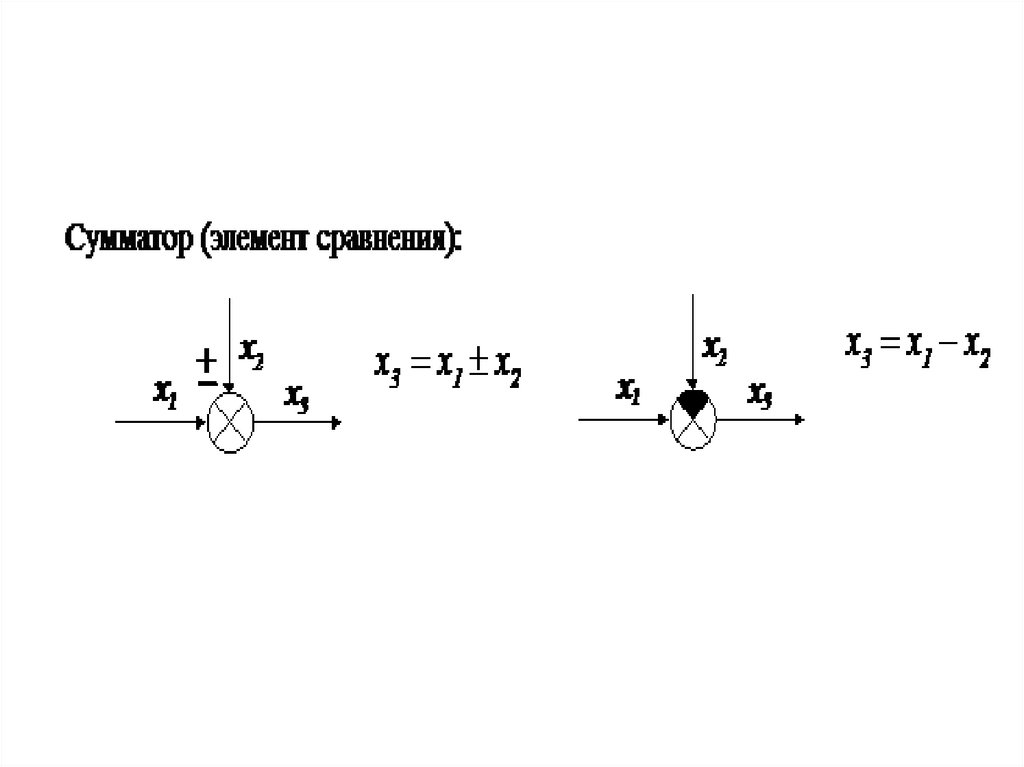
звеньев системы имеют следующий вид:
4.
5.
6. Математическая модель электромеханической системы постоянного тока
Рассмотрим структурную математическуюмодель электромеханической следящей
системы постоянного тока.
Основой для разработки структурной модели
являются прежде всего математическое
описание системы, которое формируется в
соответствии с ее функциональной схемой.
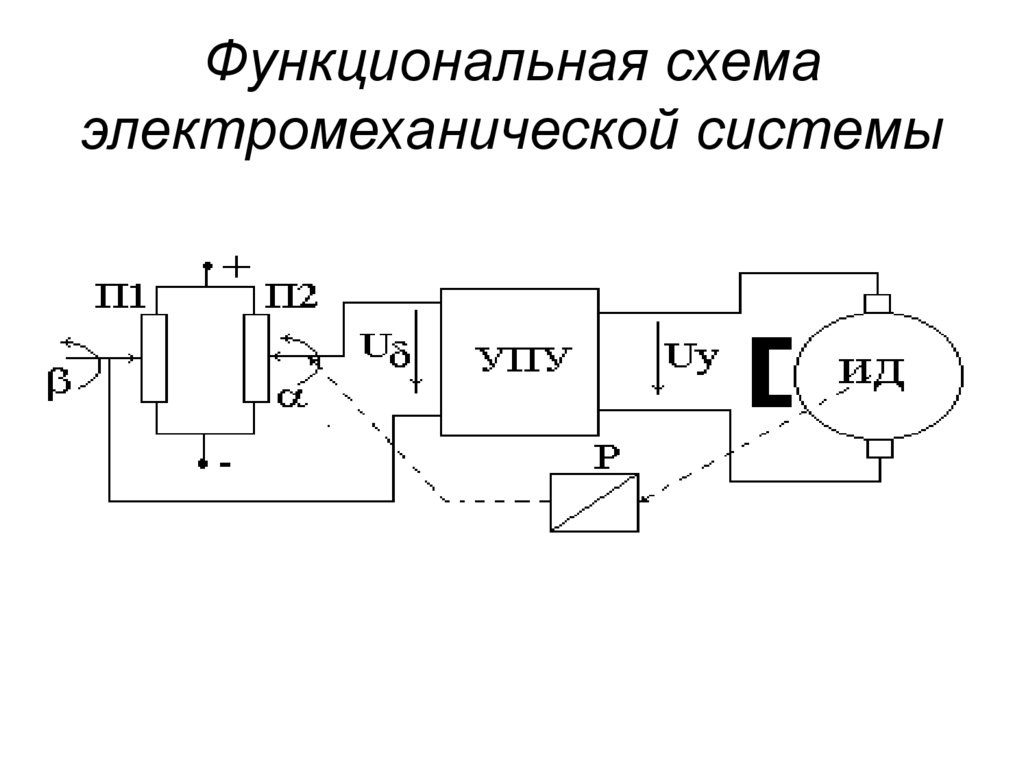
7. Функциональная схема электромеханической системы
8.
Система имеет типичный набор элементов.К ним, в данном случае, можно отнести:
измеритель
рассогласований
(ИР),
представленный
в
виде
потенциометрического моста П1-П2;
усилительно-преобразовательное
устройство (УПУ);
исполнительное
устройство,
электродвигатель постоянного тока с
магнитоэлектрическим возбуждением;
передаточный механизм, редуктор.
9. Математическое описание рассматриваемой системы.
• Напряжение на выходе усилительногокаскада, исходя из предположения, что
это звено безынерционное, запишется в
виде:
U y k уU .
10.
• Уравнение электрического равновесиядля
обмотки
якоря
двигателя
постоянного тока
dia
U y R a i a La
ce
dt
• Уравнение механического равновесия
d
'
J
M вр M н
dt
'
11.
• Уравнение, связывающее угол поворотавала двигателя с угловой скоростью:
д dt
• Решая
в
операторной
форме
приведенные
уравнения
можно
получить следующее равенство
1
k дU y ( TЭTM p TM p 1 ) ( 1 TЭ p )M
Fi
2
12.
где ТЭ = La/Ra – электромагнитнаяпостоянная времени, характеризующая
нарастание
скорости
момента
в
заторможенном двигателе;
F = сесм/Ra – коэффициент демпфирования,
определяющий
наклон
(жесткость)
механической характеристики;
ТМ – механическая постоянная времени,
характеризующая нарастание скорости и
определяемая
механическими
параметрами ИД:
13. Вывод
• Таким образом, в зависимости отзадачи исследований и принятых при
этом допущениях, разрабатываются
структурные схемы и математическая
модель
системы
на
базе
представленных выше уравнений.
• В данном случае структурная схема
(модель) имеет следующий вид:
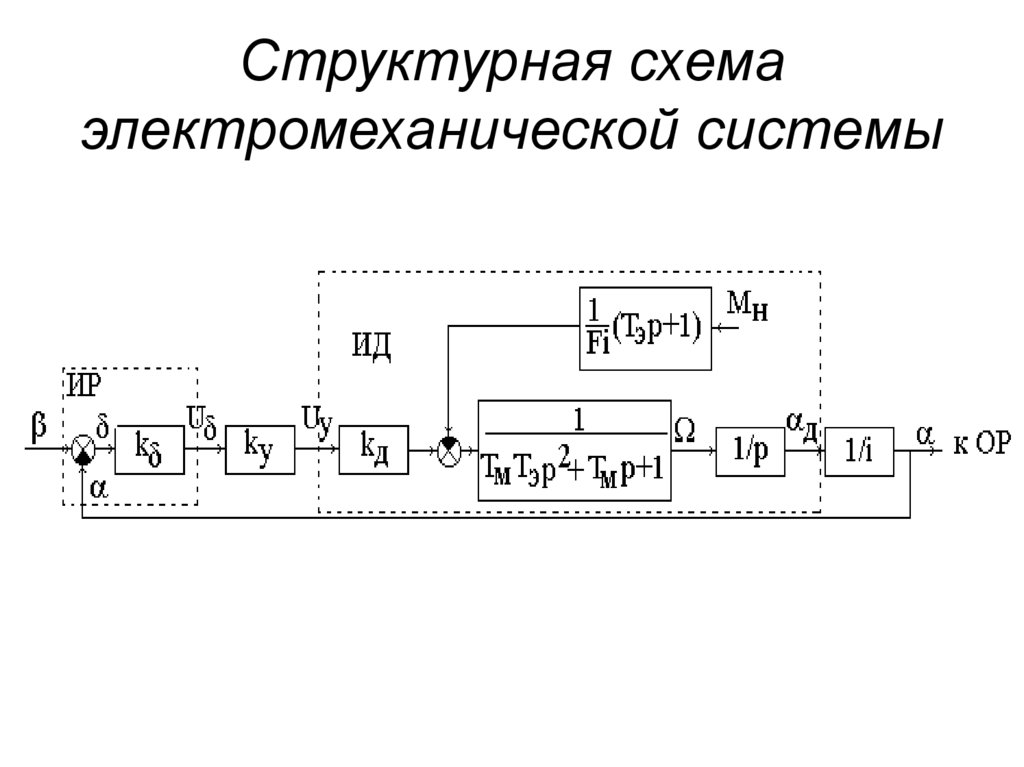
14. Структурная схема электромеханической системы
15.
• В структурной схеме исполнительныйдвигатель представлен колебательным
звеном.
• Передаточную функцию разомкнутой
системы можно записать в виде:
K
Wр ( p)
;
p(TэTм p 2 Tм p 1)
16.
где К – коэффициент передачи (добротности)системы:
K k у kд k k
k у kд k k
–
коэффициент
усиления усилителя, коэффициенты передачи
двигателя, измерителя рассогласования и
редуктора, соответственно.
17. Передаточная функция замкнутой системы
Передаточную функцию замкнутой системыопределяют по выражению:
Wз ( p)
Wр ( p)
1 Wр ( p)
.
18.
Тогда передаточная функция замкнутойсистемы по управляющему воздействию
будет иметь вид:
Wз ( p)
K
3
2
(TэTм p Tм p p) K
.
Знаменатель
передаточной
функции
является характеристическим уравнением
замкнутой системы
19. Перечень исследований с помощью передаточных функций
1.По траектории корней характеристическогоуравнения, (корневого годографа) на
комплексной плоскости можно провести
количественную и качественную оценку
влияния параметров системы на ее
устойчивость, качество регулирования и
осуществить
синтез
корректирующих
звеньев
20.
2.Используя передаточную функцию
ошибки системы по управляющему
воздействию
1
G ( p)
1 Wp ( p)
и
передаточную
системы
по
воздействию
функцию
ошибки
возмущающему
1
(Tэ p 1)
2
Fi
Y ( p)
.
Μ н (TэTм p 3 Tм p 2 p ) K
21.
можнооценить
точность
отработки
системой управляющего и возмущающего
воздействий
м
3. Используя передаточные функции
замкнутой системы по управляющему и
возмущающему воздействиям, получают
уравнения для расчета внешней и
регулировочных характеристик системы в
установившемся режиме работы в виде
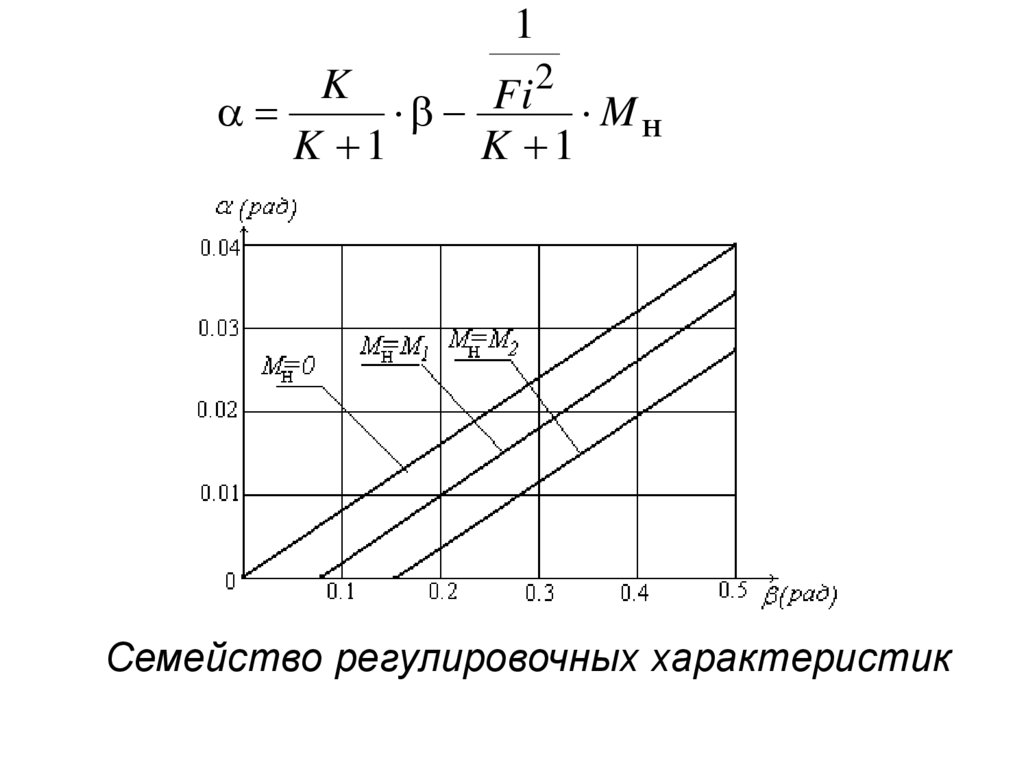
22.
12
K
Fi M н
K 1
K 1
Семейство регулировочных характеристик
23.
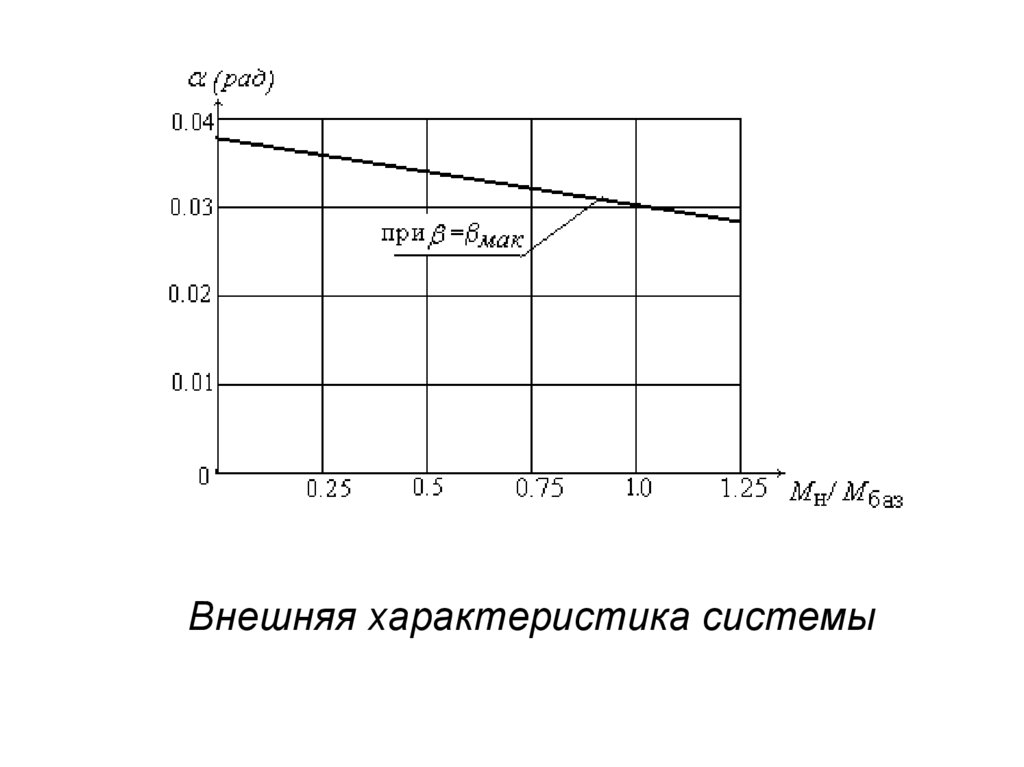
Внешняя характеристика системы24.
4.Передаточные
функции
систем
позволяют рассчитать их переходные
характеристики, анализируя которые
определяют динамические показатели
качества системы, именно:
перерегулирование σ%,
число колебаний n,
время переходного процесса tпп,
декремент затухания процесса
25. Исследование электромеханических систем в частотной области
• Проектирование, анализ и синтез систем cпомощью
частотных
характеристик
осуществляют при наличии передаточной
функции
замкнутой
(разомкнутой)
системы.
• Для
формирования
частотных
характеристик
необходимо
от
передаточной функции системы перейти к
ее частотной передаточной функции.
26. Частотная передаточная функция разомкнутой системы
KWр ( p)
;
2
p(TэTм p Tм p 1)
K
WР ( j )
2
j (TЭT ( j ) T j 1
27. Частотная передаточная функция замкнутой системы
Wз ( p)K
3
2
(TэTм p Tм p p) K
.
K
WЗ ( j )
3
2
(TЭT ( j ) T ( j ) j ) K
28. Преобразование частотных передаточных функций
• В результате преобразования частотныхпередаточных
функций
выделяют
вещественную и мнимую составляющие
функций.
• Для
этого комплексное значение
знаменателя частотной передаточной
функции умножают на сопряженное
комплексное число.
29.
•Осуществив преобразования, частотнуюпередаточную функцию приводят к виду
W ( j ) U ( ) jV ( ),
U ( ), V ( )
где
– вещественные и
мнимые частотные функции, а их
графики, соответственно, вещественная и
мнимая частотные характеристики.
•Амплитудную
и
фазовую
частотные
функции определяют по выражениям
30.
A( ) U ( ) V ( )2
2
V ( )
( ) arctq
k ,
U ( )
где k = 0, ±1, ±2,…..
31. Частотные характеристики электромеханической следящей системы
• Вещественная частотная характеристикаKT
U ( ) 2 4
.
3
2
T ( T TЭ )
2
• Мнимая частотная характеристика
K ( T TЭ )
V ( ) 2 4
.
3
2
T ( T TЭ )
3
32. Устойчивость системы
Система считают устойчивой, если•после снятия воздействия по окончанию
переходного
процесса
система
возвращается в исходное равновесное
состояние;
•после
изменения
воздействия
на
постоянную величину по окончанию
переходного процесса система приходит
в новое равновесное состояние.
33. Условия устойчивости
•Переходный процесс в любой системеопределяется свободной и принужденной
составляющими.
•Основной
составляющей,
которая
определяет
переходный
процесс
является
свободная
составляющая,
изменение которой во времени зависит
от
корней
характеристического
уравнения системы
34.
Всамом
общем
случае
корни
характеристического уравнения – это
комплексные сопряженные числа
pi ,i 1 ai j i
где ai может быть положительной или
отрицательной величиной.
При этом если ai 0
, свободная
составляющая будет затухать и наоборот,
ai 0
при
получаются расходящиеся колебания
35. Вывод
• Отсюда следует, что общим условиемзатухания
всех
свободных
составляющих,
а
значит,
всего
переходного процесса в целом является
отрицательность вещественных частей
всех полюсов передаточной функции
электромеханической системы
36. Критерии устойчивости системы
Устойчивость системы оценивают с помощьюследующих критериев устойчивости:
• критерий устойчивости Гурвица;
• критерий устойчивости Михайлова;
• критерий устойчивости Найквиста.
37. Критерий устойчивости Найквиста
• Для исследования устойчивости системы вдинамических
режимах
работы
широко
используют критерий Найквиста, основанный
на
построении
частотного
годографа
разомкнутой системы.
• Для
устойчивости
замкнутой
системы
автоматического
управления
(САУ)
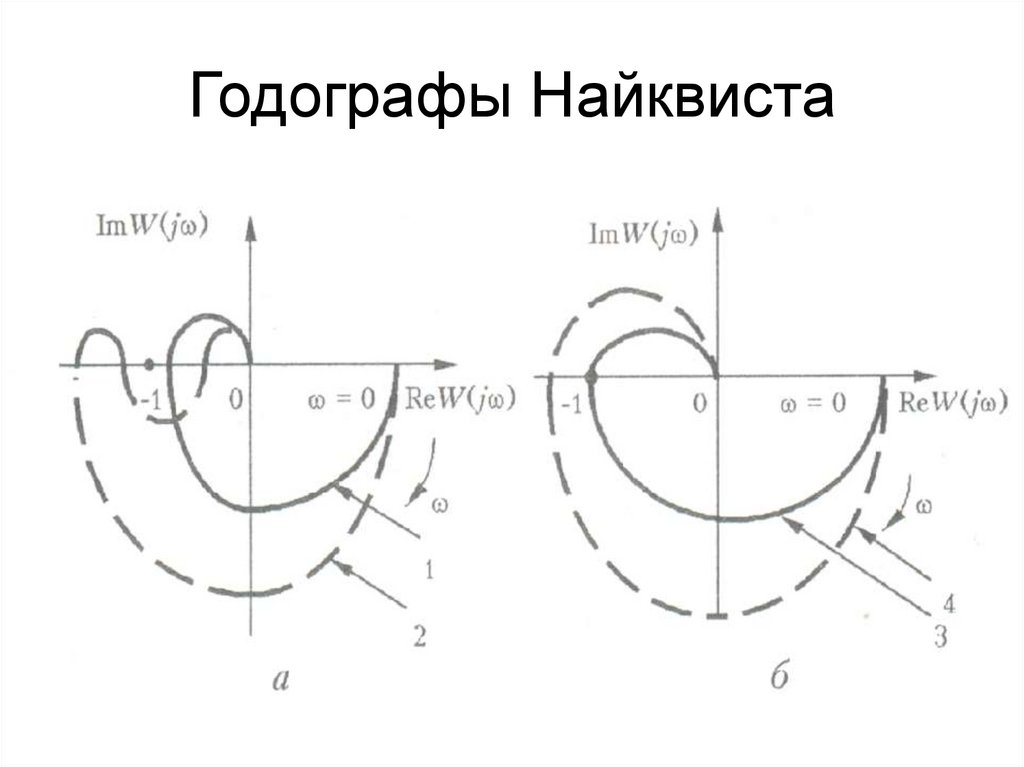
необходимо и достаточно, чтобы годограф
Найквиста при изменении частоты от 0 до
не охватывал точку с координатами ( 1, j 0).
38. Годографы Найквиста
39. Метод логарифмических амплитудно-фазовых частотных характеристик
• В инженерной практике расчета ипроектирования
систем
автоматического
управления,
электромеханических систем и систем
электронной
техники
широко
применяется метод логарифмических
амплитудно-фазовых
частотных
характеристик (ЛАФЧХ).
40.
• В этом случае частотные характеристикистроятся на полулогарифмической сетке,
когда по оси абсцисс откладывается частота
в логарифмическом масштабе, а по оси
ординат амплитуда в децибелах, а фаза в
радианах:
L 20 log A ;
• Бел представляет собой логарифмическую
единицу, соответствующую десятикратному
увеличению мощности. Децибел равен 0,1
Бел.
41.
• частотнаяпередаточная
функция
представляет собой отношение не
мощностей, а выходной и входной
величин,
то
увеличение
этого
отношения
в
десять
раз
будет
соответствовать увеличению отношения
мощностей в 100 раз, что соответствует
2 Белам или 20 дб. Поэтому в правой
части уравнения имеем множитель 20
42. Суть метода логарифмических частотных характеристик
•Суть этого метода сводится к анализулогарифмических частотных характеристик
разомкнутых систем.
•В результате анализа оцениваются такие
показатели качества системы, как: запас
устойчивости замкнутой системы по фазе и
амплитуде,
точность
отработки
управляющих сигналов, частотный диапазон
работы, колебательность и быстродействие
системы.
43.
•Метод ЛАФЧХ позволяет произвестисинтез системы в соответствии с
требованиями технического задания.
•Для
этого
в
базу
данных
на
моделирование
необходимо
ввести
подпрограмму для типовых желаемых
логарифмических
амплитудных
и
фазовых характеристик.
•Провести
сравнительный
анализ
логарифмических
характеристик
неизменной части разомкнутой системы с
желаемыми
логарифмическими
характеристиками.
44.
• произвестисинтез
корректирующих
звеньев;
• получить
характеристики
спроектированной в соответствии с
требованиями технического задания (ТЗ)
системы.
45. Построения логарифмических амплитудно-фазовых частотных характеристик
• Рассмотримпример
построения
логарифмических
амплитудно-фазовых
частотных
характеристик
следящей
системы, в неизменную часть которой
входят интегрирующее, апериодическое и
колебательное звено.
W p
K
2 2
p T1 p 1 T2 p 2 T2 p 1
46. Частотные характеристики системы
•Заменив в передаточной функцииp = j , получают частотную передаточную
функцию
W j
K
j T1 j 1 1 T2 j 2 T
2
47.
• Амплитуда А( ) частотнойпередаточной функции в данном случае
имеет вид
A
1 T 2 2
K
2
2
2 2
1 T2
2 T2
• а фазовая функция
2 2
arctg 1 arctg
2 2
2
1
2
48.
•При использовании системы MathCADдля расчета и построения точных
логарифмических
частотных
характеристик пользуются выражением
L1 : 20log A
•Асимптотическая
логарифмическая
амплитудная частотная характеристика
рассчитывается
с
использованием
функции if,
49.
• В рассматриваемом случае расчеттакой характеристики представлен в
виде следующего набора выражений
L0 : 20log K 20lоg
L : if 1 ,0, 20log
1
1
T1
1
L2 : if ,0, 40log 2
T2
L : L L L
0
1
2
: 1,1.5,..100
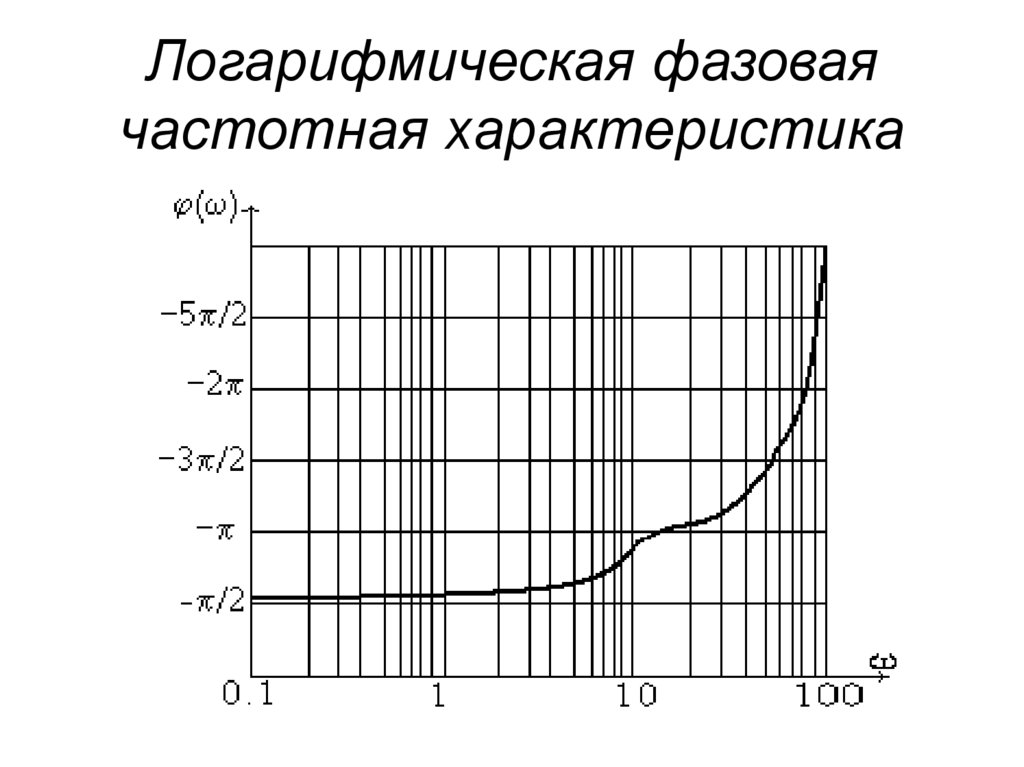
50. Фазовая частотная характеристика в данном случае рассчитывается по выражению:
2 2: atan 1 atan
2 2
2
1 2
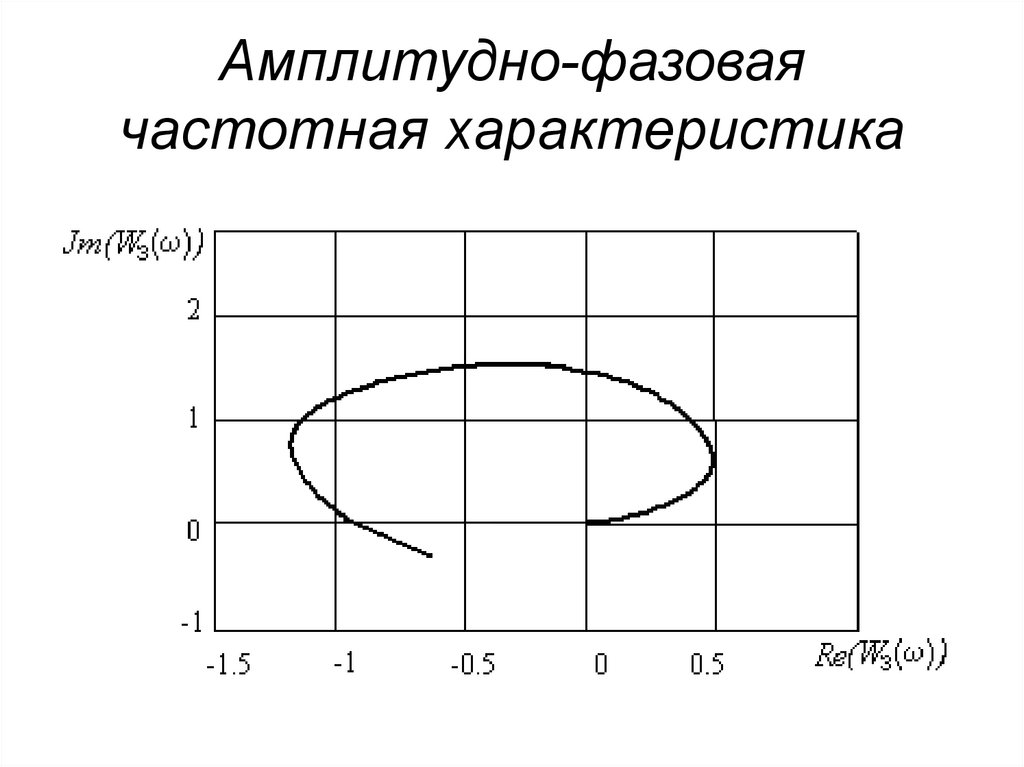
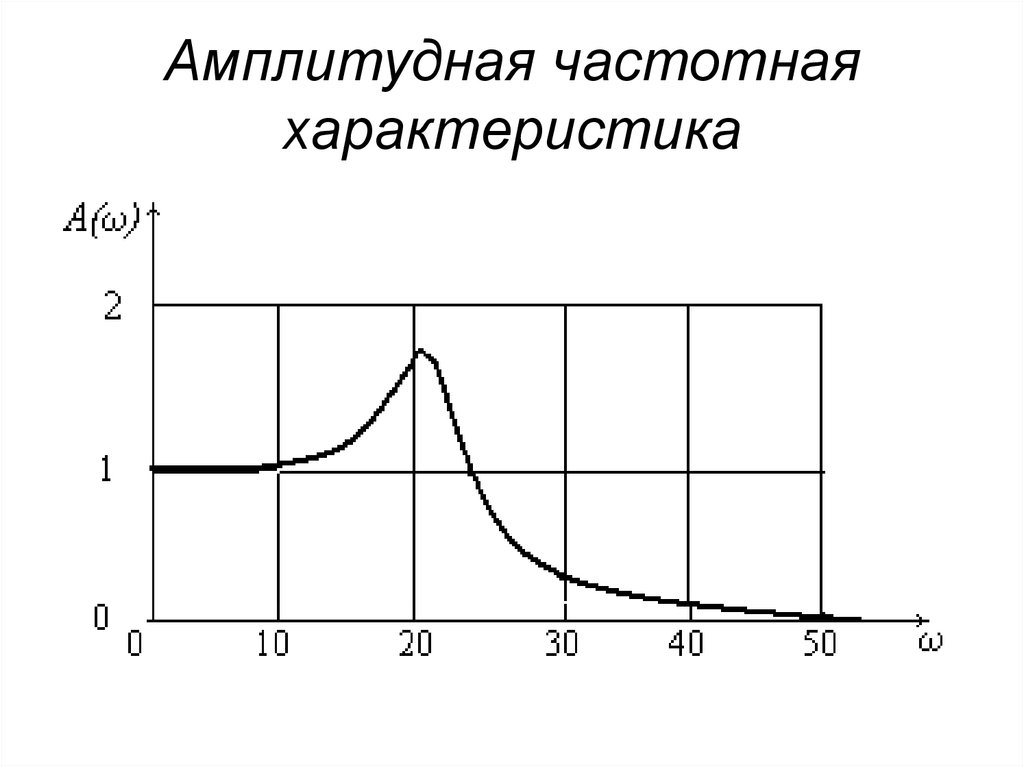
Результаты расчетов при исходных
данных
T 2 : 0.08; T1 : 0.15; K : 100; : 0.15
имеют следующий вид























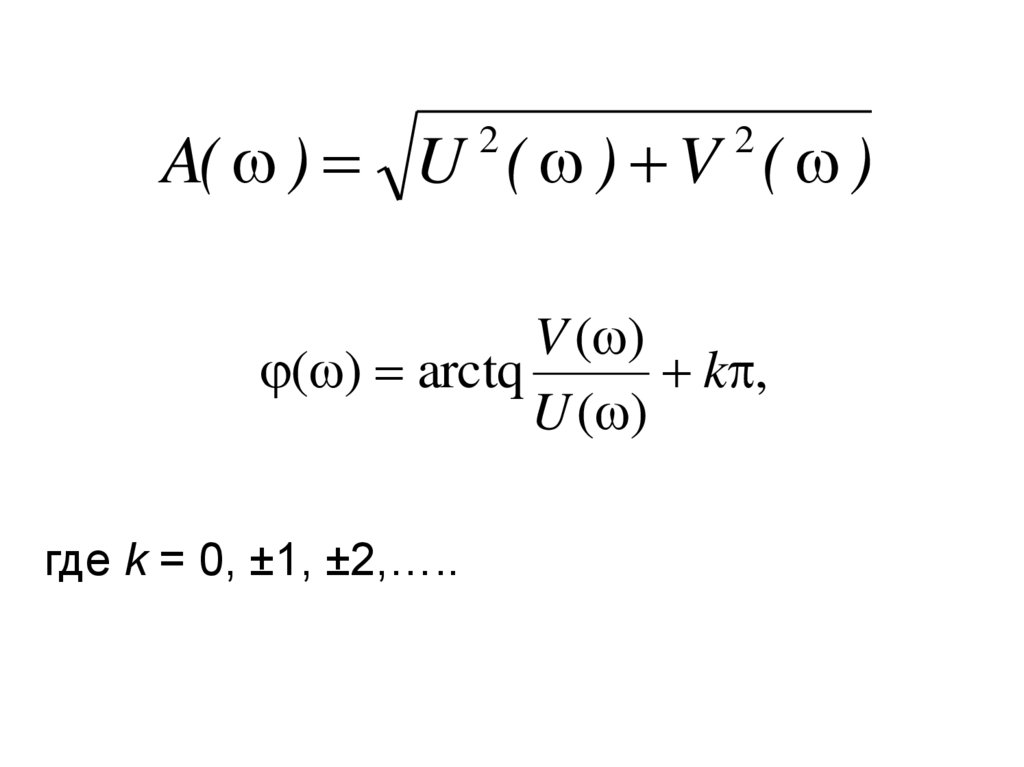




















 Физика
Физика








