Похожие презентации:
Отношения и предикаты. (Лекция 7)
1. Отношения. Предикаты
12. Отношения
• Определение 1R A1 A2 ... An
а) Множество
называется n-местным
отношением между элементами множеств А1,А2,...,Аn;
Пусть
R A1 A2 ... An
а) При n=1 R A1
свойством;
Определение 2
– n – местное отношение.
называется одноместным отношением или
б) при n=2 R A1 A2 называется двухместным отношением или
бинарным отношением или просто отношением;
2
3. Примеры
• 1) M={сентябрь, февраль, январь}, R MR x | x зимний месяц
• 2)
R январь, февраль
A 2;4;5;6
R A2 , R ( x, y ) | НОД ( x, y ) 1
R (2;5), (5;2), (4;5), (5;4), (5;6), (6;5)
• 3) B={Толстой, Достоевский, Пушкин}
С={Идиот, Аэлита, Овод, Братья Карамазовы}
R B C, R ( x, y) | x автор y
R={(Толстой, Аэлита),(Достоевский, Идиот), (Достоевский, Братья
Карамазовы) }
4) X={
,
,
}, Y={2,3,4,5,6}
R X Y , R ( x, y) | y число вершин x
R={(
,4),(
,6),(
,3)}
3
4. Предикаты
Каждому отношению можно поставить в соответствие некотороелогическое выражение PR, зависящее от n переменных (nместный предикат) и определяющее, будет ли кортеж
принадлежать отношению R . Это логическое выражение
называют предикатом отношения.
a1, a2 ,..., an R
PR a1, a2 ,..., an 1
a1, a2 ,..., an R
PR a1, a2 ,..., an 0
4
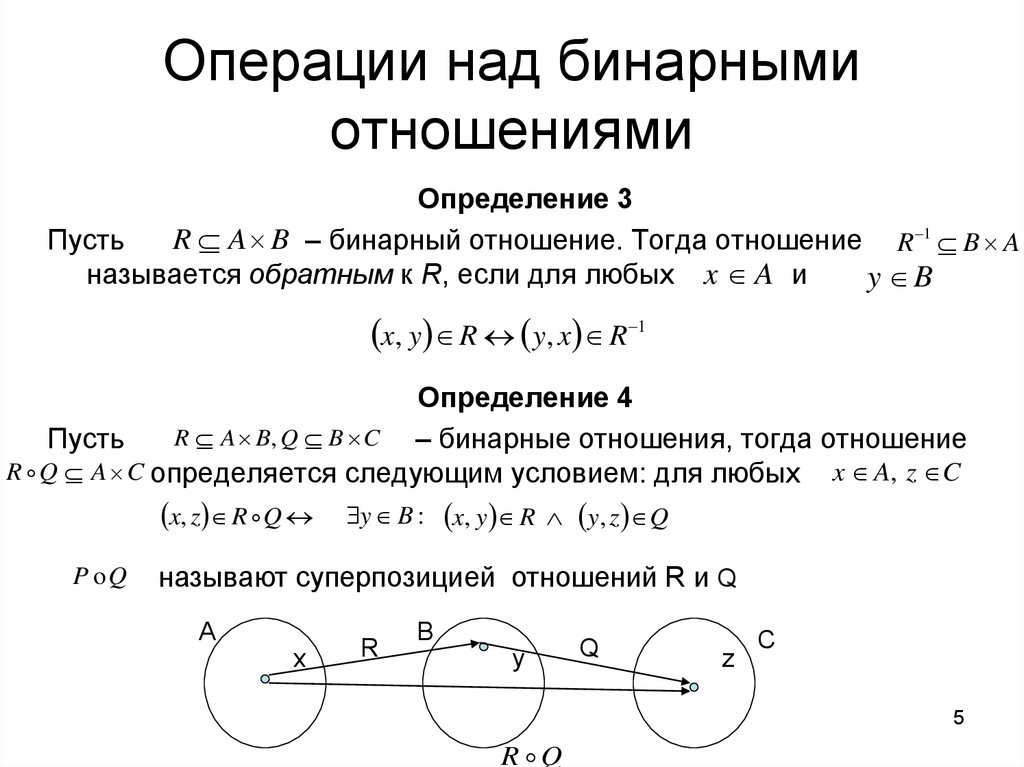
5. Операции над бинарными отношениями
Определение 3R A B – бинарный отношение. Тогда отношение R 1 B A
Пусть
называется обратным к R, если для любых x A и
y B
x, y R y, x R 1
Определение 4
R A B, Q B C – бинарные отношения, тогда отношение
Пусть
R Q A C определяется следующим условием: для любых x A, z C
x, z R Q
P oQ
y B :
x, y R
y, z Q
называют суперпозицией отношений R и Q
A
x
R
B
y
Q
z
C
5
R Q
6. Примеры
A={1,2,3},B={a, b, c},C={x, y, z};
R={(1;a);(1;c);(2;b);(2;c);(3;a)} A B
Q={(a; x);(a; y);(b; y);(b; z);(c; x);(c; z)} B C
R 1 ?
• R-1={(a;1);(c;1);(b;2);(c;2);(a;3)}
R Q ?
• R Q ={(1;x);(1;y);(1;z);(2;x);(2;y);(2;z);(3;x);(3;y)}=
= ( A C )\{(3;z)}.
1
a
2
x
b
3
y
c
R
z
Q
6
7. Матрица отношения
• Определение 5
Матрицей бинарного отношения R A B называют матрицу
, где
[ PR ] ( pij ) m n
1, если ( ai , b j ) R,
pij
0, если ( ai , b j ) R.
Пример
Q 1 {( x; a); ( x; c); ( y; b)}
A={1,2,3},B={a, b, c},C={x, y};
R={(1;a);(1;c);(2;b);(3;a)}
A C {(1; x ); ( 2; x ); (3; x ); (1; y ); ( 2; y ); (3; y )}
Q={(a; x);(b; y);(c; x)}
R Q {(1; x ); (2; y ); (3; x )}
a
1 1
[ PR ]
2 0
3 1
b c
0 1
1 0
0 0
x y
a 1 0
[ PQ ]
0
1
b
c 1 0
a b c
1
Q
[P ] x 1 0 1
y 0 1 0
x
[ PR Q ]
1
2
3
y
1 0
0
1
1 0
7
8. Операции над отношениями в матричном виде
R, Q A B, [ PR ] ( rij )m,n , [ PQ ] ( qij )m,nПусть
1)
[ PR Q ] ( rij qij )
2)
[ PR Q ] ( rij qij )
3)
[ PR \Q ] ( rij qij )
4)
Пусть
5)
,тогда
1
[ PR ] [ PR ]Т
R A B, Q B C
, тогда
[ PR Q ] ( rik qkj )
k
8
9. Пример
Дано:Найти
A {a1 , a2 , a3}, B {b1 , b2 }
R Q, R Q, Q \ R, Q 1, R Q 1
R {( a1, b1 ), (a1, b2 ), (a2 , b2 ), (a3 , b1 )},
Q {( a1 , b1 ), (a2 , b2 ), (a3 , b2 )}
Решение:
PR
b1 b2
PQ
b1 b2
a1
a2
1
0
1
1
a1
a2
1
0
0
1
a1
a2
1
0
1
1
1
0
0
1
0
0
1
0
a1
a2
0
0
a3
a1
a2
a3
0
1
a3
1
1
a3
0
0
a3
0
1
a1 a2
a3
a1
a2
1
0
1
1
1
1
a3
1
0
0
PQ
1
a1 a2
a3
b1
1
0
0
b2
0
1
1
PR Q
PR Q 1
b1 b2
PR Q
b1 b2
PQ \ R
b1 b2
1 0 1 1 1
9








 Математика
Математика








