Похожие презентации:
Нормальный закон распределения
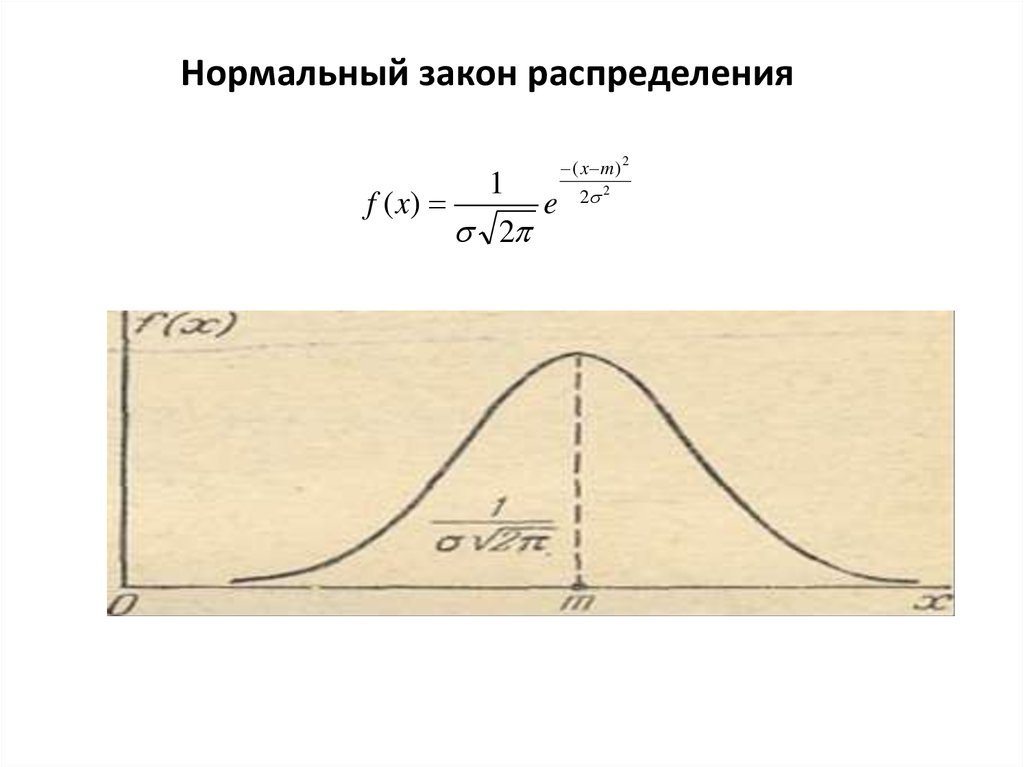
1. Нормальный закон распределения
f ( x)1
2
( x m)2
e
2 2
2. Нормальный закон распределения
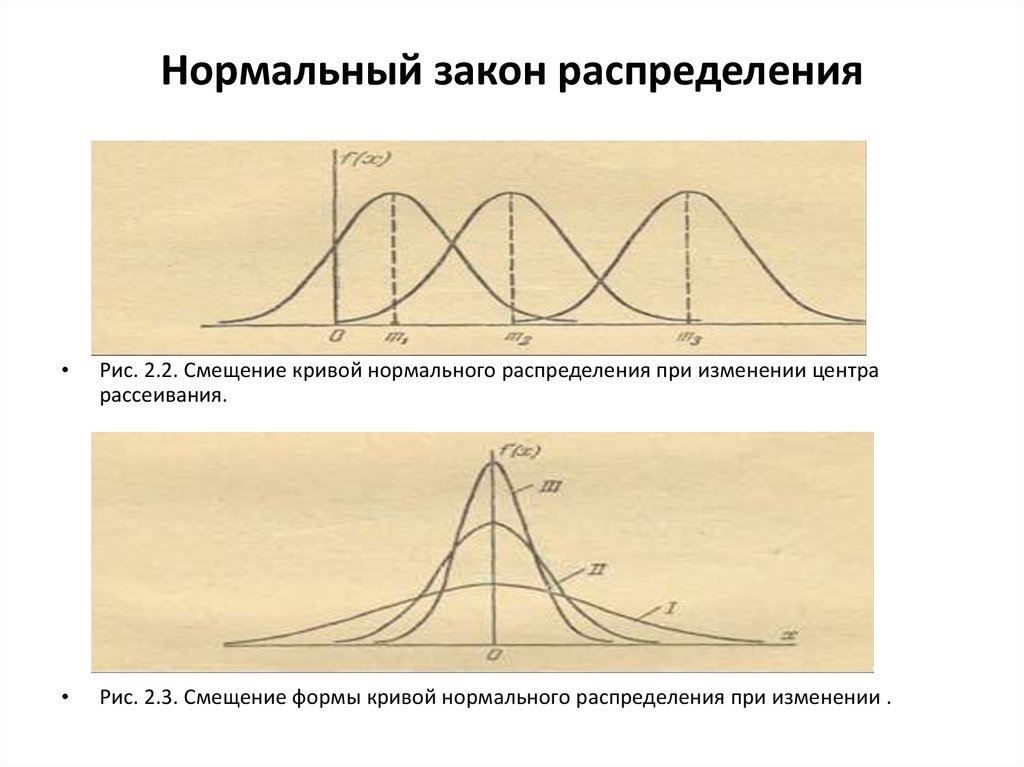
Рис. 2.2. Смещение кривой нормального распределения при изменении центра
рассеивания.
Рис. 2.3. Смещение формы кривой нормального распределения при изменении .
3. Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок.
4. Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Как и всякая функция
распределения, функция Ф(х) обладаетсвойствами:
1. Ф( ) = 0.
2. Ф( ) = 1.
3. Ф(х) - неубывающая функция.
Кроме того, из симметричности нормального распределения
с параметрами m = 0, = 1 относительно начала координат
следует, что
Ф( x) 1 Ф( x)
5. Правило «трех сигма»
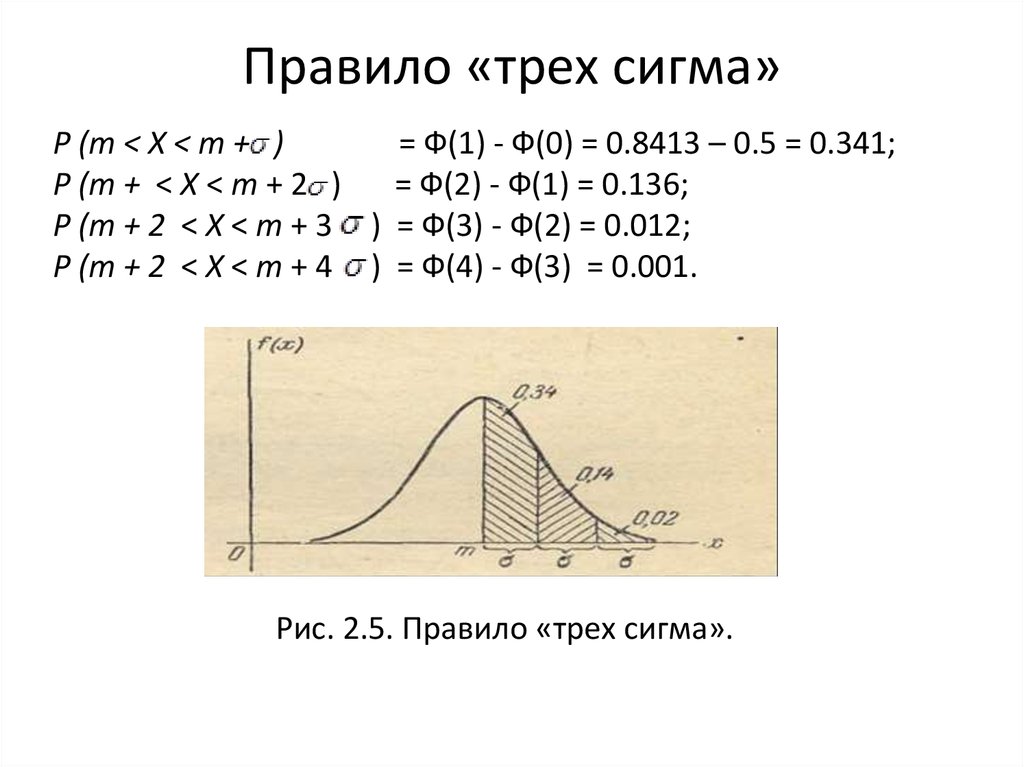
Р (т < X < т + )= Ф(1) - Ф(0) = 0.8413 – 0.5 = 0.341;
Р (т + < X < т + 2 )
= Ф(2) - Ф(1) = 0.136;
Р (т + 2 < X < т + 3 ) = Ф(3) - Ф(2) = 0.012;
Р (т + 2 < X < т + 4 ) = Ф(4) - Ф(3) = 0.001.
Рис. 2.5. Правило «трех сигма».
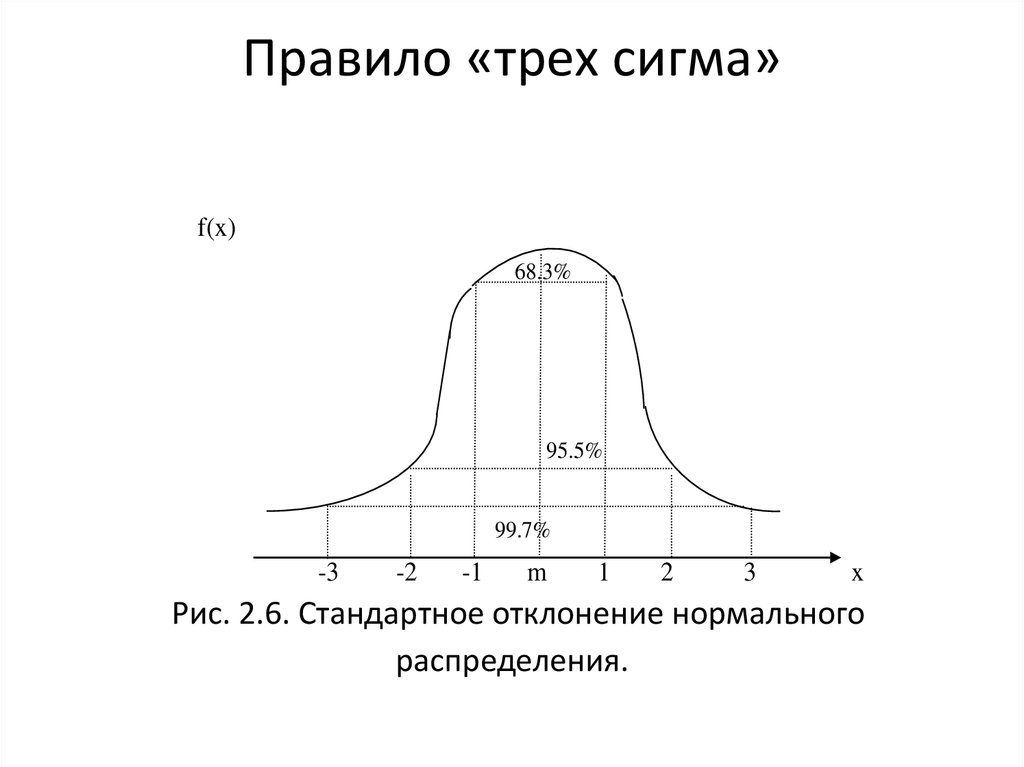
6. Правило «трех сигма» Рис. 2.6. Стандартное отклонение нормального распределения.
Правило «трех сигма»f(x)
68.3%
95.5%
99.7%
-3
-2
-1
m
1
2
3
x
Рис. 2.6. Стандартное отклонение нормального
распределения.
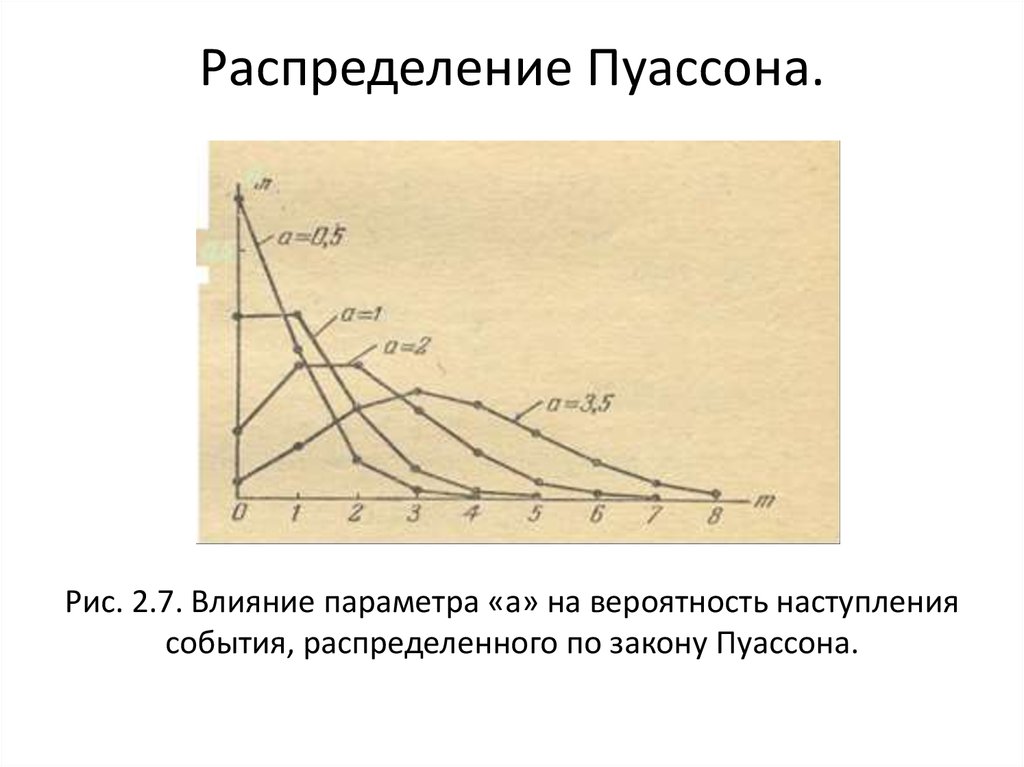
7. Распределение Пуассона.
a m aPm
e
m!
(m = 0, 1, 2, …)





 Математика
Математика








