Трассировка лучей

1. Трассировка лучей

Будак Владимир Павлович,
НИУ «МЭИ»
кафедра светотехники
: +7 (095) 763-5239
[email protected]

2. Необходимые пояснения

В литературе по компьютерной графике так часто встречается сочетание Ray
Tracing, что создается впечатление, что все сделано этим Рэем Трейсингом.
Медведев В.Е., Парицкая Г.Г. Расчет освещенности в изображении // Оптика и
спектроскопия, 1966. Т.22, N5. - С.638-642.
Кущ О.К., Митин А.И. Расчет светораспределения зеркальных симметричных
поверхностей с протяженным источником света на ЭВМ //Светотехника, 1976.
N6. - С.3-5.
Коробко А.А., Кущ О.К. Использование метода Монте-Карло в светотехнических расчетах // Светотехника,1986. N10.-С.14-17.
Кущ О.К. Оптический расчет световых и облучательных приборов на ЭВМ.М.: Энергоатомиздат, 1991. - 150С.
Программа энергетического расчета TracePro
Представляет собой метод решения полного уравнения
глобального освещения

3. Ряд Неймана

1
(r; ˆl , ˆl ) F (r, r ) (r, r )
2
L(r, l ) L0 (r, l ) L(r , l ) (r; l, l ) F (r, r ) (r, r ) d r , k (r r )
Для простоты дальнейших рассуждений представим уравнение в виде
L(r, ˆl ) L0 (r, ˆl ) L(r , ˆl ) k (r r ) d 2 r L0 K L,
2
k
(
r
r
)
d
r 1
Если норма ядра | | 1, то решение интегрального уравнения в
выбранном пространстве представимо в виде ряда Неймана
von Neumann, 1903 - 57, родился Будапешт, работал в
Германии, США, Лос Аламос, метод Монте-Карло
L(r, l ) n K n L0
n 0
Физически ряд Неймана представляет разложение яркости по
кратностям переотражений от поверхностей сцены

4. Геометрическая интерпретация ряда Неймана

1
L(r, ˆl ) L0 (r, ˆl ) L0 (r1 , ˆl1 ) (r; ˆl, ˆl1 ) F (r, r1 ) (r, r1 ) d 2 r1
1
L(ri , ˆli ) L0 (ri , ˆli ) L0 (r j , ˆl j ) (ri ; ˆli , ˆl j ) F (ri , r j ) (ri , r j ) s j
j
ˆ , ˆl )(N
ˆ , ˆl )
1
(
N
L(ri , ˆli ) L0 (ri , ˆli ) L(r j , ˆl j ) (ri ; ˆli , ˆl j ) (ri , r j ) j , F (r, r )
j
(r r ) 2
Построение луча возможно двумя способами:
• от источника к камере – прямой ход
• от камеры к источнику – обратный ход
Оба метода имеют свои достоинства и недостатки, но при однократном
отражении обратный ход эффективнее

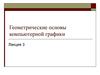
5. Координаты луча

Луч характеризуется точкой выхода и направлением.
Точка выхода луча r:
• прямой ход из источника
• обратный ход из точки (пикселя) изображения
плоскость
изображения
ˆl ro ri , r x, y, z ,
ro ri
оптическая
система
ri
ro
ro ri xo xi , yo yi , zo zi ,
r
ro ri ( xo xi ) 2 ( yo yi ) 2 ( zo zi ) 2
rs
Уравнение луча
r ( ) ro ˆl , r ro , ˆl
O
Сцена
Следующий этап – определение точки пересечения луча с поверхностью
либо источника, либо объекта сцены

6. Пересечения луча с поверхностью

Если поверхность задается уравнением F(r)=0, то
координаты точки пересечения есть решение системы
уравнений
F (ro ˆl ) 0 rs ro 0 ˆl
r ro ˆl ,
F (r ) 0.
Пример №1: пересечение с плоскостью
ˆ
ro rp , N
ˆ 0 0
ˆ 0 ro ˆl rp , N
r rp , N
ˆl , N
ˆ
Пример №2: пересечение со сферой
(r rc ) 2 R 2
2
ˆl, r r ) (r r )2 R2 0
2
(
o
c
o
c
2
2
ˆ
(ro l rc ) R
(ˆl, r r ) (ˆl, r r ) (r r ) 2 R 2
1,2
o
c
o
c
o
c
Аналогично можно найти пересечения с простыми объектами, для сложных –
пересечение с гранями сетки, его аппроксимирующими

7. Пересечение с гранью

1. определяется координата пересечения луча с плоскостью многоугольника
2. определение принадлежности точки пересечения области многоугольника
• задача легко из трехмерной сводится к плоской:
если точка пересечения лежит внутри любой из ортогональных проекций
многоугольника, то она лежит внутри и самого многоугольника
• Исключением из правила является случай: проекция многоугольника
вырождается в отрезок - необходимо три подпрограммы для трех проекций
• Проверка принадлежности может основываться на вычислении суммы углов
между прямыми линиями, проведенными из проверяемой точки ко всем
вершинам многоугольника
Если сумма равна 0 - точка внешняя, если 2 - точка внутри многоугольника.
Диск: принадлежность определяется простым сравнением расстояния от нее до центра
Количество граней для аппроксимации реальных объектов огромно –
применяются объекты оболочки

8. Преломление луча на поверхности раздела

Закон преломления Снеллиуса (Снелль
Виллеброрд, Snellius, Snell van Royen
1580, Лейден, - 30.10.1626, там же),
sin i1 n2
sin i2 n1
i1
l1
Поскольку все три вектора l1, l2 и N лежат в одной
плоскости (компланарны)
n1
n2
i2
N
l2
ˆ , ˆl ) (N
ˆ , ˆl ) , cos i cos i ,
(N
2
1
2
1
ˆl ˆl N
ˆ
2
1
ˆ
ˆ
ˆ
ˆ
(l1 , l 2 ) (N, l1 ). cos(i1 i2 ) cos i1
n1
, cos i2 cos i1
n2
2
ˆl n1 ˆl 1 n1 1 (N
ˆ , ˆl ) 2 n1 ( N
ˆ , ˆl ) N
ˆ
2
1
1
1
n2
n2
n2
Позволяет по координатам луча сразу получать координаты преломленного
луча без использования тригонометрических функций

9. Параксиальное приближение

N
n1=1
r
R
n2=n
s
s’
l 2
C
2
n
n
n
ˆl 1 ˆl 1 1 1 (N
ˆ , ˆl ) 2 1 (N
ˆ , ˆl ) N
ˆ
2
1
1
1
n2
n2
n2
В приближении параксиальной оптики (N,l) 1 спроецируем
уравнение на плоскость перпендикулярную оптической оси:
1
1
l 2 1 N
n
n
n 1 n 1
,
s s
R
r 1 r n 1 r
s n s
n R
f
R
n 1
Соответствует формуле Гаусса (Gau ) в отрезках для преломляющей
сферической поверхности

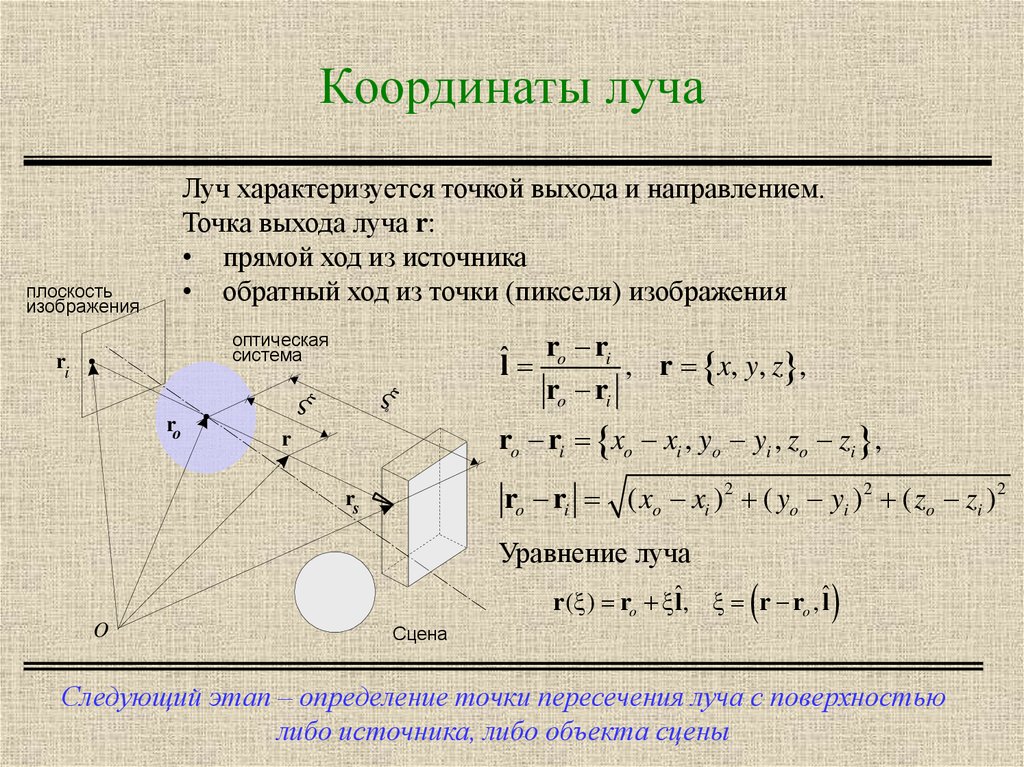
10. Стохастическая рекурсия лучей

L(r, l ) L0 (r, l )
1
2
L
(
r
,
l
)
(
r
;
l
,
l
)
F
(
r
,
r
)
(
r
,
r
)
d
r1
0 1 1
1
1
1
1
L0 (r2 , l 2 ) (r; l1 , l 2 ) F (r1 , r2 ) (r1 , r2 ) d 2 r2 (r; l, l1 ) F (r, r1 ) (r, r1 ) d 2 r1
Наилучший метод решения задачи стохастической рекурсии –
метод Монте-Карло