Похожие презентации:
Растровые алгоритмы
1. МЕТОДЫ ОБРАБОТКИ ДВУМЕРНЫХ ИЗОБРАЖЕНИЙ
Проф. Митин Александр Иванович2. Растровые алгоритмы
ЧетырехсвязностьВосьмисвязность
3. Растровые алгоритмы
Растровое представление отрезкастандартного
нестандартного
4. Растровые алгоритмы
Метод цифрового дифференциальногоанализатора (ЦДА)
y y
y y
x x
i 1
2
1
2
1
i
x
5. Растровые алгоритмы
Метод БрезенхемаОшибка
- расстояние между действительным
положением отрезка и ближайшими координатами сетки
a
b
6. Растровые алгоритмы
Метод БрезенхемаПример отрезка с
угловым
коэффициентом 3/8
(+1/4)
График ошибки
(-1/8)
(-3/4)
(-3/8)
7. Растровые алгоритмы
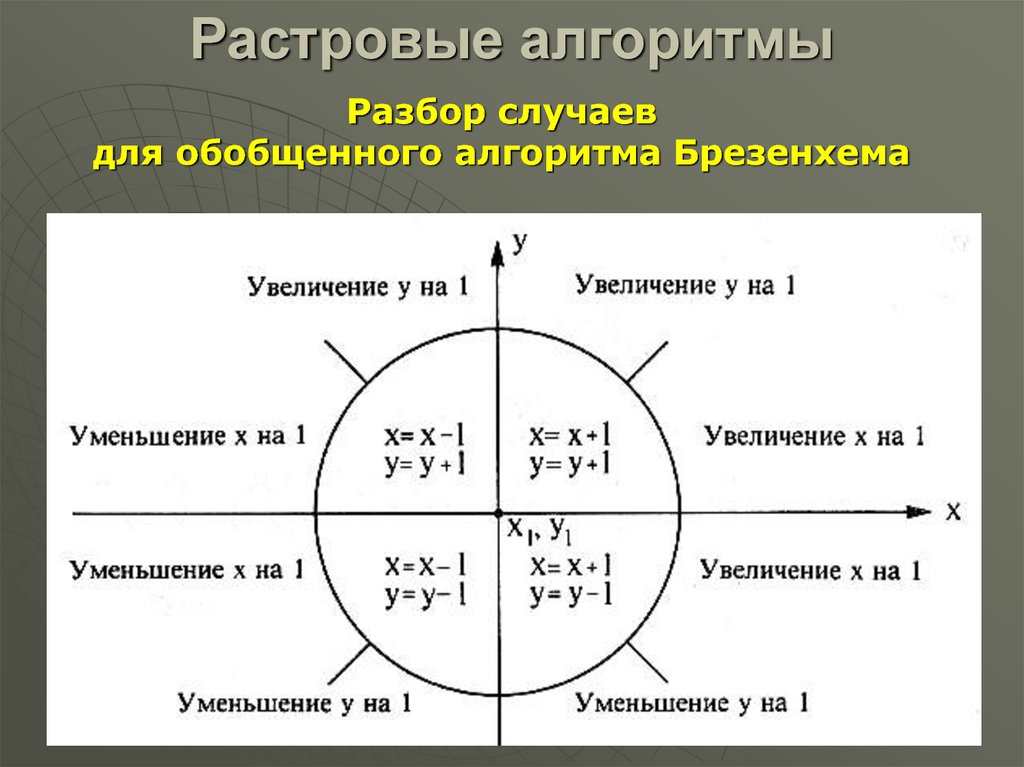
Разбор случаевдля обобщенного алгоритма Брезенхема
8. Растровые алгоритмы
Генерация полной окружности из дугив первом октанте
9. Растровые алгоритмы
Окружностьв первом
квадранте
Выбор пикселов
в первом
квадранте
10. Растровые алгоритмы
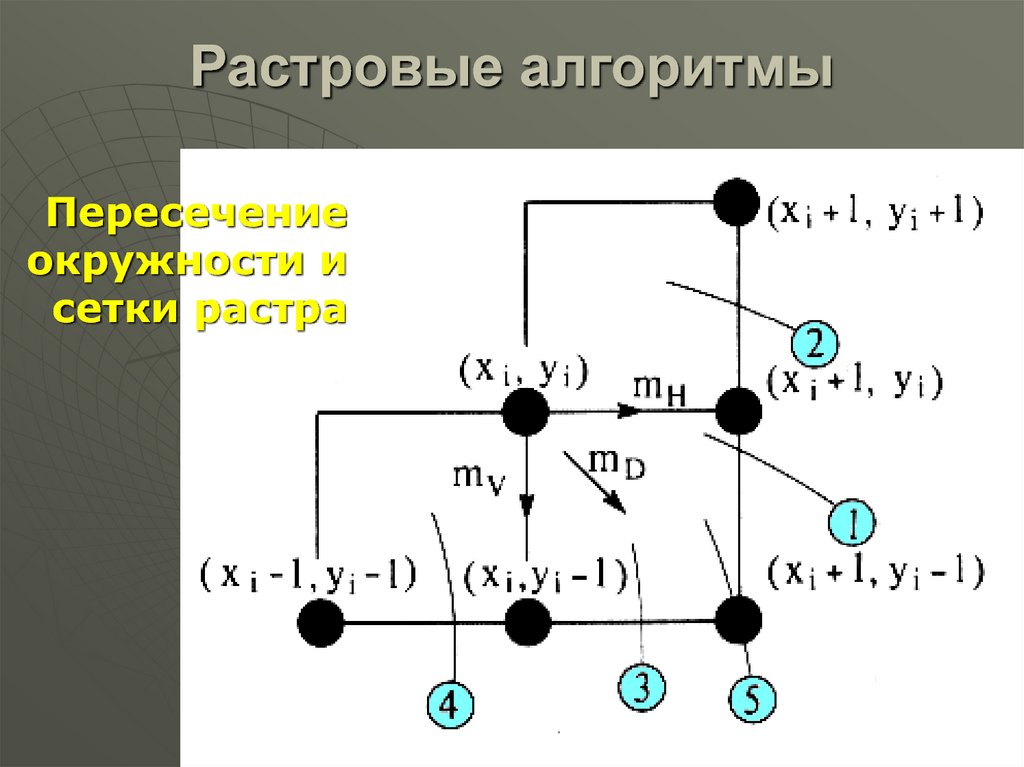
Пересечениеокружности и
сетки растра
11. Растровые алгоритмы
Результаты работы пошагового алгоритмаБрезенхема генерации окружности
12. Растровые алгоритмы
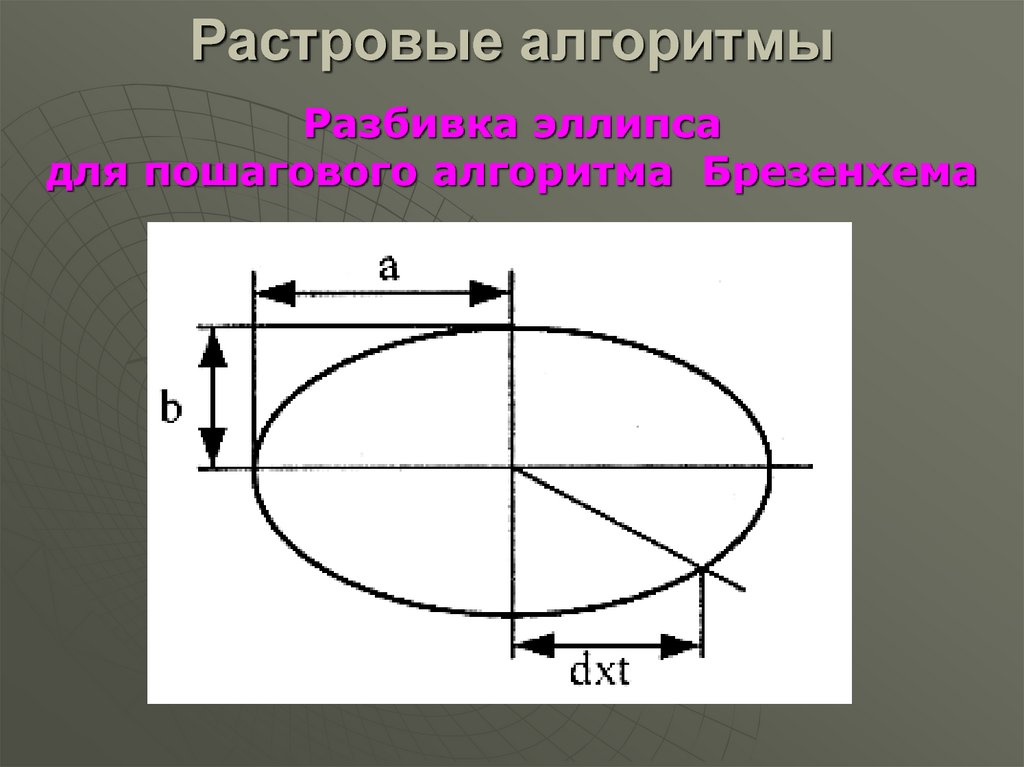
Разбивка эллипсадля пошагового алгоритма Брезенхема
13. Отсечение отрезков
Двумерное отсекающее окно14. Отсечение отрезков
Точка ЛЕВЕЕ окнаТочка ПРАВЕЕ окна
Точка НИЖЕ окна
Точка ВЫШЕ окна
Коды областей, которым
принадлежат концевые точки
15. Отсечение отрезков
P1 (-3/2, 1/6)P2 (1/2, 3/2)
P3 (-3/2, -1)
P4 (3/2, 2)
xл = -1
xп = 1
yн = -1
Простое двумерное
отсечение
yв = 1
16. Отсечение отрезков
P1 (-3/2, 1/6)P2 (1/2, 3/2)
xл = -1
xп = 1
yн = -1
yв = 1
Алгоритм Сазерленда - Коэна
17. Отсечение отрезков
Разбиениесредней
точкой
18. Отсечение отрезков
P1 (-3/2, -3/4)P2 (3/2, 1/2)
P3 (-5/2, -1)
P4 (3/2, 2)
xл = -1
xп = 1
yн = -1
yв = 1
Параметрическое отсечение
частично видимых отрезков
19. Отсечение отрезков
P1 (-1/2, 1/2)P2 (1/2, -1/2)
P3 (3/2, -1/2)
P4 (2, 1/2)
xл = -1
xп = 1
yн = -1
yв = 1
Отсечение полностью видимых и
невидимых отрезков
20. Отсечение отрезков
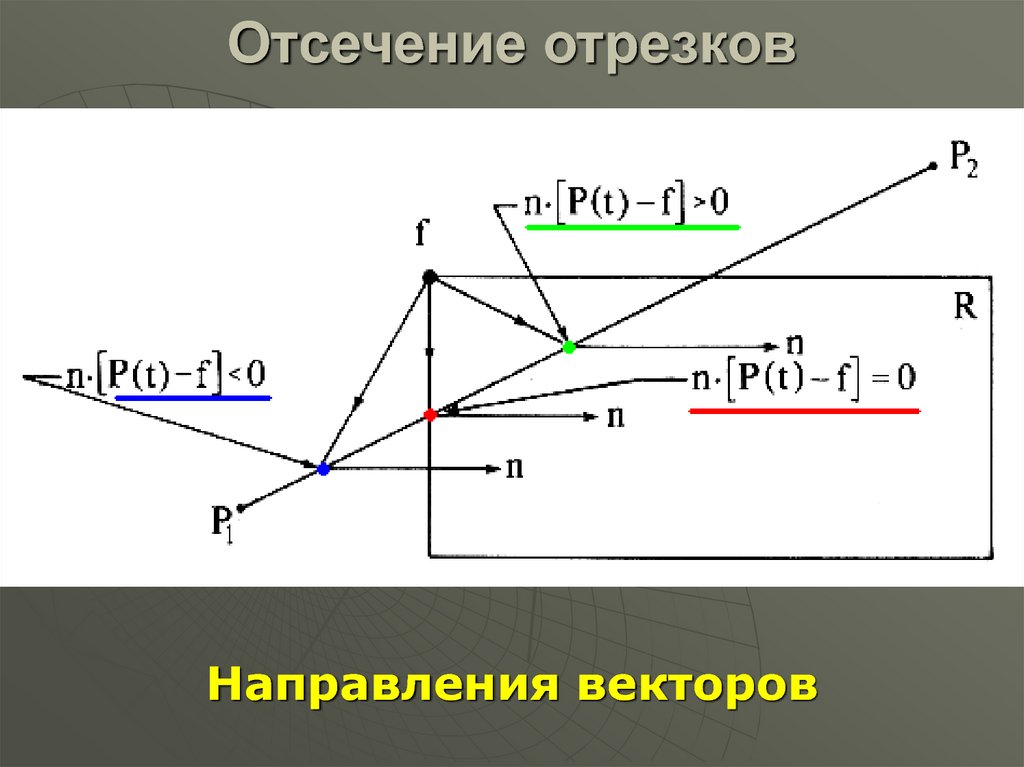
Направления векторов21. Отсечение отрезков
Отсечение Кируса – Бека:частично видимый отрезок
22. Отсечение отрезков
Отсечение Кируса – Бека:полностью видимый и невидимый отрезок
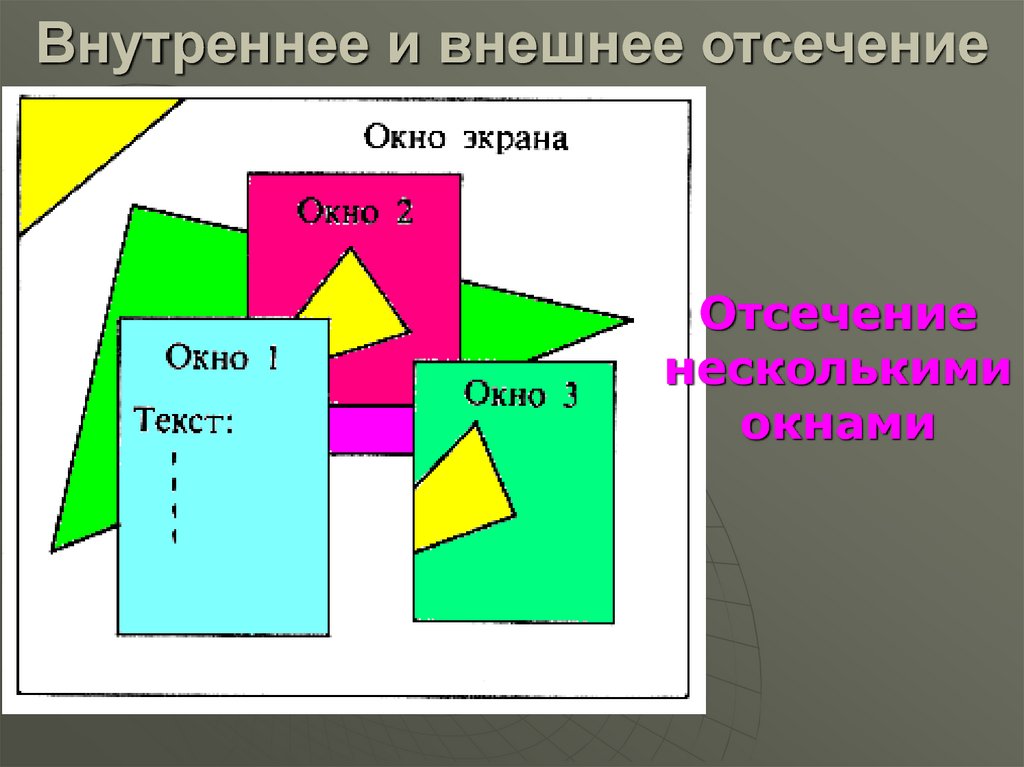
23. Внутреннее и внешнее отсечение
Отсечениенесколькими
окнами
24. Внутреннее и внешнее отсечение
Отсечениевогнутым
(невыпуклым)
полигональным
окном
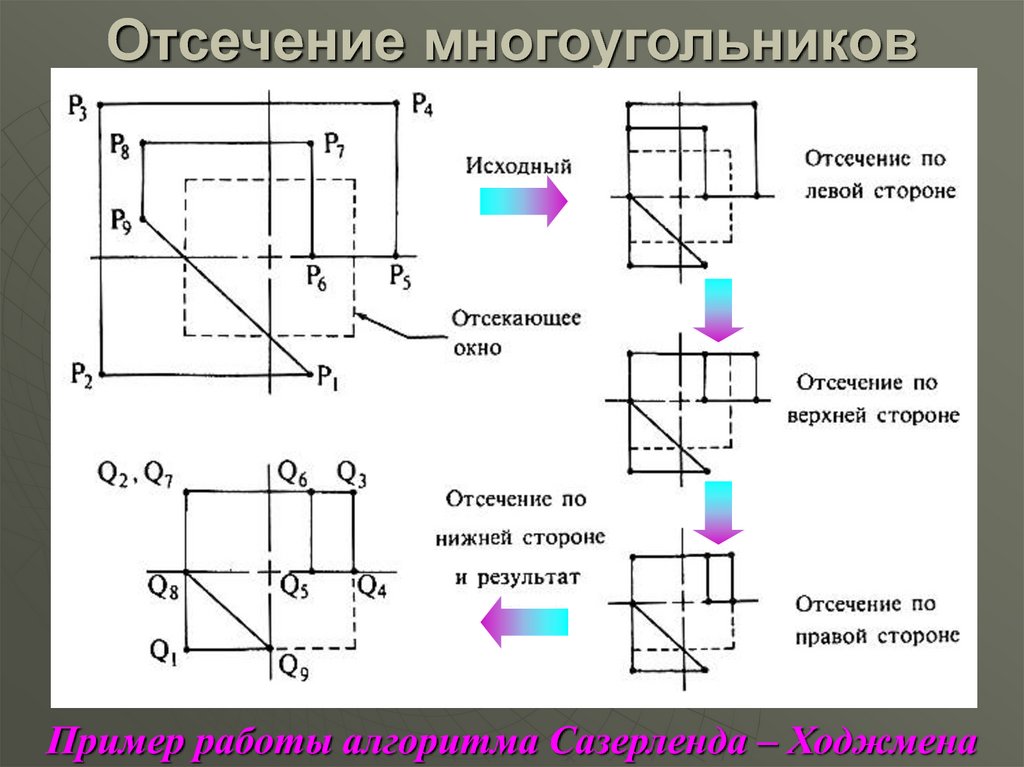
25. Отсечение многоугольников
Результат отсечения: открытый многоугольник26. Отсечение многоугольников
Результат отсечения: не связанные между собоймногоугольники
27. Отсечение многоугольников
Последовательное отсечение многоугольника28. Отсечение многоугольников
Взаимное расположение ребер и отсекающейплоскости
29. Отсечение многоугольников
Пример работы алгоритма Сазерленда – Ходжмена30.
Алгоритм Вейлера – Азертона:простой выпуклый отсекатель
Входы: I2 , I4 , I6 , I8
Выходы: I1 , I3 , I5 , I7
Результирующий внутренний многоугольник:
I2I3I4S3I5I6I7I8S6I1I2
Результирующий внешний многоугольник:
I1S7S1I2I1 (I3S2I4I3 , I5S4I6I5 , I7S5I8I7)
31.
Алгоритм Вейлера – Азертона:сложный обрабатываемый многоугольник
Входы: I1 , I3
Выходы: I2 , I4
Результирующий внутренние многоугольники:
I1S6I2C3I1 и I3I4C1I3
Результирующий внешний многоугольник:
I2S7S8S9I3C1I4S1S2S3S4S5I1C3I2
32.
Алгоритм Вейлера – Азертона:обрабатываемый многоугольник и отсекатель с «дырами»
Входы: I1 , I3 , I5
Выходы: I2 , I4 , I6
Результирующий внутренний многоугольник:
I1I2C6I3I4I5S8I6I1
Результирующий внешний многоугольник:
I2S1I3C6I2 (I4S2S3S4I1I6S5S6S7I5I4)
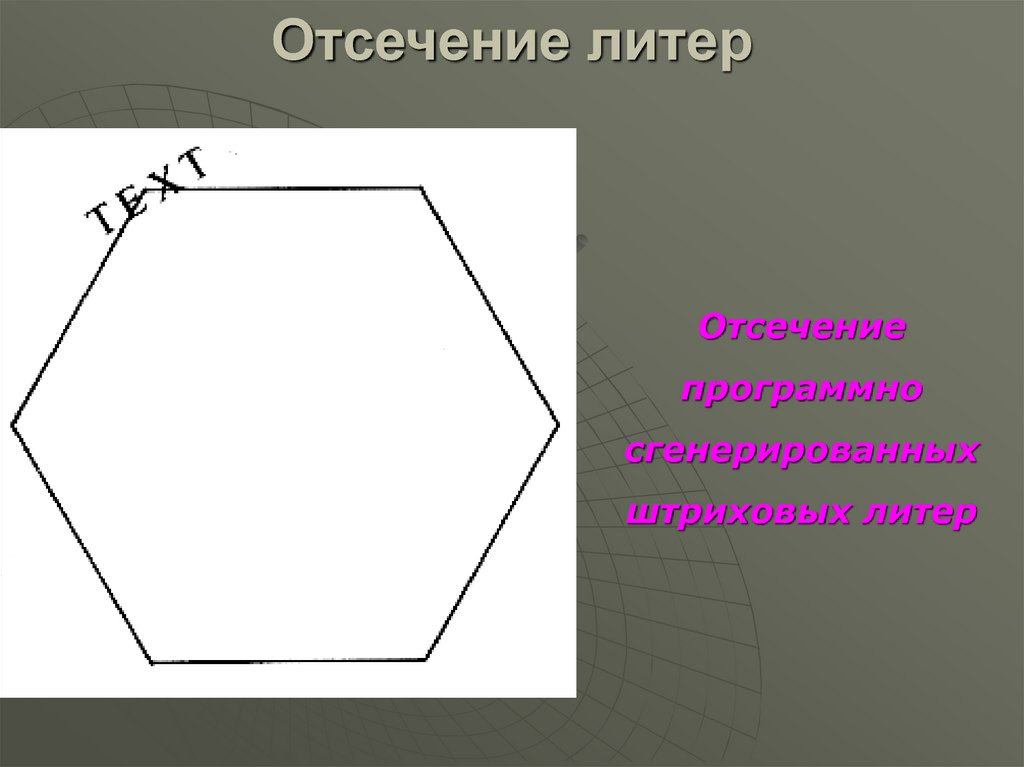
33. Отсечение литер
Отсечениепрограммно
сгенерированных
штриховых литер
34. Отсечение литер
Отсечение программно сгенерированныхточечных литер
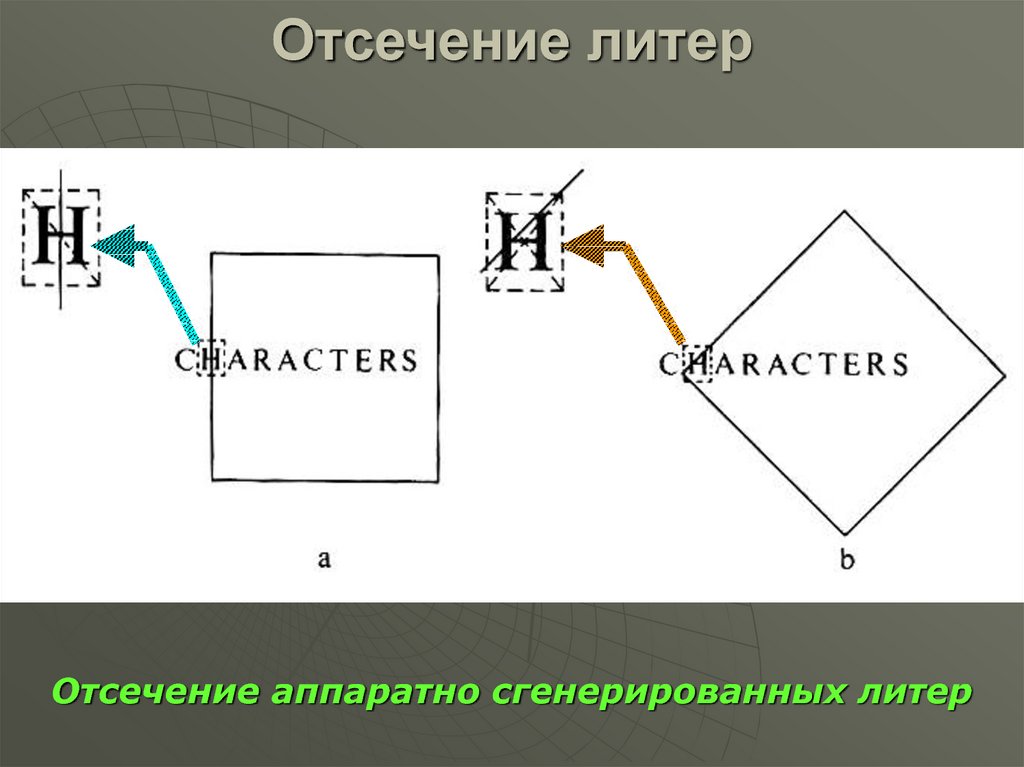
35. Отсечение литер
Отсечение аппаратно сгенерированных литер36. Закраска области, заданной цветом границы
Фигуры и контуры37. Закраска области, заданной цветом границы
Для данного контура –выход за границу на
следующих шагах работы
Для данного контура –
выход за границу
не получится
Контуры и границы закрашивания
38. Закраска области, заданной цветом границы
Пример работы волнового алгоритмазакрашивания
39. Закраска области, заданной цветом границы
Пример работы алгоритма закрашиваниялиниями
40. Закраска области, заданной цветом границы
Заполнение прямоугольника41. Закраска области, заданной цветом границы
Заполнение круга (эллипса)42. Закраска области, заданной цветом границы
Заполнение полигона43. Геометрические сплайны
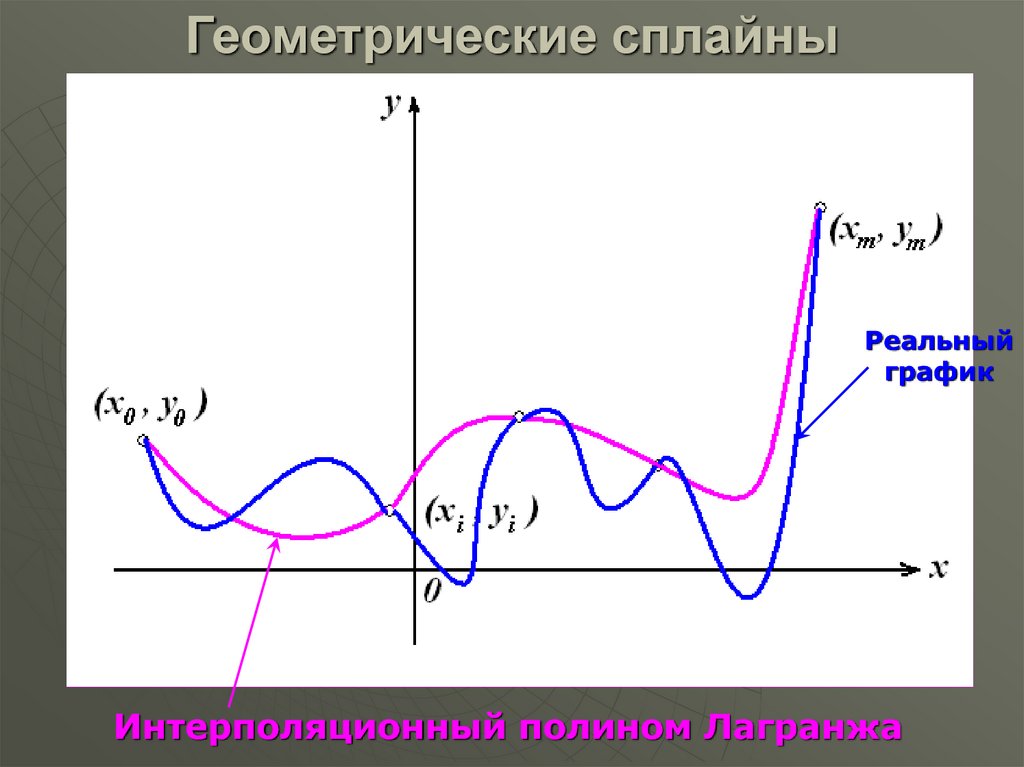
Набор точек44. Геометрические сплайны
Реальныйграфик
Интерполяционный полином Лагранжа
45. Геометрические сплайны
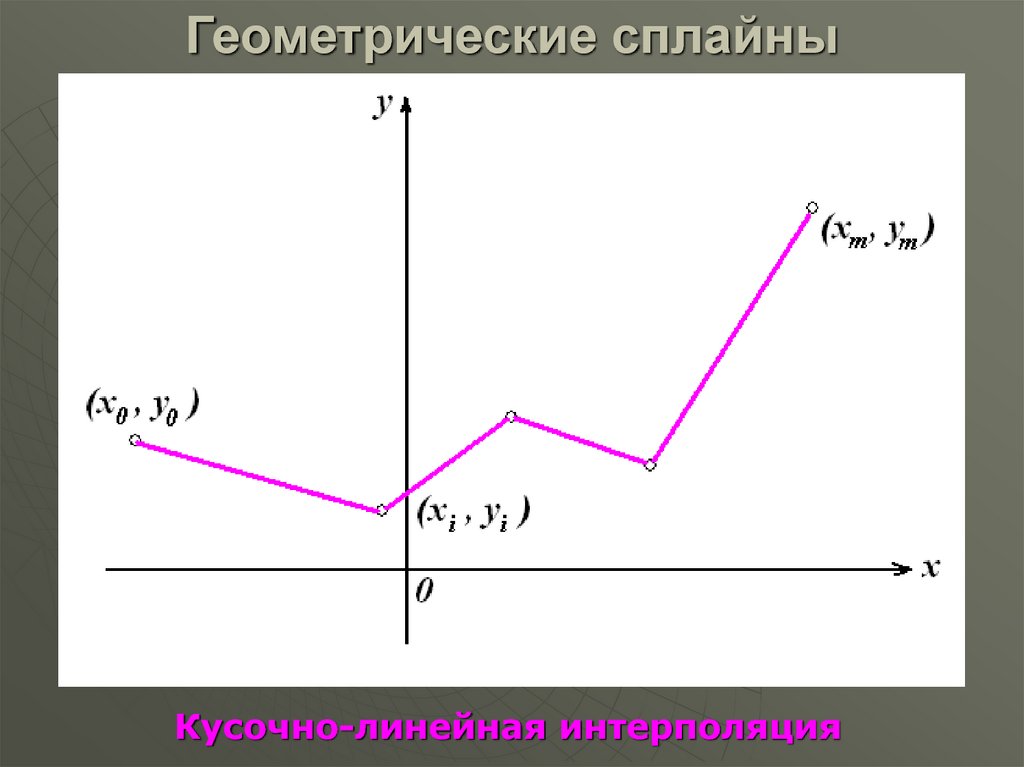
Кусочно-линейная интерполяция46. Геометрические сплайны
ЗакреплениеАссоциация с физическими сплайнами
47. Геометрические сплайны
mr (t ) C m t
i 0
i
i
(1 t ) V
Кривая Безье
m i
i
48. Геометрические сплайны
r (t ) (1 t )V 0 t V 1 , 0 t 1Кривая Безье при m=1
49. Геометрические сплайны
r (t ) (1 t ) V 0 2t (1 t )V 1 t2
2
V
Кривая Безье при m=2
,
0
t
1
2
50. Геометрические сплайны
r (t ) (1 t ) V 0 3t (1 t )3
2
V
3t (1 t )V
1
tV
3
2
2
Кривая Безье при m=3
3
, 0 t 1
51. Геометрические сплайны
«Геометрический» подход к построению кривойБезье
52. Геометрические сплайны
3t 3 6t 2 43t 3 3t 2 3t 1
(1 t )
r (t )
V
V
V
0
1
6
6
6
3
2
t
6
3
V
3
, 0 t 1
Элементарная кубическая В-сплайновая кривая
53. Геометрические сплайны
3r (t )
w n (t )V
i
i 0
3
i
i
w n (t )
i 0
i
, 0 t 1
i
3t 6t 4
(1 t )
Здесь n0 (t )
, n1 (t )
,
6
6
3
3
2
3t 3t 3t 1
t
n2 (t )
, n3 (t )
,
6
6
3
3
а wi веса ( параметры формы) :
2
3
w
i 0
i
0.
Рациональная кубическая В-сплайновая кривая
54. Геометрические сплайны
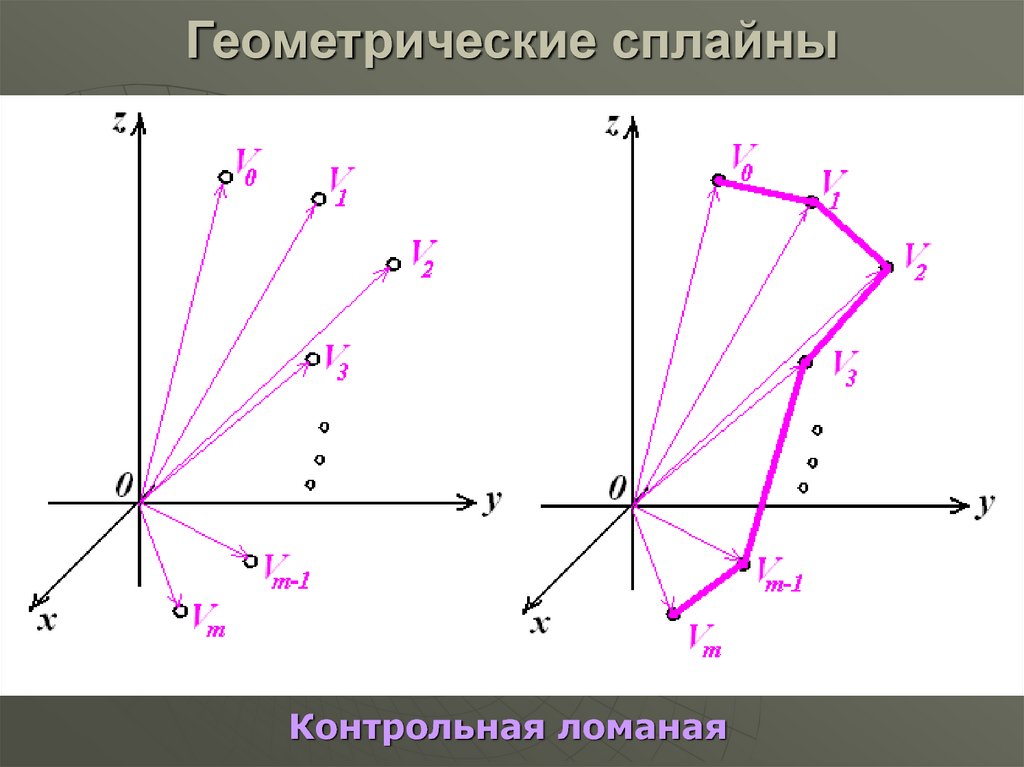
Контрольная ломаная55. Геометрические сплайны
Условия геометрической непрерывности :r2 (0) r1 (1); r2 (0) 1r1 (1); r2 (0) 21r1 ( 1) 2 r1 (1) ,
где 1 0 , 2 0
ri (t )
1
b (t )V
j 2
i j
j
, 0 t 1
3
Здесь b j (t ) ckj ( 1 , 2 )t k , j 2, 1, 0, 1
k 0
Бета-сплайны
56. Геометрические сплайны
11
b j (0)Vi 1 j b j (1)Vi j ,
j 2
j 2
1
1
b j (0)Vi 1 j 1 b j (1)Vi j ,
j 2
j 2
1
1
1
2
b j (0)Vi 1 j 1 b j (1)Vi j 2 b j (1)Vi j
j 2
j 2
j 2
Бета-сплайны (условия геометрической непрерывности)
57. Геометрические сплайны
2 4 1 4 1 2 2 02
3
1
определитель системы
b 2 (t )
b 1 (t )
2 31
1
(1 t ) 3 ;
[2 31t (t 2 3t 3) 2 21 (t 3 3t 2 2)
2 1 (t 3 3t 2) 2 (2t 3 3t 2 1)];
b0 (t )
1
[2 21t 2 ( t 3) 2 1t ( t 2 3)
2t 2 ( 2t 3) 2( t 3 1)];
b1 (t )
2t 3
Бета-сплайны (коэффициенты bj(t))
58. Геометрические сплайны
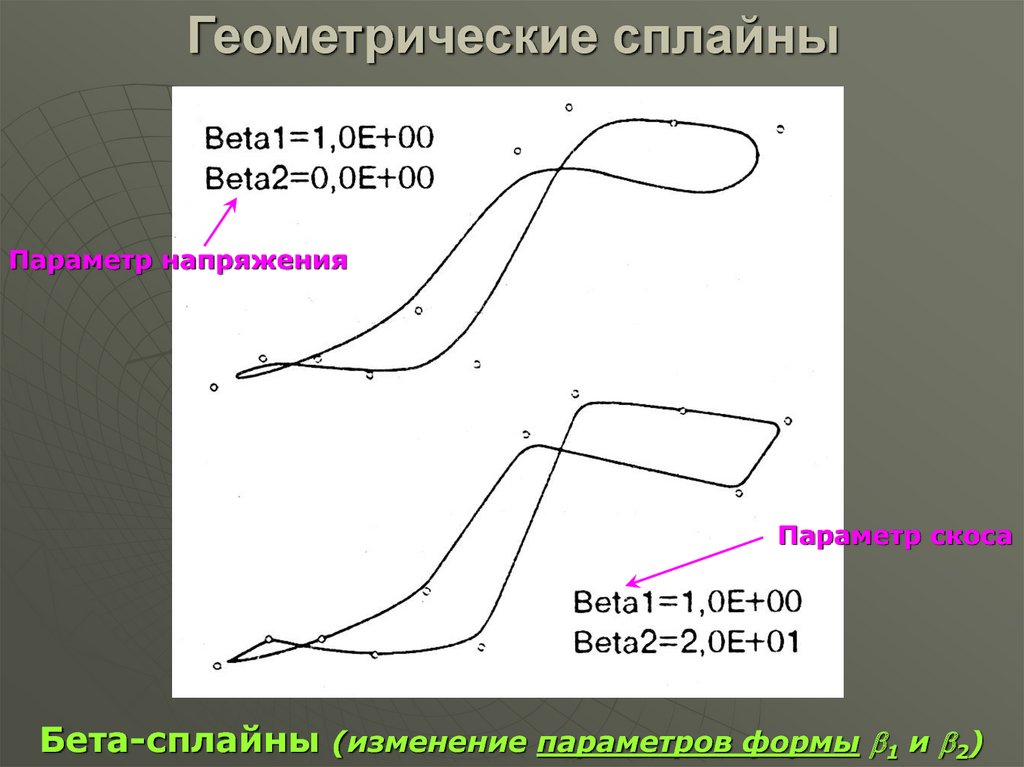
Параметр напряженияПараметр скоса
Бета-сплайны (изменение параметров формы 1 и 2)















































 Информатика
Информатика








