Похожие презентации:
Квантование. Дискретная случайная величина
1. Квантование
2. Квантование
Дискретная случайная величина –случайная величина, которая может
принимать конечное число значений.
Непрерывная случайная величина –
случайная величина, которая может
принимать бесконечное число значений.
Квантование – замена непрерывной
случайной величины дискретной.
3. Виды сообщений
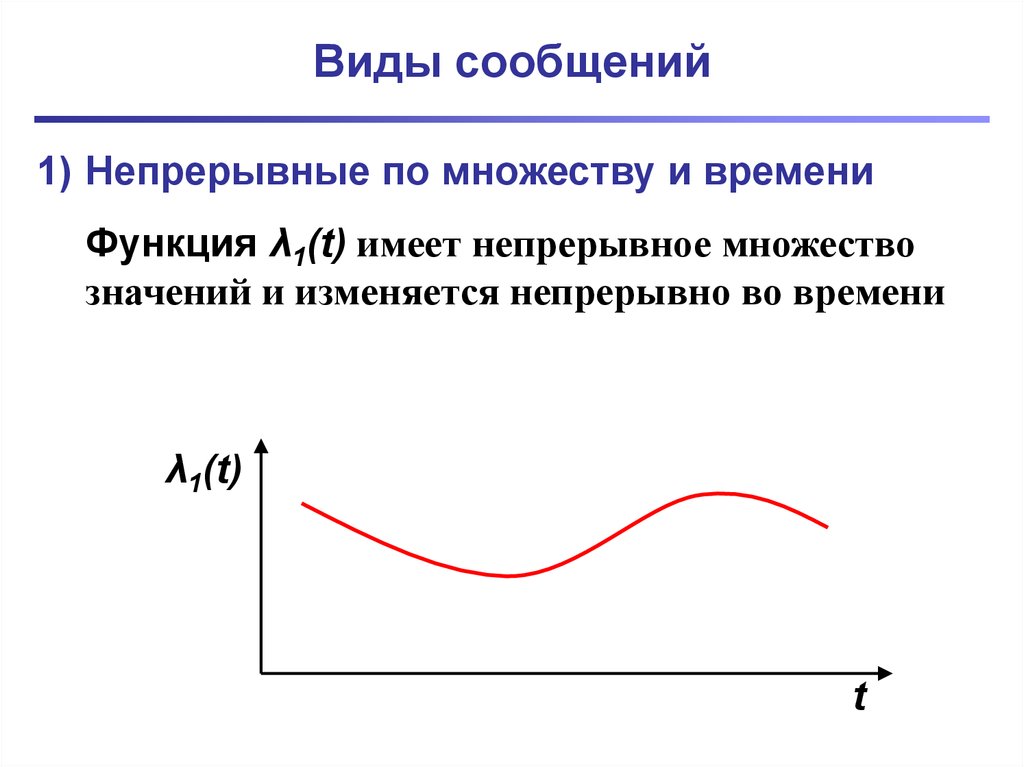
1) Непрерывные по множеству и времениФункция λ1(t) имеет непрерывное множество
значений и изменяется непрерывно во времени
λ1(t)
t
4. Виды сообщений
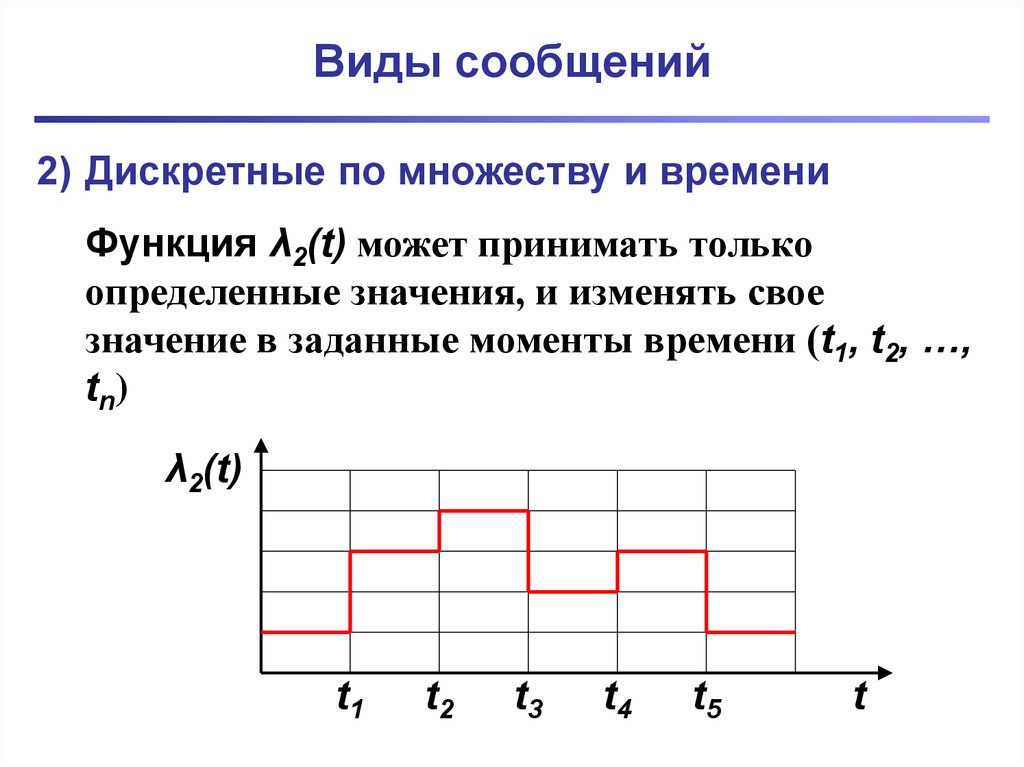
2) Дискретные по множеству и времениФункция λ2(t) может принимать только
определенные значения, и изменять свое
значение в заданные моменты времени (t1, t2, …,
tn)
λ2(t)
t1
t2
t3
t4
t5
t
5. Виды сообщений
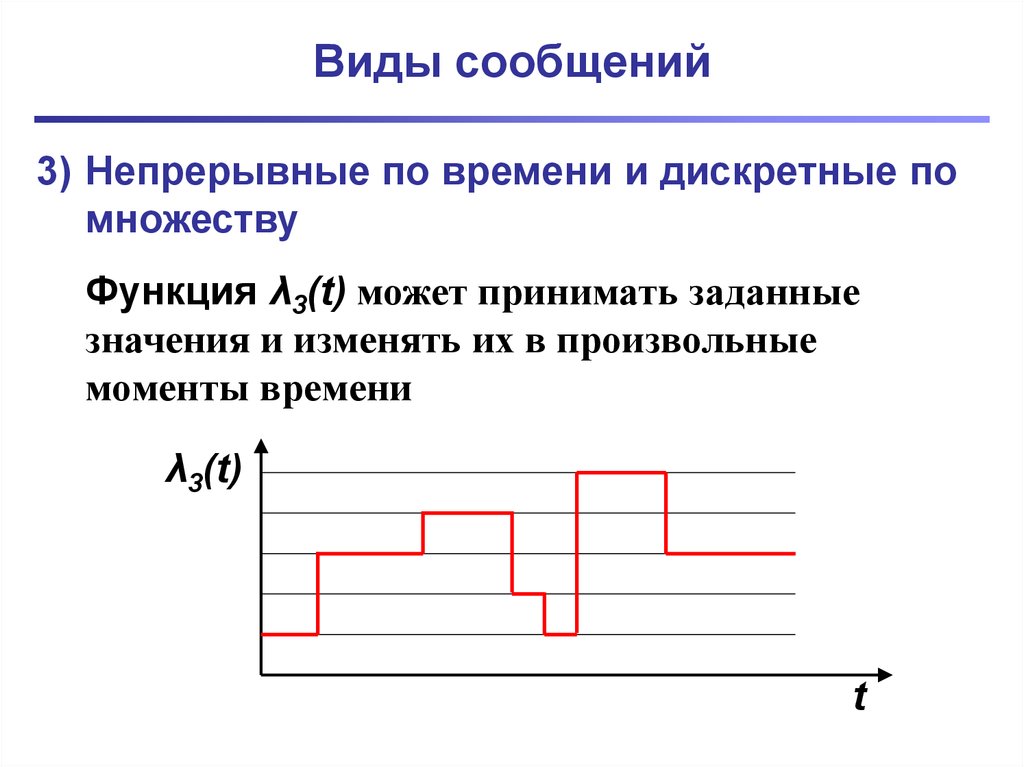
3) Непрерывные по времени и дискретные помножеству
Функция λ3(t) может принимать заданные
значения и изменять их в произвольные
моменты времени
λ3(t)
t
6. Виды сообщений
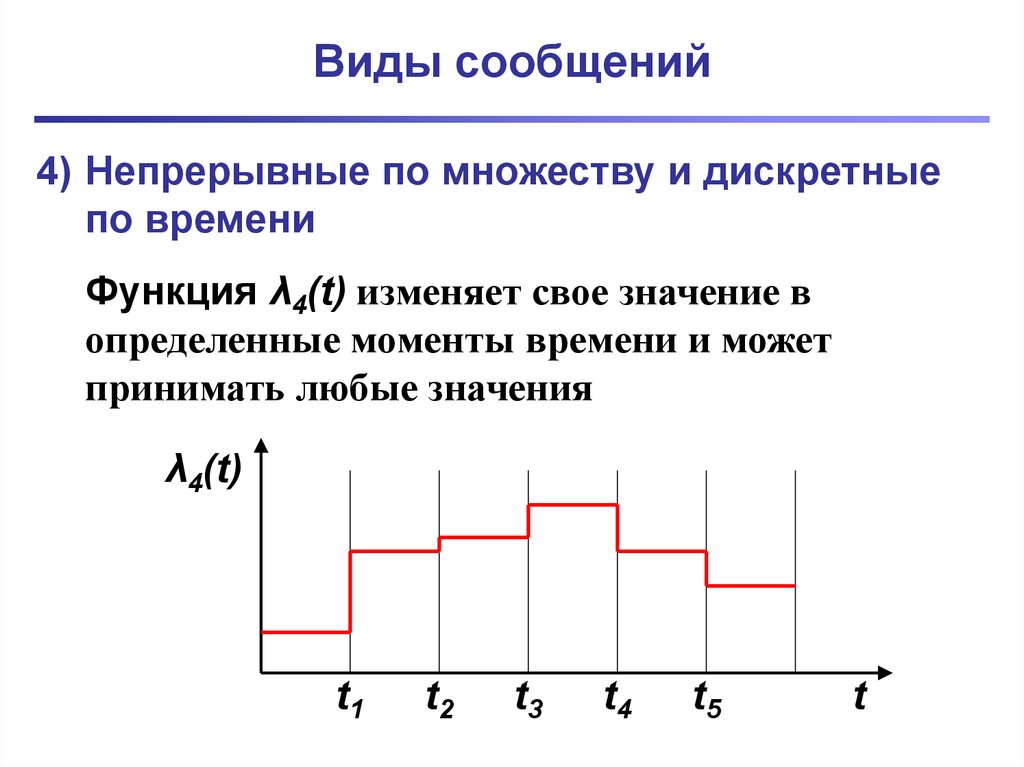
4) Непрерывные по множеству и дискретныепо времени
Функция λ4(t) изменяет свое значение в
определенные моменты времени и может
принимать любые значения
λ4(t)
t1
t2
t3
t4
t5
t
7. Квантование по уровню
Квантование по уровню (квантование попараметру) – процесс замены непрерывной
функции ее отдельными значениями,
отстоящими друг от друга на конечный
интервал.
Шаг квантования –интервал между двумя
дискретными значениями уровней.
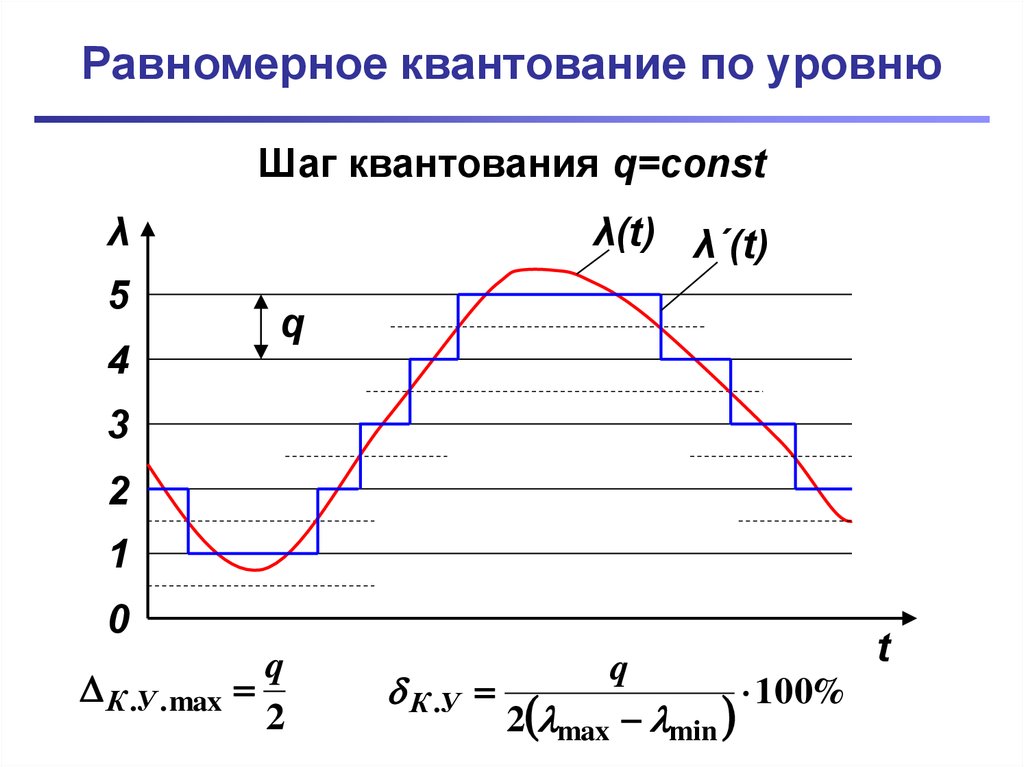
8. Равномерное квантование по уровню
Шаг квантования q=constλ
5
4
λ(t) λ´(t)
q
3
2
1
0
К .У . max
q
2
К .У
q
100%
2 max min
t
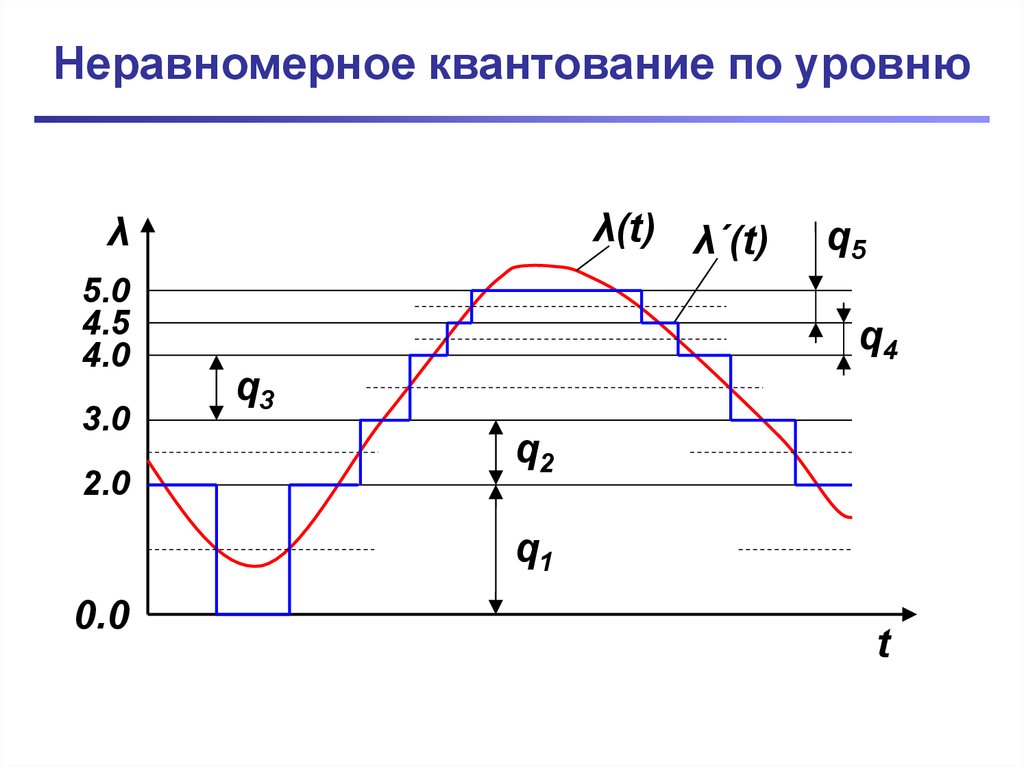
9. Неравномерное квантование по уровню
λ(t) λ´(t)λ
5.0
4.5
4.0
3.0
2.0
q5
q4
q3
q2
q1
0.0
t
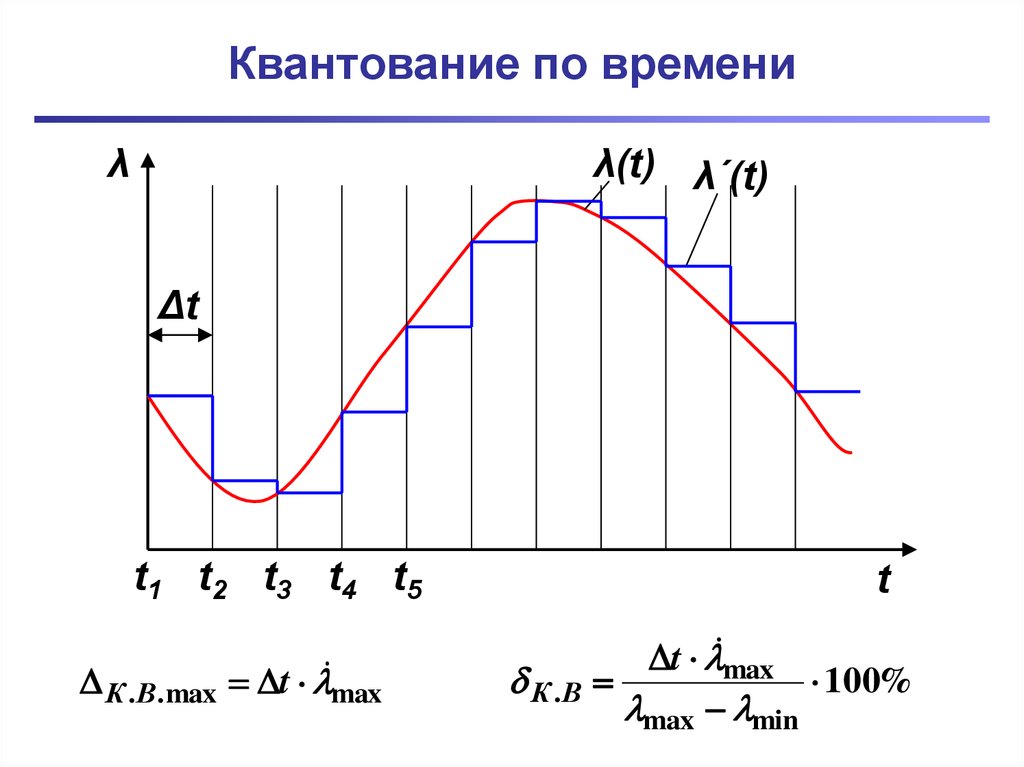
10. Квантование по времени
Квантование по времени (дискретизация) –процесс замены непрерывной функции ее
отдельными значениями в определенные
моменты времени.
11. Квантование по времени
λλ(t) λ´(t)
Δt
t1 t2 t3 t4 t5
К . В. max t max
t
К .В
t max
100%
max min
12. Квантование по уровню и времени
Квантование по уровню и времени –процесс замены непрерывной функции ее
отдельными значениями, отстоящими друг
от друга на конечный интервал, в
определенные моменты времени.
К.У.В
2
К .У
2
К.В





 Информатика
Информатика








