Векторлар өрісінің циркуляциясы, роторы

1. ЭЛЕКТР ЖӘНЕ МАГНЕТИЗМ, АТОМДЫҚ ФИЗИКАНЫҢ АРНАЙЫ ТАРАУЛАРЫ

2. Векторлар өрісінің циркуляциясы, роторы

Дивергенция –өрістің жергілікті сипаттамасы.
Li
Si 0 S
i
lim
шегі Si элементар беті ұмтылатын нүктедегі өрістің құйынының
қуатын береді.
Кез-келген S беті керіп тұрған тұйық Г контуры бойымен алынған
векторлар өрісінің LГ циркуляциясы S бетінің Si бөліктері тірелетін
Элементар контурлар бойынша алынған
тең.
N
L
Lі
циркуляцияларының қосындысына
dl
i 1 i
i
dli
N
L Li
i 1
Векторлар өрісінің роторының шамасы, басқаша айтқанда, векторлар өрісінің құйынының қуаты
ауданы нөлге ұмтылатын өте кішкене бет керіп тұрған тұйық контур бойымен алынған
циркуляция.
Ротор- өрістің нүктесінің қасиетін сипаттайтын вектор. Ол векторлар өрісінің сәйкесті
циркуляциясының ең үлкен мәніне сәйкесті контуры орналасқан жазықтыққа орналасқан
жазықтыққа перпендикуляр.

3. Стокс теоремасы

Li
rot n
S i
Si
dl ( rot )
S
n
dS

4. Электромагетизм заңдары

1. Электромагнетизмнің бірінші заңы электр өрісінің ағынын былай анықтайды:
кернеулігінің
электр өрісінің Е
тұйық бет ішіндегі заряд
0
кез-келген тұйық бет арқылы
өтетін ағыны
Егер тұйық беттің ішінде заряд жоқ болса, онда оның сыртында қанша заряд болса да, ол
бет арқылы өтетін электр өрісінің ағыны нөлге тең.
2. Электромагнетизмнің екінші заңы электр өрісінің циркуляциясы мен магнит өрісі
индукция векторы арасындағы байланысты тағайындайды.
векторының
Е
S тұйық беті арқылы
Г контуры
ағып өтетін
бойынша
алынған
векторының ағыны
циркуляциясы t B

5. Электромагетизм заңдары

3. Электромагниттік өрістің заңдары толық болуы үшін В магнит индукция векторының
ағыны мен циркуляциясы үшін заң
Магнит индукция векторының
т
B
0
кез-келген
тұйық бет арқылы
өтетін ағыны
Егер тұйық беттің ішінде заряд жоқ болса, онда оның сыртында қанша заряд болса да, ол
бет арқылы өтетін электр өрісінің ағыны нөлге тең.
Кез-келген S беті тіреліп
беті арқылы өтетін
тұрған тұйық Г контуры Sбеті арқылы
S электр тогы
алынған
өтетін
Bбойынша
векторының ағыны
векторының
0
циркуляциясы
t E
j B
F q E
Осы заңдарға
n
теңдеулер жүйесі толық алынады.
1
теңдеуін қоссақ, электродинамиканың

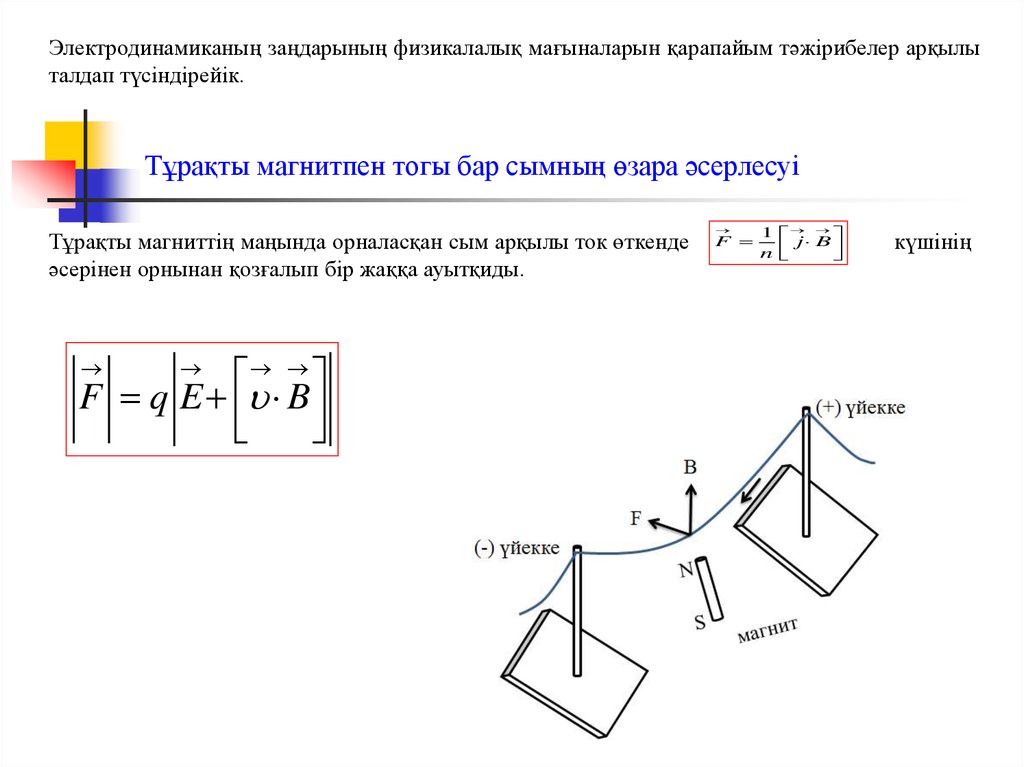
6. Тұрақты магнитпен тогы бар сымның өзара әсерлесуі

Электродинамиканың заңдарының физикалалық мағыналарын қарапайым тәжірибелер арқылы
талдап түсіндірейік.
Тұрақты магнитпен тогы бар сымның өзара әсерлесуі
Тұрақты магниттің маңында орналасқан сым арқылы ток өткенде
әсерінен орнынан қозғалып бір жаққа ауытқиды.
F q E B
F
1
j B
n
күшінің

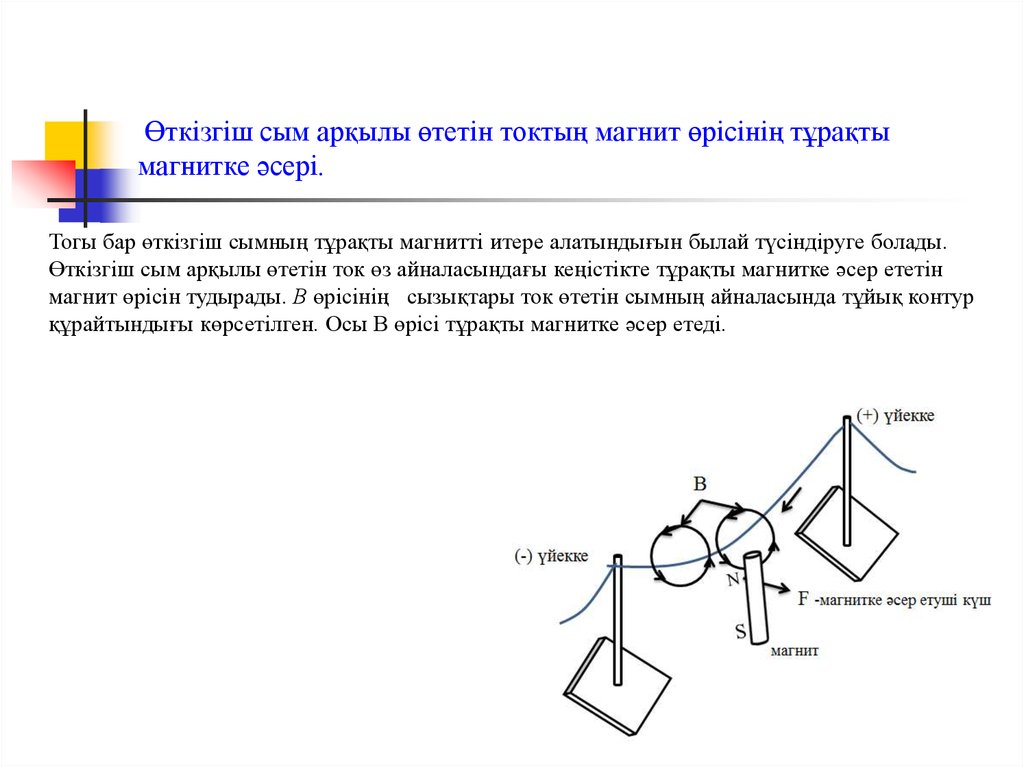
7. Өткізгіш сым арқылы өтетін токтың магнит өрісінің тұрақты магнитке әсері.

Тогы бар өткізгіш сымның тұрақты магнитті итере алатындығын былай түсіндіруге болады.
Өткізгіш сым арқылы өтетін ток өз айналасындағы кеңістікте тұрақты магнитке әсер ететін
магнит өрісін тудырады. В өрісінің сызықтары ток өтетін сымның айналасында тұйық контур
құрайтындығы көрсетілген. Осы В өрісі тұрақты магнитке әсер етеді.

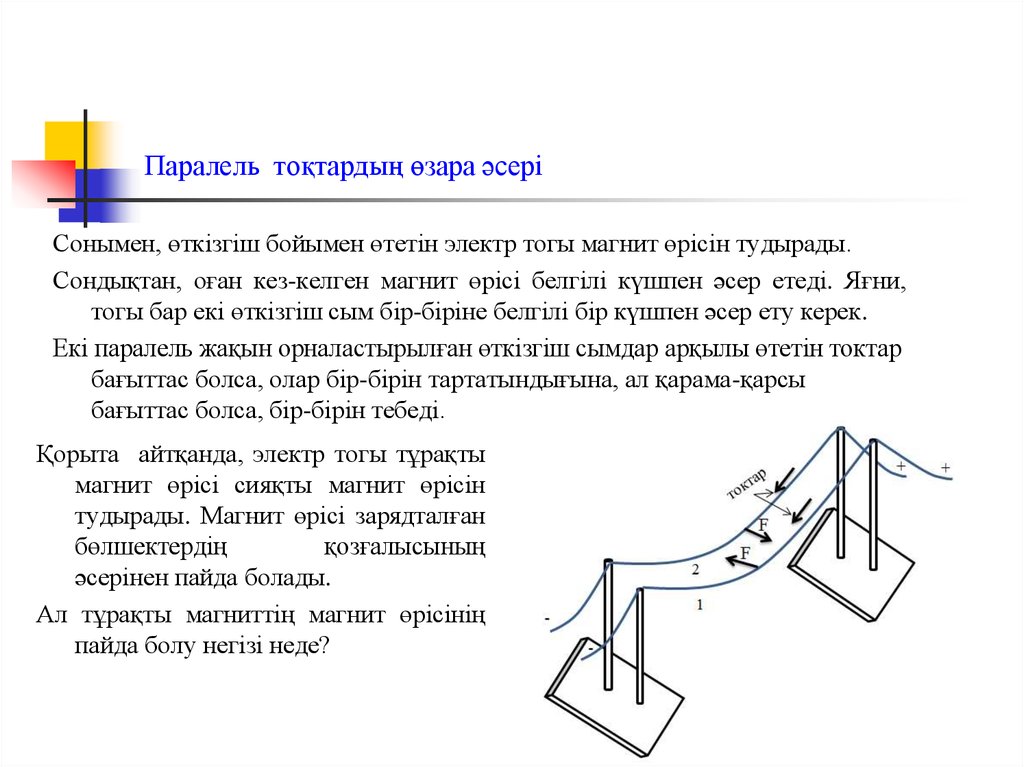
8. Паралель тоқтардың өзара әсері

Сонымен, өткізгіш бойымен өтетін электр тогы магнит өрісін тудырады.
Сондықтан, оған кез-келген магнит өрісі белгілі күшпен әсер етеді. Яғни,
тогы бар екі өткізгіш сым бір-біріне белгілі бір күшпен әсер ету керек.
Екі паралель жақын орналастырылған өткізгіш сымдар арқылы өтетін токтар
бағыттас болса, олар бір-бірін тартатындығына, ал қарама-қарсы
бағыттас болса, бір-бірін тебеді.
Қорыта айтқанда, электр тогы тұрақты
магнит өрісі сияқты магнит өрісін
тудырады. Магнит өрісі зарядталған
бөлшектердің
қозғалысының
әсерінен пайда болады.
Ал тұрақты магниттің магнит өрісінің
пайда болу негізі неде?

9.

Электр тізбегінің жазық конденсатор орналасқан бөлігін қарастырайық.
Тогы бар өткізгіш сымның айналасында орналасқан С тұйық контурына
тірелетін S1 беті тогы бар өткізгіш сымды қиып өтетін болсын.

10. Қорытынды

- Кез-келген тұйық бет арқылы өтетін электростатикалық өрістің ағыны оның ішінде
орналасқан зарядтардың шамасымен (алгебралық қосындысымен анықталады), оның
пішініне, өлшеміне тәуелді болмайды.
- Электростатикалық өрістің көзі - заряд.
Гаусс
теоремасы,
біріншіден,
зарядтардың
өзара
әсерлері
олардың
арақашықтықтарының квадратына кері пропорционал екендігіне, екіншіден,
тәуелсіздік принципіне негізделген. Кулон заңы мен Гаусс теоремасы өзара балама.
-Кулон заңының көмегімен берілген тыныштықтағы зарядтар жүйесінің электр өрісін
анықтауға болады. Ал, Гаусс теоремасы арқылы өріс нүктелеріндегі кернеуліктерді біле
отырып, зарядтың шамасын анықтауға болады.

11. Де Бройль толқындарын ықтималдылық мағыналау

Де Бройль толқындарының берілген нүктедегі амплитудасының
модулінің квадраты бөлшектің осы нүктеде табылу
ықтималдылығының өлшемі болып табылады.
1926 ж. М. Борн
заң бойынша ықтималдылықтың өзі
( xтолқындық
, y, z , t )
емес, ықтималдылықтың амплитудасы деп аталатын шама өзгереді
деп ұйғарды. Осы шама
функциясы арқылы
белгіліенеді, ол толқындық функция деп аталады.
dw dV dxdydz
2
2
*
2
w
dV 1
2
dw
dV
2
*
dV 1

12. Анықталмағандық қатынас

1927 ж. неміс физигі В. Гейзерберг микродүние объектісін
бір мезгілде алдын-ала беогілі дәлдікпен анықталған
координат пен импульспен сипаттау мүмкін емес деген.
x px , y p y , z pz
x 0 ; px
x ; px 0
2
2
; px p sin
sin
p
x px
x sin
x x
2
m 10 кг х 10 м х 6,62 10 14 м / с
х 7, 27 106 м / с
х 10 10 м
12
Е t
8
2,3 106 м / с

13. Шредингер теңдеуі. Кванттық теориядағы күй түсінігі және оны толқындық функция арқылы бейнелеу. Суперпозиция принципі.

Шредингер теңдеуі. Стационар күйлер. Квантталу.
Операторлар жайында.
Классикалық физикада бөлшектің күйі деген ұғымның
анықтамасы былай беріледі. Егер берілген уақыт мезетінде
бөлшектің x, y, z координаттары және жылдамдығының x , y,
z құраушылары белгілі болса, онда (осы шамалар толығымен)
бөлшек күйі анықталған делінеді. Яғни классикалық бөлшек
күйі берілген уақыт мезетіндегі бөлшектің радиус-векторы
және жылдамдығымен анықталады.
, m
c2
2
,
p
m
c
.
2
c
c
Кванттық механикада бөлшек күйінің берілуі классикалық
механикаға қарағанда өзгеше болуға тиіс. Микробөлшектер
үшін анықталмағандық қатынастарының болуынан бөлшектің
күйін координаттар мен импульс арқылы классикалық
анықтау жалпы алғанда мағынасын жояды. Корпускулалықтолқындық дуализмге сәйкес кванттық теорияда бөлшектің
күйі (r, t) функциясымен беріледі, ол комплекс шама және
формальды түрде толқындық қасиеттерге

14.

Барлық кванттық ықтималдықтар ішінен бөлшектердің
координаттарының үлестірілуін бейнелейтін ықтималдықты
қарастырайық. Бір өлшемді қозғалыс үшін бөлшектің t уақыт
мезетінде х және х+dx нүктелері аралығында болу ықтималдығы
(х,t) 2dx-қа тең, мұндағы (х,t) 2= (х,t) (х,t) – толқындық
функция модулінің квадраты, – комплекс түйіндес функция.
w( x ,t ) w( x ,t )
(5.1)
шамасы ықтималдық тығыздығы, немесе бөлшек координаттарының
үлестірілу тығыздығы.
Ықтималдық тығыздығы нормалау шартына бағынады:
w( x ,t )dx
( x ,t ) dx 1
2
(5.2)
бұл шарт бөлшектің х осінде болуы ақиқат екендігін өрнектейді.
(х,t) толқындық функция көмегімен координаттың орташа мәні
былай анықталады:
x( t )
xw( x ,t )dx
x ( x ,t ) dx
2

15.

Толқындық функция, оның физикалық мағынасынан келіп шығатын
белгілі шарттарды қанағаттандыруға тиіс. Ол координат пен уақыттың
үздіксіз функциясы болуы тиіс. Толқындық функция бір мәнді және
шектелген болуға тиіс. Осы математикалық талаптар жиынтығы үлгі
шарттар деп аталады және нақты физикалық шарттарға сәйкес келеді:
бөлшектің берілген орында болу ықтималдығы бір нүктеден келесі
нүктеге біртіндеп өзгеруге (үздіксіздік), берілген нүкте үшін нақты (бір
мәнділік), шектелген болуға тиіс.
Егер бөлшектің кеңістіктің көлемі V белгілі аймағында ғана
қозғалатыны белгілі болса, онда осы аймақта оның табылу
ықтималдығы 1-ге тең болады.
Кванттық теорияда негізгі постулаттардың бір ретінде псифункцияның суперпозиция принципі қабылданылады. Егер
қандайда бір жүйеде 1 және 2 күйлері мүмкін болса, онда ол
үшін мынадай күй де мүмкін болады:
a1 1 a2 2 ,
мұндағы a1 және a2 – қайсыбір тұрақты коэффициенттер.
Осылай -ді тауып, бұдан кейін жүйенің осы күйде болу
ықтималдығының тығыздығын да анықтауға болады.
(5.4)

16. Шредингер теңдеуі

2
i
U
t
2m
(5.5)
мұндағы m – бөлшек массасы, і – жорамал бірлік (), U – бөл-шектің
потенциалдық энергиясы, – Лаплас операторы. (5.5) теңдеуінен
толқындық функцияның түрін U функция, яғни түптеп келгенде
бөлшекке әсер ететін күштердің сипаты анықтайтындығы шығады.
(5.5) теңдеуін Шредингердің жалпы теңдеуі дейді.
Стационарлық күйлер. Кванттық теорияда ерекше рольді
стационарлық күйлер атқарады, бұларда барлық бақыланатын
физикалық шамалар уақыт өткенде өзгермейді.
-функцияның өзі негізінде бақыланбайды. Стационарлық күйлерде
ол мына түрге келеді
i t
( r ,t ) ( r )e , E /
мұндағы (r) – функция уақытқа тәуелді емес.
(5.6)

17. Cтационарлық күйлер үшін Шредингер теңдеуі

Стационарлық күйлердегі (r)-функцияны табу үшін (5.6) өрнекті
(5.5) теңдеуіне қоямыз,
2 сонда мына теңдеу шығады:
(5.7)
2m
U E
Бұл теңдеу стационарлық күйлер үшін Шредингер теңдеуі
деп аталады.
2m
2 E U ( r ) 0
(5.8)
Квантталу. Бордың теориясында квантталу жасанды түрде
ендірілген болса, Шредингер теориясында ол өзінен-өзі шығады.
Сонда (5.8) теңдеуінің шешімдері ішінен физикалық мағынаға
табиғи немесе үлгі (стандарт) шарттарды
қанағаттандыратын шешімдері ғана ие болатынын ескеру
жеткілікті болады. Осы шарттарды қанағаттандыратын
шешімдер Е энергияның кейбір мәндерінде ғана мүмкін болады
екен. Бұларды меншікті мәндер деп, ал энергияның осы
мәндерінде (5.8) теңдеуінің шешімдері болып табылатын (r)функциялары Е-нің меншікті мәндеріне сай меншікті
функциялар деп аталады.

18. Физикалық шамалардың операторлары жайындағы түсінік

Оператор.
1926 ж. М.Борн,
Н.Винер әрбір классикалық
физикалық шамаға белгілі қасиеттерге ие, қайсыбір оператор
салыстырылады деген идея ұсынды. Оператор-шартты белгі,
немесе ереже; оны қолдану арқылы бір функциядан басқа
функцияны алуға болады. Физикада операторлар әдетте үстіне
таңбасын қойып белгіленеді:
L x x .
Оператор қасиеттері. Операторлардың қосындысы да
оператор болады.
( L1 L2 ) L1 L2 L
À
B
A B .

19. Кванттық механиканың негізгі постулаттары.

1-постулат.
Әрбір динамикалық айнымалыға, әрбір физикалық
шамаға (координат, импульс, энергия және т.б.) белгілі эрмиттік
оператор сәйкес келеді.
операторлар” енгізілуге
Осы постулатқа сәйкес “физикалық
тиіс:
ð
r
H
координат операторы,
импульс операторы,
энергия
операторы және т.б.
2-постулат. операторымен кескінделетін қайсыбір
динами-калық айнымалының сан мәнін өлшегенде,
операторының меншікті мәні болып табылатын 1, 2,
... сандарының бірі белгілі ықтималдықпен алынады.
3-постулат. толқындық функция бейнелейтін кезкелген күйде L динамикалық айнымалы шамасының
математикалық күтуі, толқындық функция
нормаланған жағдайда, мына формуламен
өрнектеледі:
L L dV

20. Физикалық шамалардың операторлары.

Координат және импульс
проекциясының операторлары
2
кванттық механиканың
болып
x xнегізгі
( x ) операторлары
dx
табылады.
P x i
Импульс проекциясының операторы ретінде мына оператор
x
алынады:
T
2
2
2
2m
2
2
Кинетикалық энергия
операторы
2
2
p
2
ГамильтонHоператоры
U(гамильтониан)
(r )
U( r )
2m
2m