Похожие презентации:
Жарықтың изотропты ортада таралуы
1. Жарықтың изотропты ортада таралуы
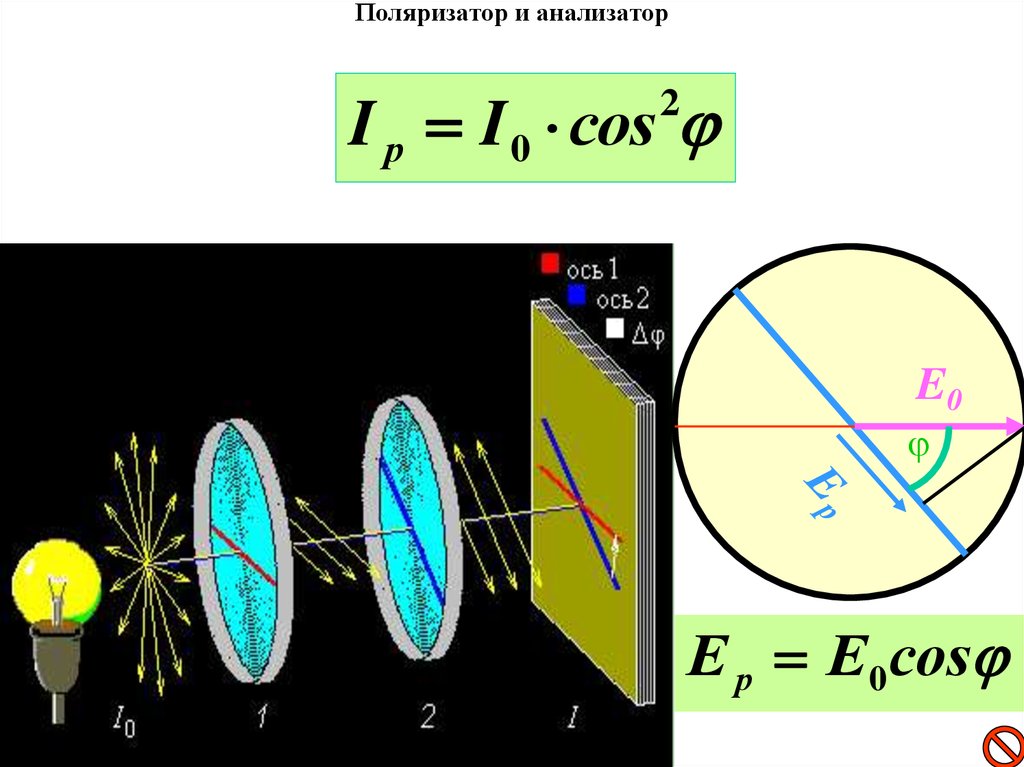
2. Поляризатор и анализатор
I р I 0 сos j2
E0
j
Е р Е 0 сosj
3. Жарықтың электромагниттік табиғатына шекаралық шарттар
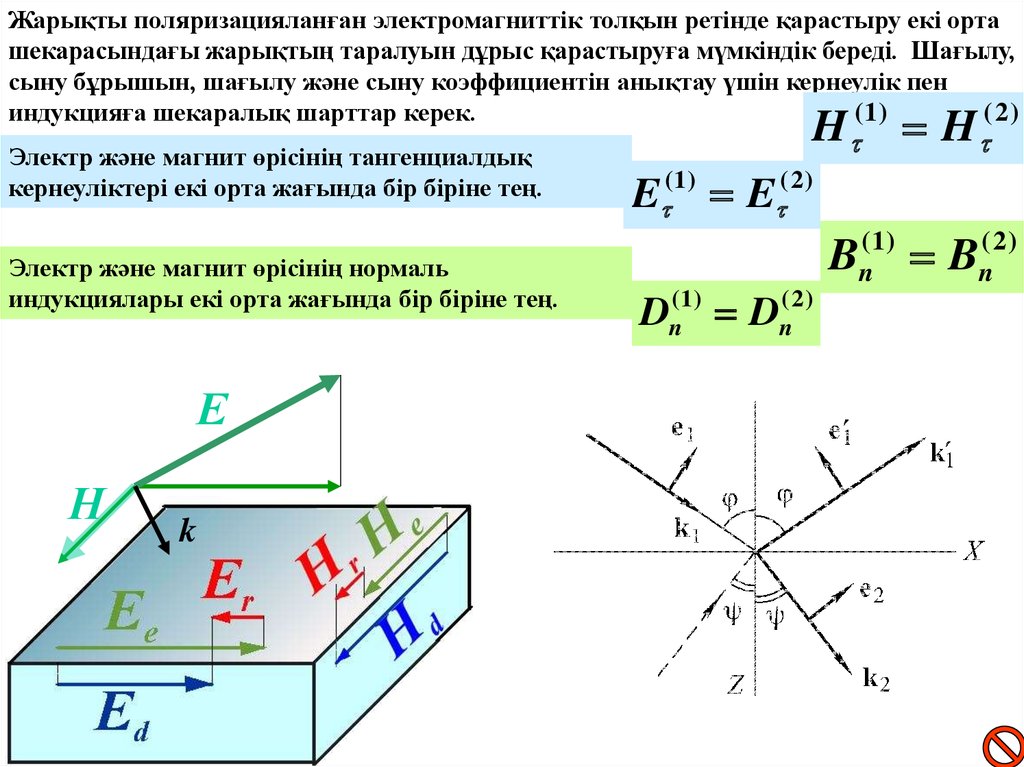
Жарықты поляризацияланған электромагниттік толқын ретінде қарастыру екі орташекарасындағы жарықтың таралуын дұрыс қарастыруға мүмкіндік береді. Шағылу,
сыну бұрышын, шағылу және сыну коэффициентін анықтау үшін кернеулік пен
индукцияға шекаралық шарттар керек.
(1)
( 2)
Электр және магнит өрісінің тангенциалдық
кернеуліктері екі орта жағында бір біріне тең.
Электр және магнит өрісінің нормаль
индукциялары екі орта жағында бір біріне тең.
Е
Н
k
H H
E (1) E ( 2 )
Dn(1) Dn( 2 )
Bn(1) Bn( 2 )
4. Изотропный диэлектрик
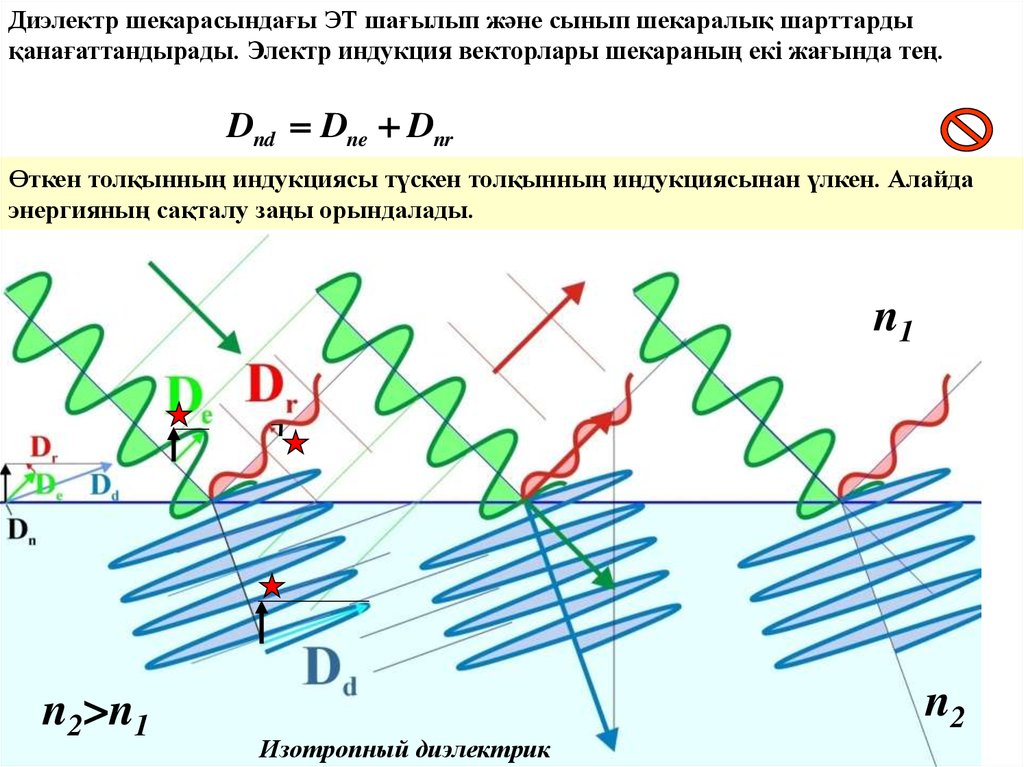
Диэлектр шекарасындағы ЭТ шағылып және сынып шекаралық шарттардықанағаттандырады. Электр индукция векторлары шекараның екі жағында тең.
Dnd Dne Dnr
Өткен толқынның индукциясы түскен толқынның индукциясынан үлкен. Алайда
энергияның сақталу заңы орындалады.
n1
n2>n1
n2
Изотропный диэлектрик
5.
Шекаралық шарттар жазық толқын фронтының әр нүктесінде және барлықуақытта бірдей болу үшін электрлік индукцияның үш құраушысы таралады: Dne ,
Dnr , D nd толқындық векторлар келесі түрде болады: k1x= k’1x= k2x= kx
Dne e
i ( wt k1 x x )
Dnr e
i ( wt k1 x x )
Dnd e i ( wt k2 x x )
n1
k’1
j
k1x
k’1x
k2x
kx
k1
y
n2>n1
k2
n2
6. Закон Снеллиуса
ПосколькуЗакон Снеллиуса
k1x= k’1x= k2x=
kx
w
w
k1 sin j k2 siny n1 sin j n2 siny
c
c
n1
k’1
j
n1
n2>n1
y
n2<n1
k1
7. Формулы Френеля 1
Е2
2
Н
2
(1)
2
Формулы Френеля 1
Граничные условия для тангенциальных составляющих
напряжённостей поля ЭМ волны поляризованной в плоскости
падения излучения.
для диэлектрика
H e+ H r= H d ;
Е е+Е r= Е d
1 E H nE
(2)
H e
He
j
H r
n1
Hr
Ee cos j Er cos j Ed cosy
(3)
Ee n1 Er n1 Ed n2
(4)
Ee cos j Er cos j cosy
Ee n1 Er n1
n2
(5)
Е е
n2
Е r
H d
Е d
y
Hd
8. Формулы Френеля 2
n2 Ee cos j n2 Er cos j Ee n1 cosy Er n1 cosy(1)
Формулы Френеля 2
n2 Ee cos j Ee n1 cosy n2 Er cos j Er n1 cosy n1 sinj n2 siny
Er || tg(j y )
Коэффициент
n2 cos j n1 cosy
E r E r ||
r|| (2) отражения r||
n2 cos j n1 cosy
Ee Ee ||
Ee || tg(j y )
амплитуды
Eeecos
cosjj EE
y Ed cos
cosyj
E
j
d cos
r cos
Ee nE
E2 r n1E e nE1 d n2
dn
1
n1
(3)
(4) Граничные условия с Еr в правой части
Амплитудный коэффициент пропускания ЭМ
волны поляризованной в плоскости падения
Ed Ed ||
2n1 cos j
2 sin j cos j
d||
n2 cos j n1 cosy cos(j y ) sin(j y ) Ee Ee ||
(5)
Запись в комплексной показательной форме, r – координата вдоль луча
Ĕr// = ř// * Ĕе//
( r|| Eo ) e
i wt k1r
i 0
r|| e Eo e
i wt k r
i ( k k
d|| e
Ed || d|| Ee|| (d|| Eo ) e
2
d|| d|| e i ( k1 k2 ) r (8)
r – координата вдоль луча
1
2 )r
i wt k1r
Eo e
i wt k1r
(6)
(7)
9. Формулы Френеля 3
Граничные условия для тангенциальных составляющих напряжённостей поля ЭМволны поляризованной перпендикулярно плоскости падения излучения.
H e+ H r= H d ; Е е-Е r= Е d
Ee Er Ed (2)
Ee n1 cos j Er n1 cos j Ed n2 cosy
(1)
Ee n1 cos j Er n1 cos j n2 cosy
Ee E r
1 (3)
E e
Ee
j
Er
E r
Формулы Френеля 3
n1
H е
n2
H r
E d
H d
y
Ed
10. Формулы Френеля 4
Волна поляризована перпендикулярно плоскости падения.Коэффициент
E
n1 cos j n2 cosy
E
r r r отражения r
n1 cos j n2 cosy
Ee Ee (1) амплитуды
sin(j y ) i
r
e
sin(j y ) (3)
Формулы Френеля 4
Er
sin(j y )
Ee
sin(j y )(2)
Амплитудный коэффициент пропускания ЭМ
волны поляризованной перпендикулярно
плоскости падения
Ed Ed
2n1 cos j
2 sin j cos j
d
n1 cos j n2 cosy
sin(j y )
E e E e |
(4)
Запись в комплексной показательной форме
Ĕr = ř * Ĕе
(5)
sin(j y )
i wt k1r sin(j y ) i
E0 e
e Eo e i wt k1r
sin(j y )
(6)
sin(j y )
Ed d Ee (7) d d e i ( k k ) r (8)
1
(d Eo ) e
i wt k2 r
2
d e
i ( k1 k2 ) r
Eo e
i wt k1r (9)
11.
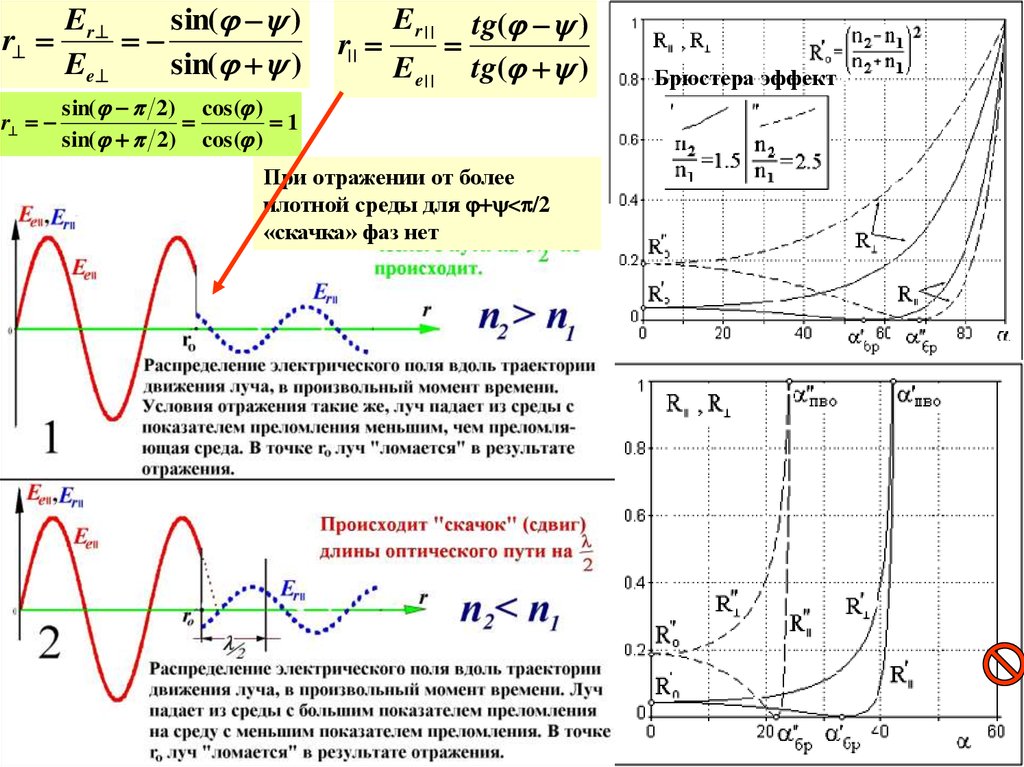
12. Брюстера эффект
Ersin(j y )
r
Ee
sin(j y )
r
sin(j 2) cos(j )
1
sin(j 2) cos(j )
r||
Er ||
Ee ||
tg(j y )
tg(j y )
При отражении от более
плотной среды для j y< /2
«скачка» фаз нет
Брюстера эффект








 Физика
Физика








