Физика рассеяния света

1. Теоря Gustav Mie

Будак Владимир Павлович,
Национальный исследовательский
университет «МЭИ»
кафедра светотехники
: +7 (495) 763-5239
BudakVP@mpei.ru

2. Диэлектрические шары без поглощения

0
∞
x
1
12
1
61
2
23
6
n
область
G.Mie
3
56
5
∞
45
4
34
2m 1
am m ( ) bm m ( )
m
(
m
1)
m 1
S1 ( )
области, отмеченные одной цифрой, определяются одним, ярко
выраженным эффектом
области,
отмеченные
двумя
цифрами, занимают промежуточное положение, где имеют
место эффекты обоих областей
Только последние годы расчеты по теории Mie
стали делом заурядным

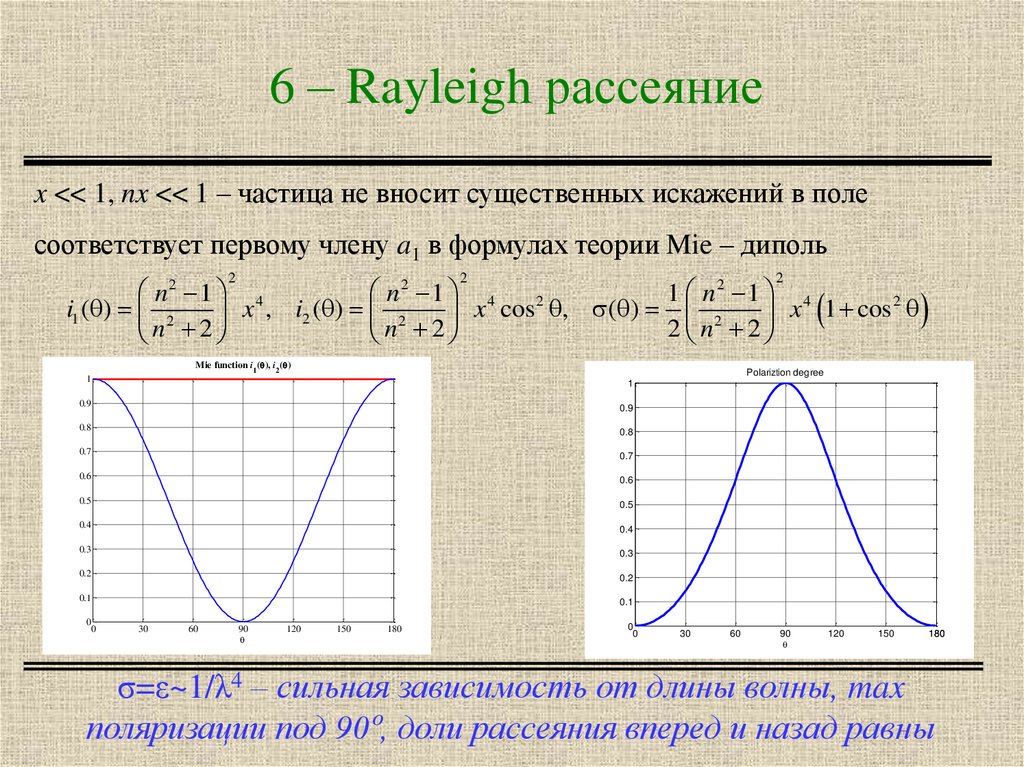
3. 6 – Rayleigh рассеяние

x << 1, nx << 1 – частица не вносит существенных искажений в поле
соответствует первому члену a1 в формулах теории Mie – диполь
2
2
2
n2 1 4
n2 1 4
1 n2 1 4
2
2
i1 ( ) 2
x , i2 ( ) 2
x cos , ( ) 2
x 1 cos
2 n 2
n 2
n 2
Mie function i1( ), i2( )
Polariztion degree
1
1
0.9
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
0
0
30
60
90
120
150
180
0
0
30
60
90
120
150
180
σ=ε~1/λ4 – сильная зависимость от длины волны, max
поляризации под 90º, доли рассеяния вперед и назад равны

4. 56 – Рост размеров частиц

С ростом размеров частиц необходимо учитывать все большее
число членов ряда. что приводит:
1. вперед/назад > 1 – рост доли рассеянного вперед – эффект
Mie
2. максимум поляризации смещается в область углов θ>90º и
уменьшается (<1)
3. остаточный голубой свет при 90º - i1 и i2 неодинаково зависят
от длины волны
Релеевское рассеяние не чувствительно ни к форме,
ни к размерам частиц

5. 5 – оптический резонанс

с дальнейшим ростом оптических размеров частицы наиболее
существенными становятся члены с большими номерами
периодически возникают стоячие волны в частице, для
которых наблюдается оптический резонанс – стоячие волны,
удерживаемые на шаре
am
m ( y ) m ( x) n m ( y ) m ( x)
n m ( y) m ( x) m ( y) m ( x)
, bm
m ( y ) m ( x) n m ( y ) m ( x)
n m ( y) m ( x) m ( y) m ( x)
На кривой ослабления пики, индикатриса рассеяния и кривая
поляризации приобретает крайне сложный, капризный вид

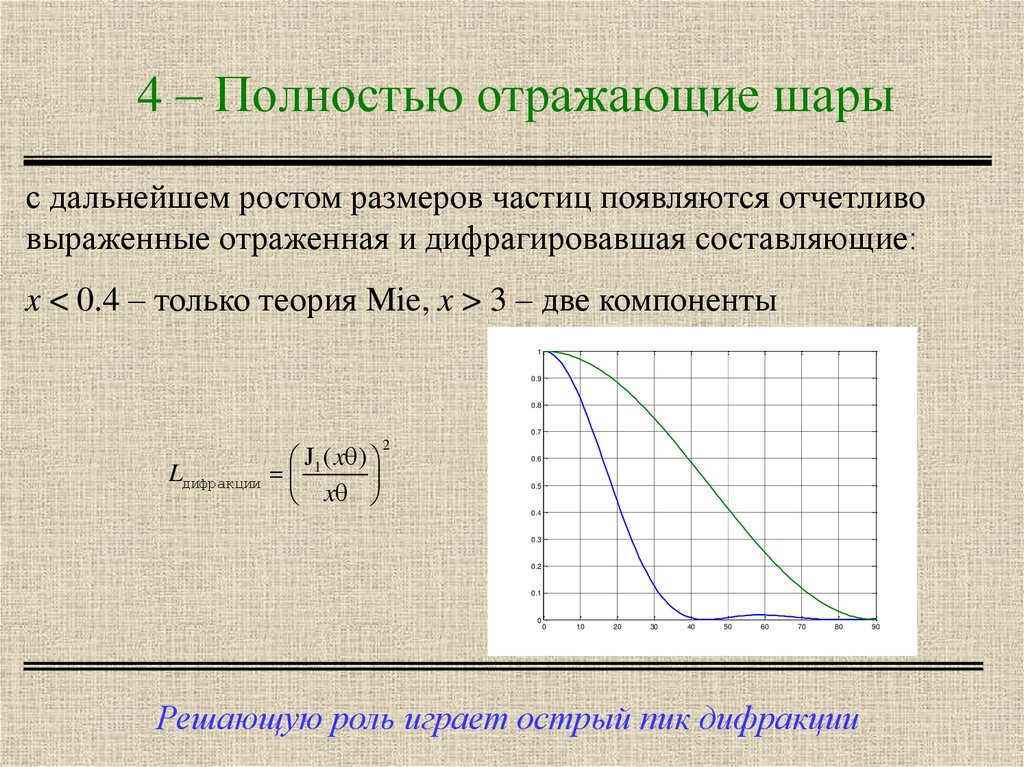
6. 4 – Полностью отражающие шары

с дальнейшем ростом размеров частиц появляются отчетливо
выраженные отраженная и дифрагировавшая составляющие:
x < 0.4 – только теория Mie, x > 3 – две компоненты
1
0.9
0.8
0.7
J ( x )
Lдифракции 1
x
2
0.6
0.5
0.4
0.3
0.2
0.1
0
0
10
20
30
40
50
60
70
80
Решающую роль играет острый пик дифракции
90

7. 3 – область геометрической оптики

с уменьшением показателя преломления n появляется все более
выраженная преломленная компонента
геометрическая оптика (отражение+преломление) + дифракция
отраженная и преломленная компоненты сильно поляризованы
Qe = 2 – парадокс рассеяния
радуга
глория
Радуги, глории не могут быть вычисленны в приближении ГО

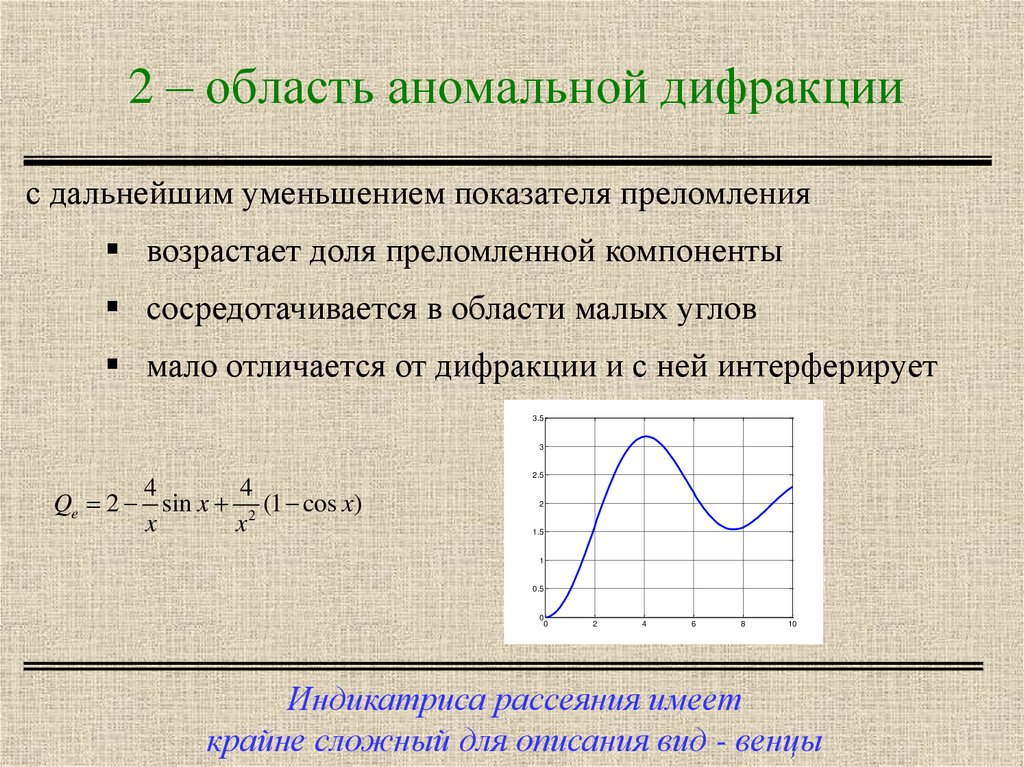
8. 2 – область аномальной дифракции

с дальнейшим уменьшением показателя преломления
возрастает доля преломленной компоненты
сосредотачивается в области малых углов
мало отличается от дифракции и с ней интерферирует
3.5
3
4
4
Qe 2 sin x 2 (1 cos x)
x
x
2.5
2
1.5
1
0.5
0
0
2
4
6
8
10
Индикатриса рассеяния имеет
крайне сложный для описания вид - венцы

9. 1 – область Rayleigh-Hans

уменьшение размеров приводит
к уменьшению фазового сдвига между преломленной и
отраженной компонентами
уменьшает дифракцию
компоненты становятся неразличимы
каждый элемент объема рассеивает по Rayleigh, а
суммарная волна – интерференция волн от этих
элементов
Расчет возможен для частиц произвольной формы

10. Влияние других факторов

1.
поглощение n+iκ – очень сильное на все характеристики рассеяния,
даже в малых количествах, качественно связано с уменьшением доли
преломленного света и увеличением отраженного
2.
форма – особенно сильно на область рассеяния назад, и на
поляризацию;
совокупность
хаотически
ориентированных
несферических частиц не эквивалентна системе сферических
3.
полидисперсность – приводит к сглаживанию всех интерференционных
эффектов
1 x2
2
2 r
2 r
n ( r )
dr
C
r
dr
r 0 2
r1
1
r2
r
n( r )
dN
C0 r
dr
1
n
(
x
)
x
dx
Const
x1
распределение Юнге
Рассеяние на аэрозоле имеет все более неселективный характер