Прохождение излучения через границу раздела двух сред

1. ФОТОНИКА

1
ФОТОНИКА
Лекция 3
Прохождение излучения
через границу раздела
двух сред

2. Отражение и преломление излучения на границе раздела двух сред

2
Отражение и преломление излучения
на границе раздела двух сред
z
N
2
t
n
n
x
i
r
1
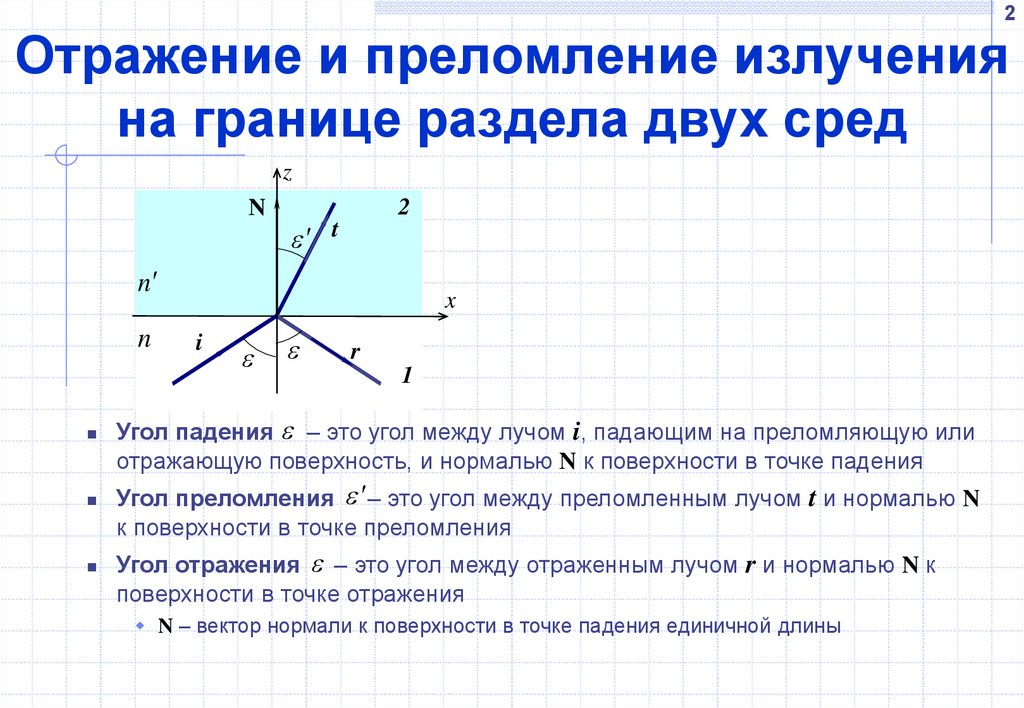
Угол падения – это угол между лучом i, падающим на преломляющую или
отражающую поверхность, и нормалью N к поверхности в точке падения
Угол преломления – это угол между преломленным лучом t и нормалью N
к поверхности в точке преломления
Угол отражения – это угол между отраженным лучом r и нормалью N к
поверхности в точке отражения
N – вектор нормали к поверхности в точке падения единичной длины

3. Закон преломления

3
Закон преломления
Уравнение падающей плоской волны:
ik q , r
U i r U i e 0 i
Уравнение преломленной плоской волны:
ik q , r
U t r U t e 0 t
Уравнение отраженной плоской волны:
ik q , r
U r r U r e 0 r
где q i, q t, q r – оптические векторы падающей, отраженной и
преломленной волн, k 0 – волновое число, r – радиус-вектор произвольной
точки

4. Закон преломления в векторной форме

4
Закон преломления
в векторной форме
На границе раздела двух сред:
qi , r q t , r
Равенство соблюдается для всех r, перпендикулярных
вектору нормали:
q t , r qi , r 0 при r, N 0
или:
q t qi , r 0 при r, N 0
или:
q t qi r при N r
Выполнение этих условий возможно если:
qt qi || N

5. Закон преломления в векторной форме

5
Закон преломления
в векторной форме
Закон преломления в векторной форме:
qt qi N
где Г – некоторый скаляр
или:
qt N qi N
или:
q t qi N 0

6. Закон преломления в векторной форме

6
Закон преломления
в векторной форме
Чтобы найти Г, домножим скалярно выражение закона
преломления на вектор нормали:
N q N q N N
N N 1 , следовательно
q q N
где n cos n cos
n cos n cos

7. Классический закон преломления

7
Классический закон преломления
Качественная часть закона:
падающий луч, преломленный луч и нормаль к
поверхности раздела двух сред в точке падения лежат в
одной плоскости
Количественная часть закона:
произведение показателя преломления на синус угла
между лучом и нормалью остается постоянным при
переходе в следующую среду:
n sin n sin

8. Закон отражения

8
Закон отражения
Закон отражения:
sin( ) sin
N
2
t
n
n
i
r
1
Закон отражения как частный случай закона преломления
при n n :
q r qi N
где 2n cos
n
n n

9. Полное внутреннее отражение

9
Полное внутреннее отражение
Условие полного внутреннего отражения (ПВО):
sin
n'
n
ПВО позволяет решить задачу полного
отражения света
(при ПВО отражается 100% энергии, то есть
потерь энергии нет)
нарушенное полное внутреннее отражение
(НПВО) – возникает при ПВО вследствие
наличия поглощения в приграничном слое при
оптическом контакте границы раздела со
средой, используется в спектроскопии для
изучения свойств поглощающих сред
2
n n
n
1

10. Формулы Френеля

10
Формулы Френеля
Электрический вектор падающей плоской волны E i можно
разложить на две составляющие:
A | | – лежит в плоскости падения
A – перпендикулярна плоскости падения
z
r
n
n
A||
i
t
T||
T
x
R
R ||
r

11. Формулы Френеля

11
Формулы Френеля
Компоненты электрического вектора поля падающей
плоской волны:
E x(i ) A | | cos
E y( i ) A
E z(i ) A | | sin
Компоненты магнитного вектора поля падающей плоской
волны:
H x( i ) A n cos
H y(i ) A | | n
H z( i ) A n sin

12. Формулы Френеля

12
Формулы Френеля
Поле прошедшей волны:
E x(t ) T | | cos
H x( t ) T n' cos '
E y( t ) T
H y( t ) T | | n
E z(t ) T | | sin
H z( t ) T n ' sin '
Поле отраженной волны:
E x( r ) R | | cos r
H x( r ) R n cos r
E y( r ) R
H y( r ) R | | n
E z( r ) R | | sin r
H z( r ) R n sin r

13. Формулы Френеля

13
Формулы Френеля
На границе раздела двух сред должны выполняться
соотношения:
E x( i ) E x( r ) E x( t )
H x( i ) H x( r ) H x( t )
E y(i ) E y( r ) E y( t )
H y(i ) H y( r ) H y( t )
описывают непрерывность тангенциальных компонент электрического и
магнитного полей, если поглощения на границе нет
Подставив значения всех компонент, и учитывая, что
cos r cos cos получим:
cos A | | R | | cos T | |
A R T
n cos A R n cos T
n A | | R | | n T | |

14. Формулы Френеля

14
Формулы Френеля
Формулы Френеля, для амплитуд прошедшей T | | , T и
отраженной R | | , R волн:
2n cos
T
| | n cos n cos A | |
2n cos
A
T
n cos n cos
n cos n cos
R | | n cos n cos A | |
n cos n cos
R
A
n cos n cos
или:
2 sin cos
T
| | sin cos A | |
2 sin cos
T
A
sin
tg
R | | tg A | |
sin
R
A
sin

15. Распределение энергии между отраженным и преломленным полями

15
Распределение энергии между
отраженным и преломленным полями
Интенсивности падающей, прошедшей и отраженной
волн:
I i ~ A2 cos n
2
2
I t ~ T 2 cos n
I r ~ R 2 cos n
2

16. Распределение энергии между отраженным и преломленным полями

16
Распределение энергии между
отраженным и преломленным полями
Коэффициент отражения показывает, какая часть
энергии отражается по отношению к падающей:
R 2 n cos
R2
2
2
2
A
A n cos
2
Коэффициент пропускания показывает, какая часть
энергии проходит по отношению к падающей:
2
n cos T 2
2
2
n cos A
в сумме коэффициенты отражения и пропускания равны единице:
1

17. Распределение энергии между отраженным и преломленным полями

17
Распределение энергии между
отраженным и преломленным полями
Коэффициенты отражения и пропускания зависят от
направления поляризации падающей волны:
sin 2 sin
tg 2
|| 2
| | 2
tg
sin cos2
2
2
sin
sin
sin
sin 2
sin 2
при прохождении светом границы раздела двух сред его состояние
поляризации изменяется

18. Нормальное падение

18
Нормальное падение
При нормальном падении 0
Коэффициент отражения:
n n
| |
n n
2
Коэффициент пропускания:
4
n
n
4nn
2
2
n
n
n
1
n
при нормальном падении света на границу стекло-воздух
(отражается около 4% энергии)
0.04

19. Угол Брюстера

19
Угол Брюстера
tg 2 :
| | 2
tg
При условии
/ 2
:
tg
Угол, при котором происходит
полная (линейная) поляризация
при отражении, называется
углом Брюстера:
tg
n
n
и || 0
N
n
n
i
t
2
r

20. Угол Брюстера

20
Угол Брюстера
График зависимости коэффициентов отражения
для TM и TE поляризованного света от угла падения
ТЕ – состояние поляризации, при
которой электрический вектор
перпендикулярен плоскости падения ( E )
1
0.9
ТМ – состояние поляризации, при
которой электрический вектор
лежит в плоскости падения ( E | | )
0.8
0.7
0.6
0.5
TE
0.4
0.3
TM
0.2
i
0.1
0
0
10
20
30
40
50
56
60
70
80
90

21. Типы поляризации света

21
Типы поляризации света
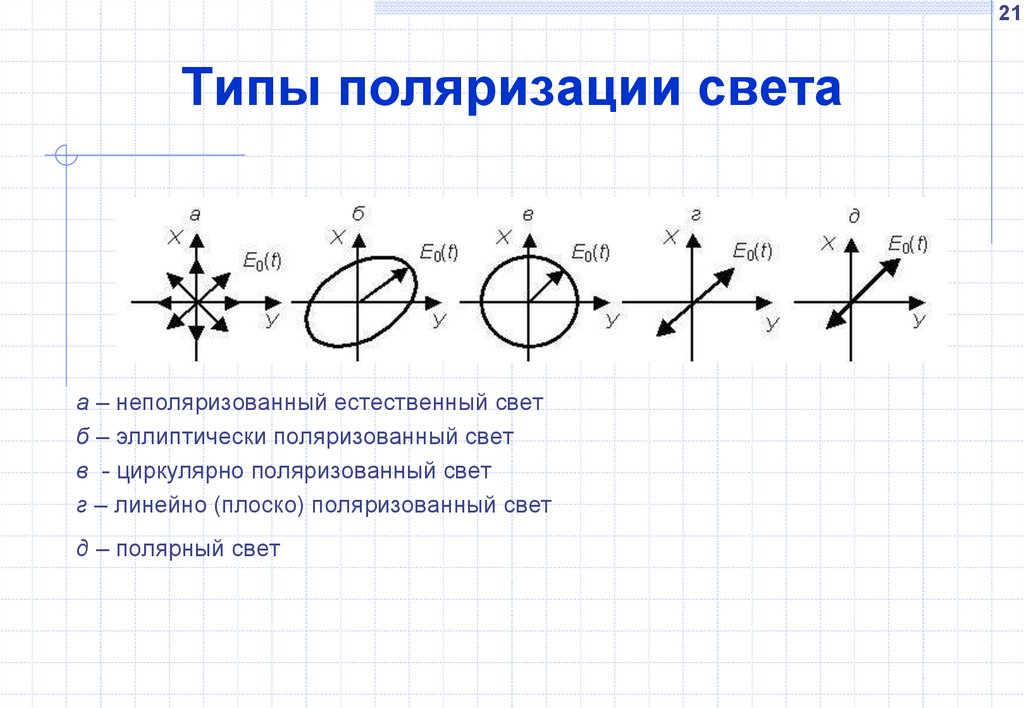
а – неполяризованный естественный свет
б – эллиптически поляризованный свет
в - циркулярно поляризованный свет
г – линейно (плоско) поляризованный свет
д – полярный свет

22. Применения поляризации

22
Применения поляризации
Исследование напряжения в материалах
(двулучепреломление)
Подавление паразитных отражений при фотосъемке,
наблюдении через солнцезащитные очки
Изменение оптической активности жидкокристаллических
элементов (Twisted Nematic Display)
Количественный анализ растворов оптически активных
веществ
Микроскопические исследования очень малых частиц
Эллипсометрические исследования структуры слоев

23. Просветление оптики. Тонкие пленки

23
Просветление оптики.
Тонкие пленки
Просветление оптики – применение тонкослойных
пленок (интерференционных покрытий) для ослабления
френелевского отражения
Амплитуды отраженных волн от границ раздела
воздух–пленка и пленка–стекло должны быть равны:
R1 R2
Фазы (эйконалы) должны отличаться на половину периода:
E1 E2
1 2
2
n0 nпл ncт
Для этого необходимо выполнение
условий: n n n
пл
ст
n пл d пл
cp
4
dпл
воздух
стекло
пленка