Похожие презентации:
Свойства и признаки параллелограмма
1. Свойства и признаки параллелограмма
Автор: Гурьева Наталья Николаевна,учитель математики,
МКОУ СОШ №26 п.Кропачёво,
Ашинского района,
Челябинской области
2.
СВОЙСТВАВ параллелограмме
противоположные стороны и
противоположные углы равны
В параллелограмме сумма
углов, прилежащих к одной
стороне, равна 180°.
Диагонали параллелограмма
точкой пересечения делятся
пополам.
ПРИЗНАКИ
Если в четырехугольнике
противоположные стороны
равны и параллельны, то этот
четырехугольник является
параллелограммом.
Если в четырехугольнике
противоположные стороны
попарно равны, то этот
четырехугольник является
параллелограммом.
Если в четырехугольнике
диагонали точкой пересечения
делятся пополам, то этот
четырехугольник является
параллелограммом.
3. Ответь на вопросы:
Какие углы образуются при параллельных прямых?
Каковы их свойства?
Какой треугольник называется равнобедренным?
Каковы свойства углов равнобедренного треугольника?
Какова сумма углов прямоугольного треугольника?
Что вы знаете о катете, лежащим против угла в 30°?
Назовите признаки равенства треугольников?
Перечислите свойства параллелограмма.
Перечислите признаки параллелограмма.
4. Выбери задание:
12
3
4
5
6
7
8
9
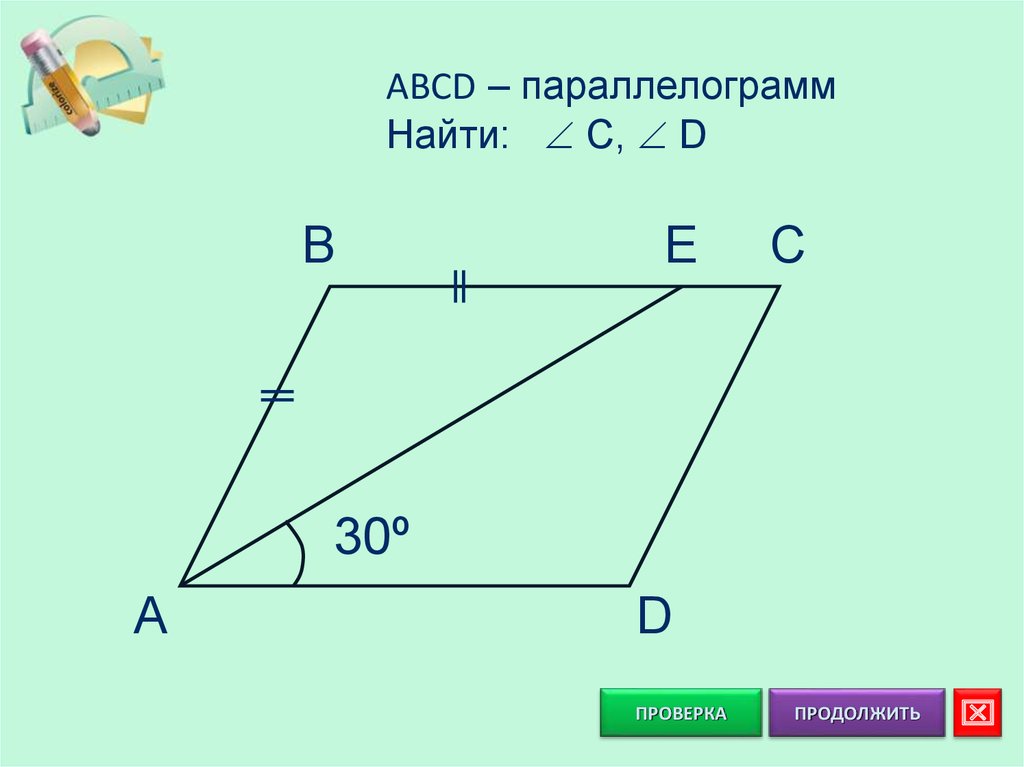
5. ABCD – параллелограмм Найти: C, D
ABCD – параллелограммНайти: C, D
B
E
C
30º
A
D
ПРОВЕРКА
ПРОДОЛЖИТЬ
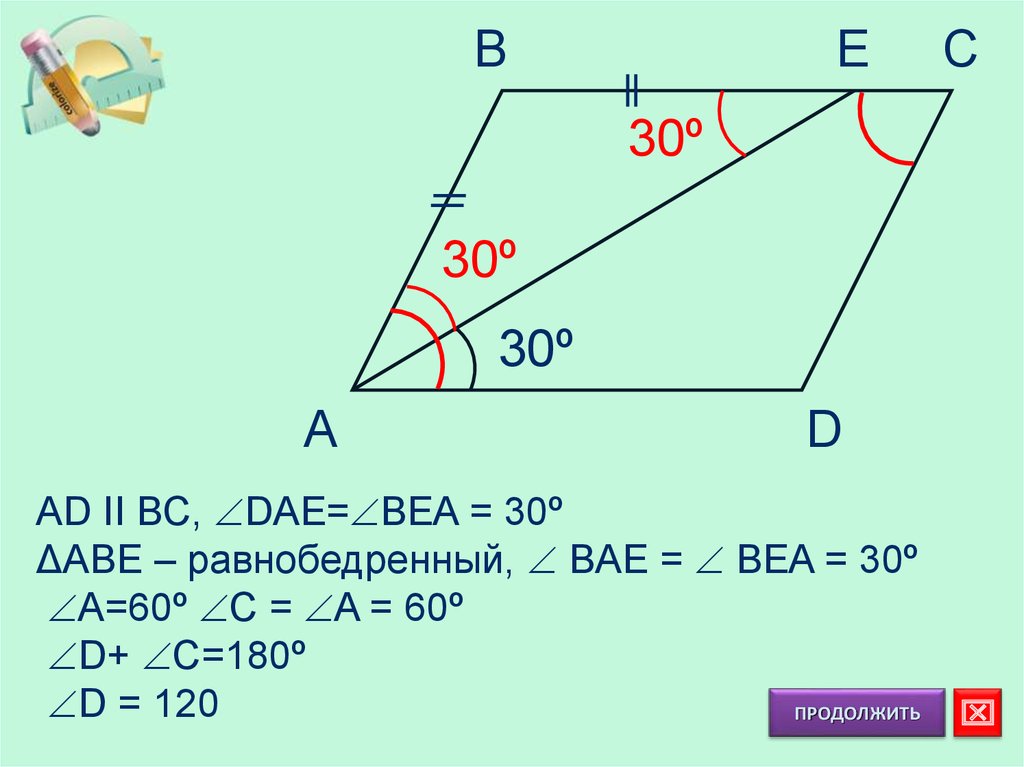
6.
BE
C
30º
30º
30º
A
D
AD II BC, DAE= BEA = 30º
ΔABE – равнобедренный, BAE = BEA = 30º
A=60º C = A = 60º
D+ C=180º
D = 120
ПРОДОЛЖИТЬ
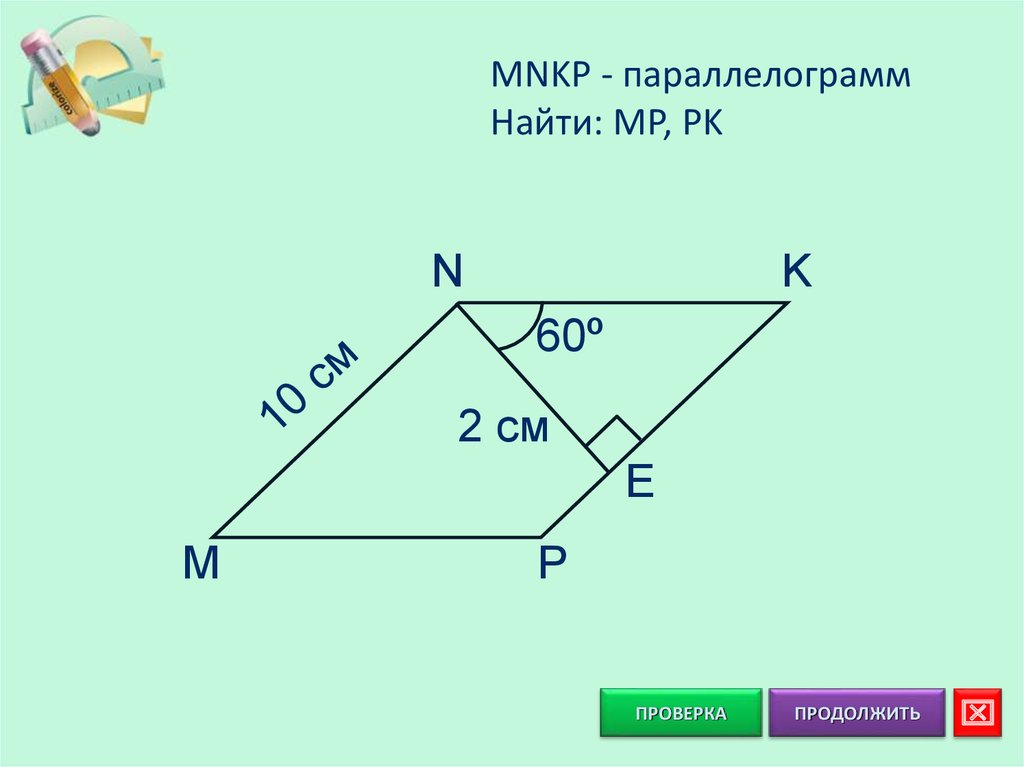
7. MNKP - параллелограмм Найти: MP, PK
NK
60º
2 см
E
M
P
ПРОВЕРКА
ПРОДОЛЖИТЬ
8.
NK
4
60º
30º
2 см
E
M
4
P
K=30º, значит NE=0,5·NK
NK= 4 см
MP = NK = 4 см
MN = PK = 10 см
ПРОДОЛЖИТЬ
9.
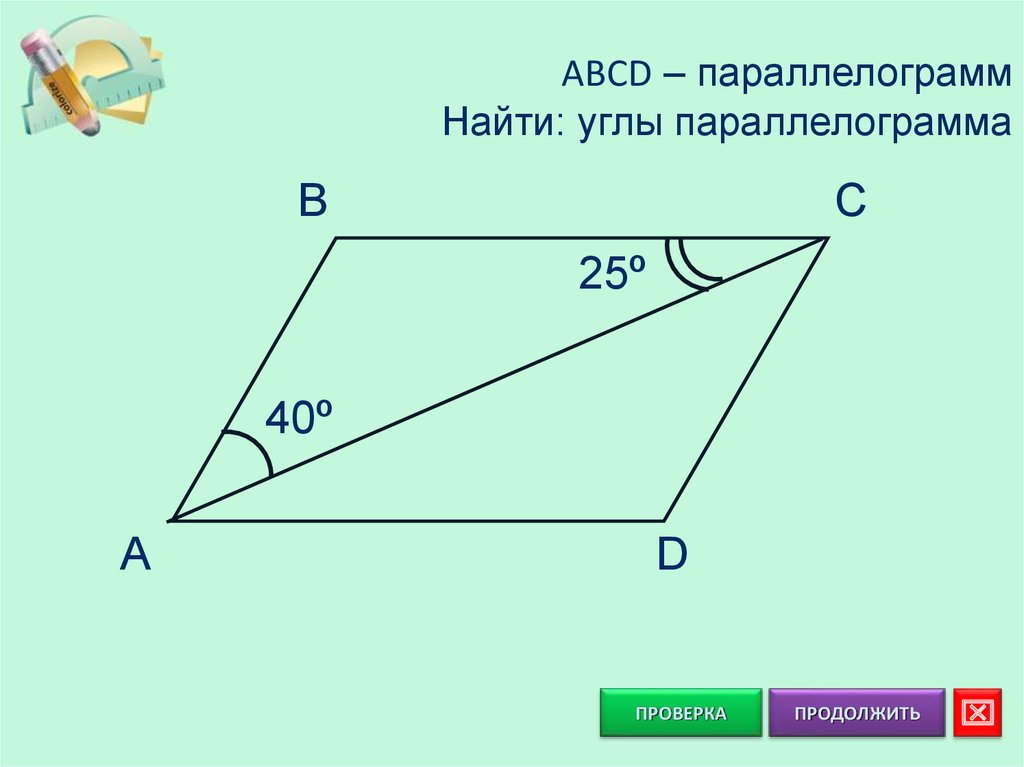
ABCD – параллелограммНайти: углы параллелограмма
B
C
25º
40º
A
D
ПРОВЕРКА
ПРОДОЛЖИТЬ
10.
BC
115º
25º
25º
115º
40º
A
D
BCA = CAD = 25°
A = 40°+25°=65°
A= C=65°
В= D=180°- 65°=115°
ПРОДОЛЖИТЬ
11.
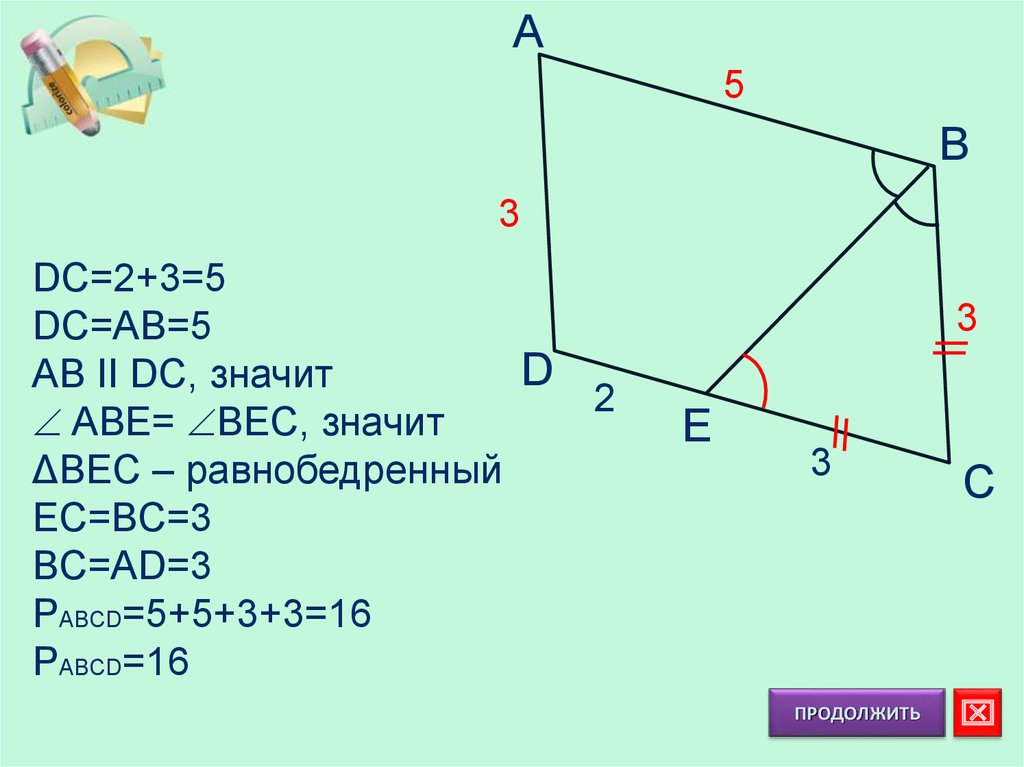
ABCD – параллелограммНайти: PABCD
A
B
D
2
E
3
C
ПРОВЕРКА
ПРОДОЛЖИТЬ
12.
A5
B
3
DC=2+3=5
DC=AB=5
D
AB II DC, значит
2
ABE= BEC, значит
ΔBEC – равнобедренный
EC=BC=3
BC=AD=3
PABCD=5+5+3+3=16
PABCD=16
3
E
3
ПРОДОЛЖИТЬ
C
13.
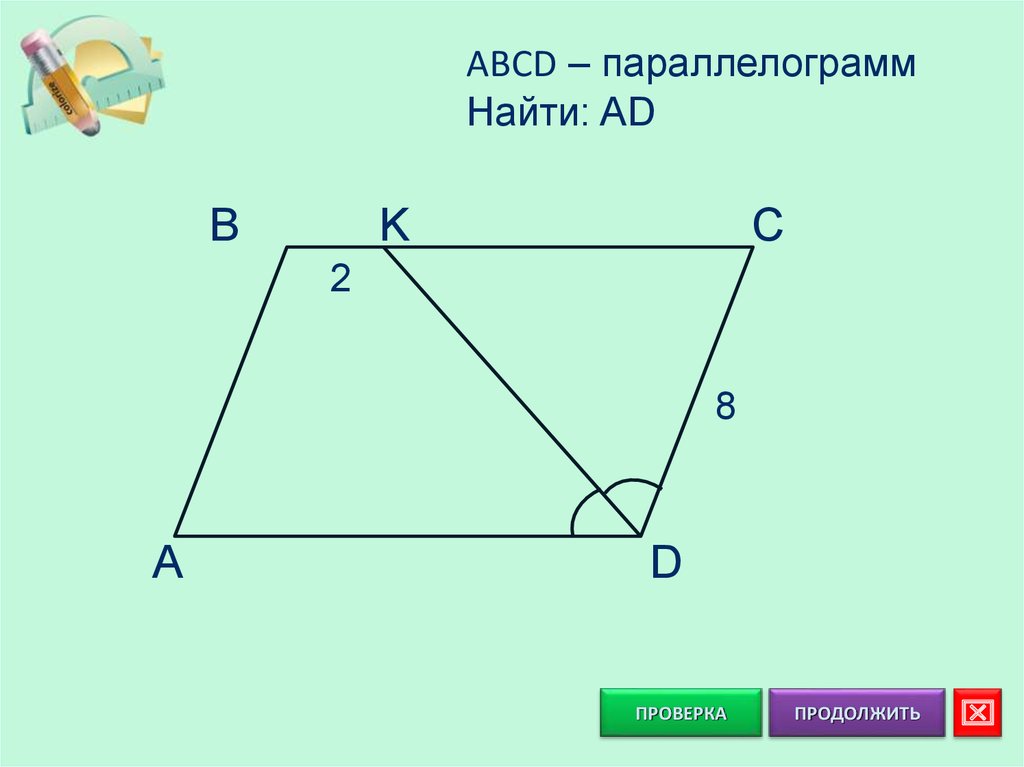
ABCD – параллелограммНайти: AD
B
K
C
2
8
A
D
ПРОВЕРКА
ПРОДОЛЖИТЬ
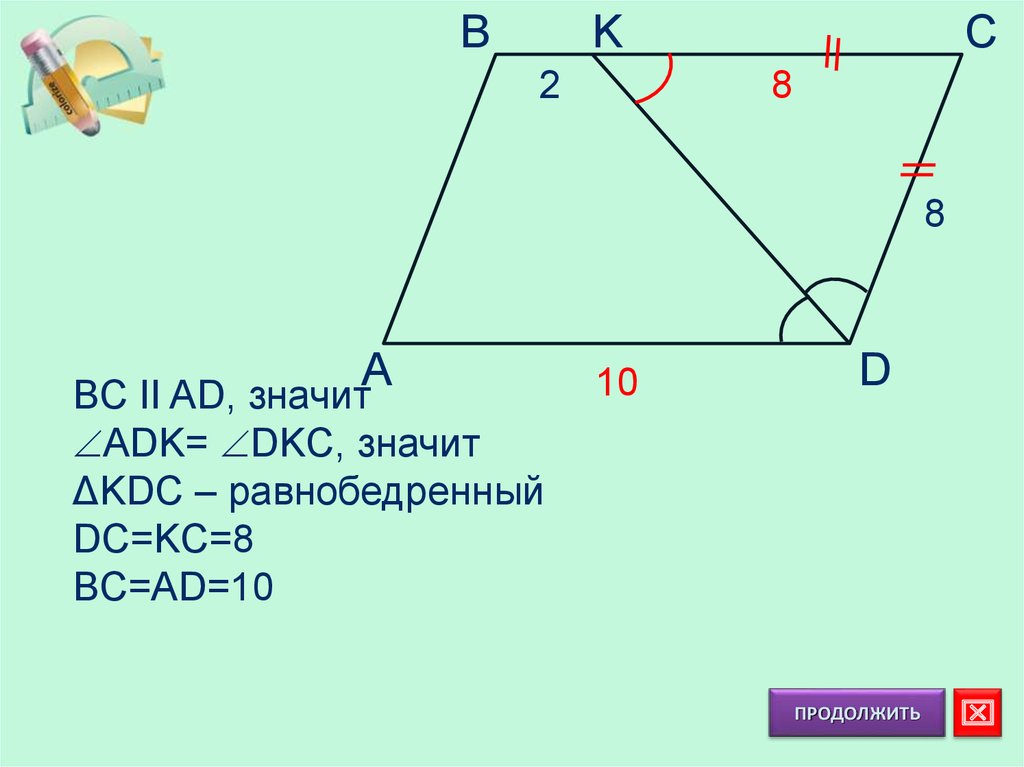
14.
BK
2
C
8
8
A
BC II AD, значит
ADK= DKC, значит
ΔKDC – равнобедренный
DC=KC=8
BC=AD=10
10
D
ПРОДОЛЖИТЬ
15.
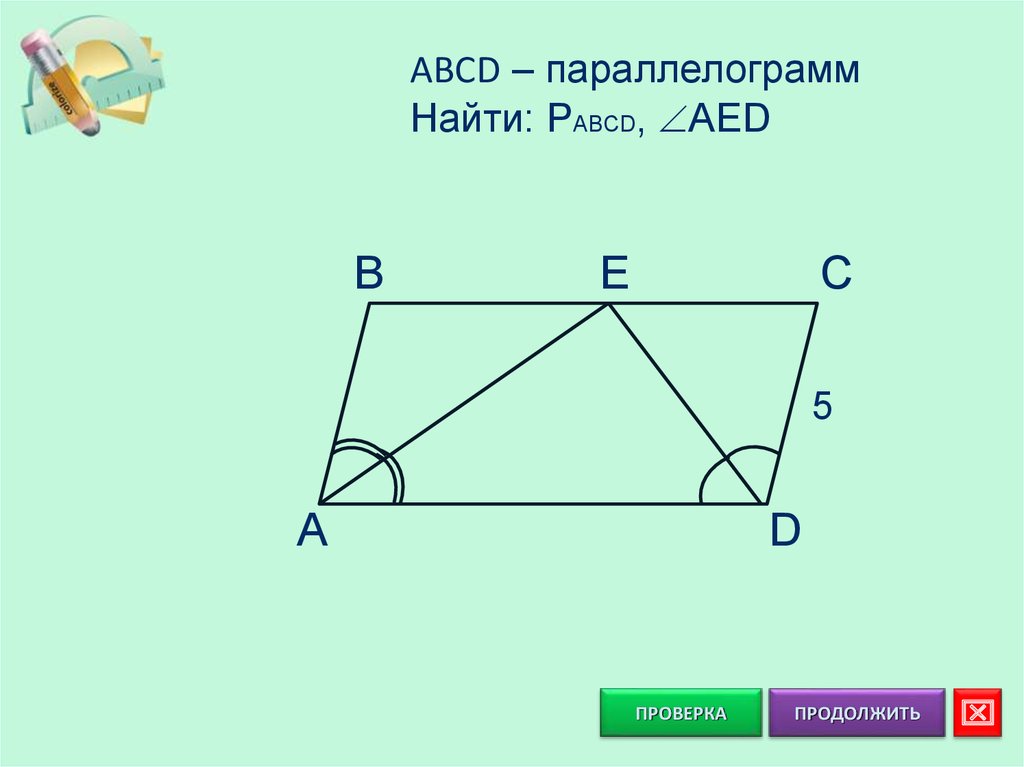
ABCD – параллелограммНайти: PABCD, AED
B
E
C
5
A
D
ПРОВЕРКА
ПРОДОЛЖИТЬ
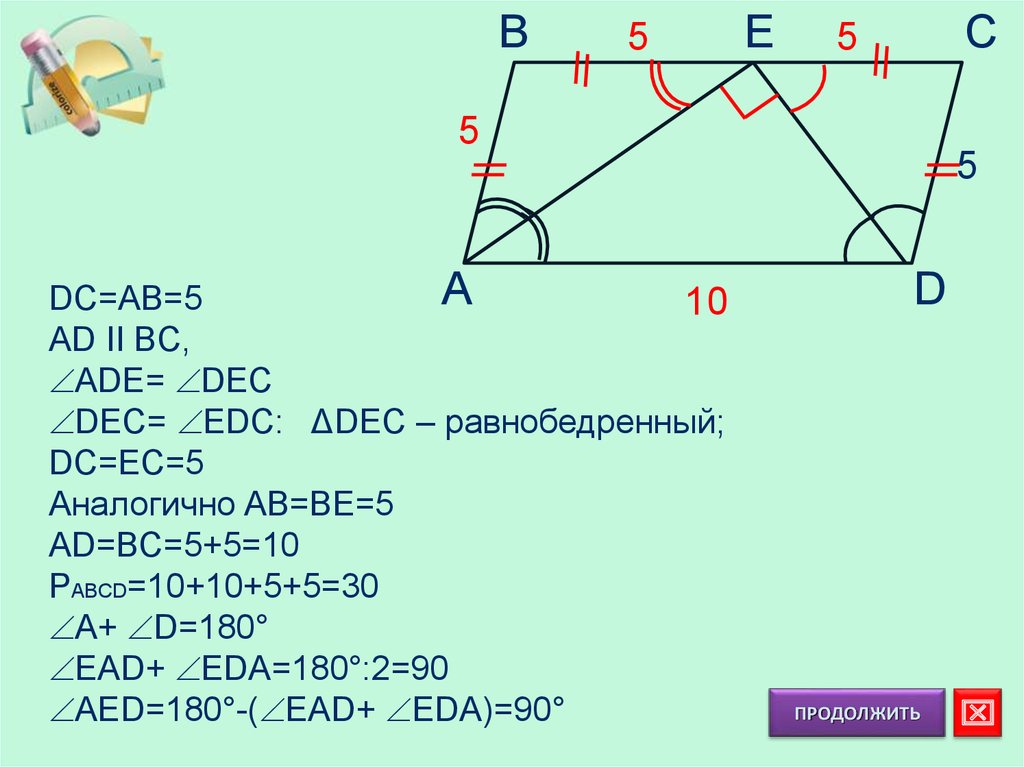
16.
B5
E
C
5
5
A
DC=AB=5
10
AD II BC,
ADE= DEC
DEC= EDC: ΔDEC – равнобедренный;
DC=EC=5
Аналогично AB=BE=5
AD=BC=5+5=10
PABCD=10+10+5+5=30
A+ D=180°
EAD+ EDA=180°:2=90
AED=180°-( EAD+ EDA)=90°
5
D
ПРОДОЛЖИТЬ
17.
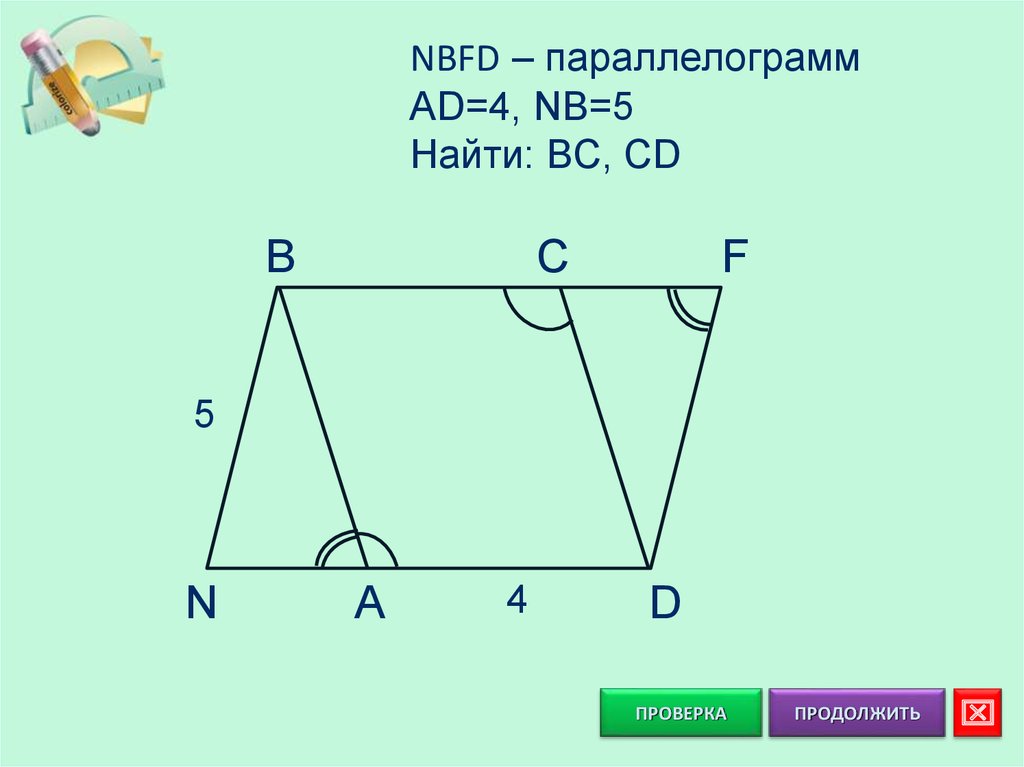
NBFD – параллелограммAD=4, NB=5
Найти: BC, CD
B
C
F
5
N
A
4
D
ПРОВЕРКА
ПРОДОЛЖИТЬ
18.
4B
5
5
N
A
F= N: NB=AB=5
BC II AD: FCD= CDA
BCD= BAD:
BAN= FCD
BAN= CDA: AB II CD
ABCD – параллелограмм
BA=CD=5
AD=BC=4
C
F
5
4
D
ПРОДОЛЖИТЬ
19.
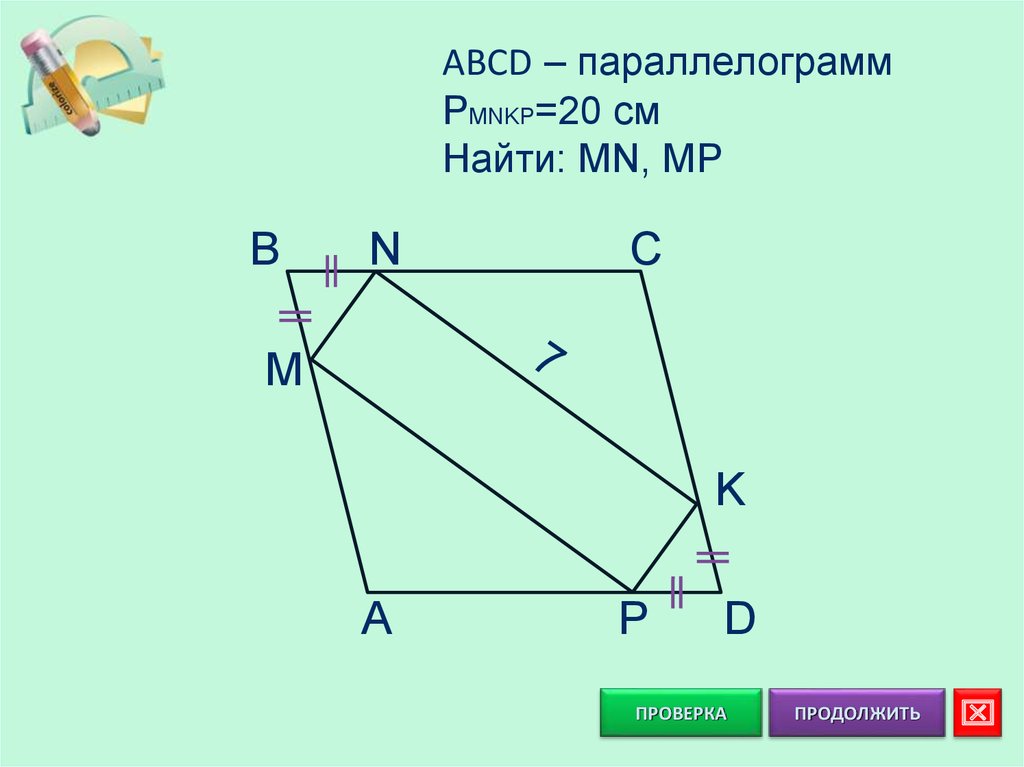
ABCD – параллелограммPMNKP=20 см
Найти: MN, MP
B
N
C
M
K
A
P
D
ПРОВЕРКА
ПРОДОЛЖИТЬ
20.
BN
C
M
B= D
ΔMBN=ΔKDP: MN=PK
BC=AD: NC=AP,
AB=CD: AM=CK,
A= C: ΔNCK=ΔPAM:
NK=NP
MNKP – параллелограмм
NK=MP=7
MN=(20-14):2=3
K
A
P
ПРОДОЛЖИТЬ
D
21.
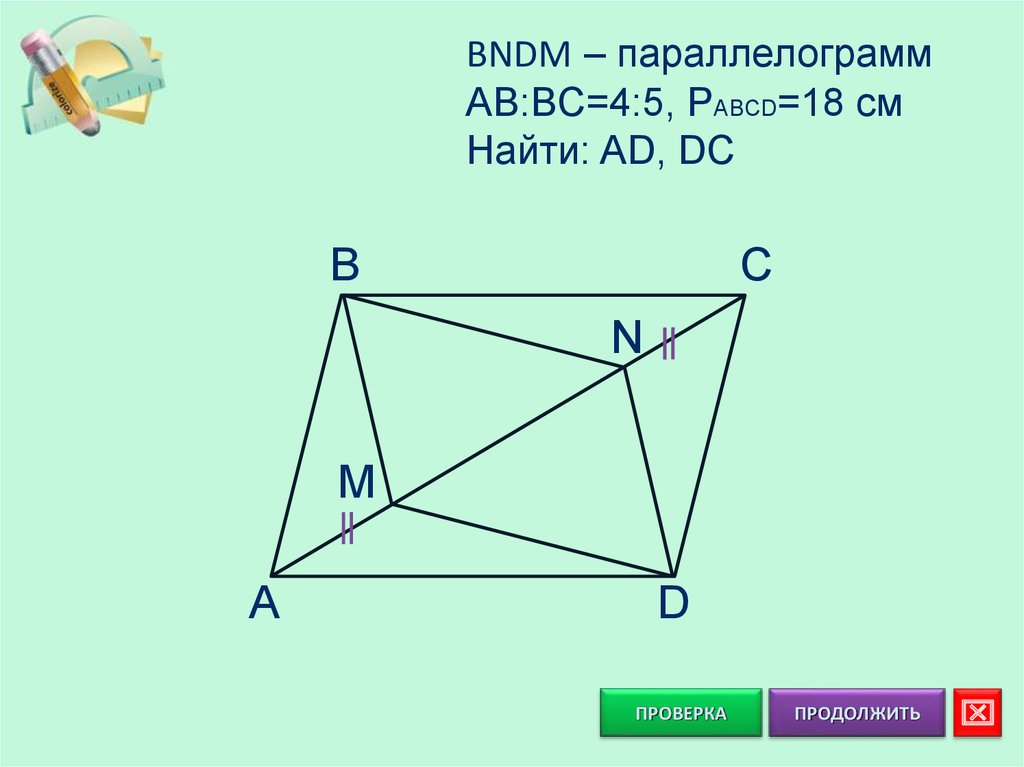
BNDM – параллелограммAB:BC=4:5, PABCD=18 см
Найти: AD, DC
B
C
N
M
A
D
ПРОВЕРКА
ПРОДОЛЖИТЬ
22.
B5
C
N
4
AM=NC; BM=ND;
BM II ND: AMB= CND
ΔAMB=ΔCND: AB=CD
Аналогично
ΔBNC=ΔDMA: BC=AD A
ABCD – параллелограмм
4х+4х=5х+5х=18
18х=18
х=1
AB=DC=4 см
BC=AD=5 см
4
M
5
D
ПРОДОЛЖИТЬ
23. Использована литература:
• Атанасян Л.С. и др. Геометрия: Учебник для7-9 классов общеобразовательных
учреждений. – М.: Просвещение, 2013 г.
• Гаврилов Н.Ф. Поурочные разработки по
геометрии: 8 класс. – М.:ВАКО, 2009 г.











 Математика
Математика








