Информация из оптимальной Симплекс-таблицы

1.

Информация
из
оптимальной
Симплекс-таблицы
Оптимальное
решение
Статус ресурсов
Ценность каждого
ресурса
Чувствительность
оптимального
решения

2. Ценность ресурса

Ценность ресурса – характеризуется величиной улучшения
оптимального значения f , приходящегося на единицу прироста
данного ресурса

3.

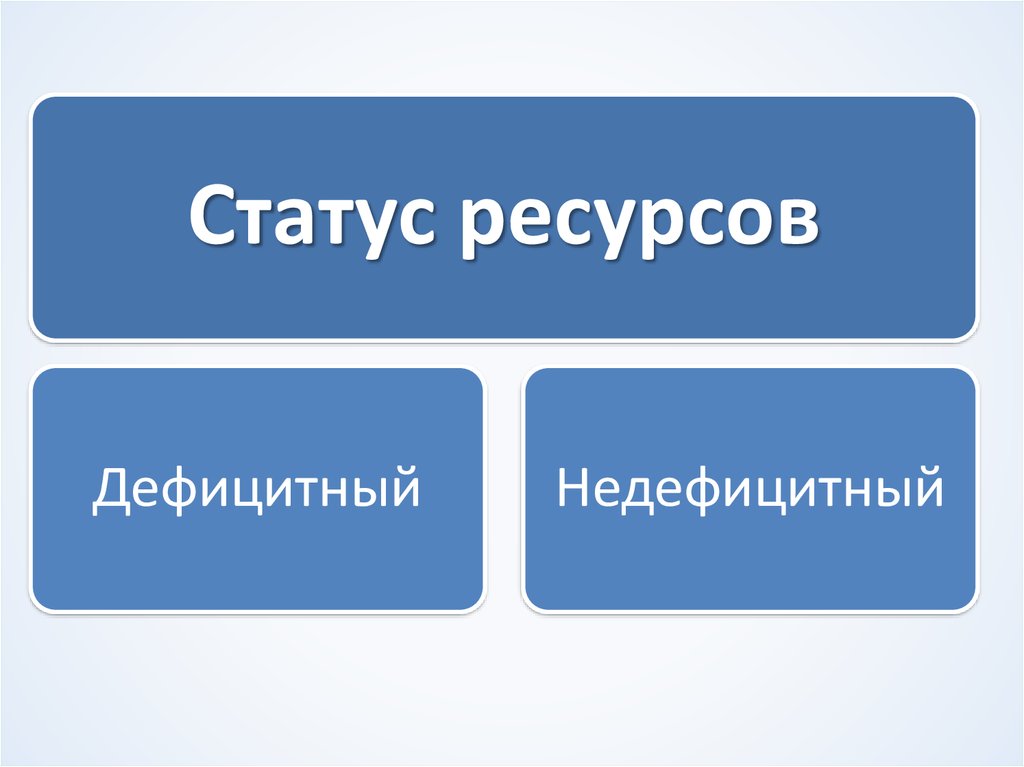
Статус ресурсов
Дефицитный
Недефицитный

4. Теория двойственности

Определение. Парой симметричных двойственных задач
называются задачи
f ( x) (c, x) max
Ax b
x 0
g ( y ) (b, y ) min
(1)
y 0
A y c
T
Задачи (1), (2) являются взаимно двойственными
задачами.
( 2)

5. Теоремы двойственности

Теорема 1 (Первая теорема двойственности). Двойственные
задачи одновременно разрешимы или не разрешимы, и в случае
их разрешимости оптимальные значения целевых функций
совпадают.
Следствие 1. Если исходная задача является задачей в
канонической форме и ее оптимальная симплекс таблица
известна, то оптимальное решение двойственной задачи есть
( y* , A j ) j c j
Следствие 2. Если исходная задача является задачей в
стандартной форме и ее оптимальная симплекс таблица известна,
то оптимальное решение двойственной задачи есть
yi* ui

6. Экономическая интерпретация двойственной задачи

Исходная задача
Двойственная задача
m
g ( y ) bi yi min
n
f c x max
j j
j 1
n
a x b
ij j
i,
j 1
i 1
m
i 1,2,.., m
a
i 1
ij
yi c j
yi 0, i 1,2,..m.
x j 0, j 1,2,.., n
yi - цена за единицу i ресурса, b1 : b1 1
m
g
*
ст
m
*
bi y i g b1 1 y bi y *i g ст
y *1 f ст* y *1 f н*
*
i 1
*
н
*
1
i 2

7. Пример (распределение ресурсов)

f 3 x1 4 x2 max
Двойственная задача
g 9 y1 13 y2 y3 2 y4 min
(доход)
3 x1 2 x2 13 (сырье В )
y1 0 2 y1 3 y2 y3 3
y2 0 3 y1 2 y2 y3 y4 4
x1 x2 1 (спрос )
y 3 0
x2 2 (спрос)
y4 0
2 x1 3 x2 9 (сырье
x1 0
x2 0
А)

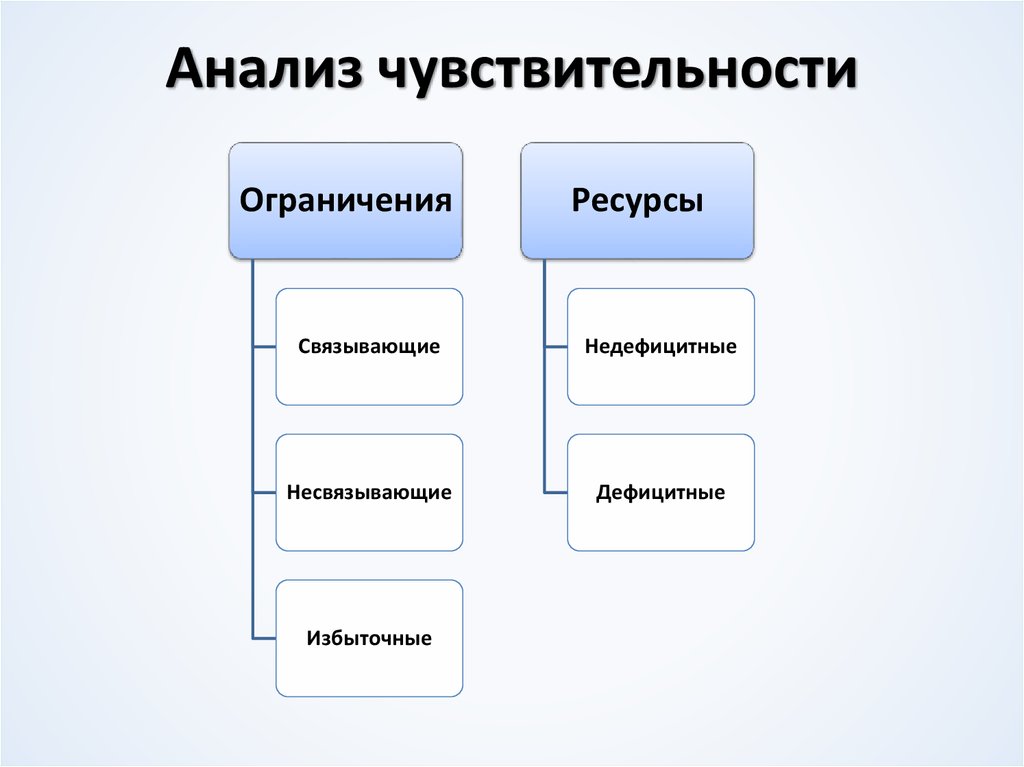
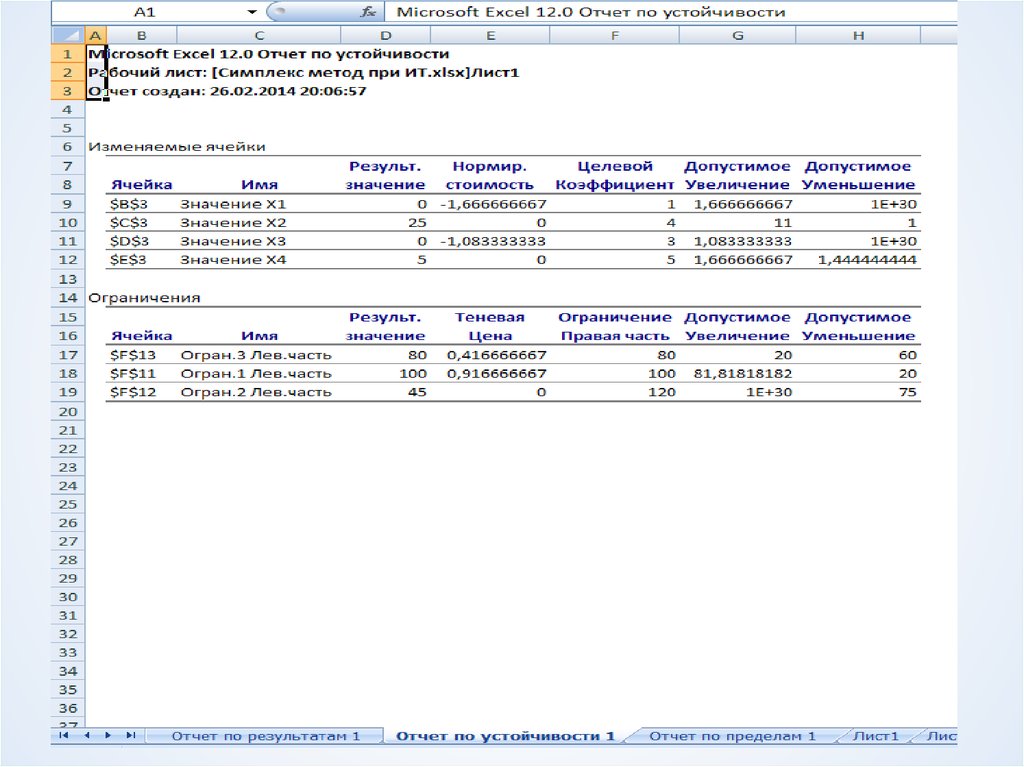
8. Анализ чувствительности

Ограничения
Ресурсы
Связывающие
Недефицитные
Несвязывающие
Дефицитные
Избыточные

9.

Анализ сокращения или увеличения ресурсов:
• на сколько можно увеличить (ограничения типа ≤) или уменьшить
(ограничения типа ≥) запас дефицитного ресурса для улучшения
оптимального значения ЦФ?
• на сколько можно уменьшить (ограничения типа ≤) или увеличить
(ограничения типа ≥) запас недефицитного ресурса при сохранении
полученного оптимального значения ЦФ?
Увеличение (уменьшение) запаса какого из ресурсов
наиболее выгодно?
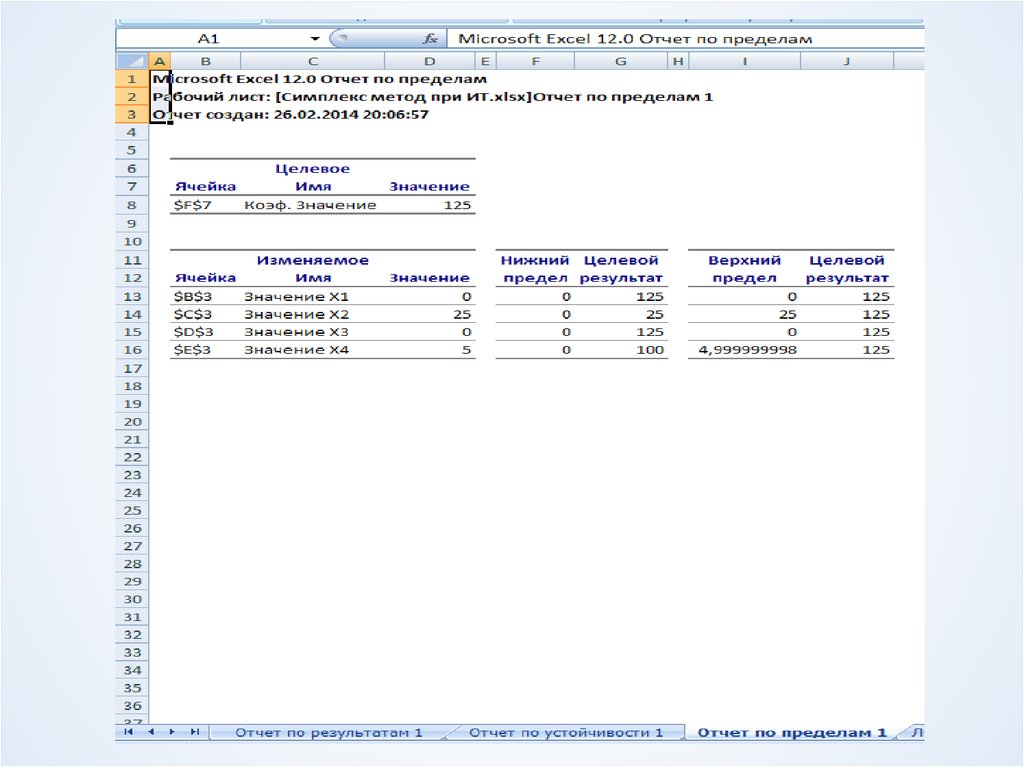
Анализ изменения целевых коэффициентов: каков
диапазон изменения коэффициентов ЦФ, при
котором не меняется оптимальное решение?

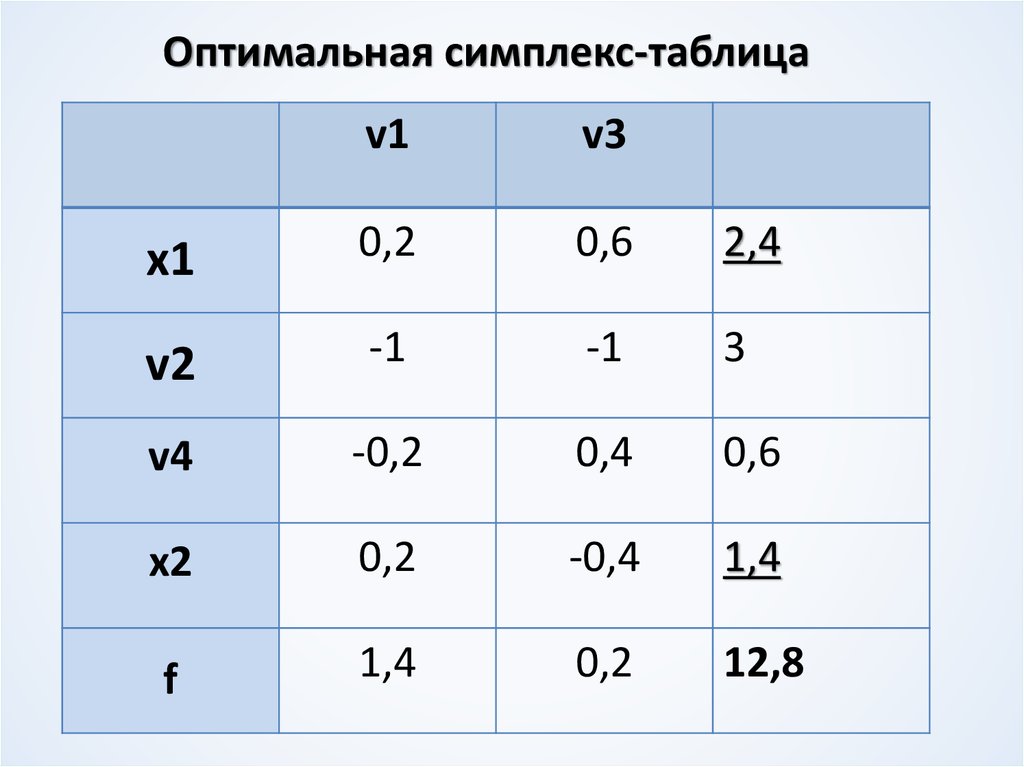
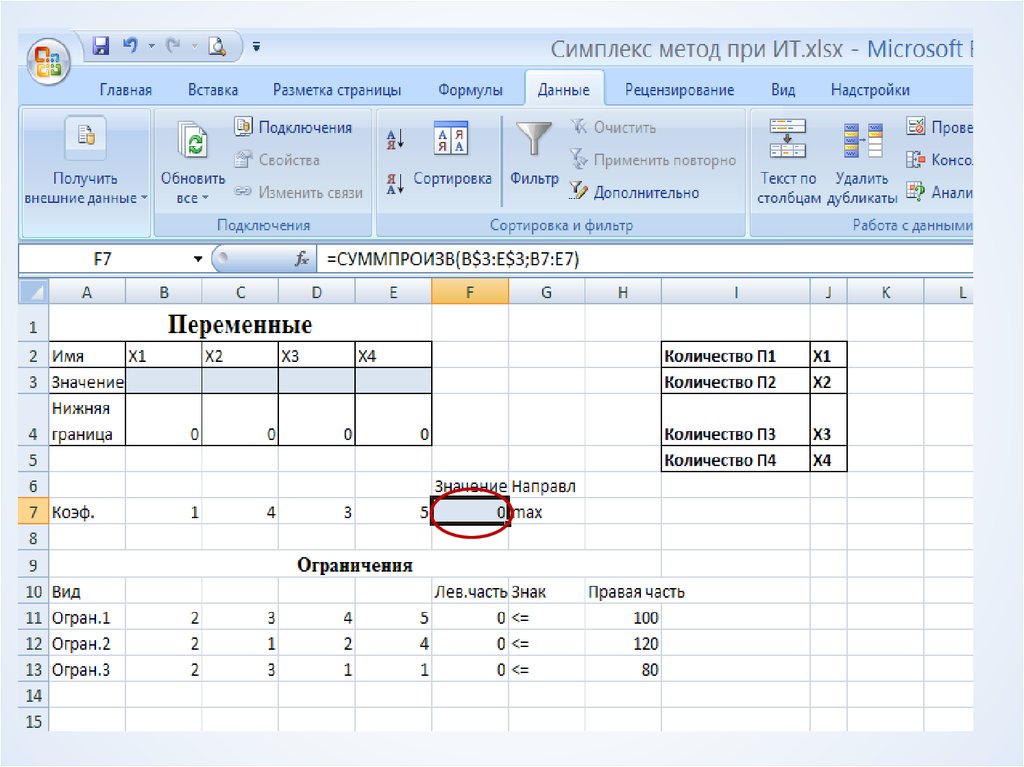
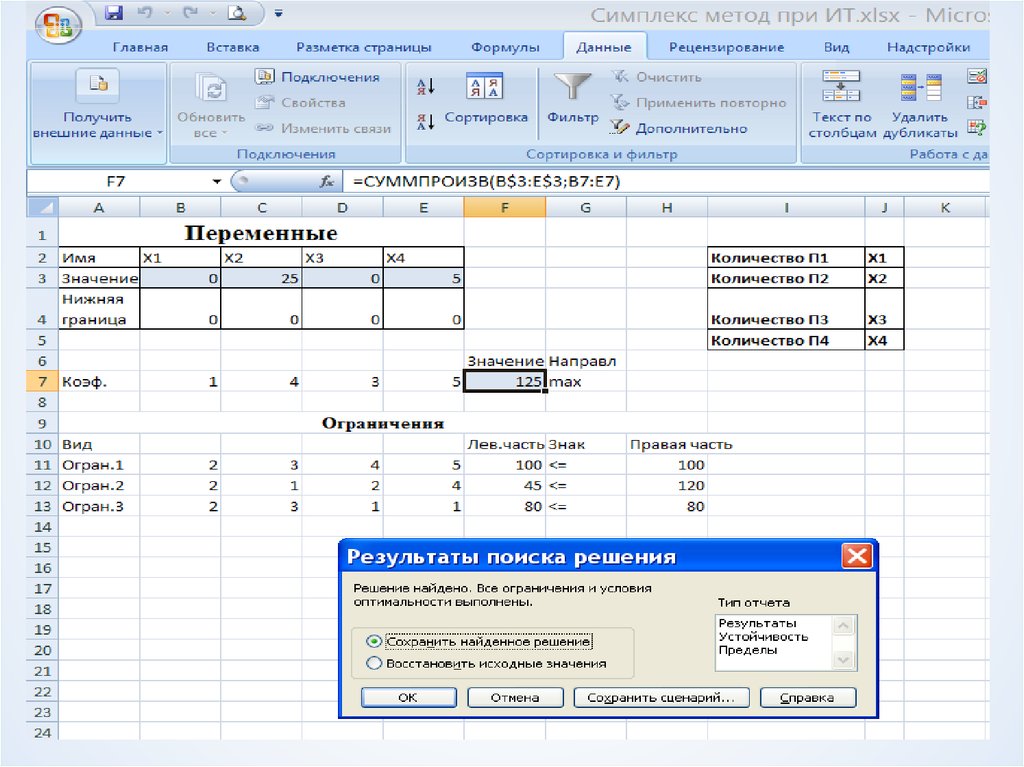
10. Оптимальная симплекс-таблица

v1
v3
х1
0,2
0,6
2,4
v2
-1
-1
3
v4
-0,2
0,4
0,6
х2
0,2
-0,4
1,4
f
1,4
0,2
12,8

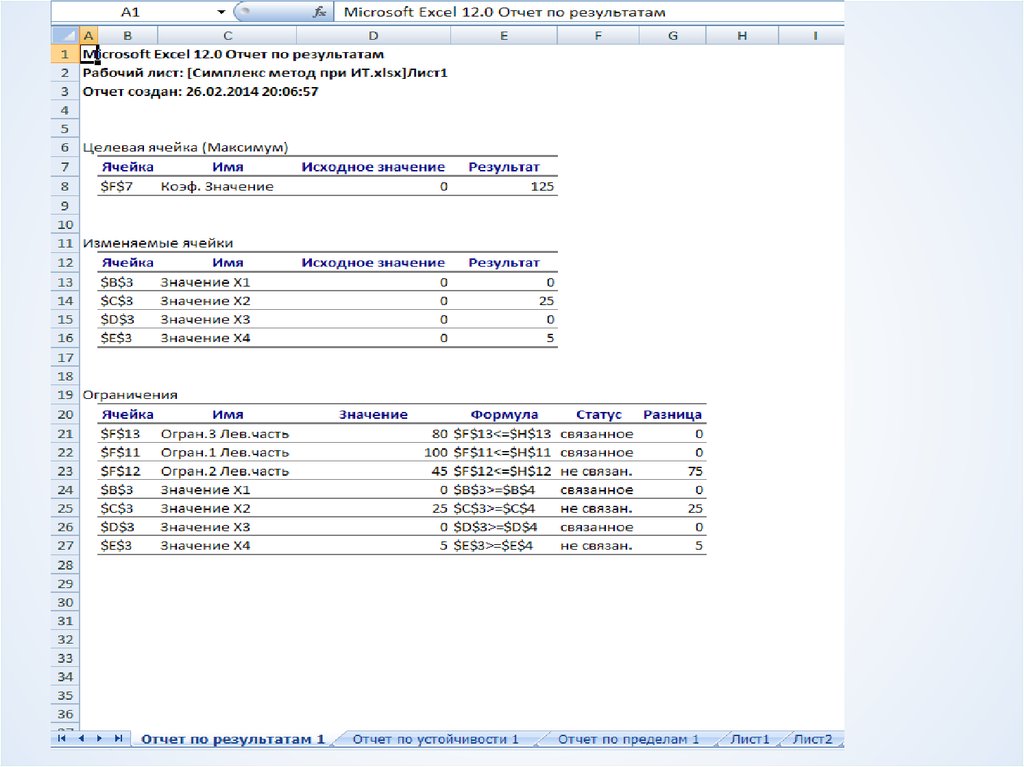
11. Оптимальное решение

f
*
max

12. Статус ресурсов

Слабая
переменная
v1
v2
v3
v4

13.

Пример.