Похожие презентации:
Различные способы решения иррациональных уравнений
1. Тема: Различные способы решения иррациональных уравнений
8 класс2. Работа устно
1. Дать определение квадратного корня изнеотрицательного числа?
2. Какие уравнения называются
иррациональными?
3. Как называют корень не удовлетворяющий
условию данного уравнения?
4. Какие способы решения иррационального
уравнения вам известно?
3. Какие из следующих уравнений являются иррациональными?
1) x x 22) x 2 x 1
3) x 2 x 3 1
2
4) x 2 1
3
4.
«Три пути ведут к знанию:путь размышления -это путь самый
благородный,
путь подражания- это путь самый
легкий,
и путь опыта- это путь самый горький»
Конфуций
5. «Найдите ошибки и заполните лист самоконтроля»
1)х 81
х 6561
2) х 3 27
х 3
3) х 4 16
х 2
4) 3 х 5
х 25
6. ответ
1) 65612) 3
3) Корней нет
4) 125
7. Является число корнем уравнения?
Является число x0корнем уравнения?
1) 5 х
х0 7
2) 5 х 2
3
х0 3
х 5
8. Основные способы решения иррационального уравнения
1. Использование свойстваПример:
х 5 2
a
n
n
a
1 этап. (технический)Возведем обе части данного уравнения в
квадрат:
х+5=4
Х=-1
2 этап. Проверка:
1 5 2
4 2
2 2
3 этап. Ответ:-1.
верно
9. Основные способы решения иррационального уравнения
2 способ: нахождение ОДЗПример:
х 5 2
1 этап. Нахождение ОДЗ: х 5 0
х 5
2 этап. Технический(возведение обеих частей
уравнения в квадрат, проверка с учетом
условия х 5 и запись ответа)
10. Уравнение вида
22 2 х х 1f ( x) g ( x)
g ( x) 0
f ( x) g ( x)
2
f ( x) g ( x)
11. Основные способы решения иррационального уравнения
3 способ. Переход к равносильной системе.22 2 х х 1
1 этап. На основании определения
арифметического корня данное уравнение
равносильно следующей системе:
х 1 0
2
22 2 х х 1
Х=3
Ответ: 3
х 1
2
22 2 х х 2 х 1
х 1
х 1
х 3
2
х 4 х 21 0 х 7
12. Уравнение вида
x 3 2x 7 ?f ( x) g ( x)
f ( x) 0
f ( x) g ( x) g ( x) 0
f ( x) g ( x)
13. Пример
x 3 2x 7x 3 0
2x 7 0
x 3 2x 7
х 3
х 3,5 х 4
х 4
14. Метод введения новой переменной
Пример: х 6 х 8 0Пусть х t , t 0 , тогда получим равносильное
уравнение: 2
t 6t 8 0
По теореме Виета найдем корни квадратного
уравнения:
t1 t2 6 t1 4
t t 8 t 2
1 2
2
Вернемся к замене переменной с учетом t 0
тогда : x 4 x1 16
x2 4
x 2
15. Проверочная работа
Решить уравнениеРешить уравнение
1) х 2 8 х
1) 2 х 1 8 х
2) х 7 х 12 0
2) х 3 х 18 0









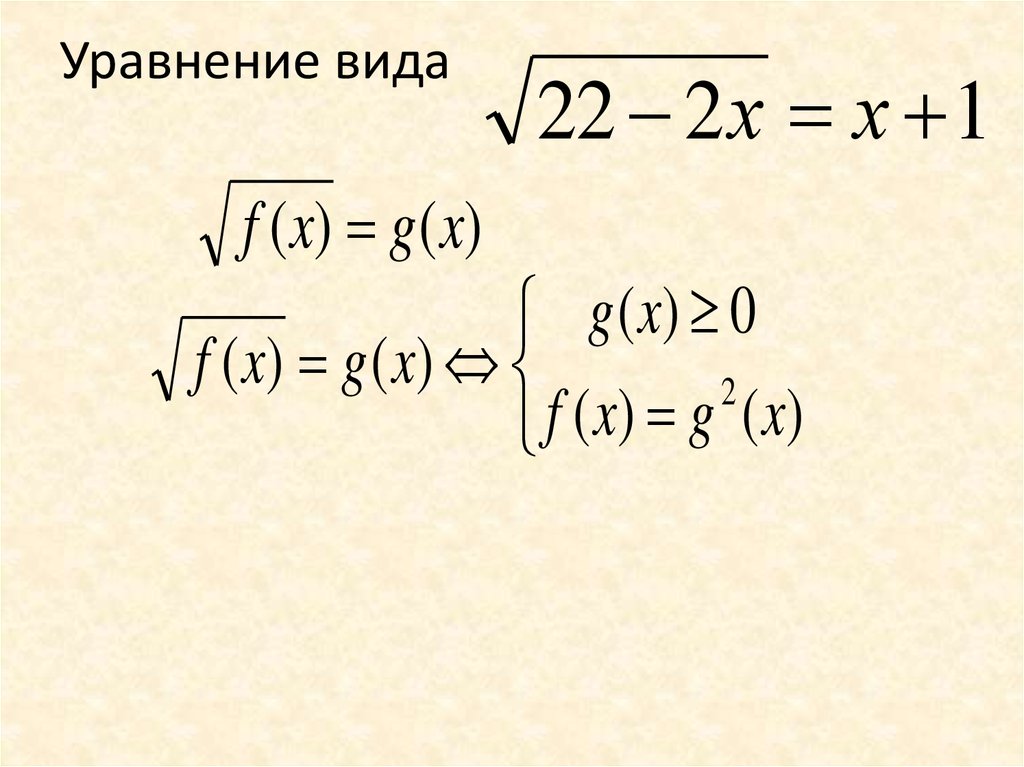

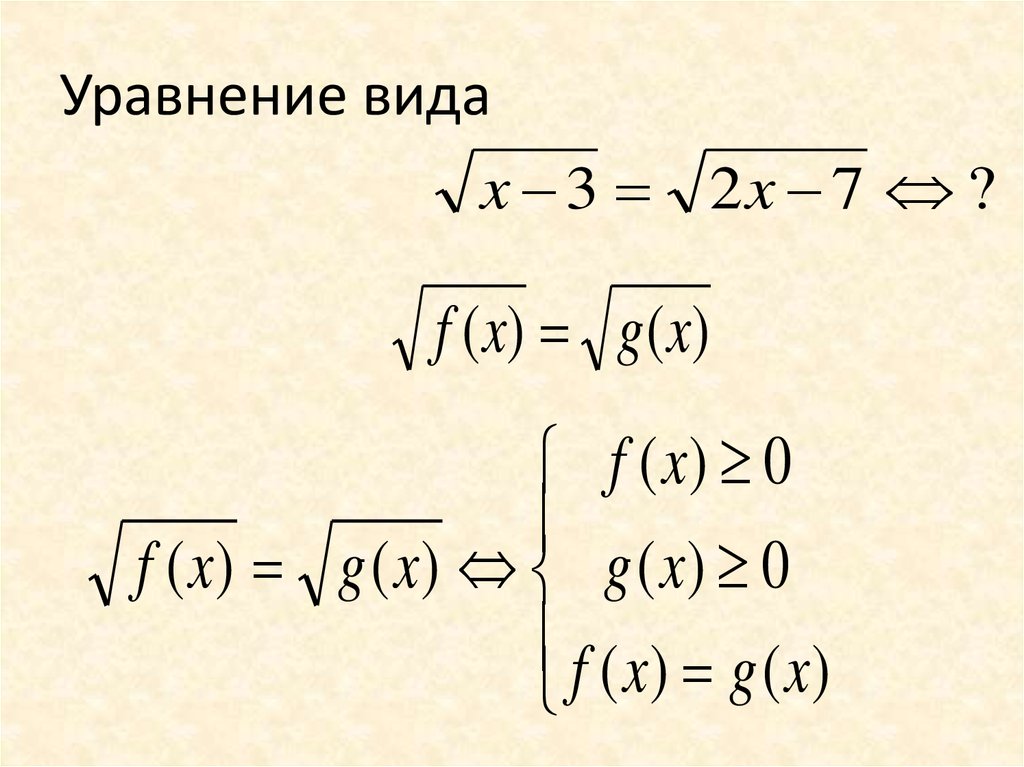
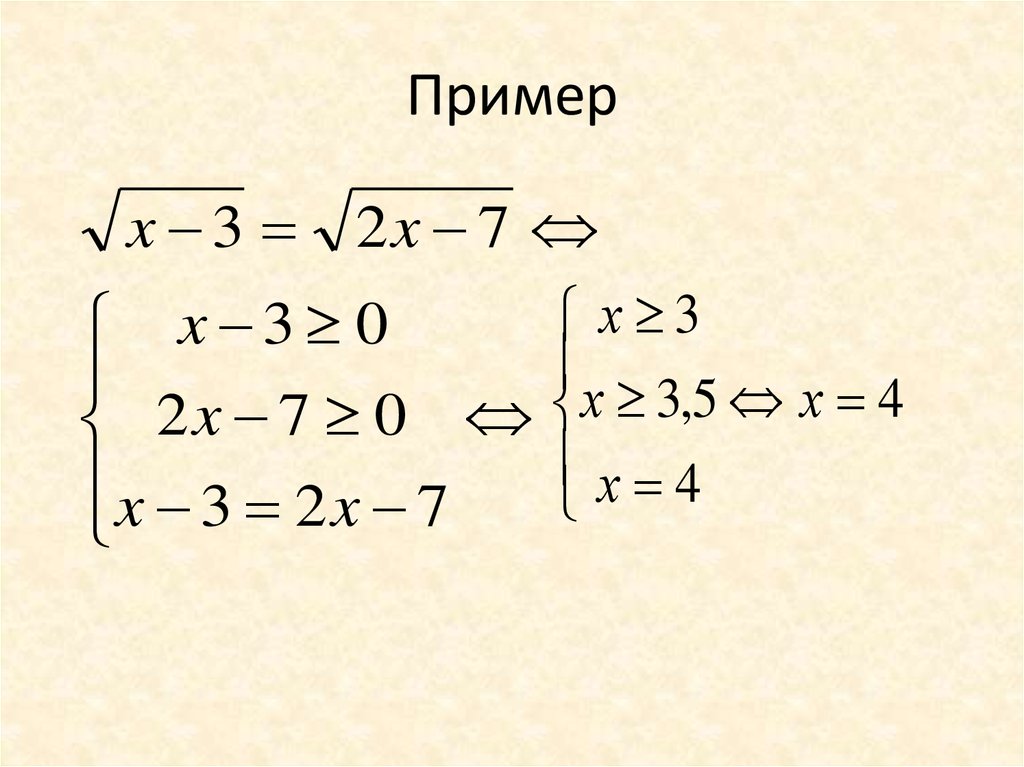



 Математика
Математика








