Похожие презентации:
Иррациональные уравнения и способы их решения
1. Иррациональные уравнения и способы их решения
2009-2010 уч. годВекслер Е. В.
ГОУ СОШ №252
Урок 1
Иррациональные
уравнения и
способы их решения
2. Какие уравнения называются ИРРАЦИОНАЛЬНЫМИ ?
Определение:Уравнения, в которых
переменная содержится
под знаком корня, называют
иррациональными.
3. Вспомните графики функций
4. Укажите, для каких значений переменных равенство верно.
xy x yx x
2
x x
4
2
x x 1
3
x x
5. Какие из предложенных уравнений не являются иррациональными?
6. Какие уравнения не имеют корней?
7. Какие уравнения из оставшихся можете решить?
8.
13
1
2
х
7
9
2 х 7 9
3
2 х 7 729
2 х 722
х 361
Ответ : 361
9.
11 ( х 6) 3 x 6 011
(
х
6
)
3
x
6
0
х 6 0
3х 6 0
х 6
Проверка
х 6 корень
Ответ : 2;6
х 2
3 6 6 0, значит
10.
44)) хх 22хх 44 22хх 1122
х 2х 4 2х 1
2
х 4х 3 0
2
х 3
х 1
Ответ : 1;3
11.
3 33 х 1 3 хх 11010
3х 1 х 3
х
10 3 3 х 1 х
3х 1 х 3
х 3
2
х 2 9х 8 0
3
х
1
х
6х 9
х 8
х 3
х 1
2
Проверка : 3 3 8 1 8 (верно) х 9 х 8 0
х 3
3 3 1 1 1 (неверно)
Ответ : 8
х 8
х 1
3х 1 х 2 6 х 9
Ответ : 8
12. Как предлагаете решить уравнение №9 ?
13.
Решить уравнение, исследуя область допустимыхзначений
1 х
2
4
5х 5 2
14. Как предлагаете решить уравнение № 14 ?
15. Свойства монотонности функций
f(x)=g(x)16. Свойства монотонности функций
f(x)=a17. Свойства монотонности функций
f(x)=a18. Свойства монотонности функций
•Если функция y=f(x) монотонная, тоуравнение f(x)=a имеет не более одного корня.
•Если функции y=f(x) и y=g(x) имеют разный
характер монотонности, то уравнение f(x)=g(x)
имеет не более одного корня.
19. Свойства монотонности функций
•Если функции y=f(x) и y=g(x) возрастают(убывают) на некотором множестве, то
функция y=f(x)+g(x) также возрастает
(убывает ) на этом множестве.
20.
•Функция видавозрастает при к>0 и убывает при к<0.
14 1 х 2 х 3 х 0
3
3
3
21. ВНИМАНИЕ !!!!!
•Если функции различной монотонности, томонотонность суммы, произведения, разности этих
функций определить нельзя!!
Например:
2х 3 4 х 2
2х 3 4 х 2
22. Решить уравнение с помощью свойств монотонности.
2 х х 3 9 х23. Как предлагаете решить уравнение № 12 ?
24.
у х 13
у x 1
2
Нет корней
12 х 1 x 1
3
2
25. Какими способами теперь можем решать иррациональные уравнения?
1.Возведение в степень.2.Уединение корня.
3.Исследование области допустимых
значений.
4.Графический способ
5.Использование свойств монотонности
26.
х 1 х 3 2Уединение корня
х 1 1 х
Исследование области
допустимых значений
х х 12
3
1
x 1 2
x
Графический способ
х 2х х х х
2
Возведение в степень
2
Использование
свойств
монотонности
27. Домашнее задание
§9 Иррациональные уравненияРешить уравнения на карточке
28.
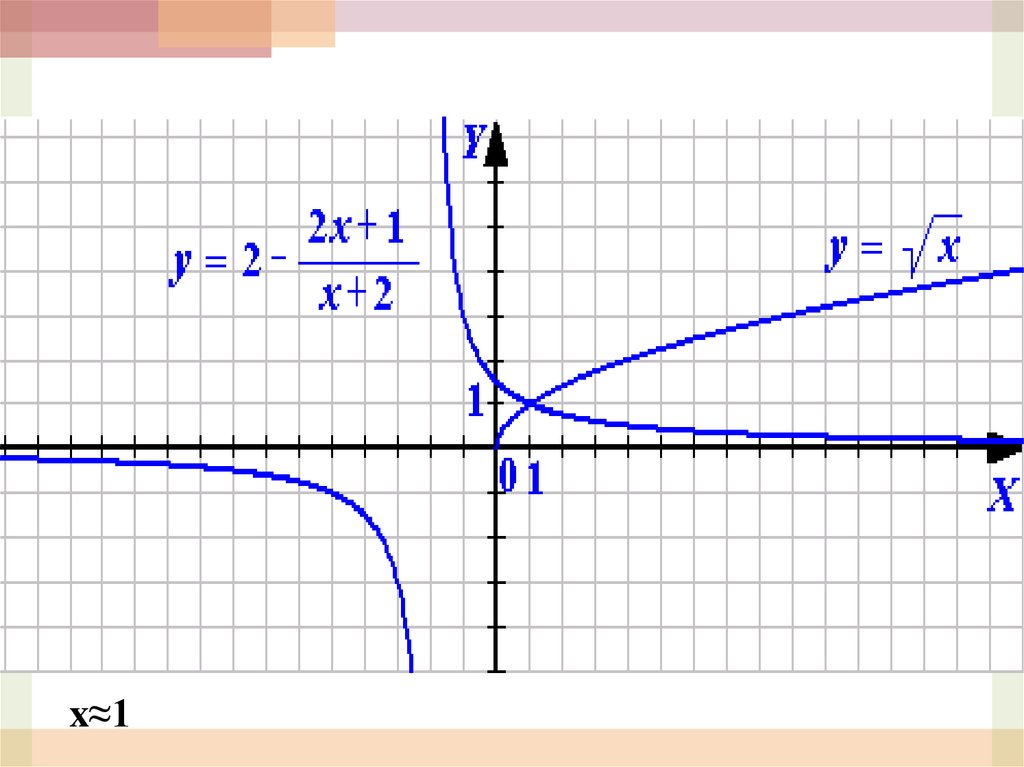
31
x 1 2
x
x ≈0,9
29.
Построим в одной и той же системе координат графикифункций:
D(y)=[0;+ ) График - кривая линия,
y(x)=
x
расположенная на промежутке [0;+ )
а)
3
g ( x)
б)
x 2
x
0
1 4 9 16
y
0
1 2 3
1
1
3
0,6
4
D(g)=(- ; - 2) (- 2; + )
Дробно-линейная функция, график – гипербола
x
y
-8 -7
- 0,5 - 0,6
-5
-1
-4
- 1,5
-3
-3
-1
3
0
1,5
4
0,5
30.
x≈131.
у 6у х
у х2 3
у 3 х 1
у 3 х
32.
1 3 2 х 7 99 х 10 3 х 2
2) 3 х 5 2
10 3 3х 1 х
3 2 х 3х 4
4) х 2 х 4 2 х 1
2
5 3 2 х 7 9
6 х 8 3 7 х
7 х х 5 1
8) х х
11 ( х 6) 3x 6 0
12 3 х 1 x 2 1
13 4 х 2 3х 2 0
14 3 1 х 3 2 х 3 3 х 0
33.
х 1 х 3 2Уединение корня
х 1 1 х
Исследование
области допустимых
значений
х х 12
3
1
x 1 2
x
Графический способ
х 2х х х х
2
Возведение в степень
2
Использование
свойств
монотонности







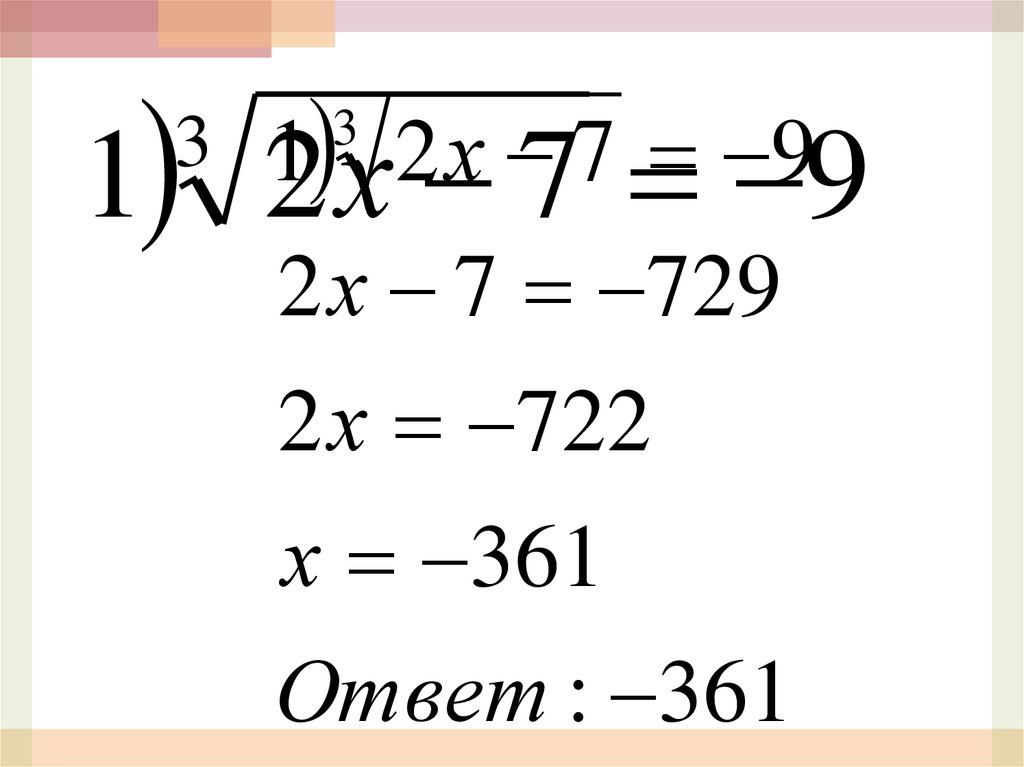

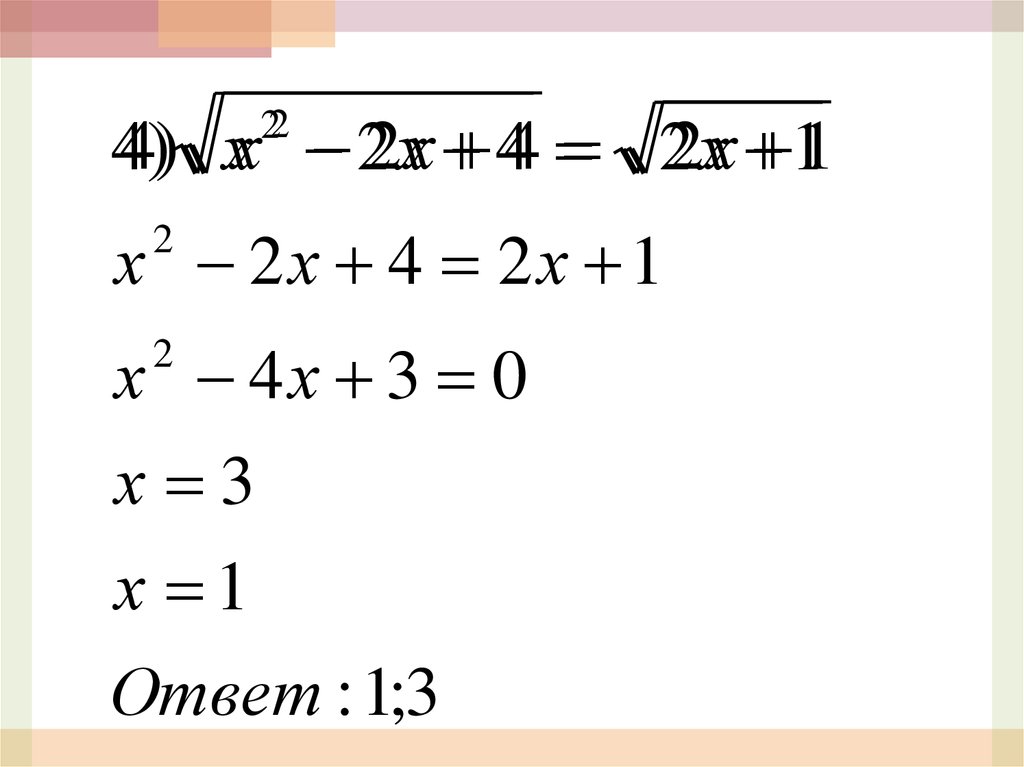





















 Математика
Математика








