Основная (каноническая) задача линейного программирования (ОЗЛП)

1. Основная (каноническая) задача линейного программирования (ОЗЛП)

Определить
,
(1)
где
,
;
(2)
;
.

2. Геометрический метод решения ОЗЛП.

В практических задачах, как правило
Предполагаем что
Выразим
,
.
.
m базисных переменных через две свободных
(например, x1 и
x2 ). Система уравнений (2) примет вид:
(3)

3.

С
учетом
условия
неотрицательности
переменных
множество G можно представить в виде системы
неравенств:
(4)
Отложим по осям ОХ1 и ОХ2 значения свободных
переменных,
а
также
построим
соответствующие неравенствам (4):
полуплоскости,

4.

5.

Утверждение. ОДР, если она существует, всегда является
выпуклым множеством, имеющим форму многоугольника.
Поиск оптимального решения.
Подставим соотношение (3) в (1).
Получим:
.
(5)
Будем рассматривать целевую функцию в виде:
,
(6)
т.к. параметр a не влияет на оптимальное решение x opt .

6.

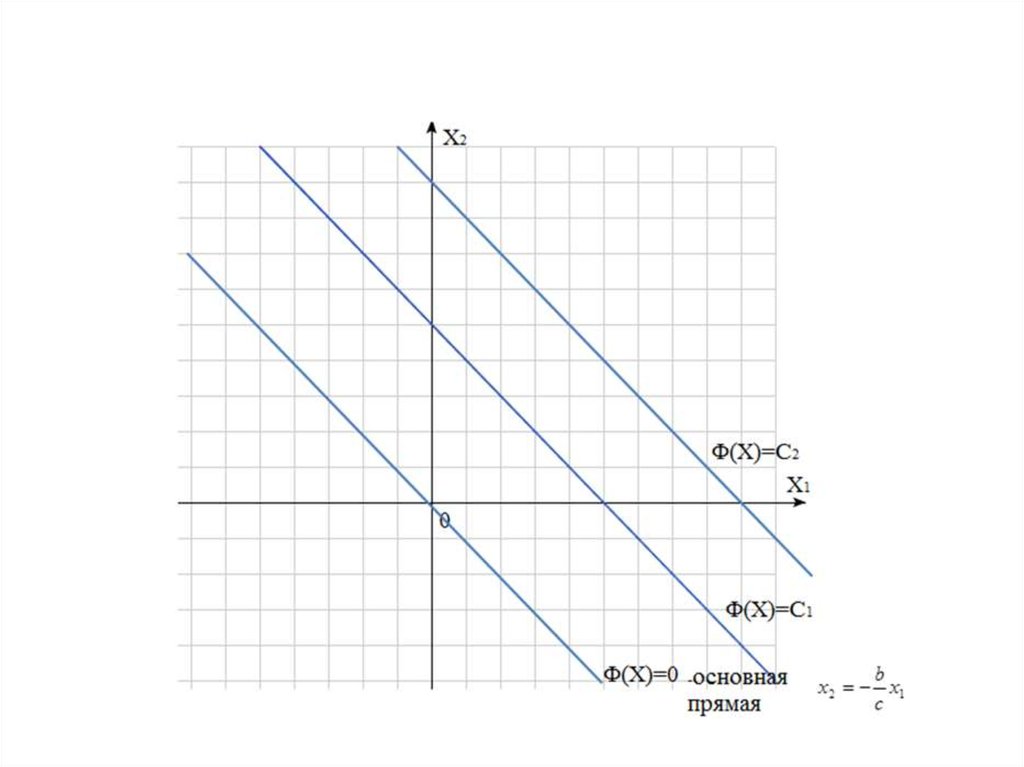
Линии уровня целевой функции
Ф x
- параллельные
прямые:
Ф x C1
Ф x C2
Изменение
параметра
перемещению прямой
В
каком
прямую
Ф x Cn
C
Ф x 0
направлении
Ф x 0
равносильно
Ф x 0,
мысленному
параллельно самой себе.
необходимо
, чтобы значение Ф
перемещать
x убывало?

7.

8.

9.

10.

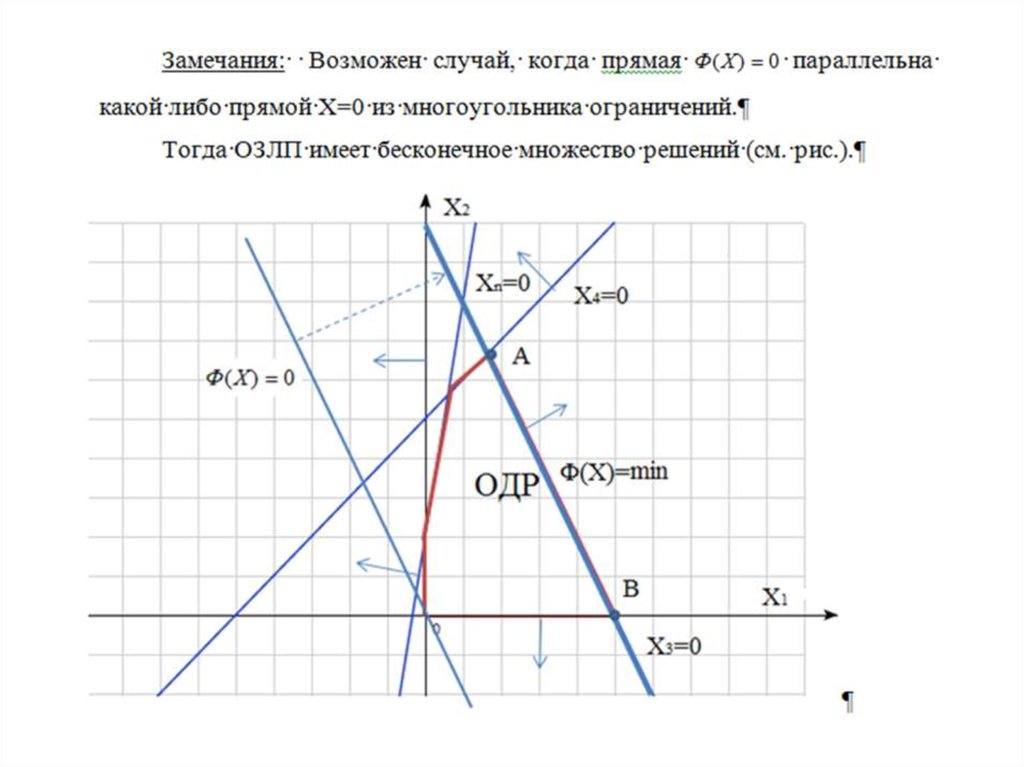
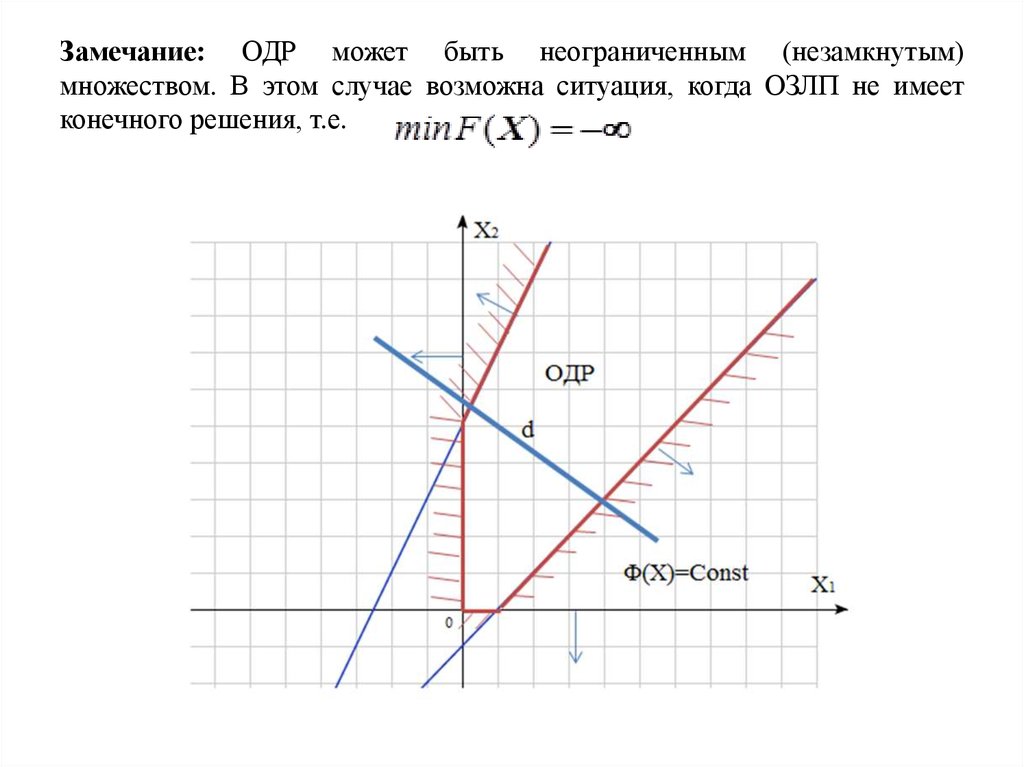
11. Замечание: ОДР может быть неограниченным (незамкнутым) множеством. В этом случае возможна ситуация, когда ОЗЛП не имеет

конечного решения, т.е.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

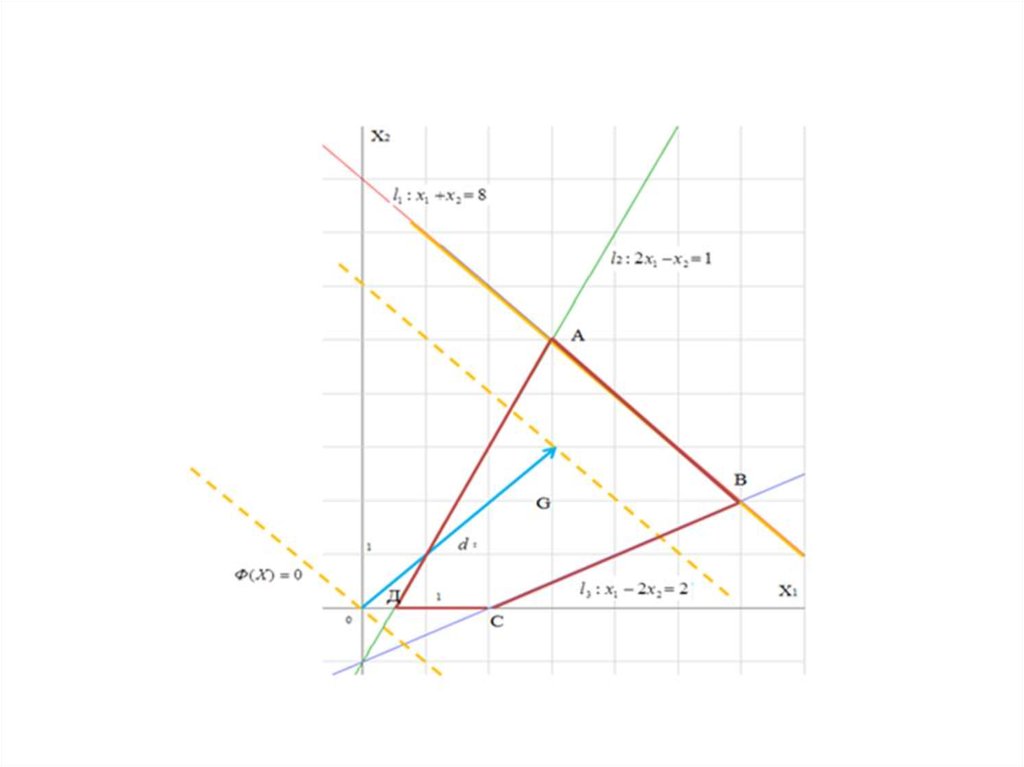
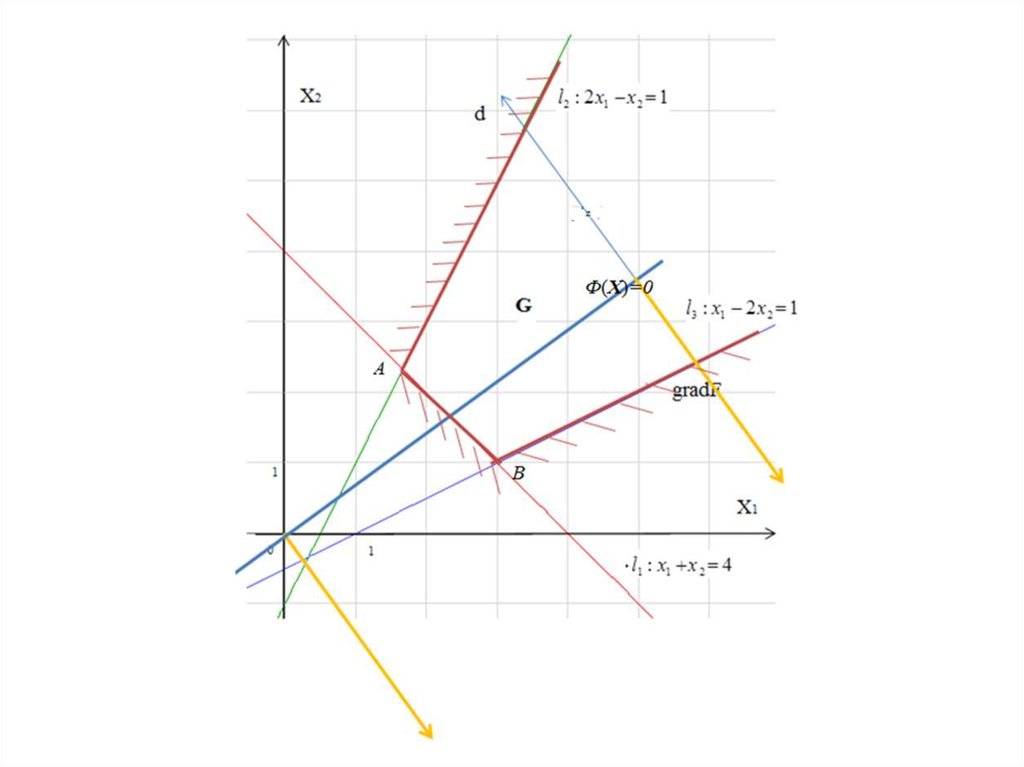
22. Задача 3.

Определить
при ограничениях:
Решение.
.
основные переменные;
свободные переменные .

23.

Выразим основные переменные через свободные:
;
.

24.

Оптимальное решение достигается в точке А(0; 0).
Значения переменных:
;
;
.