Формулы сокращенного умножения

1.

Формулы сокращенного умножения
1) Квадрат суммы.
2) Квадрат разности.
3) Разность квадратов.
4) Куб суммы.
5) Куб разности.
6) Сумма кубов.
7) Разность кубов.
8) Треугольник Паскаля.
9) Бином Ньютона.

2.

(a b) a 2ab b
2
2
Квадрат суммы двух чисел равен:
квадрату первого числа,
плюс удвоенное произведение
первого числа на второе,
плюс квадрат второго числа.
(
=
+
+2
2
) =
+
2

3.

Например:
1). m n
m 2mn n
2). 1 p
1 2 p p
3). 2m 5n
4m 20mn 25n
2
2
2
2
4). 3 x 4 y
2
2 2
3 2
2
3
5 2
2
2
9 x 24 xy 16 y
6) 3ab 2c
7). p q
5). a b
2
2
2
a 2a b b
4
2
2
2
2
4
9a b 12ab c 4c
2
4
2 3
p 2p q q
6
3
5
10
6

4.

(a b) a 2ab b
2
2
2
Квадрат разности двух чисел равен:
квадрату первого числа,
минус удвоенное произведение
первого числа на второе,
плюс квадрат второго числа.
Формула шутка
(
=
- ) =
-2
+
2

5.

6.

a b a b a b
2
2
Разность квадратов двух чисел равна:
произведению
разности этих чисел на их сумму.
Формула шутка
2
=(
-
2
=
.
- )( + )

7.

Например:
y x y x
2
2). 9 3m 3 3m 3 3m
1). y x
2
2
3). 16 p
4
4). 25 a
6
5). m n
4
2
6). 1 x
4
7). p 49
8
4 p 4 p
5 a 5 a
m n m n
1 x 1 x
p 7 p 7
2
2
3
2
3
2
2
4
2
4

8.

( a b)
3
a 3a b 3ab b
3
2
2
Куб суммы двух чисел равен
кубу первого числа плюс утроенное
произведение квадрата первого
числа на второе, плюс утроенное
произведение первого
числа на квадрат второго числа, плюс
куб второго числа.
3

9.

Например:
1). x y
3
x 3 x y 3 xy y
3
2
2
3
2). a 2 a 3 6a 2 12a 8
3
3). 2a 3b 8a 3 3 4a 2 3b 3 2a 9b 2 27b 3
3
4). m 4 m 3 3 m 2 4 3 m 16 64
3
5). x 3 z x 3 x 3 z 3 x 9 z 27 z
3
3
2
2
6). 2b 3 8b 3 4b 3 3 2b 9 27
3
3
2
7). n 1 n 3n 3n 1
2
3
6
4
2
3

10.

( a b)
3
a 3a b 3ab b
3
2
2
3
Куб разности двух чисел равен
кубу первого числа минус утроенное
произведение квадрата первого
числа на второе плюс утроенное
произведение первого
числа на квадрат второго числа минус куб
второго числа.

11.

Например:
1). x y
3
x 3 x y 3 xy y
3
2
2
3
2). a 2 a 3 6a 2 12a 8
3
3). 2a 3b 8a 3 3 4a 2 3b 3 2a 9b 2 27b 3
3
4). m 4 m 3 3 m 2 4 3 m 16 64
3
5). x 3 z x 3 3 x 2 3 z 3 x 9 z 2 27 z 3
3
6). 2b 3 8b 3 3 4b 2 3 3 2b 9 27
3
3
7). n 1 n 3n 3n 1
2
6
4
2

12.

a b
3
3
a b a ab b
2
2
Сумма кубов равна
произведению суммы этих чисел
на неполный квадрат их разности.

13.

Например:
1).m n
3
3
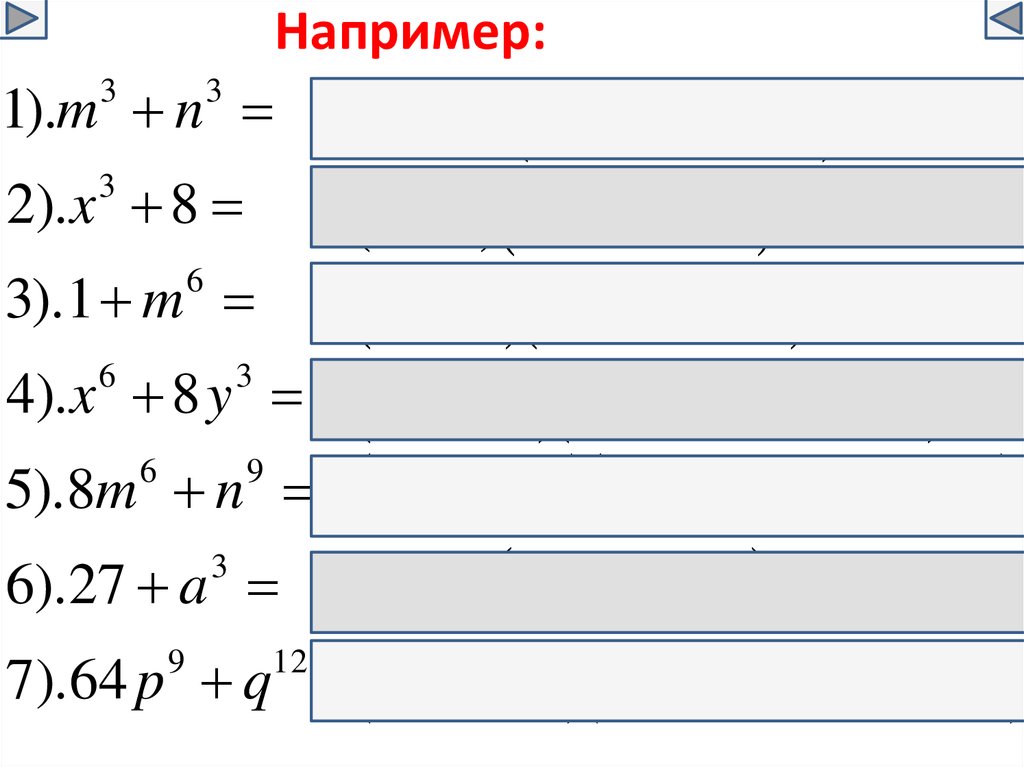
2).x 8
3
m n m mn n
2
x 2 x 2 x 4
2
2
1 m 1 m m
4).x 8 y x 2 y x 2 x y 4 y
5).8m n 2m n 4m 2m n n
6).27 a 3 a 9 3a a
7).64 p q 4 p q 16 p 4 p q q
3).1 m
6
6
2
3
6
2
2
9
4
4
2
3
2
4
3
9
2
2
3
6
3
4
8
2
12
3
4
6

14.

a b
3
3
a b a ab b
2
2
Разность кубов равна
произведению разности этих чисел
на неполный квадрат их суммы.

15.

Например:
1).m n
3
3
2).x 8
3
m n m mn n
2
x 2 x 2 x 4
2
2
1 m 1 m m
4).x 8 y x 2 y x 2 x y 4 y
5).8m n 2m n 4m 2m n n
3 a 9 3a a
6).27 a
7).64 p q 4 p q 16 p 4 p q q
3).1 m
6
6
2
3
6
2
2
9
4
4
2
3
2
4
3
9
2
2
3
6
3
4
8
2
12
3
4
6

16.

Треугольник Паскаля.
Степень
двучлена
Коэффициенты
a b
1
a b
0
a b
2
1
1 1
1 2 1
a b
1 3 3 1
a b
1 4 6 4 1
3
4
a b
5
1 5 10 10 5 1
6
1 6 15 20 15 6 1
a b

17.

Бином Ньютона.
a b
n
1 n 1
n
2 n 2 2
n
n 1
n
a C a b C a b ... C ab
n
n 1
b
n!
n n 1 ... n k 1
C
n k !k!
k!
k
n
n

English Русский Правила