Похожие презентации:
Теория вероятностей и математическая статистика
1. Теория вероятностей и МАТЕМАТИЧЕСКая СТАТИсТИКа практикум
ТЕОРИЯ ВЕРОЯТНОСТЕЙ ИМАТЕМАТИЧЕСКАЯ
СТАТИСТИКА
ПРАКТИКУМ
Мацкевич И.Ю.
Петрова Н.П.
Тарусина Л.И.
2.
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯСТАТИСТИКА
Практикум
для учащихся средних специальных заведений
Рекомендовано к изданию экспертным советом
Республиканского института профессионального образования
АВТОРЫ:
Мацкевич Ирина Юрьевна, ст. преподаватель Института информационных технологий
БГУИР,
Петрова Наталья Павловна, преподаватель Минского радиотехнического колледжа,
Тарусина Лилия Ивановна, преподаватель Минского радиотехнического колледжа
РЕЦЕНЗЕНТ:
Майсеня Людмила Иосифовна, зав. кафедрой физико-математических дисциплин ИИТ
БГУИР, д-р пед. наук, канд. физ.-мат. наук, доцент
3.
Оглавление• Предисловие
• Лабораторно-практическая работа 1
Классическое, геометрическое и статистическое определения вероятностей
событий
• Лабораторно-практическая работа 2
Теоремы сложения и умножения вероятностей независимых событий
• Лабораторно-практическая работа 3
Условная вероятность. Формула полной вероятности и формулы Байеса
• Лабораторно-практическая работа 4
Дискретные случайные величины. Биномиальный закон распределения
• Лабораторно-практическая работа 5
Повторение независимых испытаний
• Лабораторно-практическая работа 6
Непрерывные случайные величины
• Лабораторно-практическая работа 7
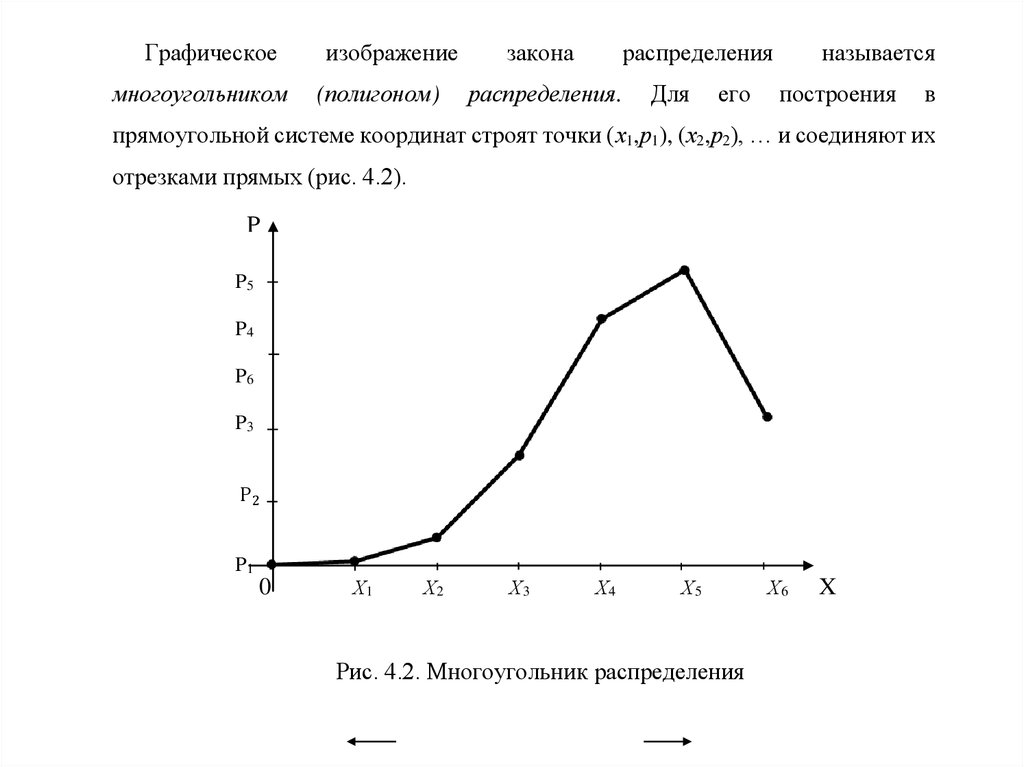
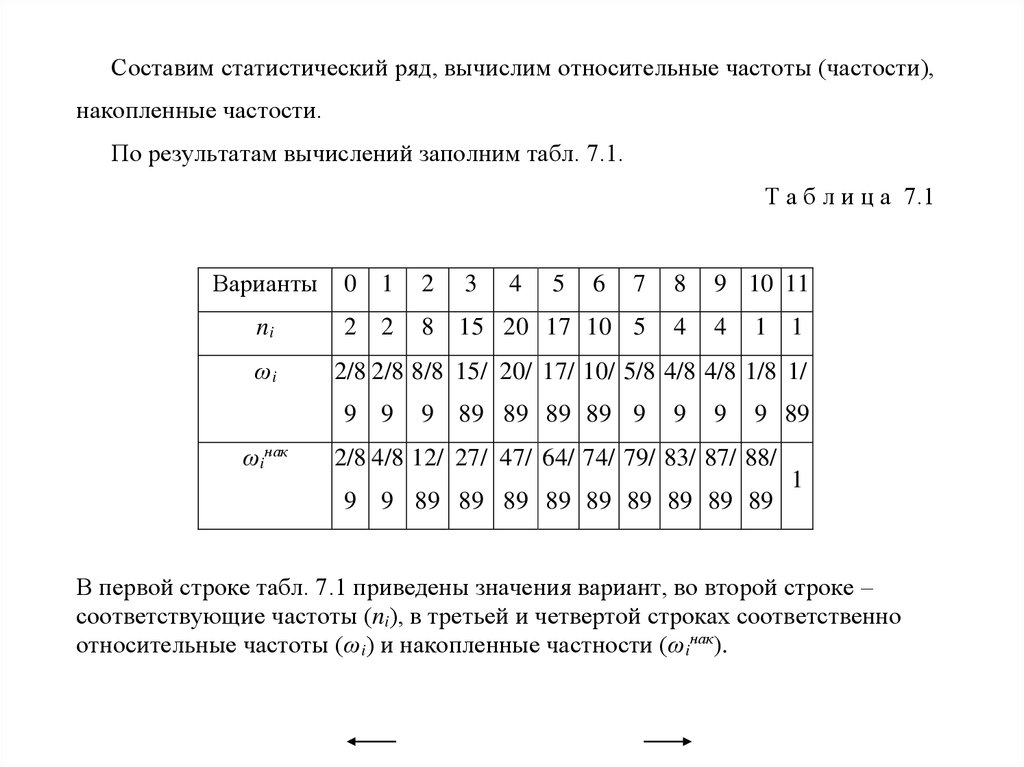
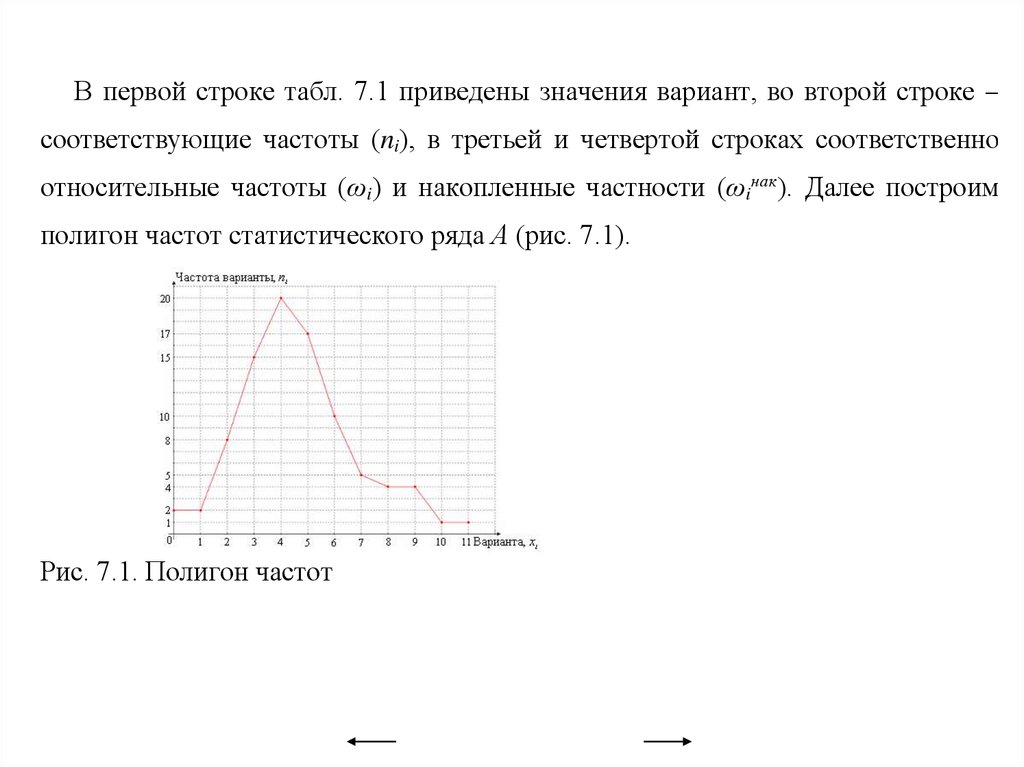
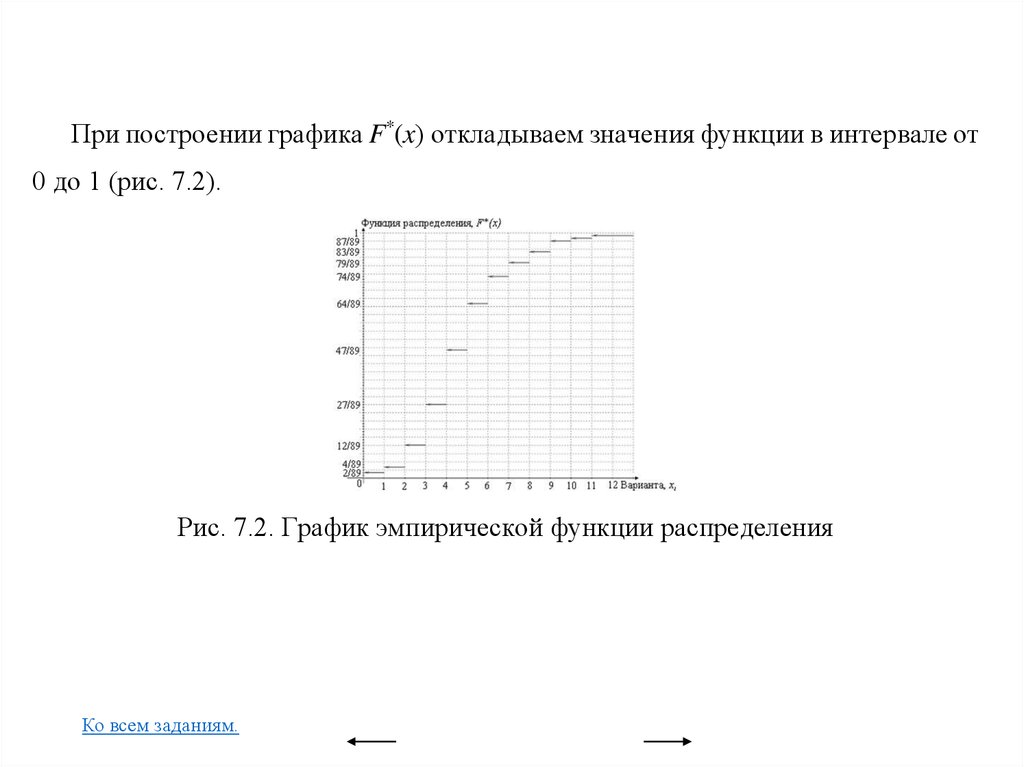
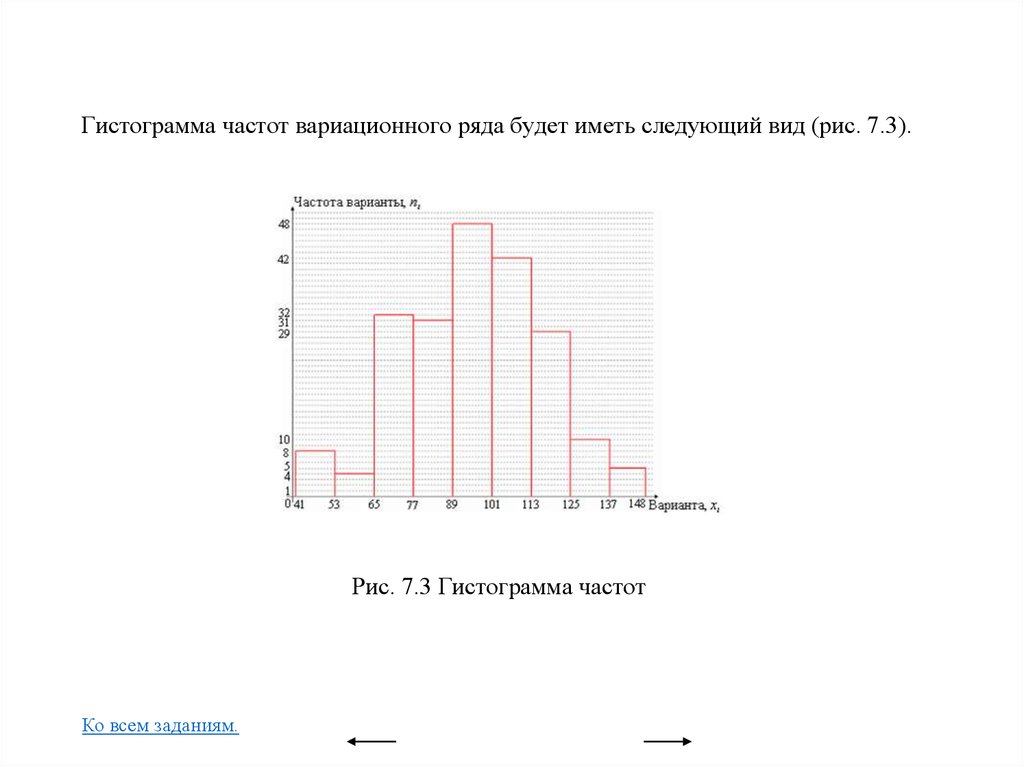
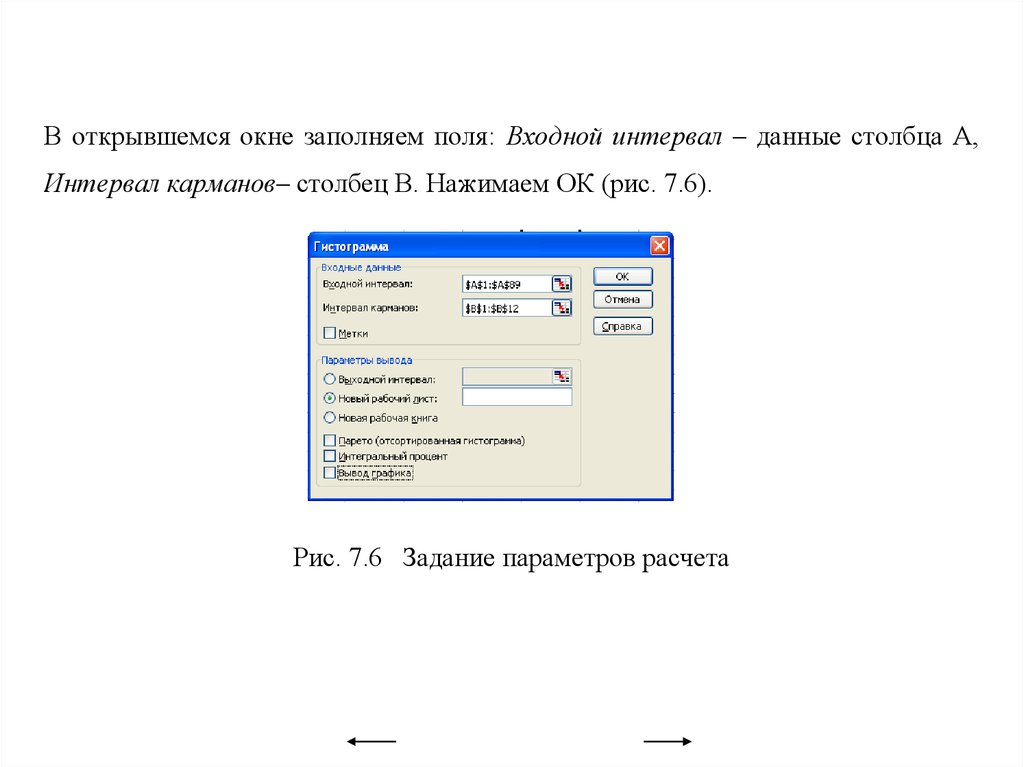
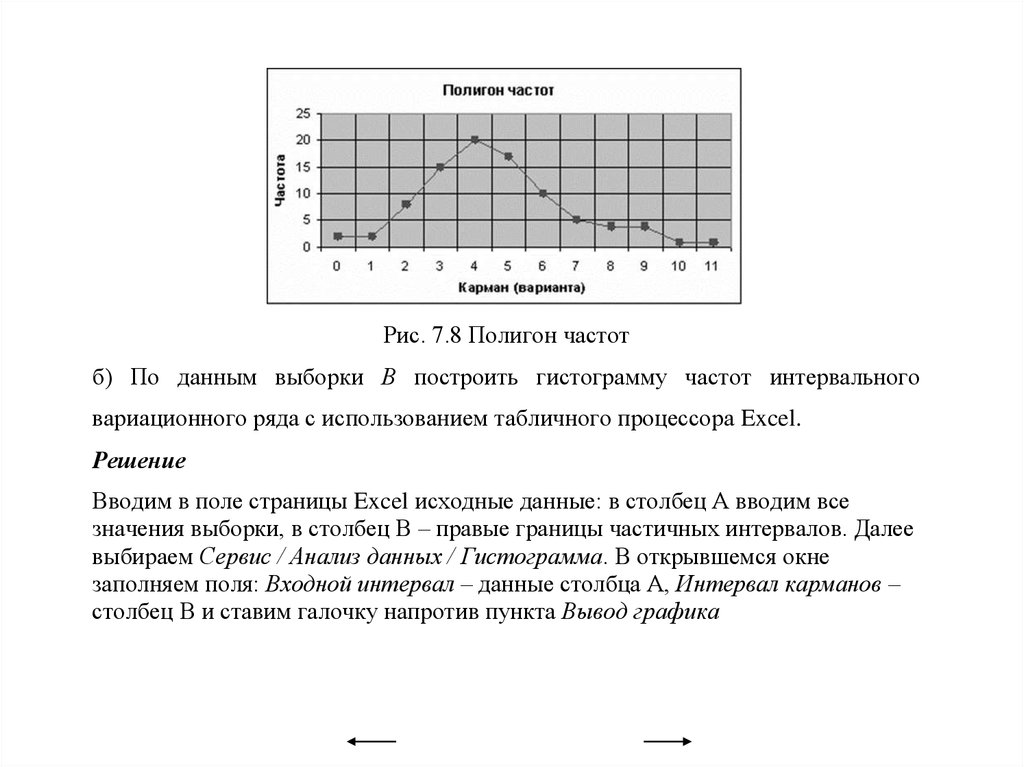
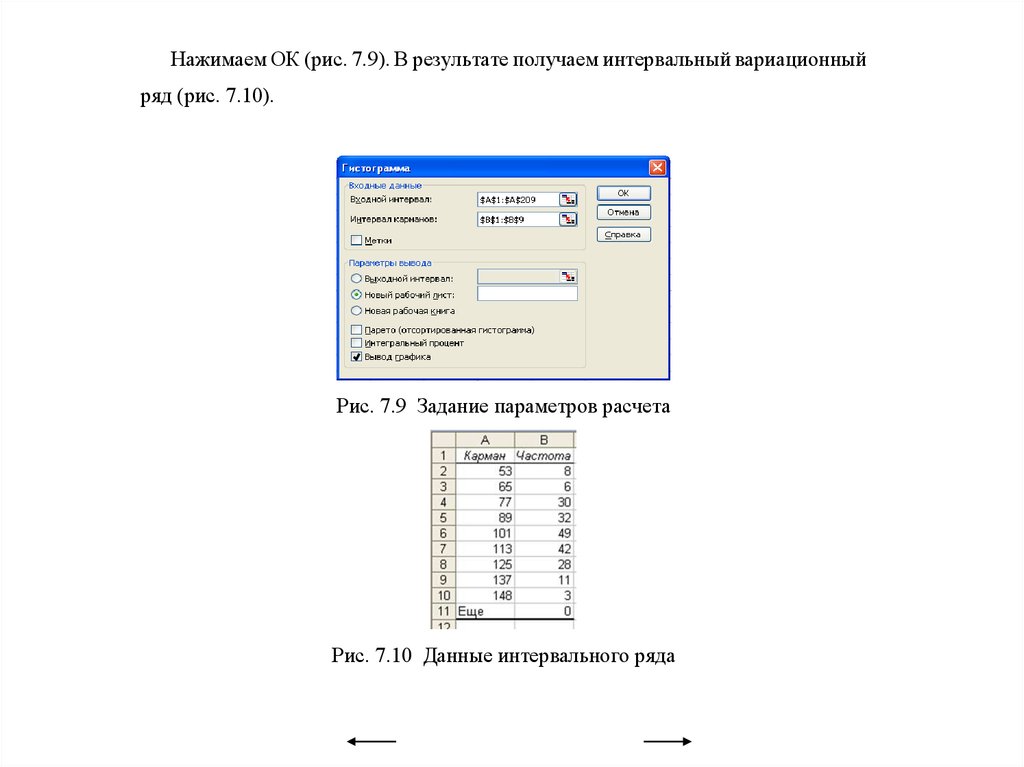
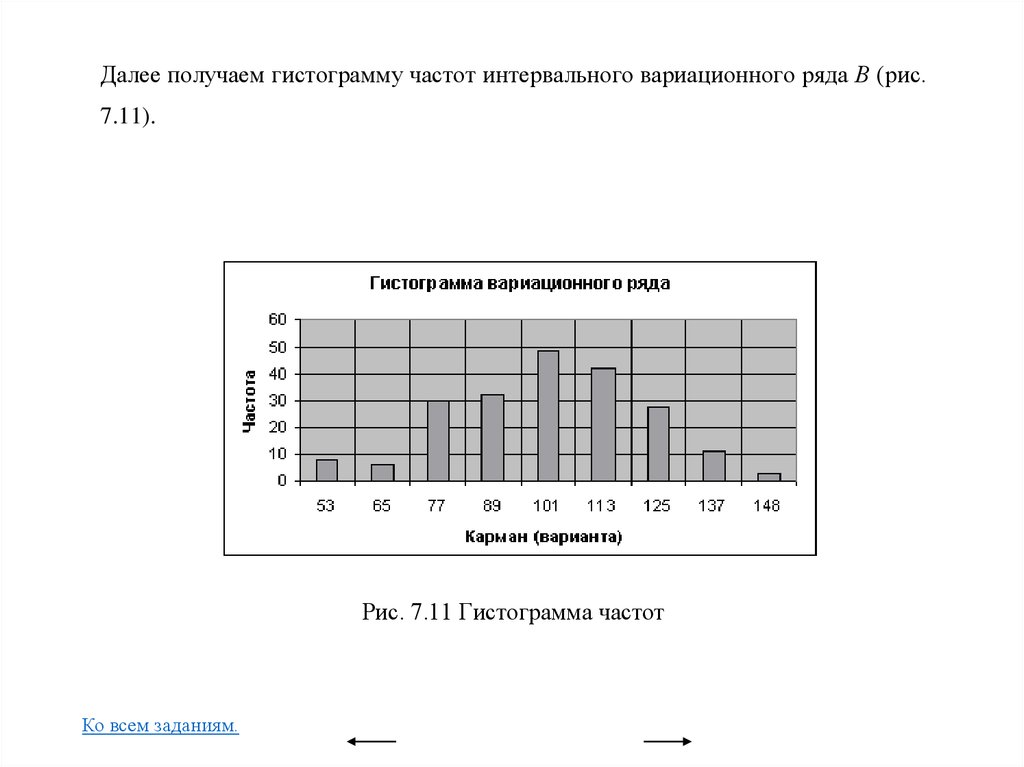
Вариационные ряды и их графическое изображение
• Лабораторно-практическая работа 8
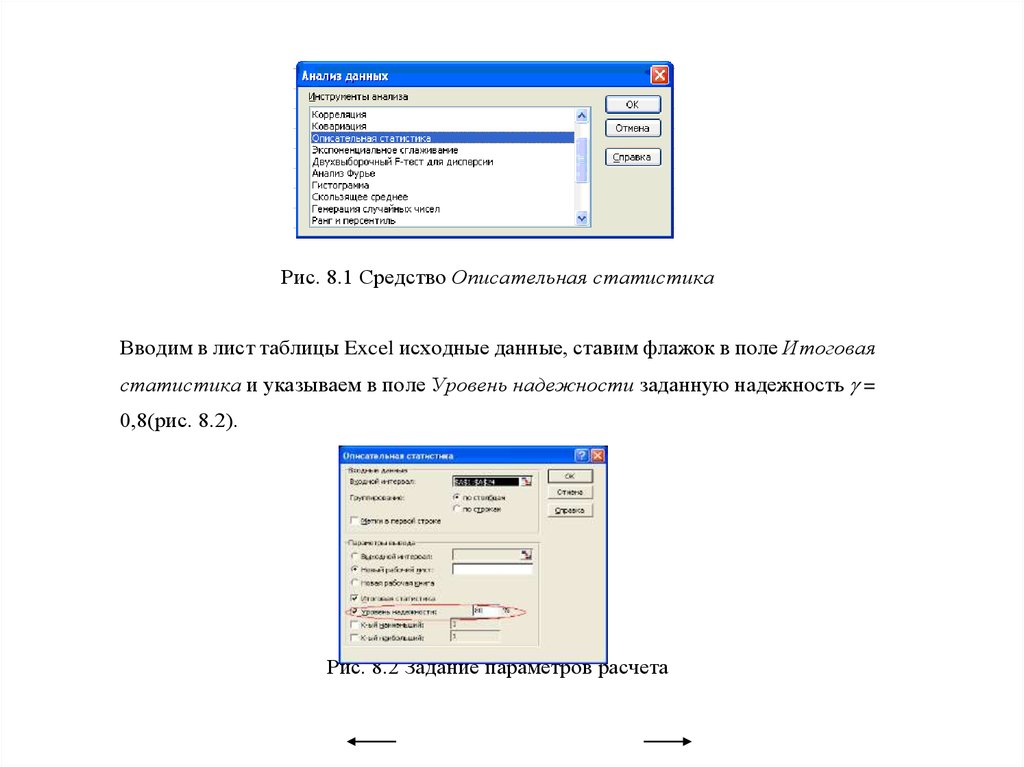
Точечные и интервальные оценки параметров распределения
4.
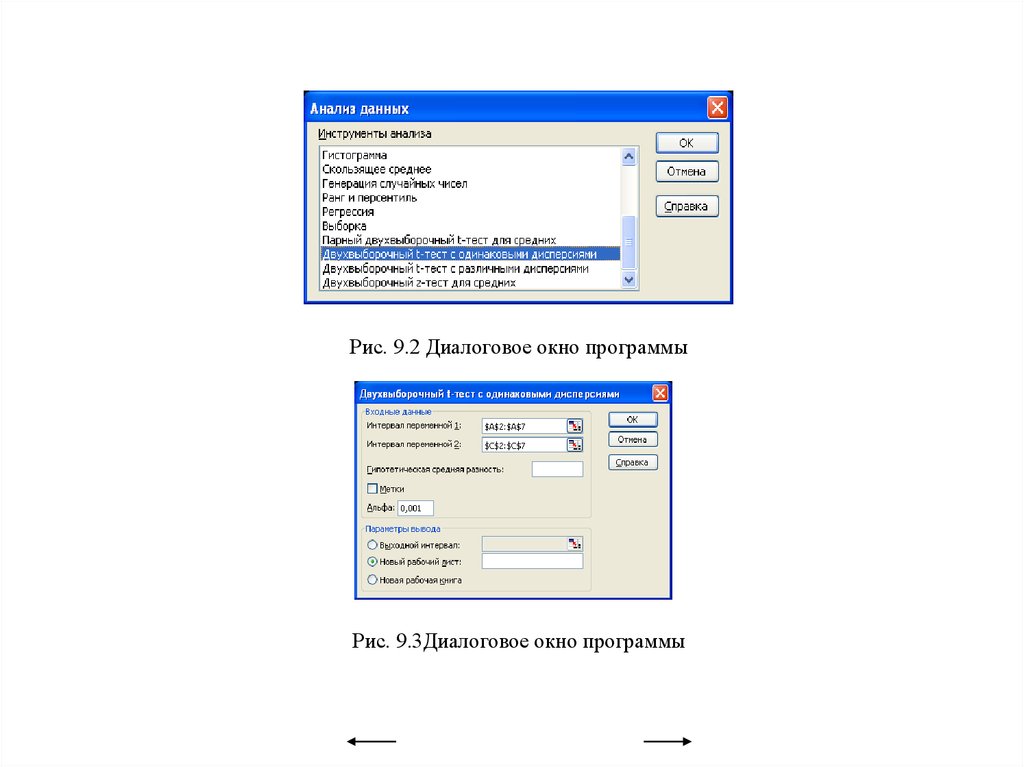
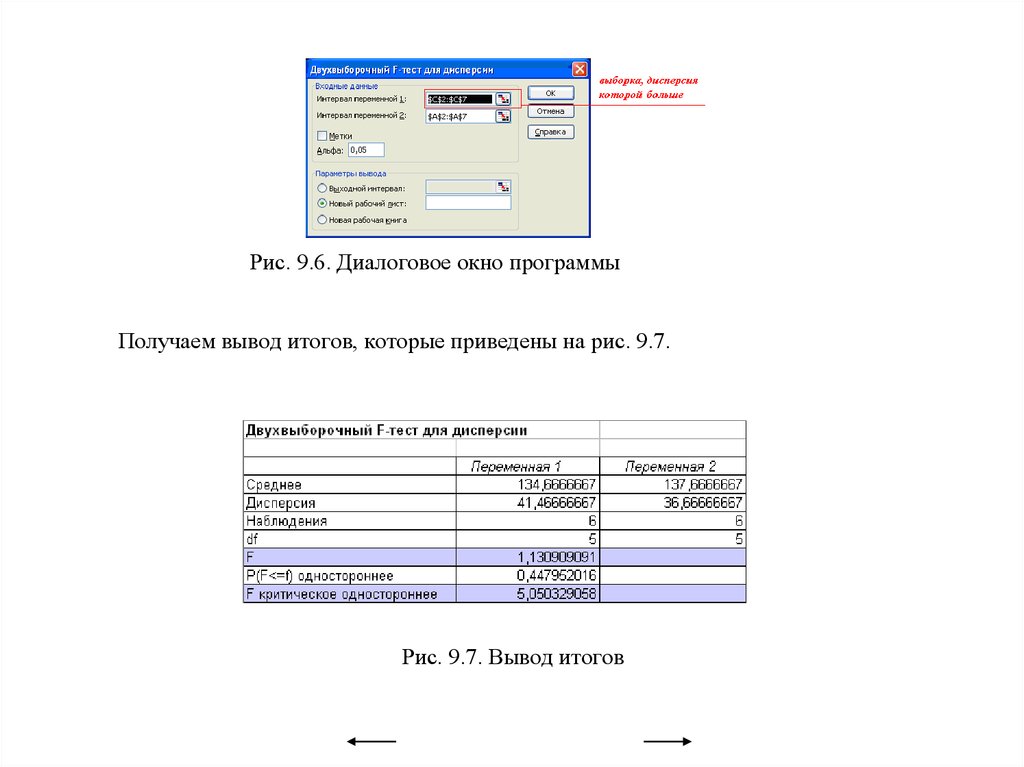
• Лабораторно-практическая работа 9Проверка параметрических гипотез
• Лабораторно-практическая работа 10
Проверка непараметрических гипотез
• Рекомендуемая литература
• Приложение 1
Выборки для задач математической статистики
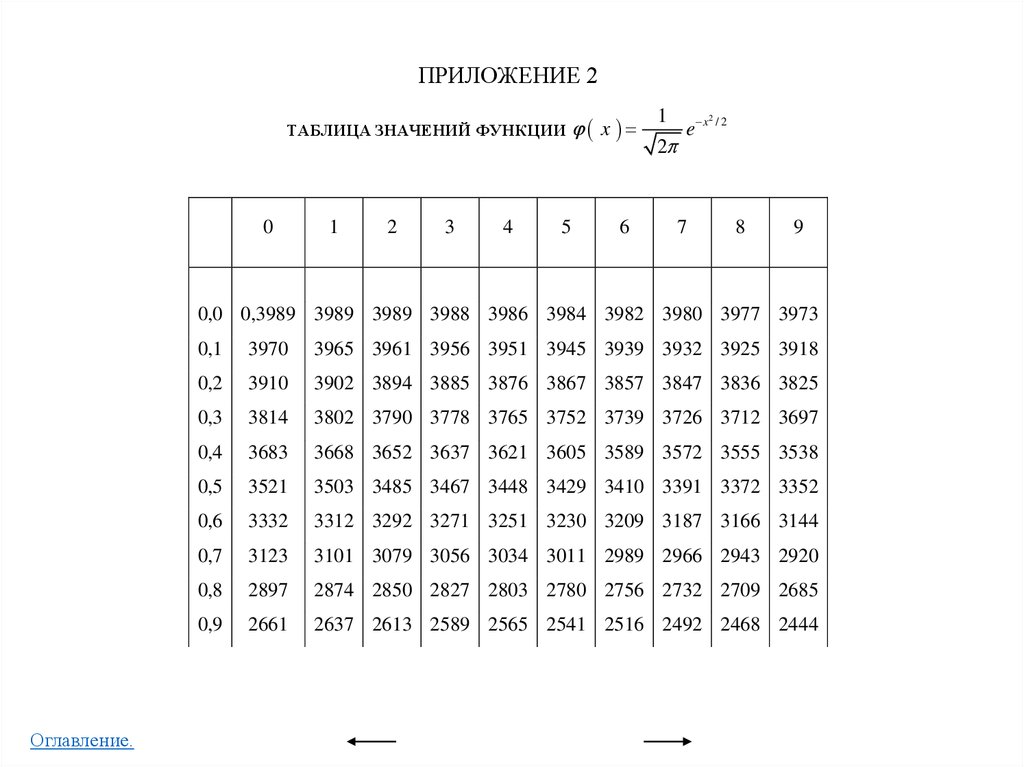
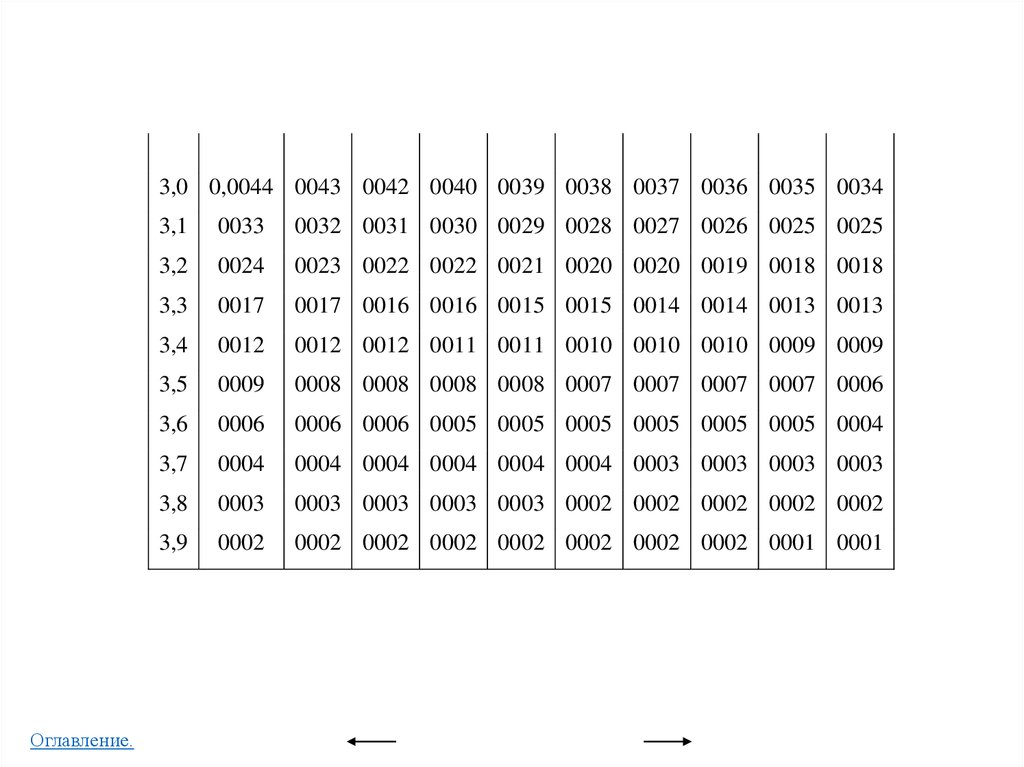
• Приложение 2
Таблица значений функции
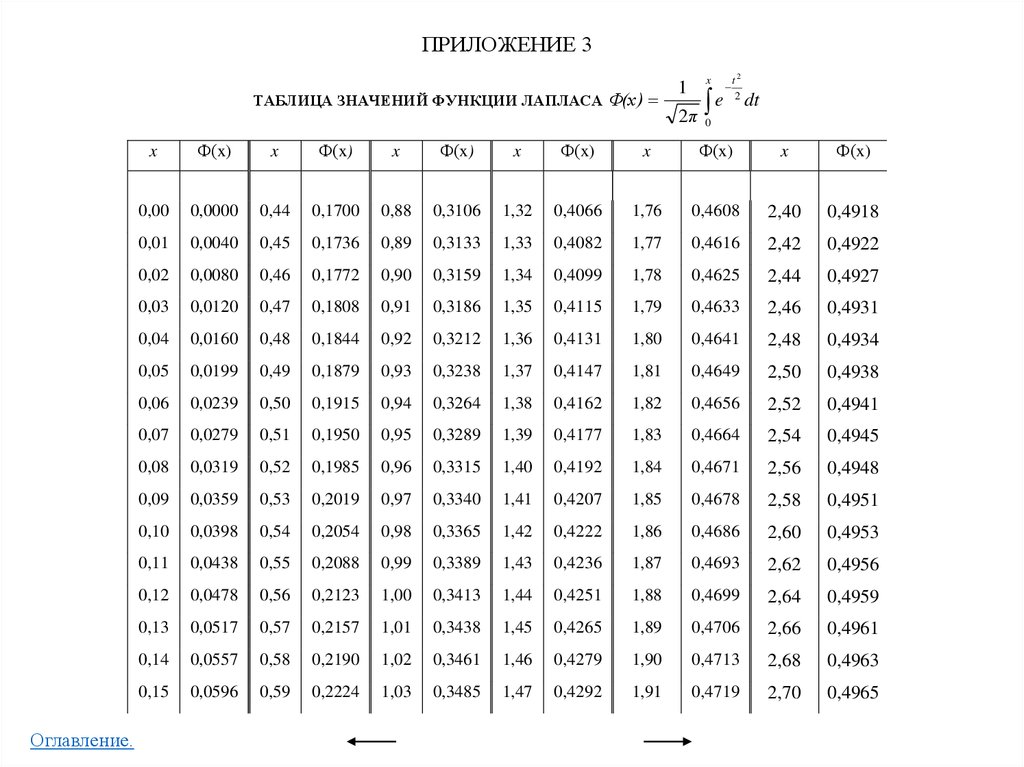
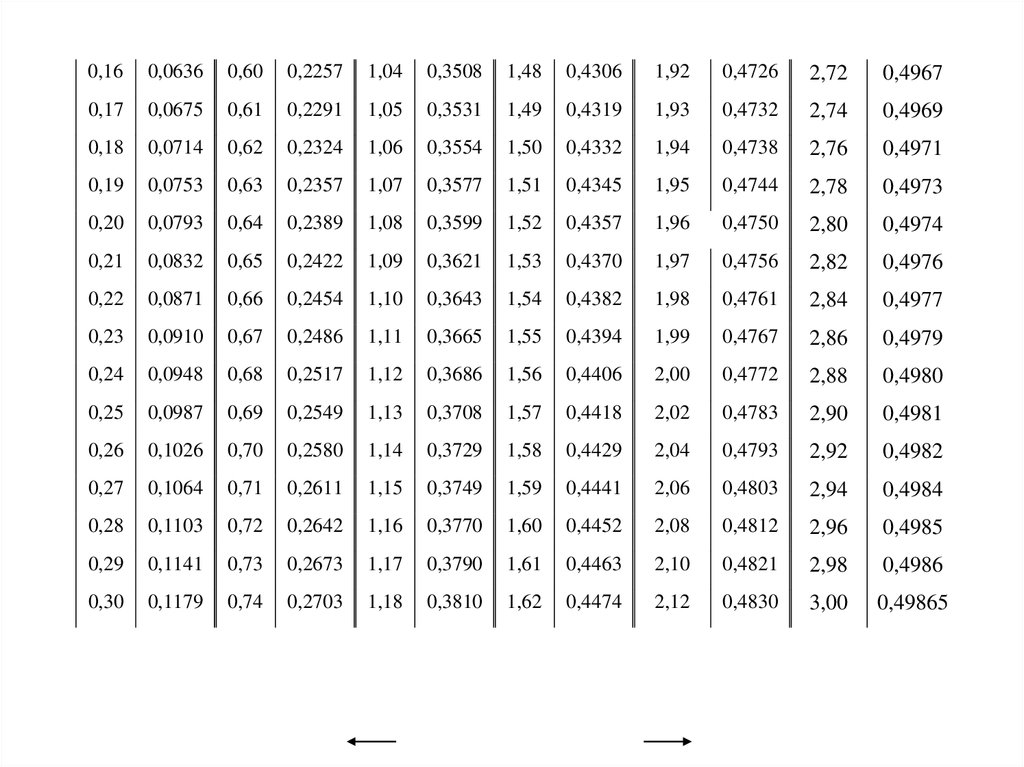
• Приложение 3
Таблица значений функции Лапласа
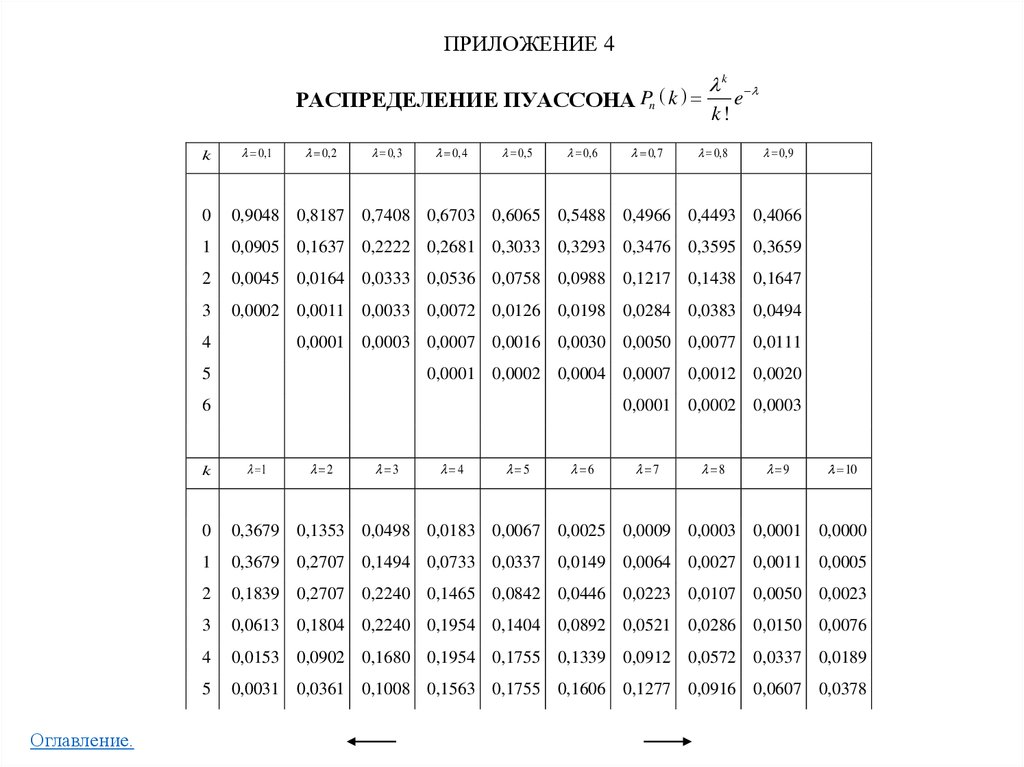
• Приложение 4
Распределение Пуассона
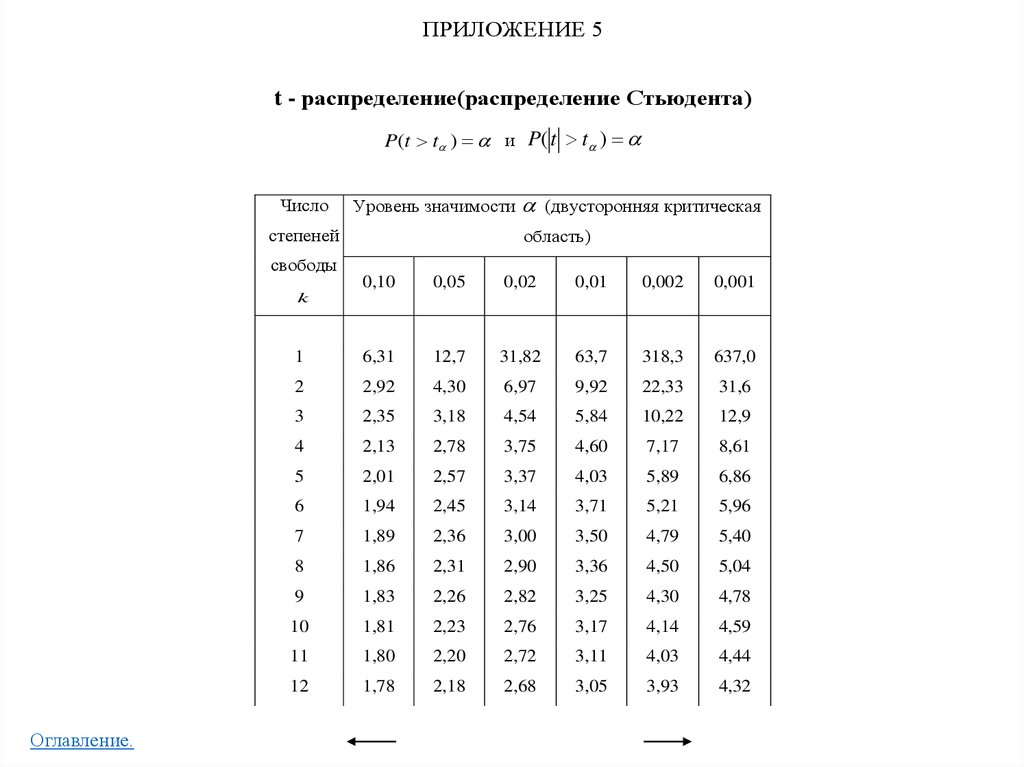
• Приложение 5
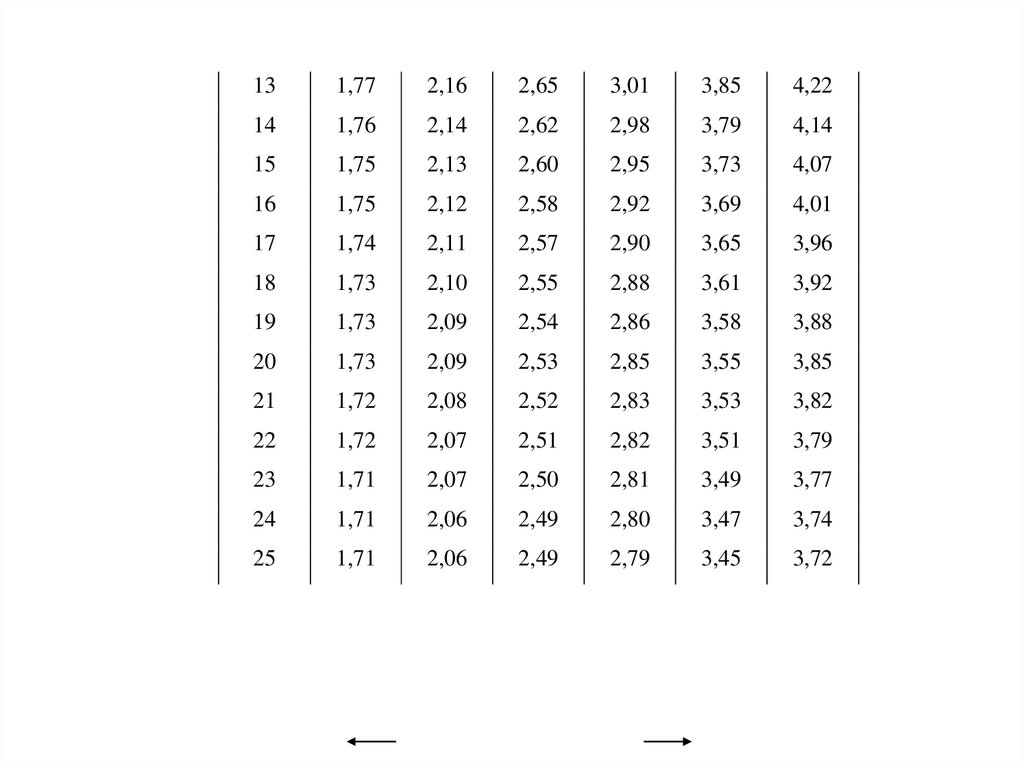
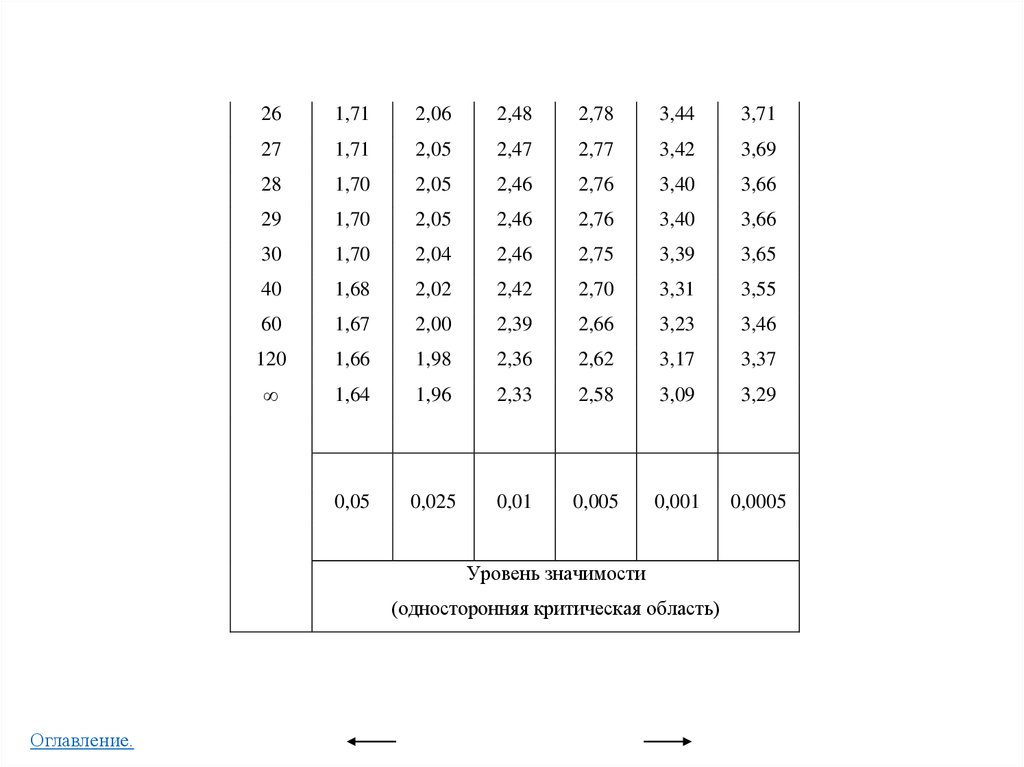
t - распределение (распределение Стьюдента)
• Приложение 6
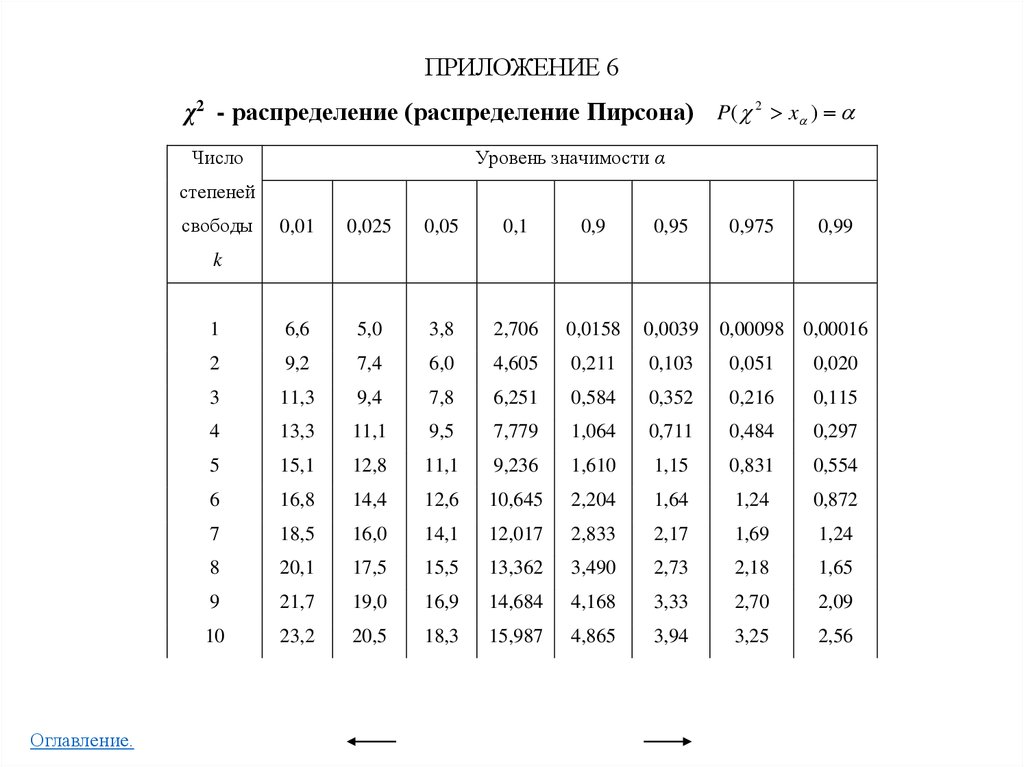
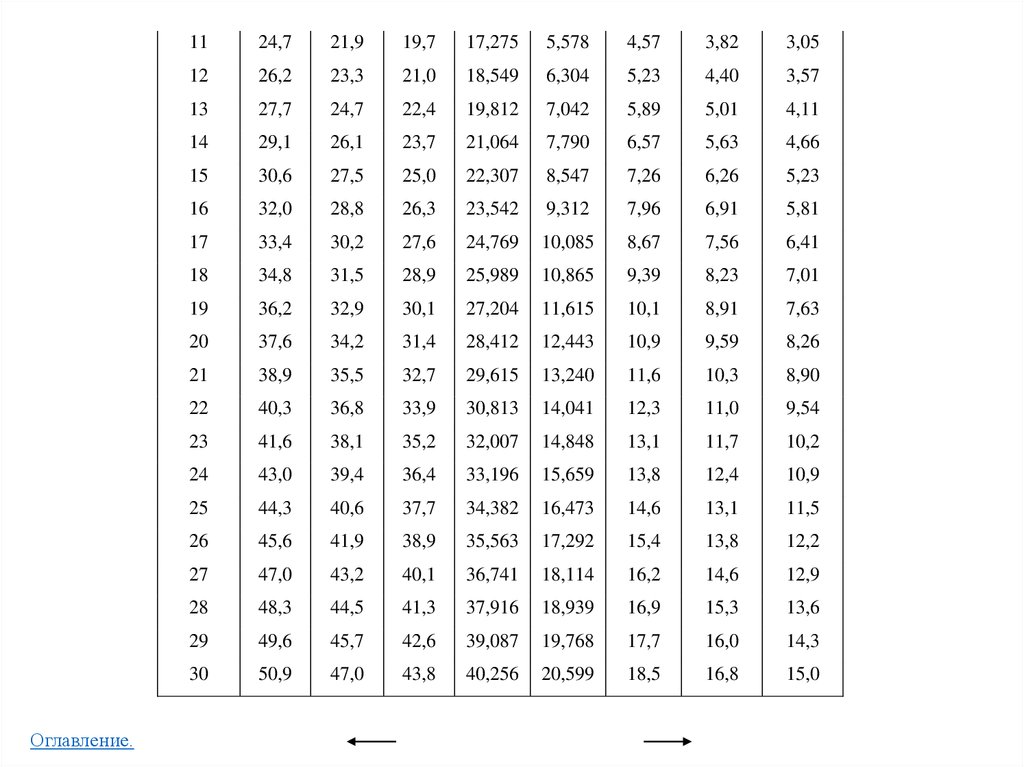
χ2 - распределение (распределение Пирсона)
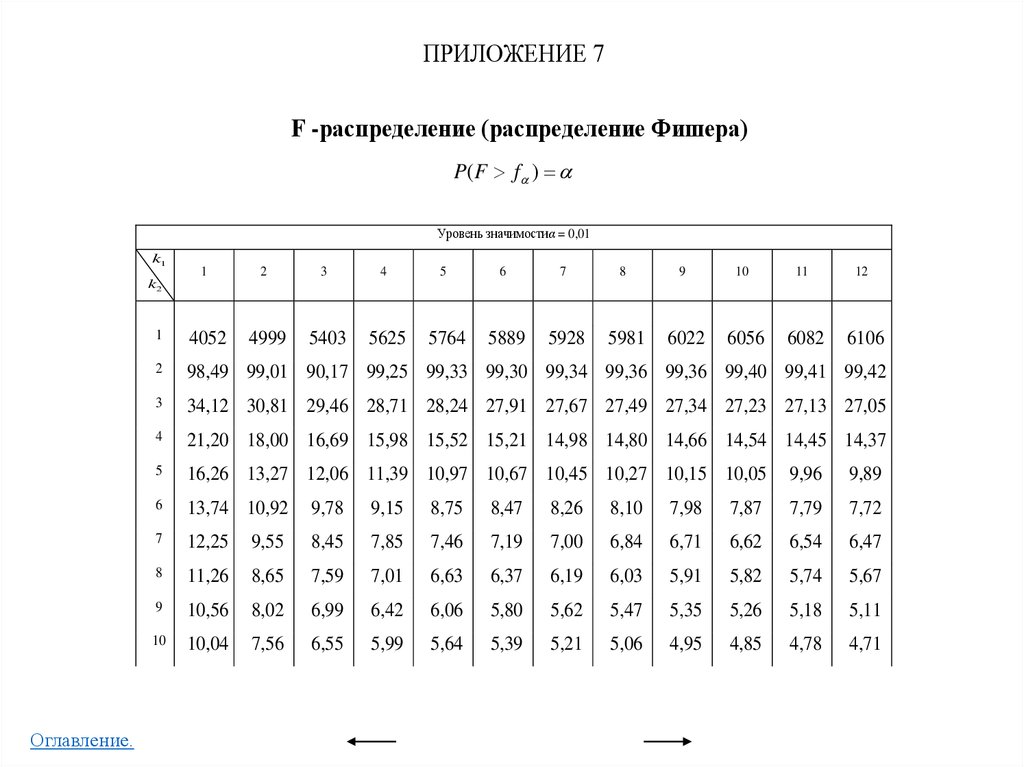
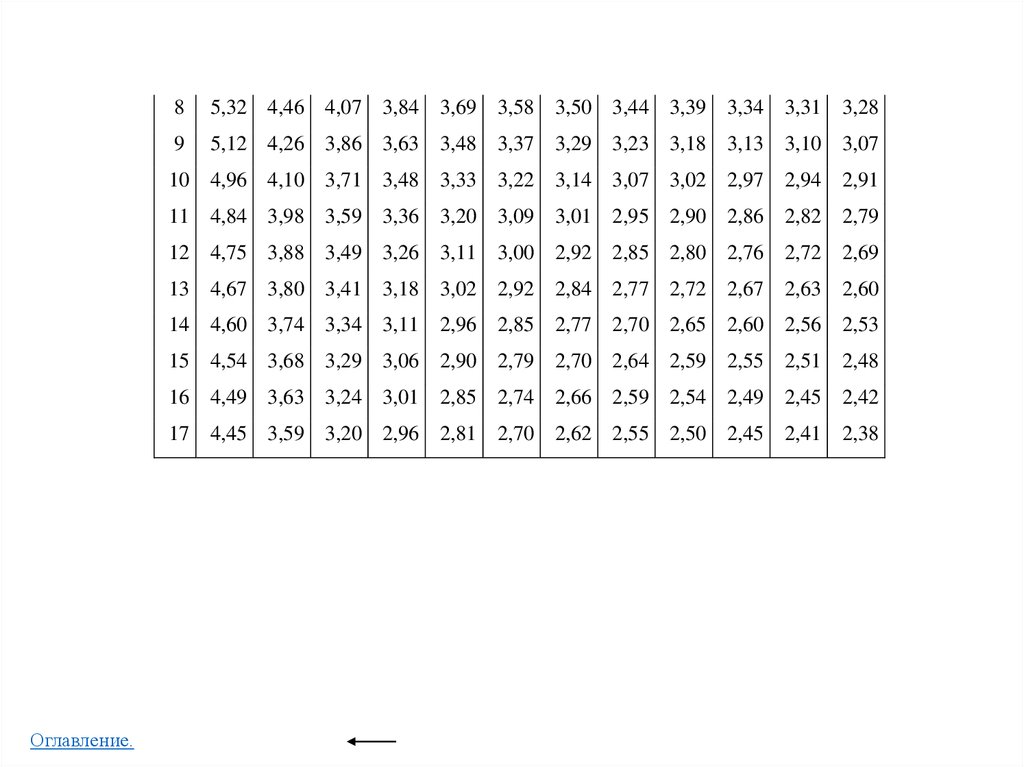
• Приложение 7
F -распределение (распределение Фишера)
5.
ПредисловиеПособие «Теория вероятностей и математическая статистика: практикум» предназначено
для обучения учащихся колледжей, получающих среднее специальное образование, и служит для
закрепления теоретического материала, формирования практических навыков решения задач по
теории вероятностей и освоения статистических методов обработки данных с использованием
современных
информационных
технологий.
Практикум
ориентирован
на
применение
математических методов в задачах прикладного характера и представляет собой руководство к
выполнению десяти лабораторно-практических работ по следующим разделам дисциплины:
– «Классическое, геометрическое и статистическое определения вероятностей событий»;
– «Теоремы сложения и умножения вероятностей независимых событий»;
– «Условная вероятность. Формула полной вероятности и формулы Байеса»;
– «Дискретные случайные величины. Биномиальный закон распределения»;
– «Повторение независимых испытаний»;
– «Непрерывные случайные величины»
– «Вариационные ряды, их графическое изображение»;
– «Точечные и интервальные оценки параметров распределения»;
– «Проверка параметрических гипотез»;
– «Проверка непараметрических гипотез».
Оглавление.
6.
Каждая лабораторно-практическая работа содержит краткиетеоретические сведения, образец решения и оформления типового
варианта задания, 30 вариантов практического задания одинаковой
степени сложности и контрольные вопросы. В разобранных задачах
приведены образцы решения типовых заданий как расчетными
методами, так и с использованием электронных таблиц Excel. В
пособии также содержатся все необходимые исходные данные,
рекомендуемая литература и справочные материалы (в виде
приложений).
Отметим, что лабораторно-практические работы 1-3 написаны И.Ю.
Мацкевич, работы 4-6 – Л.И. Тарусиной, а работы 7-10 – Н.П.
Петровой.
Авторский коллектив выражает благодарность Л.И. Майсене за
внимательное рецензирование данной работы и корректные замечания
7.
ЛАБОРАТОРНО-ПРАКТИЧЕСКАЯ РАБОТА 1КЛАССИЧЕСКОЕ, ГЕОМЕТРИЧЕСКОЕ И
СТАТИСТИЧЕСКОЕ
ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ СОБЫТИЙ
Цель работы:
-изучение основных понятий теории вероятностей;
-ознакомление с различными методами вычисления
вероятностей событий;
-практическое применение элементов комбинаторики
для вычисления вероятностей событий.
Оглавление.
8.
Краткие теоретические сведенияТеория вероятностей – это раздел математики, в котором изучаются
закономерности, присущие массовым случайным явлениям.
Комбинаторика – это раздел математики, в котором изучаются вопросы,
связанные с рассмотрением множеств и подсчётом числа различных комбинаций
из элементов этих множеств.
Пусть дано множество Е, содержащее n элементов. Число n называют
объемом множества Е.
Извлечение k (k ≤ n) элементов из множества Е называется выбором k
элементов, а сам извлеченный набор – выборкой объема k.
Правило произведения: если множество Е1 объёма n1, множество Е2 объёма
n2, …, множество Ек объёма nк, то число способов выбора по одному элементу из
каждого множества Е1, Е2, …, Ек равно n1 ⋅n2 ⋅...⋅nk.
Правило суммы: если множество Е1 объёма n1, множество Е2 объёма n2, …,
множество Ек объёма nк, то число способов выбора всех элементов из каждого
множества Е1, Е2, …, Ек равно n1 +n2 +...+nk.
9.
Следствие: если множества Е1, Е2, …, Ек содержат по n элементов каждое, точисло способов выбора по одному элементу из этих множеств равняется nk.
Перестановкой n элементов называется расположение этих элементов в
определенном порядке. Число перестановок из n элементов определяется
формулой
























































































































































































































































































 Математика
Математика








