Теория вероятностей и математическая статистика

1. Теория вероятностей и математическая статистика

2. Суть выборочного метода

Суть выборочного метода
заключается в том, что
по выборке делается вывод о
генеральной совокупности в
целом.

3. Выборочный метод является единственно возможным

1. Генеральная совокупность
бесконечна.
2. Объекты генеральной
совокупности уничтожаются
при измерении.
3. Измерения очень
дорогостоящи.

4. Ранжированный ряд

Ранжированным рядом
называется выборка,
упорядоченная по
возрастанию.

5. Обработка дискретной выборки

Если выборка сделана из
множества значений
дискретной случайной
величины, то она может
быть сгруппирована в
дискретный вариационный
ряд.

6. Варианты и частоты

Варианты хi - это
неповторяющиеся выборочные
значения.
Частота варианты n i - это
число, показывающее, сколько раз
варианта встречается в выборке.
Относительная частота
варианты
w i= n i / n.

7. Дискретный вариационный ряд

Дискретный вариационный ряд
или просто вариационный ряд –
это соответствие между
вариантами хi их частотами ni ;
или вариантами хi и их
относительными частотами wi

8. Дискретный вариационный ряд

xi
x1
x2
…
xk
ni
n1
n2
…
nk

9. Условие нормировки

k
n
n
i
i 1

10. Дискретный вариационный ряд

xi
x1
x2
…
xk
wi
w1
w2
…
wk

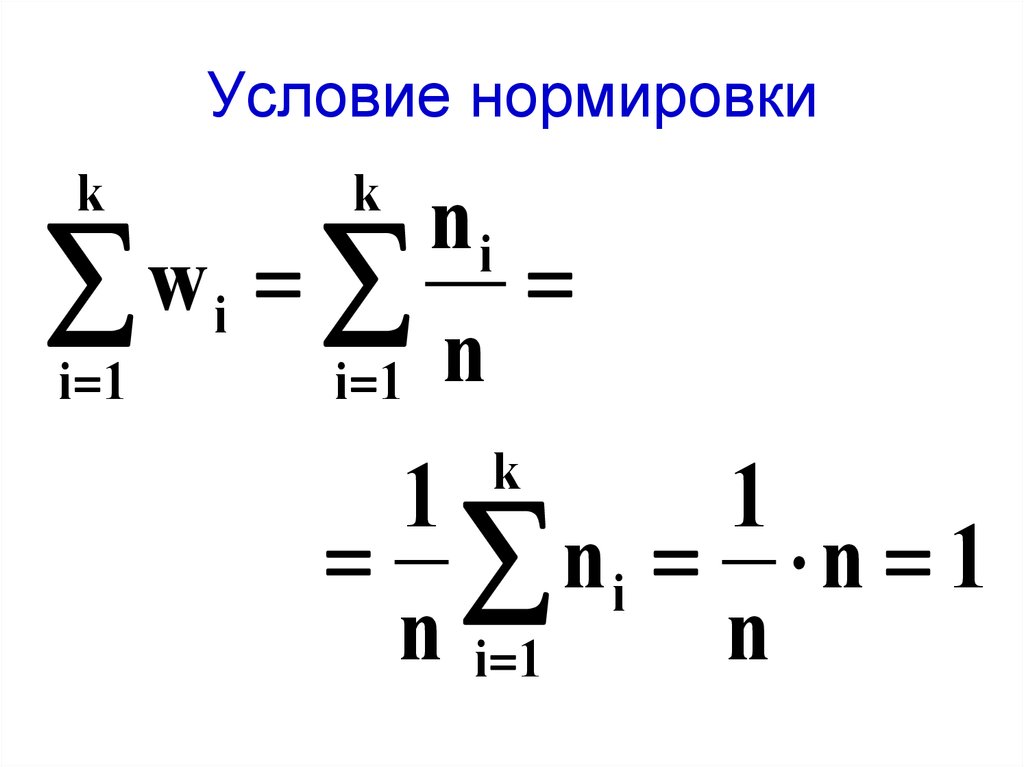
11. Условие нормировки

k
k
ni
w
i
i 1
i 1 n
k
1
1
ni n 1
n i 1
n

12. Интервальный ряд

Если выборка сделана из
множества значений
непрерывной случайной
величины, то она может быть
сгруппирована в
интервальный
вариационный ряд.

13. Интервальный ряд

Интервальный вариационный
ряд или просто интервальный
ряд – это соответствие между
частичными интервалами
(интервалами группировки) их
частотами (или
относительными частотами).

14. Интервальный ряд

аi – аi+1 а1 – а2 …
ni
n1
…
аk – аk+1
nk

15. Интервальный ряд

Частота интервала
аi – аi+1
- это число ni,
показывающее, сколько раз
варианта встречается внутри
данного интервала.

16. Накопленные частоты

Накопленной частотой
действительного числа х –
называется количество
выборочных данных,
лежащих левее х на
числовой оси.
Обозначается – n x

17. Накопленные частоты

Относительной накопленной
частотой действительного
числа х – называется число
nx
wx
n

18. Накопленные частоты

Накопленной частотой
интервала аi – аi+1
– называется количество
выборочных данных, лежащих от
начала выборки до конца данного
интервала. Обозначается:
ni
накопл

19. Графические представления выборки

Полигон частот – это
ломаная линия с узлами в
точках
.
или
(x i , ni )
(w i , ni )

20. Графические представления выборки

Гистограмма – это ступенчатая
фигура, состоящая из
прямоугольников,
основаниями которых
являются частичные
интервалы, а высоты
соответствуют частоте.

21. Графические представления выборки

Кумулята – это ломаная
линия, с узлами в точке
_______
( x i , n хi ) для дискретного
вариационного ряда и с
( a i , na i )
узлами в точках _______
для интервального ряда.

22. Эмпирическая функция распределения

Эмпирическая функция
распределения находится по
формуле:
n
Fn ( x )
x
n
Здесь n – это объем выборки; – это
накопленная частота числа х, т. е.
число выборочных данных, строго
меньших х.