Площа бічної та повної поверхонь конуса

1. Площа бічної та повної поверхонь конуса

2.

Конус
Назва цієї
фігури пішла від
грецького слова
«конос», так
греки називали
ялинкову
шишку.

3. Конус серед нас

4.

5. Конус – це тіло, отримане обертанням прямокутного трикутника навколо прямої, яка є нерухомим катетом.

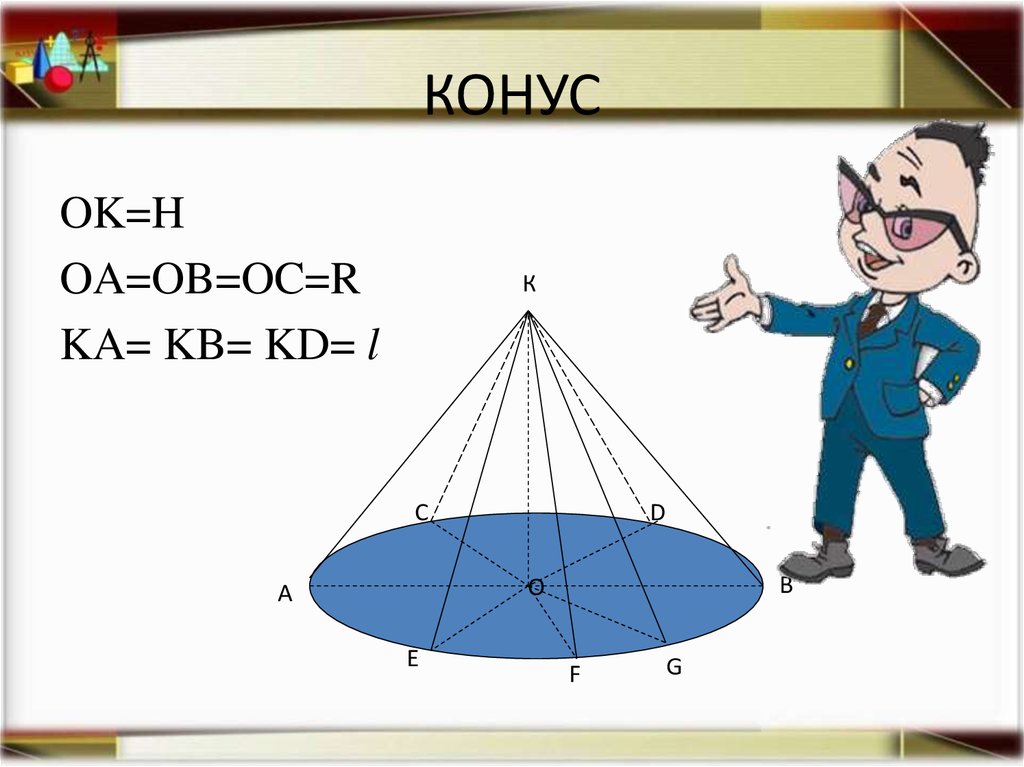
Це є одна з фігур обертання

6. КОНУС

OK=H
OA=OB=OC=R
KA= KB= KD= l
К
С
D
В
О
А
E
F
G

7.

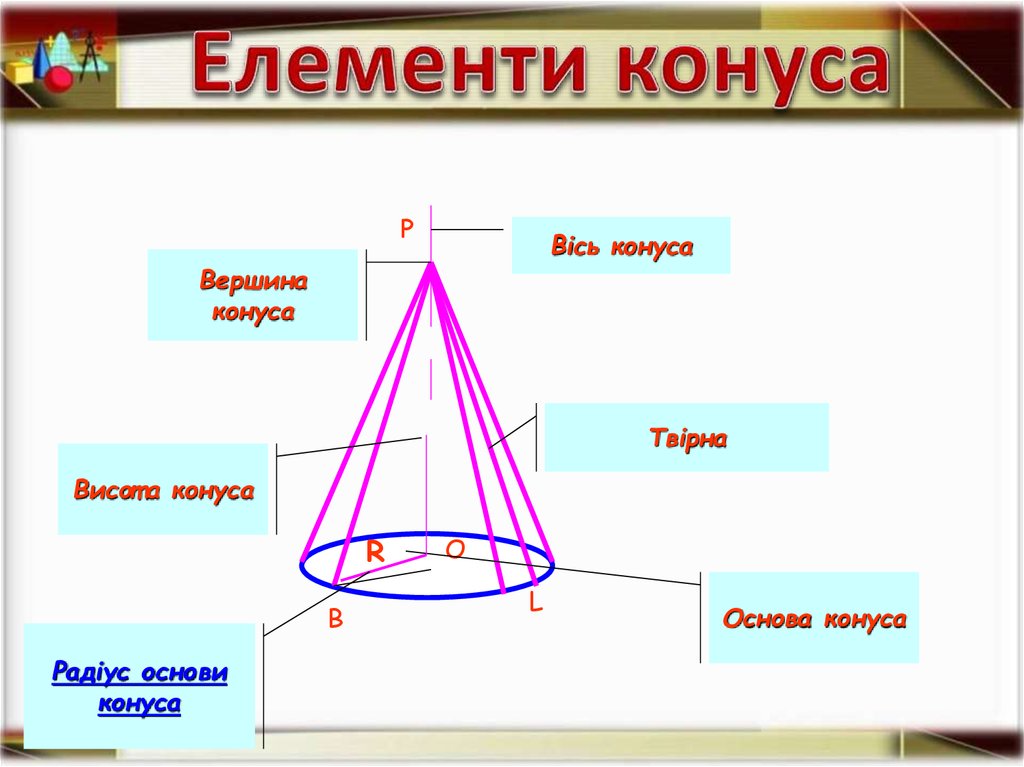
P
Вісь конуса
Вершина
конуса
Твірна
Висот а конуса
R
B
Радіус основи
конуса
O
L
Основа конуса

8. Розмітка БІЧНОЇ ПОВЕРХНІ КОНУСА –

AK = r
ПЛОЩА КРУГА:
S = πr2

9. ФОРМУЛА ПЛОЩІ БІЧНОЇ ПОВЕРХНІ КОНУСА:

Sб. = π R l
R – радіус основи,
l –твірна конуса.

10. ФОРМУЛА ПЛОЩІ ПОВНОЙ ПОВЕРХНІ КОНУСА

К
Sп = Sб + Sосн
2
Sп = πRl + π R
Sп = π R(R+l)
О
А
В

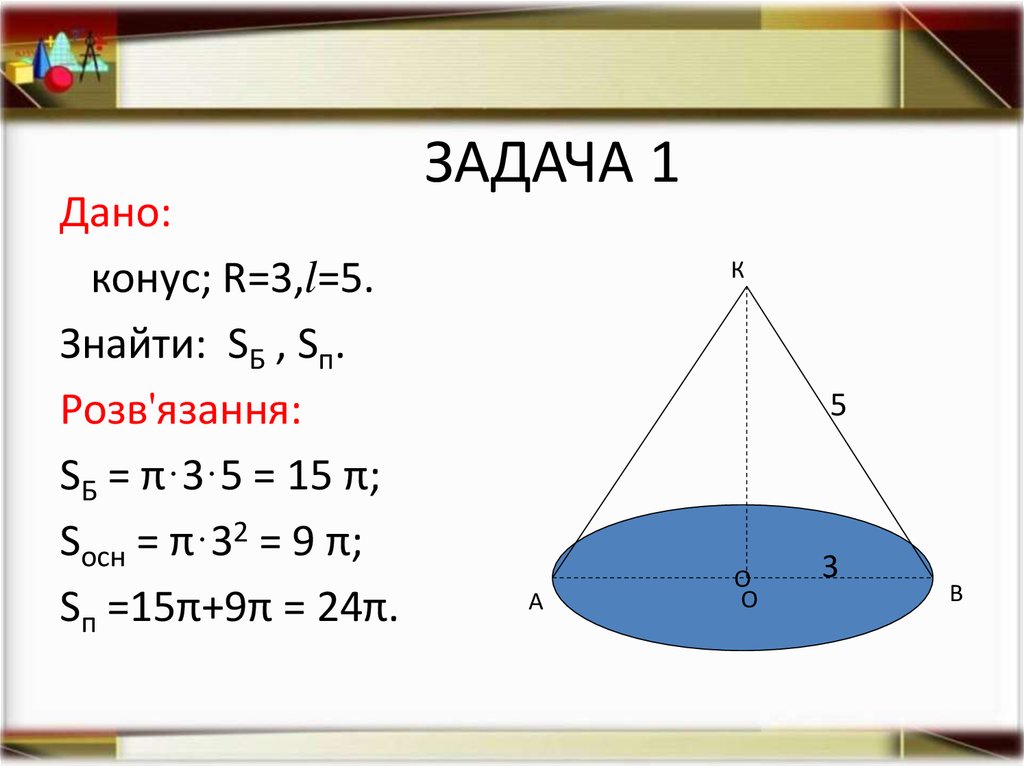
11. ЗАДАЧА 1

Дано:
конус; R=3,l=5.
Знайти: SБ , Sп.
Розв'язання:
SБ = π·3·5 = 15 π;
Sосн = π·32 = 9 π;
Sп =15π+9π = 24π.
ЗАДАЧА 1
К
5
А
О
О
3
В

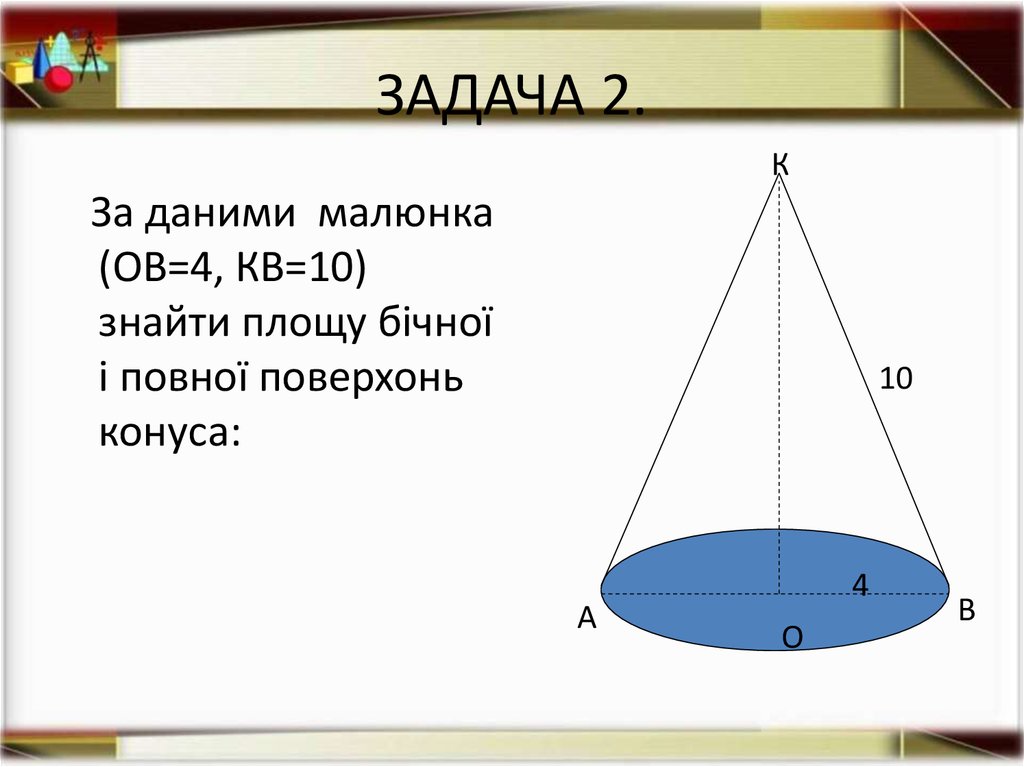
12. ЗАДАЧА 2.

К
За даними малюнка
(ОВ=4, КВ=10)
знайти площу бічної
і повної поверхонь
конуса:
10
А
4
О
В

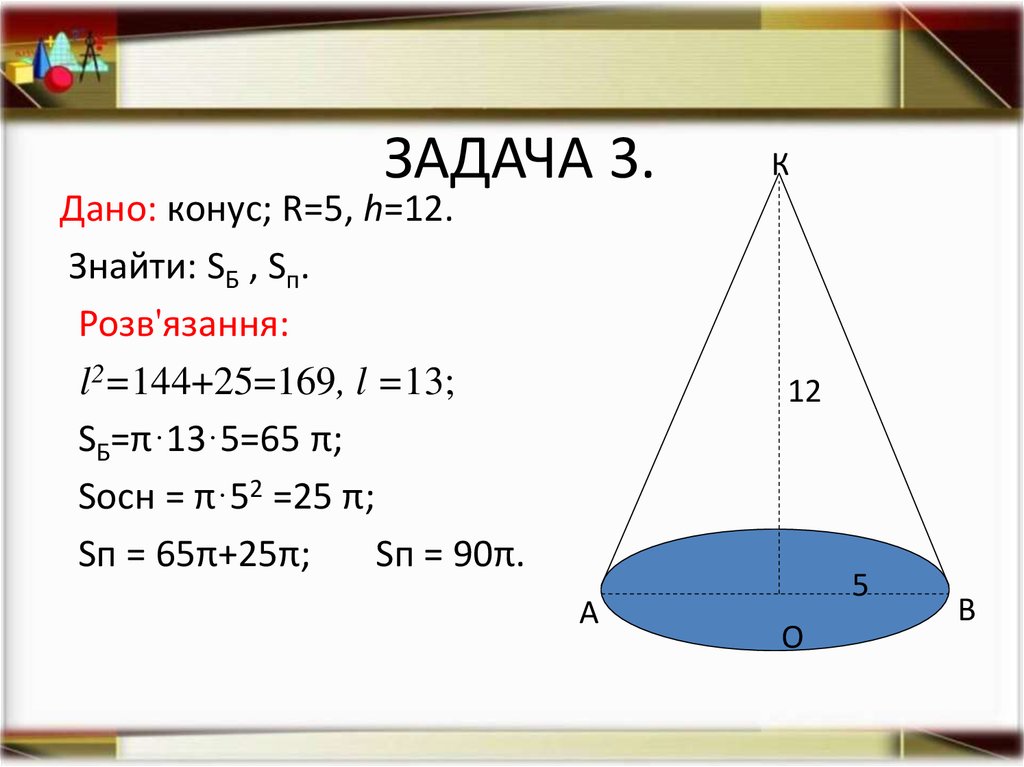
13. ЗАДАЧА 3.

Дано: конус; R=5, h=12.
Знайти: SБ , Sп.
Розв'язання:
l2=144+25=169, l =13;
SБ=π·13·5=65 π;
Sосн = π·52 =25 π;
Sп = 65π+25π;
Sп = 90π.
К
12
А
5
О
В

14. ЗАДАЧА 4.

За даними малюнка
(ОВ=6, ∟АКО=30о)
знайдіть площу
бічної і повної
поверхонь конуса:
К
о
30
А
6
О
В

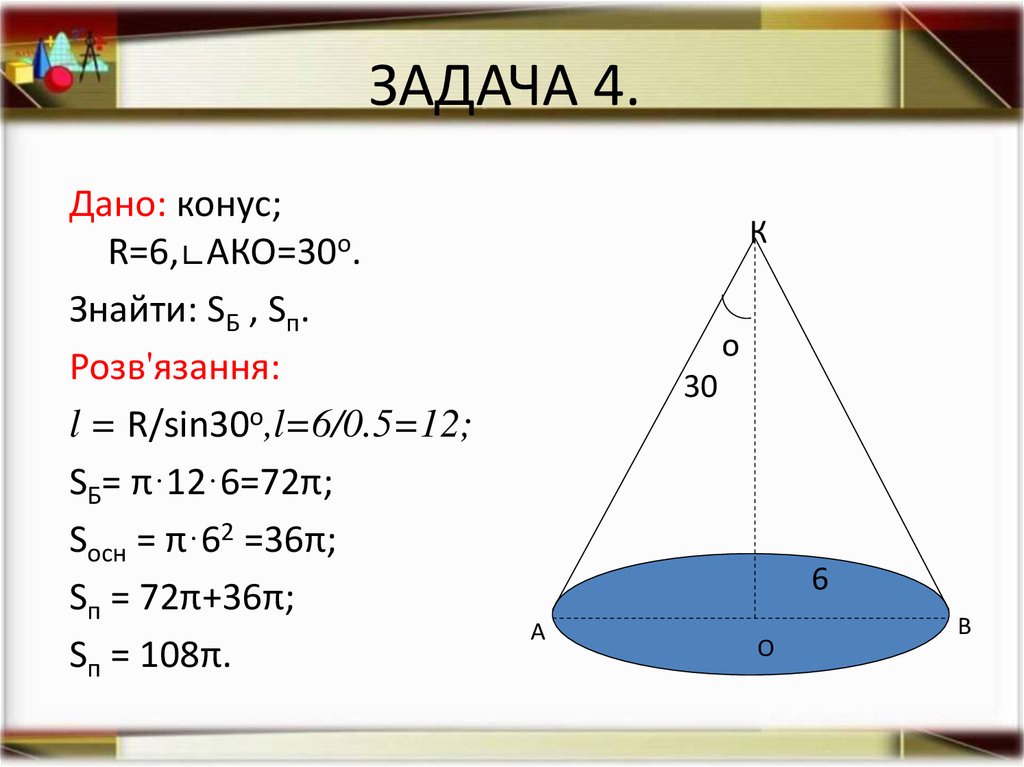
15. ЗАДАЧА 4.

Дано: конус;
R=6,∟АКО=30о.
Знайти: SБ , Sп.
Розв'язання:
l = R/sin30о,l=6/0.5=12;
SБ= π·12·6=72π;
Sосн = π·62 =36π;
Sп = 72π+36π;
Sп = 108π.
К
о
30
6
А
О
В

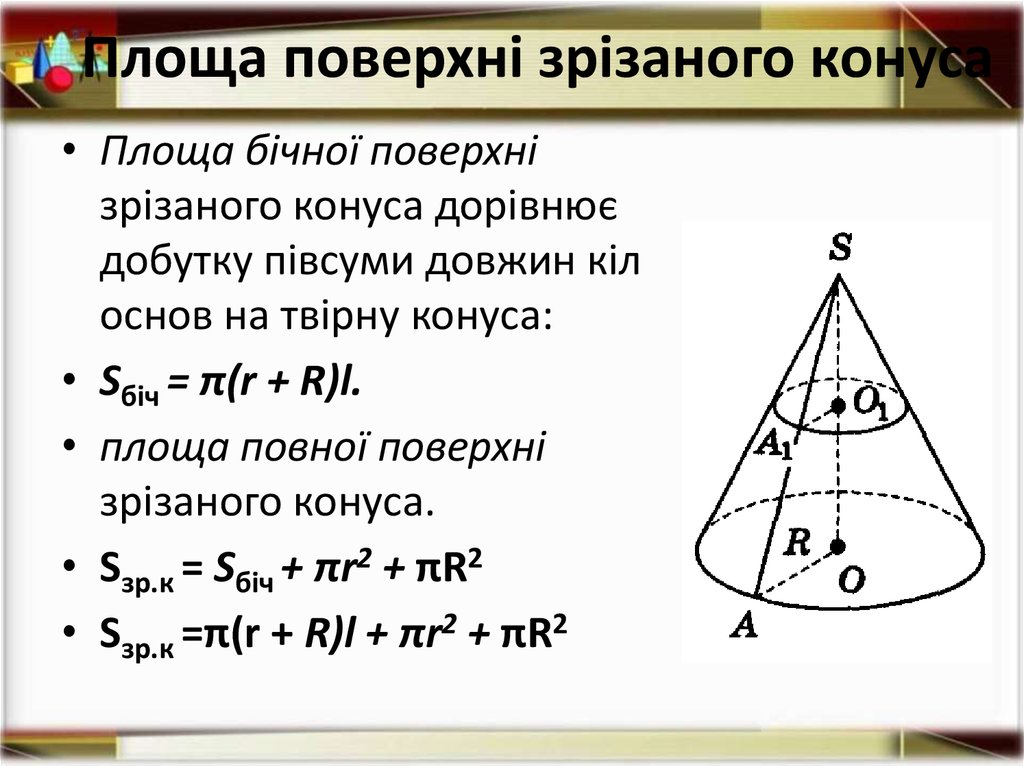
16. Площа поверхні зрізаного конуса

• Площа бічної поверхні
зрізаного конуса дорівнює
добутку півсуми довжин кіл
основ на твірну конуса:
• Sбіч = π(r + R)l.
• площа повної поверхні
зрізаного конуса.
• Sзр.к = Sбіч + πr2 + πR2
• Sзр.к =π(r + R)l + πr2 + πR2

17. Домашнє завдання:

• Зробити конспект лекції.
• Проаналізувати розв'язки задач і заповнити
пропуски у їх розв'язанні.
• Виконати індивідуальні завдання (10
варіантів)

18.

• Задача № 1. Конусоподібну палатку
висотою 3,5 м і діаметром основи 4 м
покрито тканиною. Скільки квадратних
метрів тканини пішло на палатку?
• Задача № 2. Дах силосної башти має форму
конуса. Висота доху 2 м, а діаметр башти 6
м. Знайти поверхню даху.

19. Розв'язання задачі № 1

Нехай h = 3,5 м і D = ... м,
тоді S = πrl, де r — радіус основи конуса;
r=………. =2 (м);
l — твірна конуса;
l=…………………………………………………(м).
• S = π ·2 · ... 25,3 (м2).
• Відповідь. 25,3 м2.

20. Розв'язання задачі № 2

Нехай h = ... і D = 6 м,
тоді S = πrl, де r — радіус основи конуса;
r = …………………… (м);
l — твірна конуса;
l = ……………………………………………………………(м).
S = 3,14 · 3 · 3,6 = ... (м2).
Відповідь. 33,98 м2.