Теплопередача при стационарном режиме

1. Лекция №8. Теплопередача при стационарном режиме

Теплопередачей называется теплообмен между двумя средами через разделяющую их
перегородку. Теплопередача является сложным видом теплообмена, в котором участвуют
две среды и тело. Кроме того, в нём действуют одновременно и совместно все
элементарные
явления
переноса
теплоты
(теплопроводность,
конвекция,
лучеиспускание).
Количество переданной теплоты теплопередачей при стационарном режиме
определяется по основному уравнению теплопередачи:
Q = K F t, Вт,
где Q – количество переданной теплоты, Вт.
t – tг – tх, оС.
tг – температура горячего теплоносителя, оС;
tх – температура холодного теплоносителя, оС;
F – теплообменная поверхность, м2;
K – коэффициент теплопередачи, размерность которого получается из
основного уравнения:
[K] = [Q/F t] = [Вт/м2 град]
Коэффициент теплопередачи представляет собой количество теплоты, переданной через
единицу поверхности в единицу времени от одного теплоносителя к другому при
разности температур между ними в один градус. Коэффициент теплопередачи связывает
между собой коэффициент теплопроводности и теплоотдачи.

2. Теплопередача через плоскую стенку

Рассмотрим случай, когда две среды разной температуры разделены однородной
плоской стенкой. Коэффициент теплопроводности стенки - и толщина её - .
Температура - tC1 и tC2, причём tC1 > tC2. Температура поверхностей стенки
неизвестны, обозначим их как tn1 и tn2. Суммарный коэффициент теплоотдачи со
стороны горячего теплоносителя равен 1, а со стороны холодного - 2.
По условию задачи температурное
поле
одномерно,
режим
стационарный. В этом случае вся
теплота, переданная от горячего
теплоносителя к поверхности
стенки, проходит сквозь стенку и
отдаётся
холодному
теплоносителю, т.е. указанные
количества теплоты равны между
собой.
Следовательно, для теплового потока q, где q = Q/F , можно написать систему
из трёх уравнений:

3. Теплопередача через плоскую стенку

(1)
Из уравнений (1) находятся частные температурные напоры:
(2)
После сложения левых и правых частей уравнений (2) получается выражение
для полного температурного напора
tC1 - tC2 = q(1/ 1 + / + 1/ 2),
(3)
откуда определяется значение удельного теплового потока:
(4)

4. Теплопередача через плоскую стенку

Согласно формуле (4), тепловой поток прямо пропорционален разности
температур между двумя теплоносителями и обратно пропорционален сумме
термических сопротивлений.
Вводя обозначение: К = 1/(1/ 1 + / + 1/ 2) в выражение (4), получим:
q = K(tC1 - tC2)
Величина К называется коэффициентом теплопередачи. Он устанавливает связь
между элементарными видами теплообмена через коэффициенты теплоотдачи и
коэффициенты теплопроводности.
Величина, обратная коэффициенту теплопередачи, называется полным
термическим сопротивлением теплопередачи:
1/K = 1/ 1 + / + 1/ 2 , [м2 град/Вт]
где / - термическое сопротивление стенки
1/ 1 и 1/ 2 - являются термическими сопротивлениями теплоотдачи от
горячего теплоносителя к холодному.

5. Теплоотдача через цилиндрическую стенку

Цилиндрическая стенка разделяет горячую и холодную жидкости (с tC1 - tC2).
Температуры поверхностей стенки неизвестны, обозначим их через tn1 и tn2.
Коэффициент теплоотдачи от горячей жидкости, протекающей внутри трубы,
равен 1, а к холодной - 2.
В условиях стационарного режима количество теплоты, отданное горячей и
воспринятое холодной жидкостями, одно и то же, следовательно, можно
написать:
(1)
Решив эти уравнения относительно разности температур, получим:
(2)

6. Теплоотдача через цилиндрическую стенку

Складывая уравнения (2), получим полный температурный напор:
(3)
Откуда значение теплового потока
(4)
Введём следующее обозначение
(5)
После подстановки этого равенства в (4) окончательно получим:
ql = Кl (tC1 - tC2),
здесь Кl – коэффициент теплоотдачи, отнесённый к единице длины трубы.

7. Средний температурный напор

Процессы теплопередачи при постоянных температурах распространены
относительно мало. Такие процессы протекают, например, в том случае, если с
одной стороны стенки конденсируется пар, а с другой – кипит жидкость.
Наиболее часто теплопередача в промышленной аппаратуре протекает при
переменных температурах теплоносителей.
Температуры теплоносителей обычно изменяются вдоль поверхности,
разделяющей их стенки.
Теплопередача при переменных температурах зависит от взаимного
направления движения теплоносителей. В непрерывных процессах теплообмена
возможны следующие варианты направления движения жидкостей друг
относительно друга вдоль разделяющей их стенки:
1) параллельный ток, или прямоток, при котором теплоносители движутся в
одном и том же направлении;
2) противоток, при котором теплоносители движутся в противоположных
направлениях;
3) перекрёстный ток, при котором теплоносители движутся взаимно
перпендикулярно друг другу;
4) смешанный ток, при котором один из теплоносителей движется в одном
направлении, а другой – как прямотоком, так и противотоком к первому.

8. Средний температурный напор

Движущая сила процессов теплопередачи при переменных температурах
изменяется в зависимости от вида взаимного направления движения
теплоносителей. Поэтому в уравнение теплопередачи следует подставлять
среднее значение температурного напора
Q = K F tm
(1)
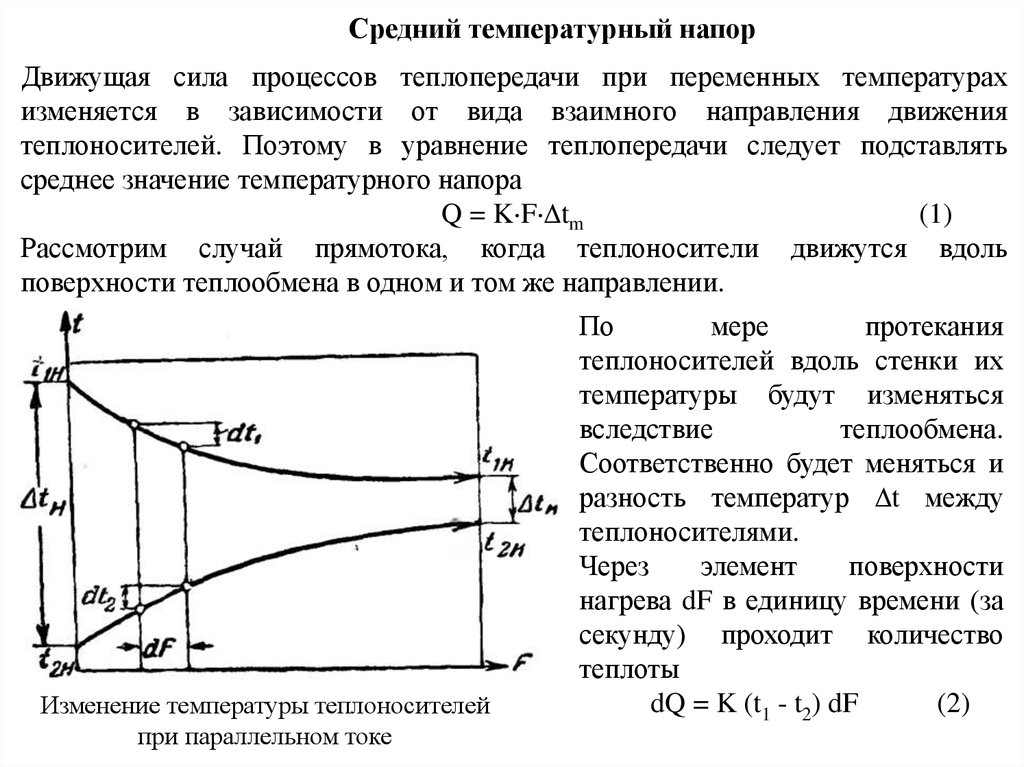
Рассмотрим случай прямотока, когда теплоносители движутся вдоль
поверхности теплообмена в одном и том же направлении.
Изменение температуры теплоносителей
при параллельном токе
По
мере
протекания
теплоносителей вдоль стенки их
температуры будут изменяться
вследствие
теплообмена.
Соответственно будет меняться и
разность температур t между
теплоносителями.
Через
элемент
поверхности
нагрева dF в единицу времени (за
секунду) проходит количество
теплоты
dQ = K (t1 - t2) dF
(2)

9. Средний температурный напор

При этом температура более нагретой жидкости понизится на
dt1 = - dQ/G1C1
(3)
менее нагретой повысится на dt2 = - dQ/G2C2, где
G1 – количество протекающей в единицу времени горячей жидкости
C1 – её теплоёмкость
G2 – количество протекающей в единицу времени холодной жидкости
C2 – её теплоёмкость
Знак “минус” указывает на охлаждение более нагретого теплоносителя в
процессе теплообмена.
Произведение G C назовём водяным эквивалентом и обозначим G1 C1 = W1;
G2 C2 = W2
и
1/W1 + 1/W2 = m
(4)

10. Средний температурный напор

Изменение температурного напора получим, вычитая величину изменения
температуры менее нагретой жидкости из величины изменения температуры
более нагретой жидкости
откуда dQ = - d(t1 - t2)/m
(5)
Подставив найденное значение (5) в уравнение (2) получим
d(t1 - t2)/m = - K (t1 - t2) dF
(6)
Заменим t1 – t2 на t и разделим переменные на t
d t/ t = - K m dF
(7)

11. Средний температурный напор

Уравнение (7) можно проинтегрировать в пределах от tнач до tконеч и от 0 до F
(8)
ln tкон / tнач = - mRT
где tнач – (t1нач – t2нач) начальная разность температур,
tкон – (t1кон – t2кон) конечная разность температур.
Уравнение теплового баланса для элемента поверхности df имеет вид
Q = G1 C1 (t1нач – t1кон) = G2 C2 (t2кон - t2нач)
а так как
G1 C1 = W1, G2 C2 = W2, из уравнения (10) находим
Q/W1 = t1нач – t1кон и W2 = t2кон - t2нач
Складывая эти выражения и учитывая уравнение (4) получим
(9),
(10),
(11)
Q(1/W1 + 1/W2) = (t1нач – t1кон) + (t2кон - t2нач),
откуда
m = tнач - tконеч/Q
(12)

12. Средний температурный напор

Подставляя значение m в уравнение (9) получим
(13)
откуда
(14)
Сравнивая (14) с основным уравнением теплоотдачи (1), получим
(15)
(16)
Уравнение (16) остаётся верным и для определения среднелогарифмического
температурного напора при движении жидкости противотоком.

13. Средний температурный напор

Если температура рабочих жидкостей вдоль
незначительно, т.е. удовлетворяется условие
поверхности
изменяется
tнач / tкон < 2, то средний температурный напор можно вычислять как среднее
арифметическое из крайних напоров
tср = ( tнач - tкон)/2
Для смешанного тока и перекрёстного тока
tm = t tпр, где t – поправочный коэффициент к средней разности
температур tпр, вычисленный для противотока.

14. Определение средних температур теплоносителей

В технических расчётах температуру каждого теплоносителя усредняют по
длине трубы. Например, обозначим через T – температуру горячего
теплоносителя и через t – холодного теплоносителя. Если
t = tк – tн < T = Tн – Tк, то
tср = 0,5(tн – tк)
Tср = tср + tm
Если t > T, то Tср = 0,5(Tк + Tк)
tср = Tср - tm
Если задана температура поверхности стенки, соприкасающейся с жидкостью,
то
tср.ж = tст tm, где tm – средняя разность температур между стенкой и
жидкостью.

15. Тепловая изоляция

Для
снижения
теплопередачи
необходимо
увеличить
термическое
сопротивление. Это достигается путём нанесения на стенку слоя тепловой
изоляции.
Тепловой изоляцией называется всякое вспомогательное покрытие, которое
способствует снижению потери теплоты в окружающую среду. Выбор и расчёт
изоляции производится с учётом соображений экономического характера и
требований технологии и санитарии.
Толщина изоляции для плоских стенок определяется из формулы:
Для трубопроводов из формулы:
где d2 – диаметр изолированного трубопровода.

16. Тепловая изоляция

Для трубопроводов определение толщины изоляции усложняется тем, что d2 в
расчётное уравнение входит не только в форме ln d2/d1, но и в виде члена 1/ 2d2.
Тепловые
потери
изолированных
трубопроводов
уменьшаются
не
пропорционально увеличению толщины изоляции. Это обстоятельство
объясняется тем, что при увеличении толщины термическое сопротивление слоя
изоляции увеличивается
а термическое сопротивление теплоотдачи в окружающую среду уменьшается:
Во избежание большой толщины при изоляции трубопроводов применяют
материалы с малым коэффициентом теплопроводности. Максимальные
тепловые потери наблюдаются при некотором значении диаметра, который
называется критическим диаметром изоляции.
d2кр = 2 / 2 , где - теплопроводность изоляции
2 – коэффициент теплоотдачи от поверхности в
окружающую среду.