Позициялық және метрикалық есептер

1. Позициялық және метрикалық есептер

2.

• Сызба геометрия пәні негізгі екі есептерді шешумен
айланысады. Бұл есептерді позициялық
(тұрғылықты) және метрикалық (өлшем) есептер
деп атайды.
• Позициялық есептер дегеніміз - геометриялық
фигуралардың сызбалары арқылы олардың
кеңістіктегі өзара орналасуын анықтайтын есептер.
Позициялық есептер түрлеріне нүкте мен түзудің,
түзу мен түзудің, нүкте мен жазықтықтың, түзу мен
жазықтықтың, жазықтық пен жазықтықтың, жазықтық
пен дене бетінің, екі дене бетінің өзара орналасу
есептері жатады.
• Ал метрикалық есептер дегеніміз - геометриялық
фигуралардың сызбалары арқылы олардың
кеңістіктегі өзара қашықтықтарын, олардың
арасындағы бұрышы мен олардың ауданын, нақты
шамасын т.с.с жағдайын анықтайтын есептер.

3. Позициялық есептер

• Егер позициялық есептер күрделі емес оңай
есеп болса, онда есептің шешуін жалпы
әдістердің көмегімен шығарады. Бұл
параграфта кеңістіктегі нүкте мен түзу
сызықтың өзара орналасуы, кеңістіктегі түзу
сызықтардың өзара орналасуы, кеңістіктегі екі
жазықтықтың өзара орналасуы және
кеңістіктегі түзу мен жазықтықтың өзара
орналасулары сияқты позициялық есептерді
қарастырамыз.

4. Нүкте мен түзу сызықтың өзара орналасулары

5. Түзу сызықтардың өзара орналасулары

6.

7. Екі жазықтықтың өзара орналасуы

П2
П2
П2
Q2
P2
Q2
N2
Q2
D2
А2
F2
12
N2
E2
N1
М2
Qх
Pх
С2
P1
F1
D1
М1
П1
4 2 62
72
52
G2
Pх
P1
Q1
22 В
2
32
P2
P2
Qх
К2
П1
31
A1
П1
71
21
C1
N1
E1
B1
K1
11
Q1
41
G1
51 61

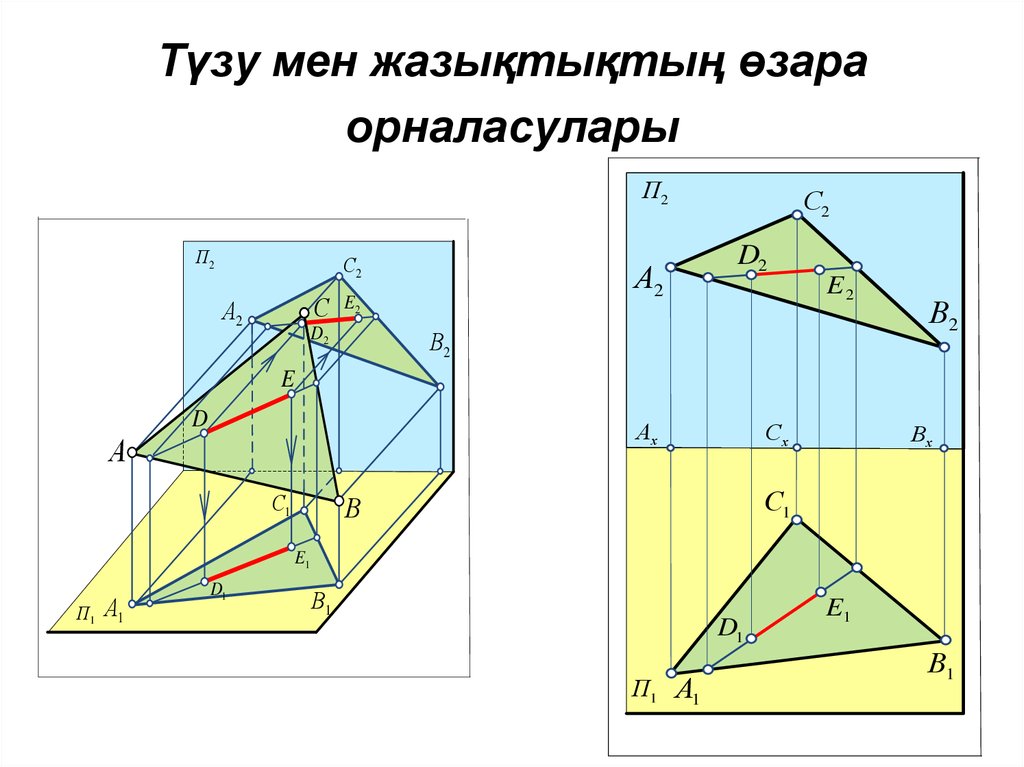
8. Түзу мен жазықтықтың өзара орналасулары

П2
П2
С2
С
А2
А2
E2
D2
С2
D2
E2
В2
В2
E
D
Ах
А
С1
Сх
Вх
С1
В
E1
П1
А1
D1
В1
D1
П1 А1
В1
E1
В1

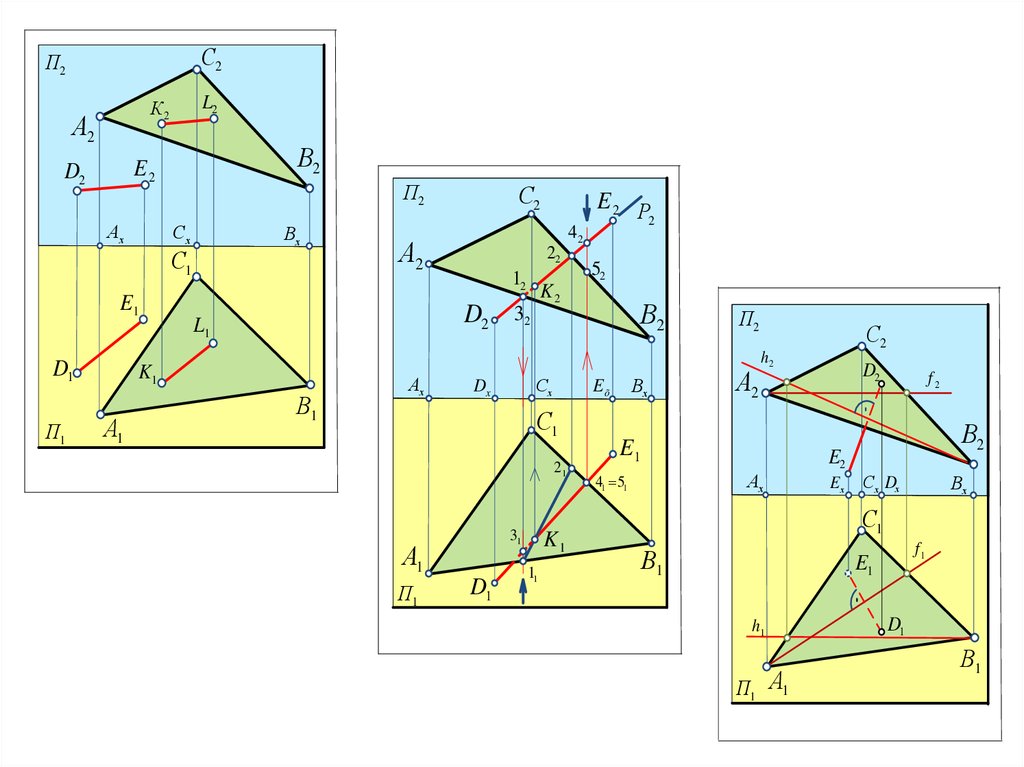
9.

С2
П2
L2
К2
А2
В2
E2
D2
Ах
П2
Сх
Вх
С1
E1
D1
П1
K1
А1
В1
С2
42
А2
22
12
D2
L1
В1
Ах
K2
Сх
21
В1
П1
В2
31
K1
11
Вх
Eõ
С1
D1
52
32
Dx
А1
E2 Р
2
П2
А2
С2
h2
E1
Ах
41 51
D2
f2
В2
E2
Eх
Вх
Сх Dх
С1
В1
f1
E1
h1
П1 А1
В1
D1
В1

10. Метрикалық есептер

• Егер шығаратын метрикалық есептер оңай
есеп болса, онда есепті шешуін жалпы
әдістердің көмегімен шығарады. Осыған
байланысты бұл параграфта кеңістіктегі
орналасқан түзу сызықтың нақты шамасы мен
түзудің проекция жазықтықтарына жасайтын
бұрыштарын, нүкте мен жазықтықтың ара
қашықтығы сияқты метрикалық есептерге
мысалдар қарастырамыз.

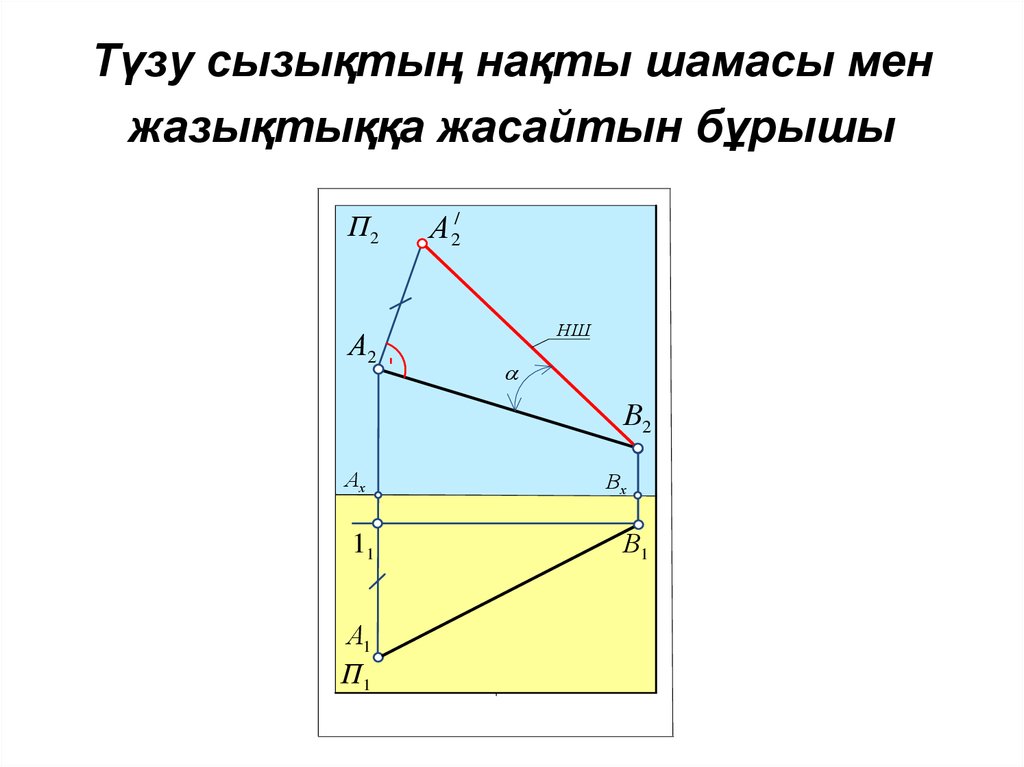
11. Түзу сызықтың нақты шамасы мен жазықтыққа жасайтын бұрышы

П2
А2
А 2/
НШ
В2
Ах
11
А1
П1
Вх
В1

12. Нүкте мен жазықтықтың ара қашықтығы

С2
П2
D2
D2
12 3 2
h2
НШ
А2
f2
К2
В2
42 52
Ах
22
Сх
Вх
С1
f1
11
h1
А1
П1
В1
51
E1
К1
41 21 31
D1
В1
Р1
/