Похожие презентации:
Движение заряженных частиц в электрическом и магнитном полях
1. Лекция № 8
ДВИЖЕНИЕЗАРЯЖЕННЫХ ЧАСТИЦ
В ЭЛЕКТРИЧЕСКОМ И
МАГНИТНОМ ПОЛЯХ
2. Сила Лоренца
Из опыта: сила, действующая наточечный заряд q, зависит в общем случае и
от местоположения заряда и от его скорости v .
Обобщенная сила Лоренца – полная
электромагнитная (э/м) сила, действующая
на заряд q:
F qE q v, B
(8.1)
(8.1) – справедливо как для постоянных, так и
для переменных электрических
и магнитных
v заряда.
полей при любых
3.
Электрическая составляющая э/м силы(8.1) не зависит от
v
Магнитная сила Лоренца
FM q v, B
FM v,
FЭ qE.
(8.2)
• всегда
• сообщает частице нормальное ускорение,
изменяя ее скорость только по направлению;
• не совершает работы над заряженными
0,
A
т.к.
частицами FM
FM v
Частица в магнитном поле кинетическую
энергию не меняет.
4. Движение заряженной частицы в электрических и магнитных полях
Уравнение движения :2
d r
d r
m 2 qE q , B ,
d t
d
t
н . у . : r 0 , d r 0 .
dt
d r
a
2
dt
2
– ускорение движущейся
заряженной частицы.
Рассмотрим частные случаи.
5. Движение заряженной частицы в поперечном однородном магнитном поле
B constFM q v, B q v B
+q, m
FM
O
a
R
2
Ускорение
нерелятивистской частицы
v
FM q
a
v B
m m
При
qvB
a
m
v B
(8.3)
6.
FM v ,v2 q v B
a an
,
R
m
изменяет скорость только
по направлению.
частица движется с
FM
Под действием
v v const по окружности радиуса
Т.к.
mv
const
R
qB
Период обращения
частота
2 R 2 m
T
,
qB
v
1
qB
T
2 m
(8.4)
(8.5)
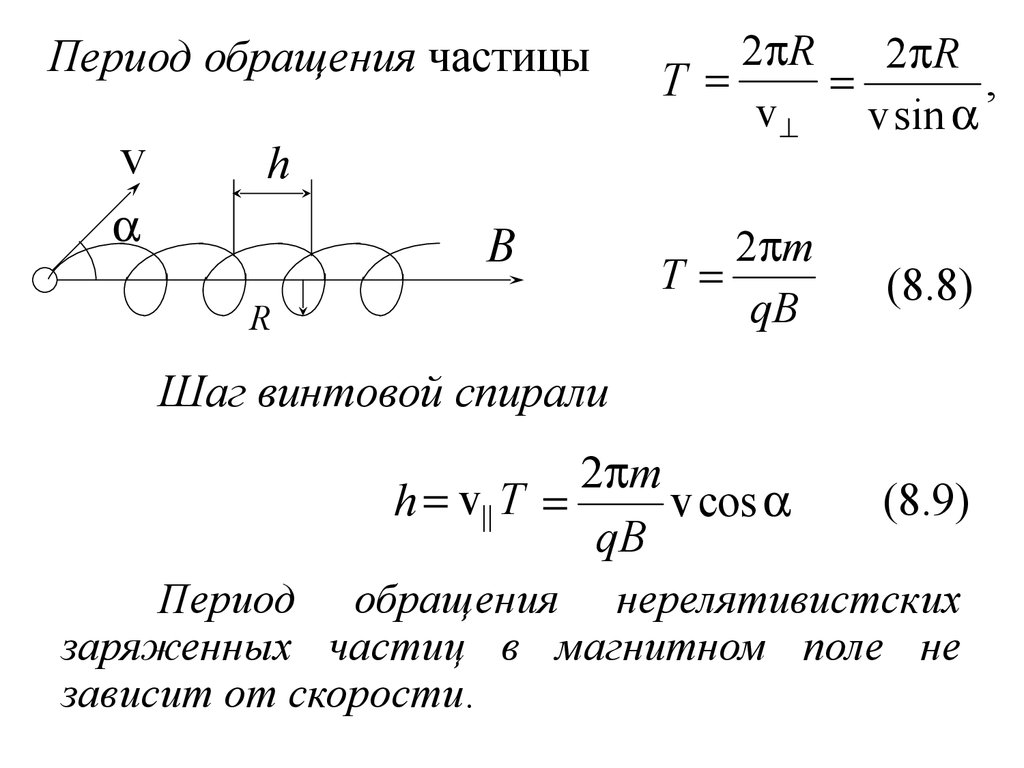
7. Движение нерелятивистской заряженной частицы в однородном непоперечном магнитном поле
B constПусть
v, B
v||
+q, m
v v|| v ,
v
где
v
v|| || B,
v B
Тогда
FM q v B q v|| B q v B q v B
8.
Здесьа
v|| B 0,
v v sin ,
v|| v cos
Это движение можно разложить на два –
вращение по окружности и поступательное
движение вдоль поля. Частица движется по
винтовой спирали с ускорением
FM
a
,
m
9.
FM q v B q v B sina
m
m
m
Поскольку
FM v ,
a an , а его величина
2
v
q v B
an
a
R
m
Радиус обращения частицы
m v m v sin
R
qB
qB
(8.7)
10.
Период обращения частицыv
h
B
R
2 R
2 R
,
T
v
v sin
2 m
T
qB
(8.8)
Шаг винтовой спирали
2 m
h v|| T
v cos
qB
(8.9)
Период обращения нерелятивистских
заряженных частиц в магнитном поле не
зависит от скорости.
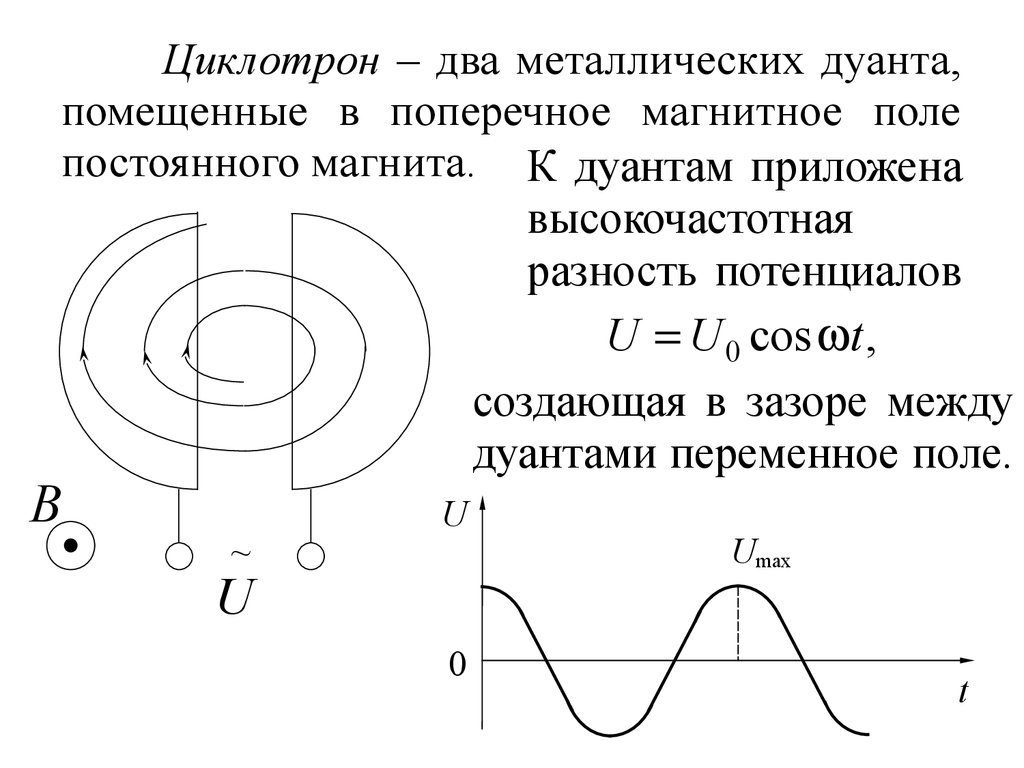
11. Ускорение заряженных частиц
Циклотрон–
предварительный
ускоритель
«+»
заряженных
частиц
(протонов, α-частиц и т.д.).
Используют независимость периода
обращения нерелятивистской частицы от
скорости (8.5), (8.8):
2 m
T
qB
12.
Циклотрон – два металлических дуанта,помещенные в поперечное магнитное поле
постоянного магнита. К дуантам приложена
высокочастотная
разность потенциалов
B
U U 0 cos t ,
создающая в зазоре между
дуантами переменное поле.
~
U
U
0
Umax
t
13.
Ионы, вылетевшие из ионного источника(помещается
в
зазоре),
ускоряются
электрическим полем. Пройдя зазор, ионы
будут двигаться в магнитном поле по
окружности. Через время
m
t
qB
ионы вновь подойдут к зазору. Если за это
время полярность дуантов поменялась, то
ионы опять будут ускоряться.
T времени
T v ,
Т.к.
в магнитном
то через
каждыйполе
интервал
Δt
ион будет попадать в зазор.
14.
Ионы будут ускоряться внешнимвысокочастотным электрическим полем,
если частота его изменения совпадает с
частотой обращения частицы (ионов) по
окружности
2 qB
2
T
m
– условие циклотронного резонанса.
Энергия, которую набирает ион
m0 v 2
qU
Wk
2
15.
Внутри дуантов действует поперечноемагнитное поле. Между – электрическое поле
U ~ 10 B, Wk ~ 25 28 МэВ (для протона).
5
1эВ= 1,6 10-19 Кл 1В = 1,6 10-19 Дж.
Дальнейшее
увеличение
энергии
практически невозможно, как в связи с
трудностями по увеличению радиуса дуантов,
так и потому, что при этом увеличивается
релятивистская масса иона
m0
m v
1 v2 c2
16.
и период его обращения также увеличивается2 m v
T v
,
qB
ион начинает выходить из резонанса и может
попадать в зазор в моменты, когда поле будет
тормозить ион.
При скоростях частиц v ~ c
для ускорения используют синхротроны (в
них – изменение магнитной индукции) и
фазотроны (синхроциклотроны) (в них
изменяется
период
высокочастотного
ускоряющего поля).
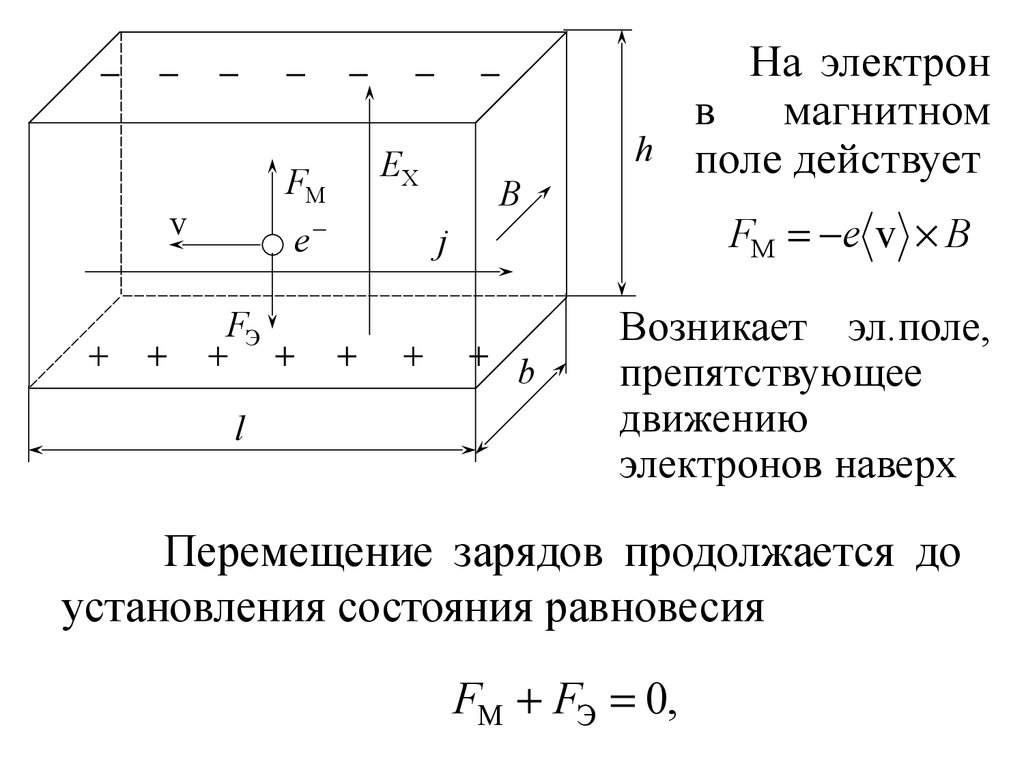
17. Эффект Холла
Припомещении
металлической
пластинки, по которой течет ток, в магнитное
поле, силовые линии которого току, между
нижней и верхней гранями пластинки
возникает
разность
потенциалов
Δφ,
называемая холловской.
Появление Δφ объясняется действием
силы Лоренца на носители тока.
18.
je
FЭ
l
EX
FM
v
B
b
На электрон
в
магнитном
h поле действует
FM e v B
Возникает эл.поле,
препятствующее
движению
электронов наверх
Перемещение зарядов продолжается до
установления состояния равновесия
FM FЭ 0,
19.
после чего накоплениезаряда прекратится и
установится значение E X
e v B eEX ,
Условие равновесия
откуда
j B
RX j B
EX v B
ene
Здесь
(8.10)
j nee v ,
где
ne
концентрация
электронов,
1
постоянная Холла
RX
ene
20.
Часто знак «–» в (8.10) относят кпостоянной Холла, т.е. для электронов RX < 0,
а для q > 0
–
RX > 0.
E X h
Холловская разность потенциалов
RX jhB
(8.11)
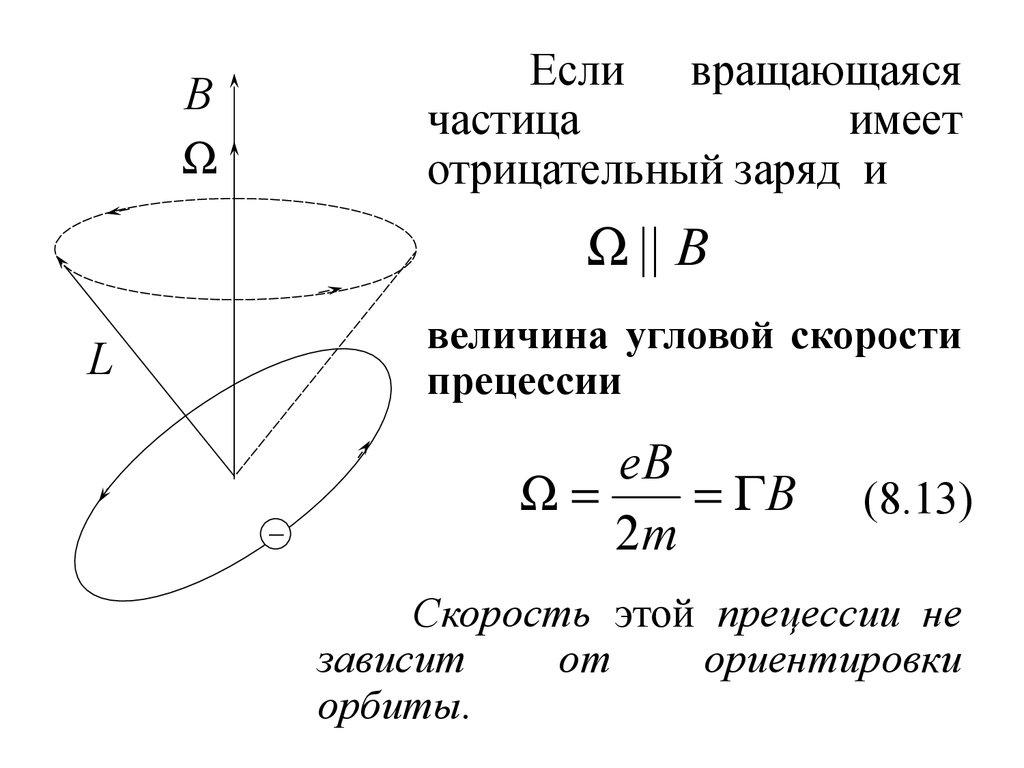
21. Ларморова прецессия электронных орбит
Движение электрона по круговой орбитеэквивалентно электрическому току
I e
где ν частота обращения электрона вокруг
ядра.
Орбитальный магнитный момент электрона
pm IS e S e r 2 ,
момент импульса и угловая скорость
L m r
2
и
2
22.
pmr
L
e
v
2
e
e
S
pm
e r
2
2
2m
L
m r
m2 r
L pm ,
поскольку
23. гиромагнитное отношение
epm
2m
L
Формула (8.12)
эллиптических орбит.
справедлива
(8.12)
и
для
Если на электрон, вращающийся по
орбите, будет действовать внешнее магнитное
поле, то на замкнутый ток в магнитном поле
действует пара сил под действием которой он
будет совершать прецессионное движение.
24.
BL
Если вращающаяся
частица
имеет
отрицательный заряд и
|| B
величина угловой скорости
прецессии
eB
B
2m
(8.13)
Скорость этой прецессии не
зависит
от
ориентировки
орбиты.
25.
ТеоремаЛармора:
действие
магнитного поля на движущийся электрон
заключается в наложении на первоначальное
движение равномерного вращения вокруг
направления внешнего магнитного поля.
Внешнее магнитное поле не вызывает
непосредственно
переориентировки
электронных орбит, но только их прецессию.
Доказательство теоремы Лармора.
Пусть в отсутствии внешнего магнитного
поля на заряженную частицу
действует
центральная сила (Кулона) F r
26.
Уравнение движения частицыd r
m 2 F r
dt
2
(8.14)
Включили внешнее
магнитное поле с
и ввели новую систему
индукцией B
координат, которая равномерно
вращается с
угловой скоростью || B
Во вращающейся системе на частицу
будут действовать: магнитная сила Лоренца
FM e v, B
27.
сила КориолисаFK 2m v,
и центробежная сила
2
Fц m r
Для достаточно малого Ω
Fц FK
Так как || B, то при должном
величины Ω можно получить
FM FK 0
выборе
28.
Это выполняется, еслиe v B sin v, B 2m v sin v, B 0
или
eB
2m
В рассматриваемой вращающейся системе
координат уравнение движения частицы
будет иметь прежний вид (8.14).
29.
Действие магнитного поля в первомприближении (пока можно пренебречь
центробежной силой) сводится к наложению
дополнительного равномерного вращения с
угловой скоростью Ω. Для электрона
получаем формулу (8.13).
Прецессионный
всегда
магнитный
p m B
p m p m
момент

























 Физика
Физика








