Показательные неравенства

1. Показательные неравенства Решение показательных неравенств основано на свойствах показательной функции.

2. График показательной функции y = ах, а ≠ 1, a > 0

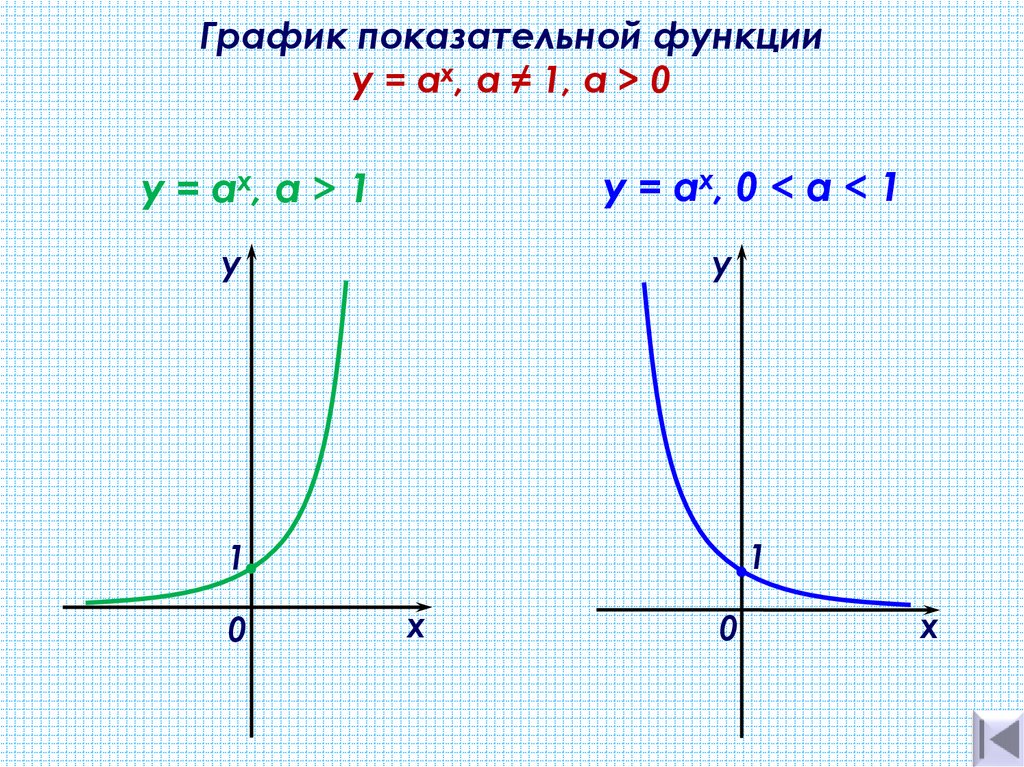
График показательной функции
y = ах, а ≠ 1, a > 0
y = ах, 0 < а < 1
y = ах, а > 1
у
у
1
1
0
х
0
х

3. Свойства сравнения выражений вида ах, а ≠ 1, a > 0

Свойства сравнения выражений вида ах, а ≠ 1, a > 0
1.
Если 0 < а < 1 или а > 1, то равенство ar = as справедливо
тогда и только тогда, когда r = s.
2.
Если 0 < а < 1, то
a) неравенство ax > 1 справедливо ⟺ x < 0;
б) неравенство ax < 1 справедливо ⟺ x > 0.
3.
Если а > 1, то
a) неравенство ax > 1 справедливо ⟺ x > 0;
б) неравенство ax < 1 справедливо ⟺ x < 0.
4.
Если а > 1, то
a) неравенство af(x) > ah(x) справедливо ⟺ f(x) > h(x);
б) неравенство af(x) < ah(x) справедливо ⟺ f(x) < h(x).
5.
Если 0 < а < 1, то
a) неравенство af(x) > ah(x) справедливо ⟺ f(x) < h(x);
б) неравенство af(x) < ah(x) справедливо ⟺ f(x) > h(x).

4. Показательные неравенства

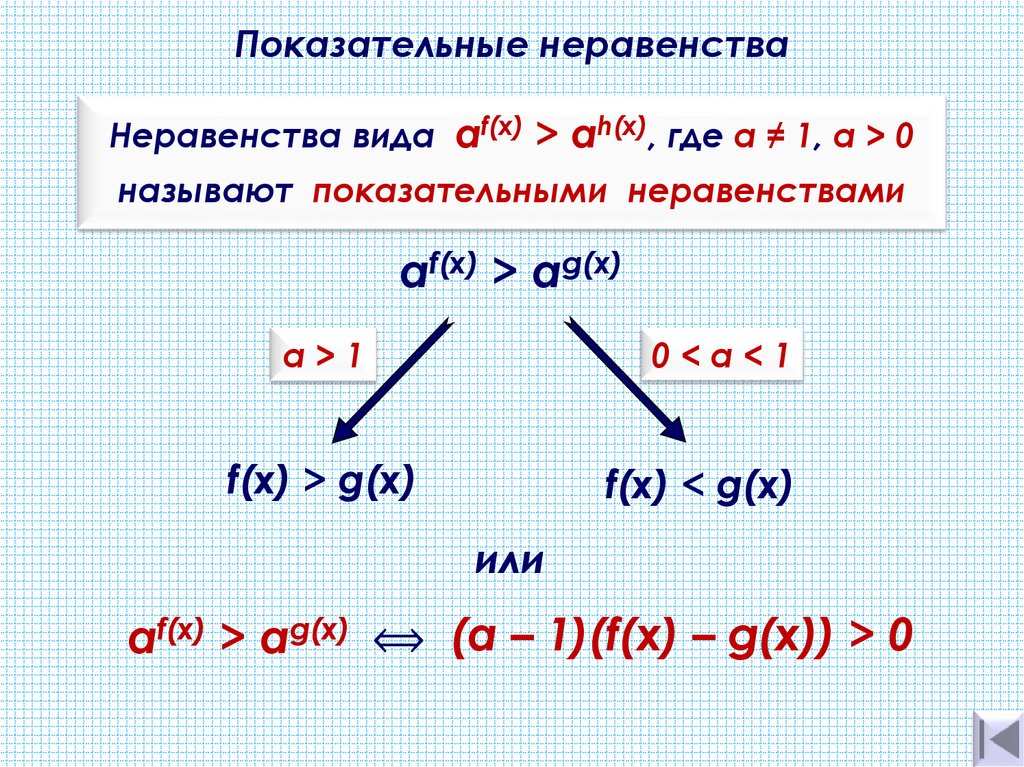
Неравенства вида af(x) > аh(х), где а ≠ 1, a > 0
называют показательными неравенствами
af(x) > аg(х)
а>1
0<а<1
f(x) > g(х)
f(x) < g(х)
или
af(x) > аg(х) ⟺ (а – 1)(f(x) – g(x)) > 0

5. Показательные неравенства. Примеры

Пример 1
22 x 4 64
22 x 4 26
т.к . функция у 2t монотонно
возрастает на R , то
2x 4 6
x 5
Ответ : 5;
Пример 2
1
3
2 x 3 ,5
1
3
2 x 3 ,5
1
3
1
3
0 ,5
t
1
т.к . функция у
3
монотонно убывает на R , то
2x 3 ,5 0 ,5
x 2
Ответ : 2;

6. Показательные неравенства. Примеры

Пример 3
0,5
x 2 3 x
0,53 x 8
т.к. функция у 0,5 t
монотонно убывает на R, то
x 2 3x 3x 8
x2 6x 8 0
x2 6x 8 0
x1 2,
x 4
2
х ; 2 4;
Ответ : ; 2 4;
−
+
2
+
4
х

7. Показательные неравенства. Примеры

Пример 4
8 x 18 х 2 27 x
23 x 2х 32x 2 33 x
: 33 х , т.к . 33 х 0
23 x 2х 32x 2 33 x
3х
3х
3
3
33 х
2
3
3x
x
2
2
3
x
2
Пусть t , где t 0
3
t3 t 2 0
t 3 t 2 t 3 t 1 1 t 3 1 t 1 t 1 t 2 t 2
т.к . t 2 t 2 0 для любых t , то t 1 0
t 1

8. Показательные неравенства. Примеры

Пример 4 (продолжение)
Вернемся к исходной переменной :
x
2
1
3
x
0
2 2
,
3 3
x
т.к. а
2
2
1, то функция у убывает на R
3
3
x 0
Ответ : ; 0 .