Похожие презентации:
Also known as Hysterical Calculus
1.
Calculus++ Light2.
Question 1. A sequence an, n = 1,2,3,…,satisfies lim (2n 1)an 16 .
n
a) Use the definition of limit to obtain a
sandwich inequality for an.
Solution: Since the limit of (2n – 1) an is 16 we
have: 0, N , n N : | (2n 1)an 16 | .
Set 1, then | (2n 1)an 16 | 1, n N .
That is, 1 (2n 1)an 16 1
15 (2n 1)an 17
15
17
an
lim an 0.
n
2n 1
2n 1
3.
b) Conclude that lim an 0,n
and find lim nan .
n
We have nan 12 (2n 1)an 12 an
Therefore
lim nan lim 12 (2n 1)an lim 12 an
n
n
n
12 lim (2n 1)an 12 lim an
n
12 16 12 0 8.
n
4.
Calculus++Also known as
Hysterical Calculus
5.
Question 2. A sequence xn, n = 1,2,3,… isxn 1 xn 2
defined by the relationship xn
2
and the initial conditions x1 = a, x2 = b.
Find lim xn .
n
Solution. We begin with finding an explicit
expression for the general term of the
sequence xn.
n
Let us try the following formula: xn c .
xn 1 xn 2
n
n 1
n 2
1
1
xn
c 2 c 2 c .
2
2
n 2
Divide both sides by c to obtain 12 12 ,
2
or 12 12 0 1 1, 2 12 .
6.
Thus, we found two sequences that satisfy thexn 1 xn 2
defining relationship xn
:
2
( 2)
(1)
1 n
xn c1 and xn c2 ( 2 ) .
Do any of these sequences satisfy the initial
conditions x1 = a, x2 = b?
Well, if a = b, then the first sequence with c1 = a,
(1)
xn a, satisfies the initial conditions.
If b = – ½ a, then the second sequence with
c2 = –2 a, xn( 2 ) a ( 12 ) n 1 , satisfies the initial
conditions.
But what should we do if a and b are arbitrary?
7.
Well, we can consider linear combination of1 n
the two obtained sequences xn c1 c2 ( 2 ) .
Let us check that this linear combination
xn 1 xn 2
.
indeed satisfies the equation xn
2
We have
1 n 1
2
xn 1 xn 2 c1 c2 ( )
2
1 n 2
2
c1 c2 ( )
2
1 1
1 2
( 2 ) ( 2 )
1 n
c1 c2 ( 2 )
2
1 n
c1 c2 ( 2 ) xn .
8.
Now all we have to do is to find the values ofc1 and c2 such that our sequence also
satisfies the initial conditions:
x1 c1 c2 ( 12 ) a,
1
x2 c1 4 c2 b.
For the values of arbitrary constants c1 and c2
we obtain 3c1 a 2 b , 43 c2 b a.
a 2b 4
1 n
Thus xn
( b a )( 2 ) .
3
3
Now the limit n is not difficult to find:
1
2
lim xn 3 a 3 b.
n
9. The method of the week
To find the sequence that satisfies the definingrelationship xn xn 1 xn 2 ,
and the initial conditions x1 = a, x2 = b we
have to:
1. Write down the characteristic equation
0
and obtain its roots 1 , 2 .
2
2. Write down the general formula for xn:
xn c c ,
n
1 1
n
2 2
and find the values of constants c1 and c2,
such that x1 = a, x2 = b.
10.
Question 3 a). Find the following limitSolution: We have
sin n 1 sin n 1 n n
sin n 1 n cos( n )
cos n 1 n sin( n )
0
sin n 1 n ( 1) .
lim sin n 1 .
2
n
2
2
2
2
2
n
11.
n 1 n2
2
2
n 1 n
n 1 n
2
n 1 n
2
2
n 1 n
n 1 n
1
.
2
n 1 n
2
We have
The obtained identity yields
sin n 1 sin n 1 n ( 1)
2
2
n
sin
(
1
)
.
2
n 1 n
n
12.
Therefore we can use the following sandwichinequality
2
sin
sin
n
1
2
n 1 n
.
sin
2
n 1 n
Since sin x is a continuous function we obtain
sin lim
lim sin
n 2
2
n
n 1 n
n 1 n
sin 0 0 .
Hence, the sandwich theorem tells us that
lim sin n 1 0 .
n
2
13.
Question 4. State a (positive) definition of adivergent sequence {xn}.
Solution: We begin with the definition of a
convergent sequence.
A sequence {xn} converges to a number L, if
0, N , n N : | x n L | .
A sequence {xn} does not converges to a
number L, if
0, N , n N : | x n L | .
A sequence {xn} is divergent, if it does not
converges to any number L.
L, 0, N , n N : | xn L | .
14.
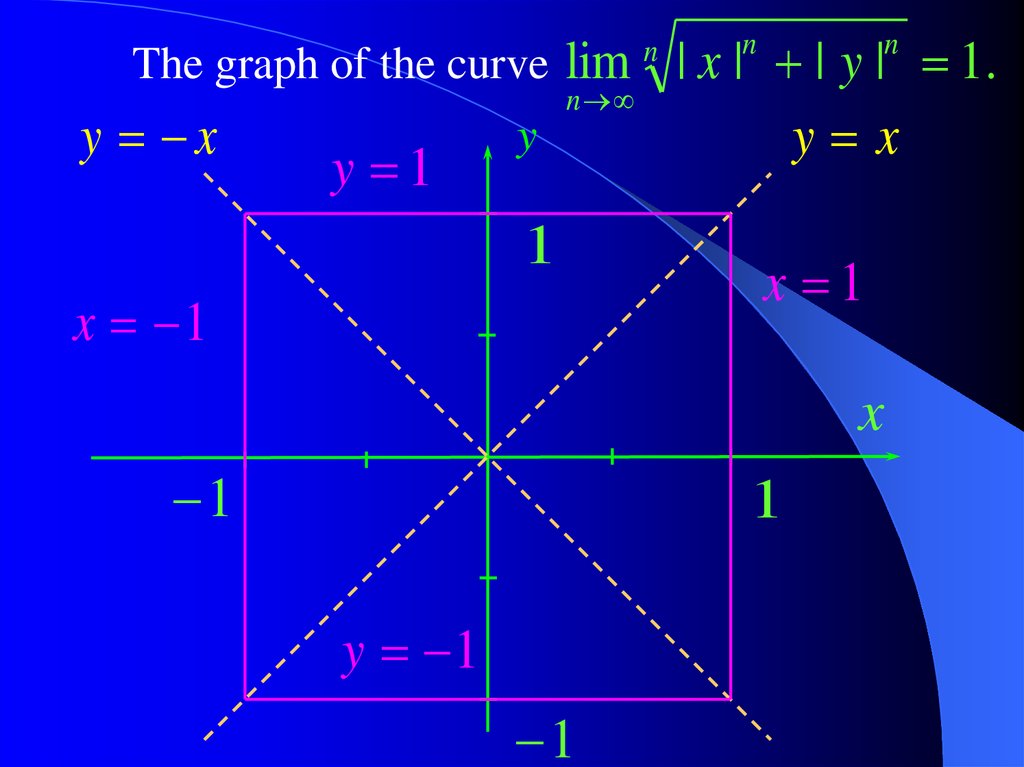
Question 5. Draw the curve defined by then
n
n
equation lim | x | | y | 1
n
in the x y – plane.
Solution. To begin with, we calculate the limit
lim | x | | y | ,
n
n
n
n
in the particular case x = – 7, y = 5.
We have | 7 |n | 7 |n | 5 |n 2 | 7 |n .
| 7 | | 7 | | 5 | 2 | 7 | .
Since lim n 2 1, the sandwich theorem
n
n
n
n
tells us that lim | 7 | | 5 | | 7 | 7 .
Hence,
n
n
n
n
n
15.
Now we can find the limit limn
n
|x| |y| .
n
n
Note the following double inequality
max(| x |, | y |)
Hence
n
|x| |y|
n
2 max(| x |, | y |) .
n
n
max(| x |, | y |) | x | | y |
n
n
n
2 max(| x |, | y |).
n
16.
Since lim 2 1, the sandwich theoremn
n
tells us that
lim | x | | y | max(| x |, | y |).
n
n
n
n
Thus, we have to draw the curve defined by
the equation
max(| x |, | y |) 1 .
17.
Let us look at the xy – plane:y x
max(| x |, | y |) y
y
y 1
1
x 1
max(| x |, | y |) x
y x
x 1
max(| x |, | y |) x
x
1
1
y 1 1
max(| x |, | y |) y
18.
The graph of the curve limy x
n
y 1
y
1
x 1
n
| x | | y | 1.
y x
n
n
x 1
x
1
1
y 1
1
19.
Question 6. Use the definition of convergentsequence to obtain a sandwich inequality
for the sequence
n
1007 sin n
xn
, n 1,2,3,...,
n
1008
and find the limit of this sequence.
sin n
Solution: The sequence y n
n
converges to 0.
Therefore, according to the definition of the
limit, 0, N , n N : | y n 0 | .
1
and denote N1 – the
Choose
2016 corresponding value of N.
20.
The definition tells us that1
sin n
1
for all n N 1 .
2016
n
2016
1007
1
1007 sin n 1007
1
1008 2016 1008
n
1008 2016
2013 1007 sin n 2015
2016 1008
n
2016
Therefore we obtain the following sandwich
inequality for our sequence xn
n
n
n
0
2013 1007 sin n 2015
n 2016
2016 1008
0
for all n N 1 .
21.
Now the sandwich theorem tells us thatn
1007 sin n
lim
0.
n 1008
n




















 Математика
Математика








