Functions of Random Variables 2. Method of Distribution Functions

1. Functions of Random Variables

2. Method of Distribution Functions

X1,…,Xn ~ f(x1,…,xn)
U=g(X1,…,Xn) – Want to obtain fU(u)
Find values in (x1,…,xn) space where U=u
Find region where U≤u
Obtain FU(u)=P(U≤u) by integrating
f(x1,…,xn) over the region where U≤u
• fU(u) = dFU(u)/du

3. Example – Uniform X

• Stores located on a linear city with density
f(x)=0.05 -10 ≤ x ≤ 10, 0 otherwise
• Courier incurs a cost of U=16X2 when she delivers to a
store located at X (her office is located at 0)
U u 16 X 2 u
U u
X
u
4
u
u
X
4
4
FU (u ) P(U u )
u
u
u
0.05dx 0.05
4
4 4 40
u 4
u
dFU (u ) u 1/ 2
fU (u )
du
80
0 u 1600
0 u 1600

4. Example – Sum of Exponentials

X1, X2 independent Exponential(q)
f(xi)=q-1e-xi/q xi>0, q>0, i=1,2
f(x1,x2)= q-2e-(x1+x2)/q x1,x2>0
U=X1+X2
U u X 1 X 2 u X 1 u x2
U u X 1 X 2 u X 2 u, X 1 u X 2
P (U u )
u
0
u
1
0
q
e
x2 / q
q
u / q
ue
2
0
1 e
1 e u / q
1
u x2
1
q
1
q
2
e
x1 / q
( u x2 ) / q
e
x2 / q
ue u / q
2
1
0
q
dx1dx2
dx q e
u
u
1
x2 / q
0
fU (u )
e
x2 / q
u
1
0
q
dx2
e
x1 / q
u x2
0
dx2
e ( x2 u x2 ) / q dx2
1
u
e u / q e u / q 2 e u / q
q
q
q
1
u 0 U ~ Gamma( 2, q )

5. Method of Transformations

• X~fX(x)
• U=h(X) is either increasing or decreasing in X
• fU(u) = fX(x)|dx/du| where x=h-1(u)
• Can be extended to functions of more than one random variable:
• U1=h1(X1,X2), U2=h2(X1,X2), X1=h1-1(U1,U2), X2=h2-1(U1,U2)
dX 1
dU1
| J |
dX 2
dU1
dX 1
dU 2 dX 1 dX 2 dX 1 dX 2
dX 2 dU1 dU 2 dU 2 dU1
dU 2
f (u1 , u2 ) f ( x1 , x2 ) | J |
fU1 (u1 ) f (u1 , u2 )du2

6. Example

fX(x) = 2x 0≤ x ≤ 1, 0 otherwise
U=10+500X (increasing in x)
x=(u-10)/500
fX(x) = 2x = 2(u-10)/500 = (u-10)/250
dx/du = d((u-10)/500)/du = 1/500
fU(u) = [(u-10)/250]|1/500| = (u-10)/125000
10 ≤ u ≤ 510, 0 otherwise

7. Method of Conditioning

• U=h(X1,X2)
• Find f(u|x2) by transformations (Fixing X2=x2)
• Obtain the joint density of U, X2:
• f(u,x2) = f(u|x2)f(x2)
• Obtain the marginal distribution of U by
integrating joint density over X2
fU (u) f (u | x2 ) f ( x2 )dx2

8. Example (Problem 6.11)

• X1~Beta( 2, 2 X2~Beta( 3, 1 Independent
• U=X1X2
• Fix X2=x2 and get f(u|x2)
f ( x1 ) 6 x1 (1 x1 ) 0 x1 1
U X 1 x2 X 1 U / x2
f (u | x2 ) 6(u / x2 )(1 u / x2 )
f ( x2 ) 3 x22 0 x2 1
dX 1
1 / x2
dU
1
x2
0 u x2
f (u , x2 ) f (u | x2 ) f ( x2 ) 6(u / x2 )(1 u / x2 )
1 2
u
3 x2 18u 1 0 u x2 1
x2
x2
1
18u 2
dx2 18ux2 18u 2 ln( x2 ) 18u 0 18u 2 18u 2 ln( u )
fU (u ) f (u | x2 ) f ( x2 )dx2 18u
u
u
u
x2
18u (1 u u ln( u )) 0 u 1
1
1

9.

Problem 6.11
7
6
Density of U=X1X2
5
4
f(u)
f(u|x2=.25)
f(u|x2=.5)
f(u|x2=.75)
3
2
1
0
0
0.1
0.2
0.3
0.4
0.5
u
0.6
0.7
0.8
0.9
1

10. Method of Moment-Generating Functions

X,Y are two random variables
CDF’s: FX(x) and FY(y)
MGF’s: MX(t) and MY(t) exist and equal for |t|<h,h>0
Then the CDF’s FX(x) and FY(y) are equal
Three Properties:
– Y=aX+b MY(t)=E(etY)=E(et(aX+b))=ebtE(e(at)X)=ebtMX(at)
– X,Y independent MX+Y(t)=MX(t)MY(t)
– MX1,X2(t1,t2) = E[et1X1+t2X2] =MX1(t1)MX2(t2) if X1,X2 are indep.

11. Sum of Independent Gammas

X i ~ Gamma( i , ) i 1,..., n (independe nt)
M X i (t ) (1 t ) i
i 1,..., n
n
Y Xi
i 1
M Y (t ) E etY E e t ( X1 ... X n ) E etX1 e tX n M X1 (t ) M X n (t )
(1 t )
1
(1 t )
n
i 1 i
(1 t )
n
Y X i ~ Gamma i ,
i 1
i 1
n
n

12. Linear Function of Independent Normals

X i ~ Normal ( i , i2 ) i 1,..., n (independe nt)
i2t 2
M X i (t ) exp i t
i 1,..., n
2
n
Y ai X i {ai } fixed constants
i 1
M Y (t ) E e tY E e t ( a1 X 1 ... an X n ) E e ta1 X 1 e tan X n M X 1 (a1t ) M X n (ant )
n
n2 ant 2
12 a1t 2
exp 1a1t
exp n ant
exp i 1 ai i t
2
2
n
n
Y ai X i ~ Normal ai i , ai2 i2
i 1
i 1
i 1
n
2 2 2
a
i t
i
i 1
2
n

13. Distribution of Z2 (Z~N(0,1))

Z ~ N (0,1)
M Z 2 (t ) e
f Z ( z)
2
0
z
2 1 2 t
1 z
e
2
2 1 2 t
1 z2 / 2
1 z 2
1 z 2
e
dz
e
dz 2
e
dz (symmetric about 0)
0
2
2
2
dz
1
z u
0.5u 1/ 2 dz 0.5u 1/ 2 du
du 2 u
tz 2
Let u z 2
1 z2 / 2
e
2
2 1 2 t
2
dz
1
2
0
u
1 / 2
e
2
u /
1 2 t
du
1
2
0
u
1 / 2 1
e
2
u /
1 2 t
du
1
2 (1 2t ) 1/ 2 (1 2t ) 1/ 2
2
Z 2 ~ Gamma( 1 / 2, 2) 12
Notes :
0
y 1e y / dy ( )
(1 / 2)
n
Z1 ,..., Z n mutually independen t Z i2 ~ Gamma( n / 2, 2) n2
i 1
1
2
(1 / 2)
2
1 2t
1/ 2

14. Distributions of and S2 (Normal data)

Distributions of
X 1 ,..., X n ~ NID ( , 2 )
n
NID Normal and Independen tly Distribute d
n
i 1
Sample Mean : X
and S2 (Normal data)
X
Xi
n
n
1
X i ai X i
i 1 n
i 1
n
n
n
n
i 1
i 1
i 1
1
n
ai
i 1,..., n
Note : X i X X i n X X i X i 0
i 1
X
n
Sample Variance : S 2
i 1
X
i
2
n 1
Alternativ e representa tion of S 2 :
n
n
n
n
1
1
2
S
( X i X j ) 2n(n 1)
Xi X X j X
2n( n 1) i 1 j 1
i 1 j 1
2
X
n
n
1
Xi X
2n( n 1) i 1 j 1
2
n
1
n X i X
2n( n 1) i 1
n
1
n X i X
2n( n 1) i 1
2
2
X
j
n
2
2 Xi X X j X
n X j X
j 1
n
n X j X
j 1
2
2
2
2 X i X X j X
i 1 j 1
n
n
n
2 X i X
i 1
1
n( n 1) S 2 n( n 1) S 2 2(0)( 0)
2n( n 1)
X
n
j 1
j
2n( n 1) S 2
2n( n 1)
So S 2 is a function of the difference s of the sampled data
X
S2

15. Independence of and S2 (Normal Data)

Independence of X and S2 (Normal Data)
Independence of T=X1+X2 and D=X2-X1
for Case of n=2
X 1 , X 2 ~ NID( , 2 )
2 2t 2
2 2
T X 1 X 2 ~ N (2 ,2 ) M T (t ) exp 2 t
exp{ 2 t t }
2
2
2 2t 2
2 2
D X 2 X 1 ~ N (0,2 ) M D (t ) exp 0
exp{
t }
2
M T , D (t1 , t 2 ) E (e t1T t2 D ) E exp t1 ( X 1 X 2 ) t 2 ( X 2 X 1 )
2
E exp[ X 1 (t1 t 2 ) X 2 (t1 t 2 )]
E exp( X 1 (t1 t 2 )) exp( X 2 (t1 t 2 ))
ind
E exp( X 1 (t1 t 2 )) E exp( X 2 (t1 t 2 ))
X

16. Independence of and S2 (Normal Data) P2

Independence of X and S2 (Normal Data) P2
Independence of T=X1+X2 and D=X2-X1
for Case of n=2
E exp( X 1 (t1 t 2 )) exp( X 2 (t1 t 2 ))
ind
E exp( X 1 (t1 t 2 )) E exp( X 2 (t1 t 2 ))
2 (t1 t 2 ) 2
2 (t1 t 2 ) 2
exp (t1 t 2 )
exp (t1 t 2 )
2
2
2 (t12 t 22 2t1t 2 t12 t 22 2t1t 2 )
exp (t1 t 2 t1 t 2 )
2
2 2t12 2 2t 22
exp 2 t1
2
2
2 2t 22
2 2t12
exp
M T (t1 ) M D (t 2 )
exp 2 t1
2
2
Thus T=X1+X2 and D=X2-X1 are independent Normals and
X & S2 are independent

17. Distribution of S2 (P.1)

X i ~ NID( , 2 ) Z i
Xi
~ N (0,1) Z i2 ~ 12
X
2
i
~ n Gamma(n / 2,2)
i 1
2
n
1 n
1 n
Xi
2 X i 2 X i X X
i 1
i 1
i 1
2
2
1 n
X
X
X
2 Xi X X
i
2
2
n
i 1
2
1 n
2 X i X
i 1
1
Xi X
2
i 1
n
n
2
i 1
n X 0 (n 1)S
2
2
2
2
n X 2 X X
2
2
X
i
n X
2
2
Now, X and S 2 are independen t :
M ( n 1) S 2 n ( X ) 2 (t ) M ( n 1) S 2 (t ) M n ( X ) 2 (t ) M
2
2
2
1
2
n
2
X i
i 1
(1 2t ) n / 2

18. Distribution of S2 P.2

Now, X and S 2 are independen t :
M ( n 1) S 2 n ( X ) 2 (t ) M ( n 1) S 2 (t ) M n ( X ) 2 (t ) M
2
Now, consider :
2
n X
2
2
1
n
2
X i
(1 2t ) n / 2
2 i 1
2
:
2
n
n
X X X
1
1
2
n X
2
2
X ~ N X , X
ZX
~ N (0,1)
n
X
n
i 1 n
i 1 n
n X
2
2
~ 12 M n ( X ) 2 (t ) (1 2t ) 1/ 2
2
M
M ( n 1) S 2 (t )
2
1
2
n
X i
2 i 1
M n( X )2
(1 2t ) n / 2
(1 2t ) ( n / 2 ) (1/ 2 ) (1 2t ) ( n 1) / 2
1 / 2
(1 2t )
2
(n 1) S 2
2
n 1
~ Gamma
,2 n2 1
2

19. Summary of Results

• X1,…Xn ≡ random sample from N( , 2) population
• In practice, we observe the sample mean and sample variance (not
the population values: , 2)
• We use the sample values (and their distributions) to make
inferences about the population values
n
X
Xi
i 1
n
X
n
2
S 2
X ~ N ,
n
i 1
i X
(n 1) S 2
2
n 1
X , S 2 are independen t
t
X
S/ n
X
/
n
2
(n 1) S
(n 1)
2
Z
2
n 1
(n 1)
~ t n 1
(See derivation using method of conditioni ng on .ppt
presentati on for t, and F - distributi ons)
X
n
2
i 1
i X
2
2
~ n2 1

20. Order Statistics

• X1,X2,...,Xn Independent Continuous RV’s
• F(x)=P(X≤x) Cumulative Distribution Function
• f(x)=dF(x)/dx Probability Density Function
• Order Statistics: X(1) ≤ X(2) ≤ ...≤ X(n)
(Continuous can ignore equalities)
• X(1) = min(X1,...,Xn)
• X(n) = max(X1,...,Xn)

21. Order Statistics

CDF of Maximum X ( n ) :
P X ( n ) x P ( X 1 x,..., X n x) P X 1 x P ( X n x) [ F ( x)]n
pdf of Maximum :
g n ( x)
dP ( X ( n ) x)
dx
d [ F ( x)]n
dF ( x)
n[ F ( x)]n 1
n[ F ( x)]n 1 f ( x)
dx
dx
CDF of Minimum X (1) :
P X (1) x 1 P ( X 1 x,..., X n x) 1 P X 1 x P ( X n x) 1 [1 F ( x)]n
pdf of Minimum :
dP ( X (1) x)
d [1 [1 F ( x)]n ]
g1 ( x)
dx
dx
d [1 F ( x)]
n[1 F ( x)]n 1
n[1 F ( x)]n 1 f ( x)
dx

22. Example

• X1,...,X5 ~ iid U(0,1)
(iid=independent and identically distributed)
0 x 0
F ( x) x 0 x 1
1 x 1
1 0 x 1
f ( x)
0 o.w.
5 x 4 (1) 5 x 4
Maximum : g n ( x)
0
0 x 1
o.w.
5(1)(1 x) 4 5(1 x) 4
Minimum : g1 ( x)
0
0 x 1
o.w.

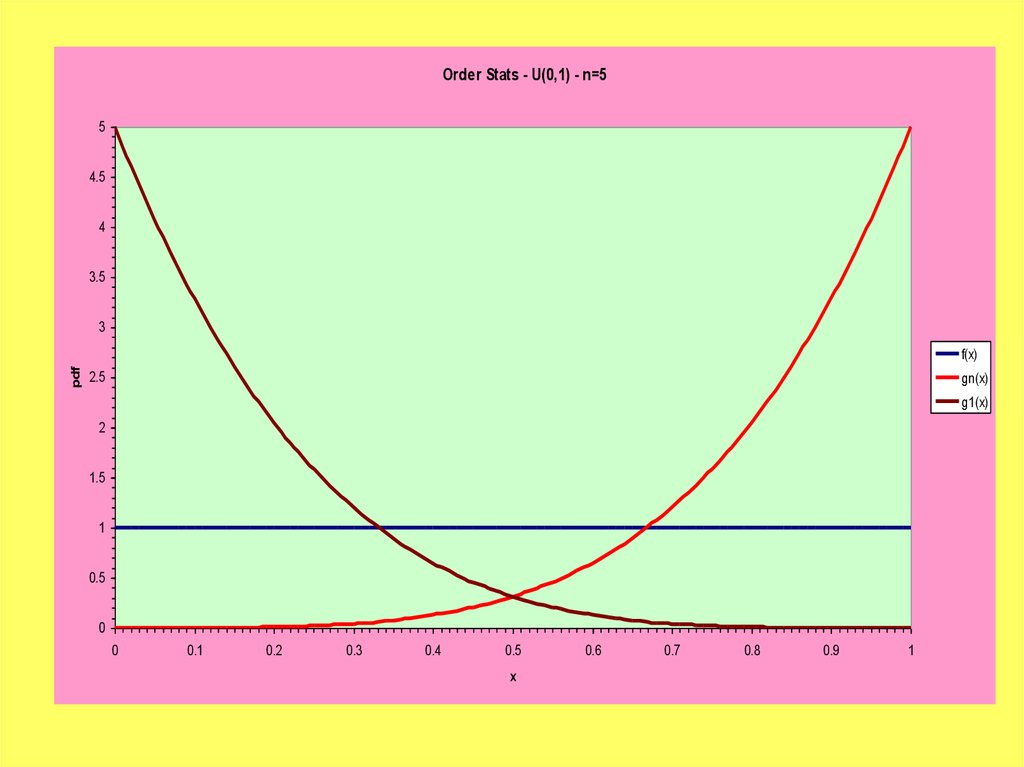
23.

Order Stats - U(0,1) - n=5
5
4.5
4
3.5
3
pdf
f(x)
2.5
gn(x)
g1(x)
2
1.5
1
0.5
0
0
0.1
0.2
0.3
0.4
0.5
x
0.6
0.7
0.8
0.9
1

24. Distributions of Order Statistics

• Consider case with n=4
• X(1) ≤x can be one of the following cases:
Exactly one less than x
Exactly two are less than x
Exactly three are less than x
All four are less than x
• X(3) ≤x can be one of the following cases:
• Exactly three are less than x
• All four are less than x
• Modeled as Binomial, n trials, p=F(x)

25. Case with n=4

4
4
1
3
P X (1) x [ F ( x)] [1 F ( x)] [ F ( x)]2 [1 F ( x)]2
1
2
4
4
3
[ F ( x)] [1 F ( x)] [ F ( x)]4 [1 F ( x)]0
3
4
1 [1 F ( x)]4
4
4
3
P X ( 3) x [ F ( x)] [1 F ( x)] [ F ( x)]4 [1 F ( x)]0
3
4
4 F ( x) 3 4 F ( x) 4 F ( x) 4
4 F ( x ) 3 3F ( x ) 4
g 3 ( x) 12 F ( x) 2 f ( x) 12 F ( x) 3 f ( x) 12 f ( x) F ( x) 2 (1 F ( x))

26. General Case (Sample of size n)

g j ( x)
n!
[ F ( x)] j 1[1 F ( x)]n j f ( x) 1 j n
( j 1)!(n j )!
Joint distributi on of i th and j th order stats (uses multinomia l)
1 i j n : g ij ( xi , x j )
n!
[ F ( xi )]i 1[ F ( x j ) F ( xi )] j i 1[1 F ( x j )]n j f ( xi ) f ( x j )
(i 1)!( j i 1)!(n j )!
Joint distributi on of all order statistics :
n! f ( x1 )... f ( xn ) x1 ... xn
g12,..., n ( x1 ,..., xn )
elsewhere
0

27. Example – n=5 – Uniform(0,1)

f ( x) 1 F ( x) x 0 x 1
5!
j 1 : g1 ( x)
[ x]1 1[1 x]5 1 (1) 5(1 x) 4
0!4!
5! 2 1
j 2 : g 2 ( x)
[ x] [1 x]5 2 (1) 20 x(1 x) 3
1!3!
5!
j 3 : g 3 ( x)
[ x]3 1[1 x]5 3 (1) 30 x 2 (1 x) 2
2!2!
5! 4 1
j 4 : g 4 ( x)
[ x] [1 x]5 4 (1) 20 x 3 (1 x)
3!1!
5!
j 5 : g 5 ( x)
[ x]5 1[1 x]5 5 (1) 5 x 4
4!0!
i 1, j 5 : g15 ( x1 , x5 ) 20( x5 x1 ) 3
0 x1 x5 1

28.

Distributions of all Order Stats - n=5 - U(0,1)
5
4.5
4
3.5
f(x)
3
pdf
g1(x)
g2(x)
2.5
g3(x)
g4(x)
2
g5(x)
1.5
1
0.5
0
0
0.1
0.2
0.3
0.4
0.5
x
0.6
0.7
0.8
0.9
1