Задачи на построение с помощью циркуля и линейки

1. Задачи на построение с помощью циркуля и линейки

ЗАДАЧИ НА ПОСТРОЕНИЕ С
ПОМОЩЬЮ ЦИРКУЛЯ И
ЛИНЕЙКИ

2.

В геометрии выделяют задачи на построение, которые
можно решить только с помощью двух инструментов:
циркуля и линейки без масштабных делений.
Линейка позволяет провести произвольную
прямую, а также построить прямую, проходящую
через две данные точки; с помощью циркуля
можно провести окружность произвольного
радиуса, а также окружность с центром в
данной точке и радиусом, равным данному
отрезку.
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

3.

Основные
этапы
решения задачи на
построение
1 АНАЛИЗ
2. ПОСТРОЕНИЕ
3. ДОКАЗАТЕЛЬСТВО
4. ИССЛЕДОВАНИЕ
В том случае, когда при построении получаются равные фигуры,
будем считать, что задача имеет единственное решение.

4.

Условные обозначения
окр(О;г) - окружность с центром в точке О и
радиусом г
- знак угла
- знак принадлежности
- знак перпендикулярности
-
знак пересечения
- в скобках указано множество точек
пересечения
: - заменяет слова ”такой что”

5.

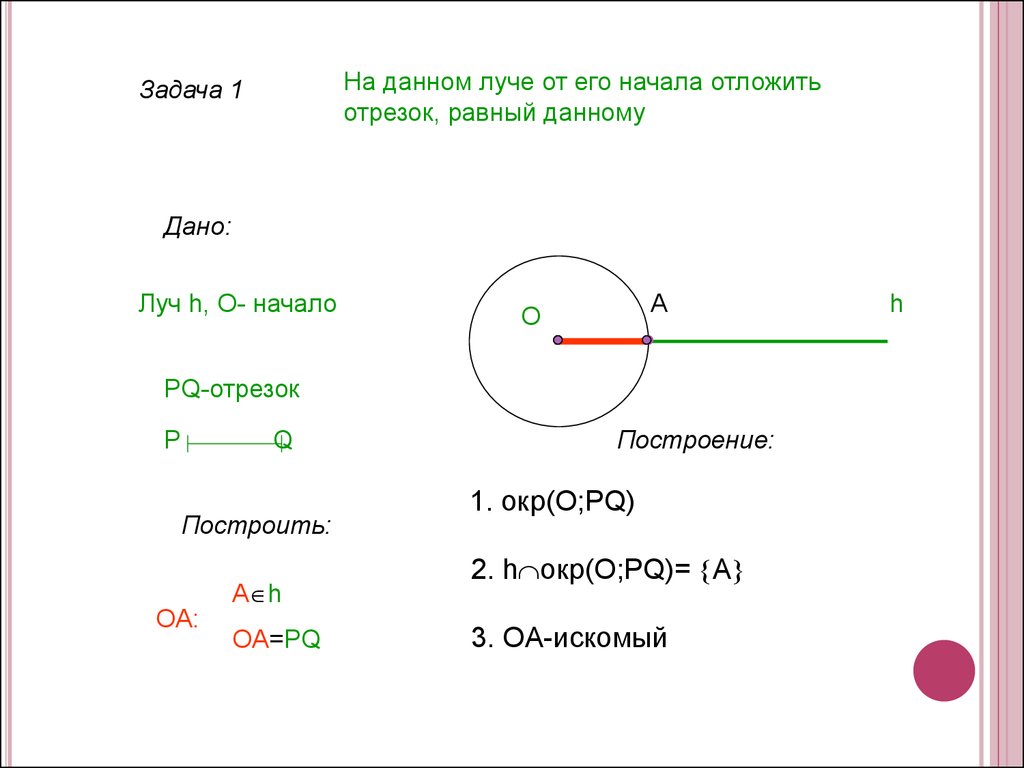
На данном луче от его начала отложить
отрезок, равный данному
Задача 1
Дано:
Луч h, О- начало
A
O
PQ-отрезок
P
Q
Построить:
A h
OA:
OA=PQ
Построение:
1. окр(О;PQ)
2. h окр(O;PQ)= A
3. OA-искомый
h

6.

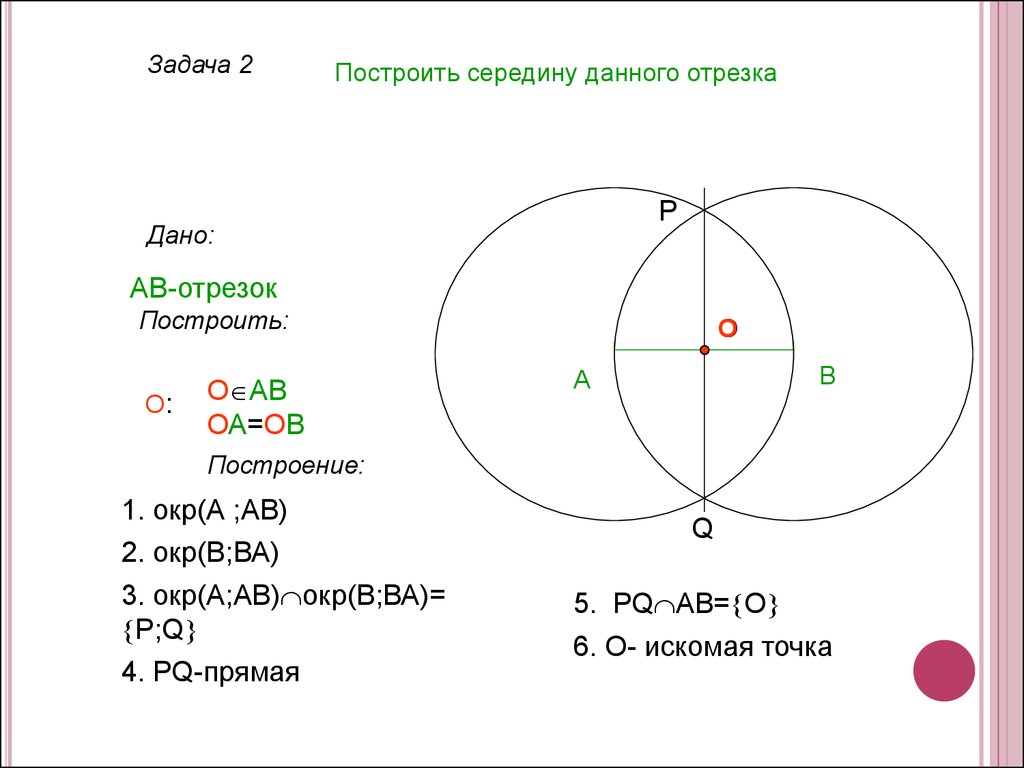
Задача 2
Построить середину данного отрезка
P
Дано:
АВ-отрезок
Построить:
О:
О АВ
ОА=ОВ
О
O
А
B
Построение:
1. окр(А ;АВ)
2. окр(В;ВА)
3. окр(А;АВ) окр(В;ВА)=
P;Q
4. PQ-прямая
Q
5. PQ AB= O
6. O- искомая точка

7.

Задача 2
Построить середину данного отрезка
P
Дано:
1 2
АВ-отрезок
Построить:
О:
О АВ
ОА=ОВ
О
А
B
Доказательство:
APQ= BPQ( по трем
сторонам)
так как 1) AP=BP=г
2) AQ=BQ=г
3) PQ-общая
Следовательно, 1= 2
Q
Значит, РО-биссектриса равнобедренного АРВ.
Значит, РО и медиана АРВ. То есть, О-середина
АВ.

8.

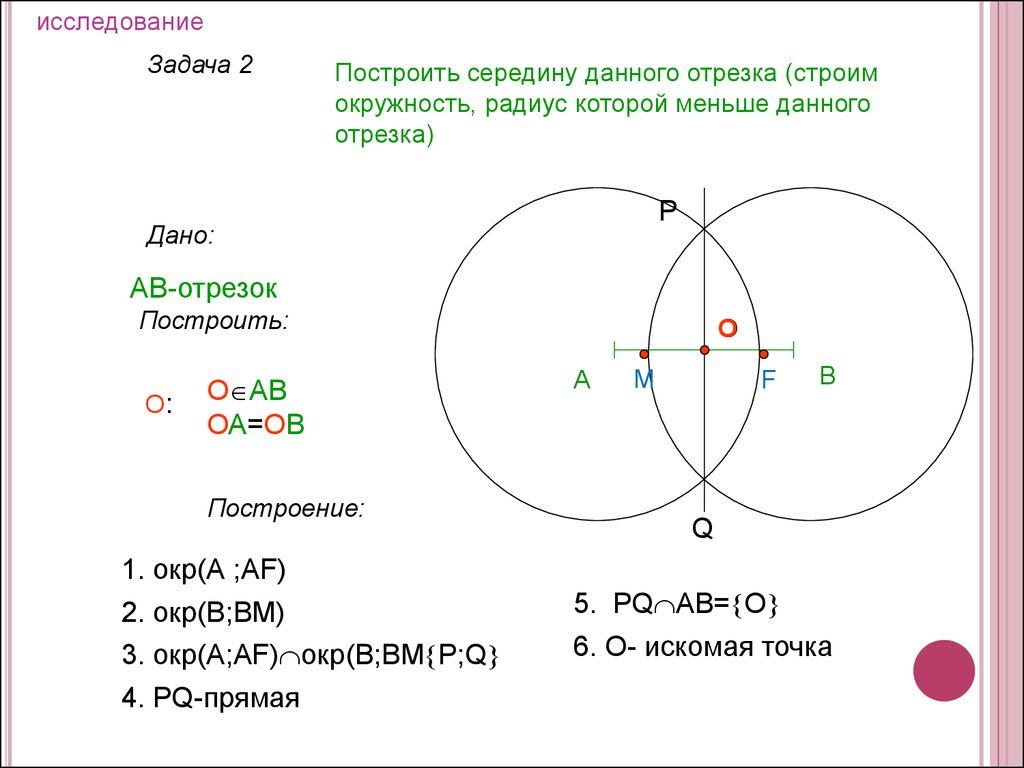
исследование
Задача 2
Построить середину данного отрезка (строим
окружность, радиус которой меньше данного
отрезка)
P
Дано:
АВ-отрезок
Построить:
О:
О АВ
ОА=ОВ
Построение:
1. окр(А ;АF)
2. окр(В;ВM)
3. окр(А;АF) окр(В;ВM P;Q
4. PQ-прямая
О
O
А
М
F
B
Q
5. PQ AB= O
6. O- искомая точка

9.

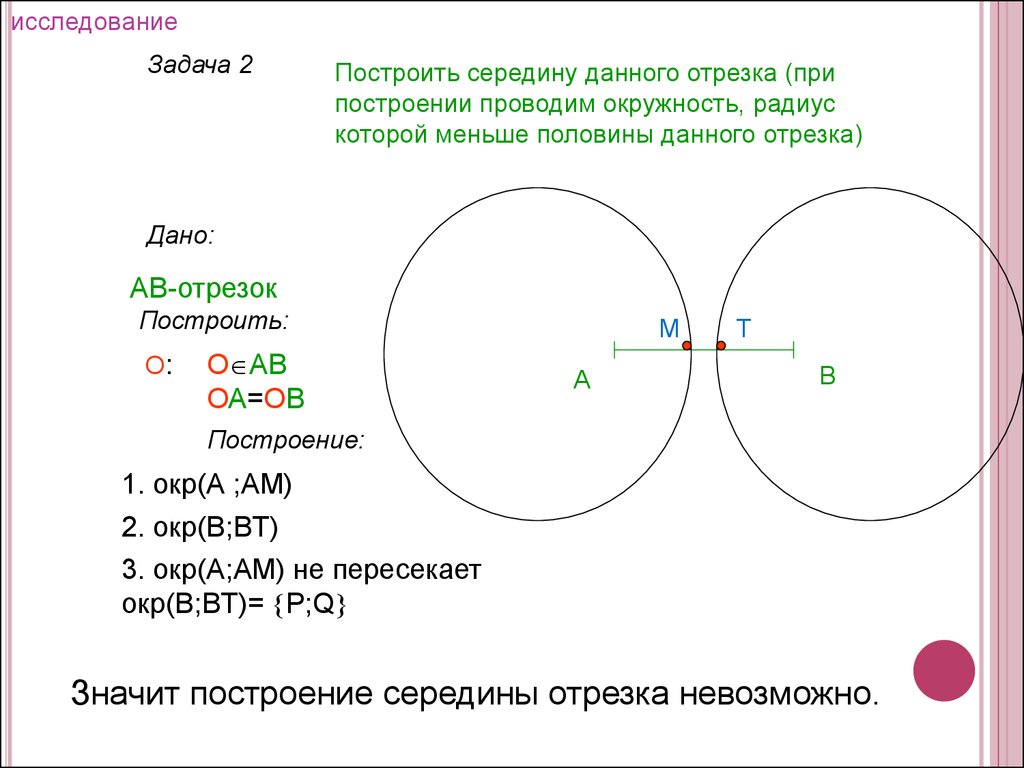
исследование
Задача 2
Построить середину данного отрезка (при
построении проводим окружность, радиус
которой меньше половины данного отрезка)
Дано:
АВ-отрезок
Построить:
О:
О АВ
ОА=ОВ
М
А
T
B
Построение:
1. окр(А ;АM)
2. окр(В;ВT)
3. окр(А;АM) не пересекает
окр(В;ВT)= P;Q
Значит построение середины отрезка невозможно.

10.

Задача 3
Построить прямую, проходящую через данную
точку и перпендикулярную к данной прямой
точка М принадлежит прямой а
Дано:
P
прямая а
точка M
М
Построить:
m:
A
M m
m a
а
m
A1
Построение:
1. окр(М;г); г-любой
2. окр(М;г) а= А;А1
3. окр(А;АА1)
7. m-искомая
Q
4. окр(А1;A1A)
5. окр(А;АА1) окр(А1;А)= P;Q
6. прямая
PQ=m

11.

Задача 4
Построить прямую, проходящую через данную
точку и перпендикулярную к данной прямой
Дано:
точка М не принадлежит прямой а
прямая а
М
точка M
Построить:
m: M m
m a
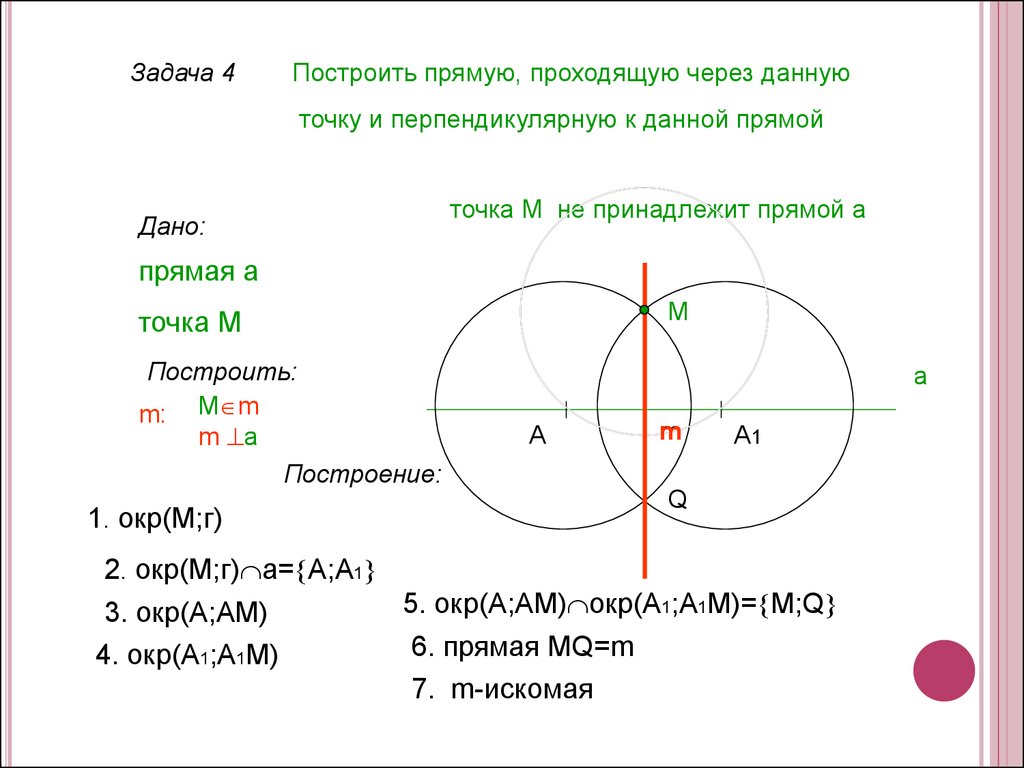
Построение:
1. окр(М;г)
а
A
m
A1
Q
2. окр(М;г) а= А;А1
5. окр(А;АМ) окр(А1;А1М)= M;Q
3. окр(А;АМ)
6. прямая МQ=m
4. окр(А1;A1М)
7. m-искомая

12.

Задача 4
Построить прямую, проходящую через данную
точку и перпендикулярную к данной прямой
Дано:
точка М не принадлежит прямой а
прямая а
точка M
Построить:
М
1 2
M m
О
m:
m a
m
A
Доказательство:
AМQ= А1MQ( по трем
Q
сторонам)
так как 1) AM=А1M=г
2) AQ=A1Q=г
3) MQ-общая
Следовательно, 1= 2.
Тогда, МО-биссектриса равнобедренного
АМА1.
Значит, МО и высота АМА1. Тогда, МQ a.
а
A1

13.

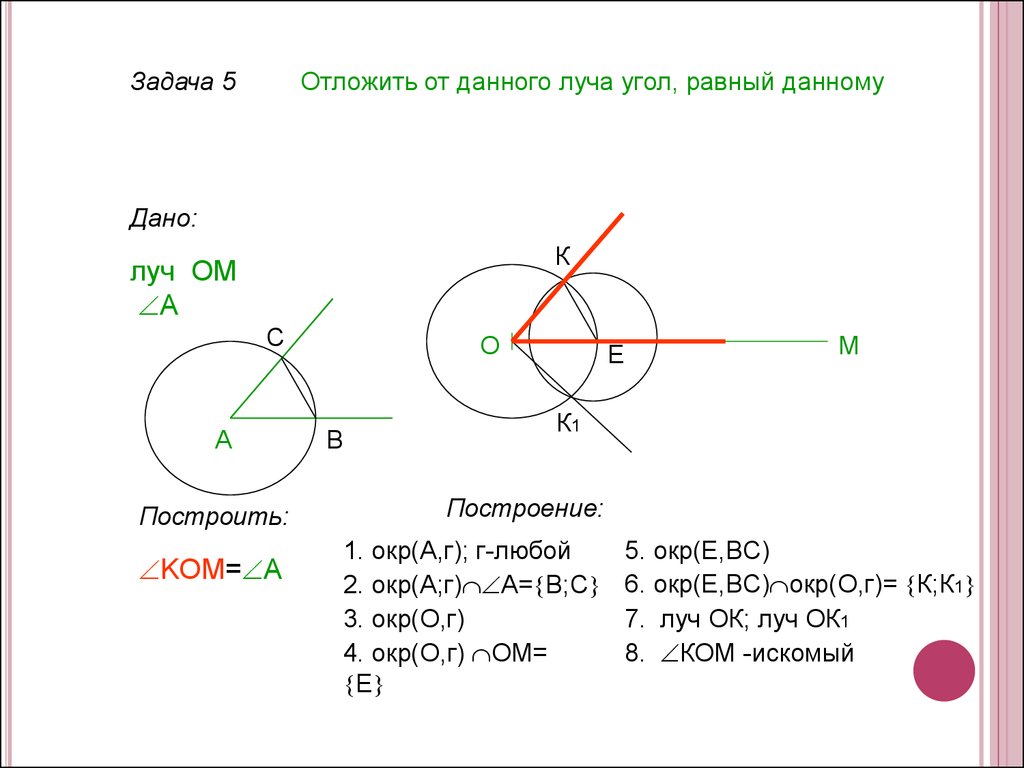
Задача 5
Отложить от данного луча угол, равный данному
Дано:
К
луч ОМ
А
С
А
Построить:
KOM= А
О
В
Е
М
К1
Построение:
1. окр(А,г); г-любой
2. окр(А;г) А= В;С
3. окр(О,г)
4. окр(О,г) ОМ=
Е
5. окр(Е,ВC)
6. окр(Е,BС) окр(О,г)= К;К1
7. луч ОК; луч ОК1
8. КОМ -искомый

14.

Задача 5
Отложить от данного луча угол, равный данному
Дано:
К
луч ОМ
А
С
А
О
В
Е
К1
Доказательство:
Построить:
KOM= А
AВС= ОЕК(по трем сторонам)
так как 1) АВ=ОЕ=г
2) АС=ОК=г
3) ВС=ЕК=г1
Следовательно, КОМ= А
М

15.

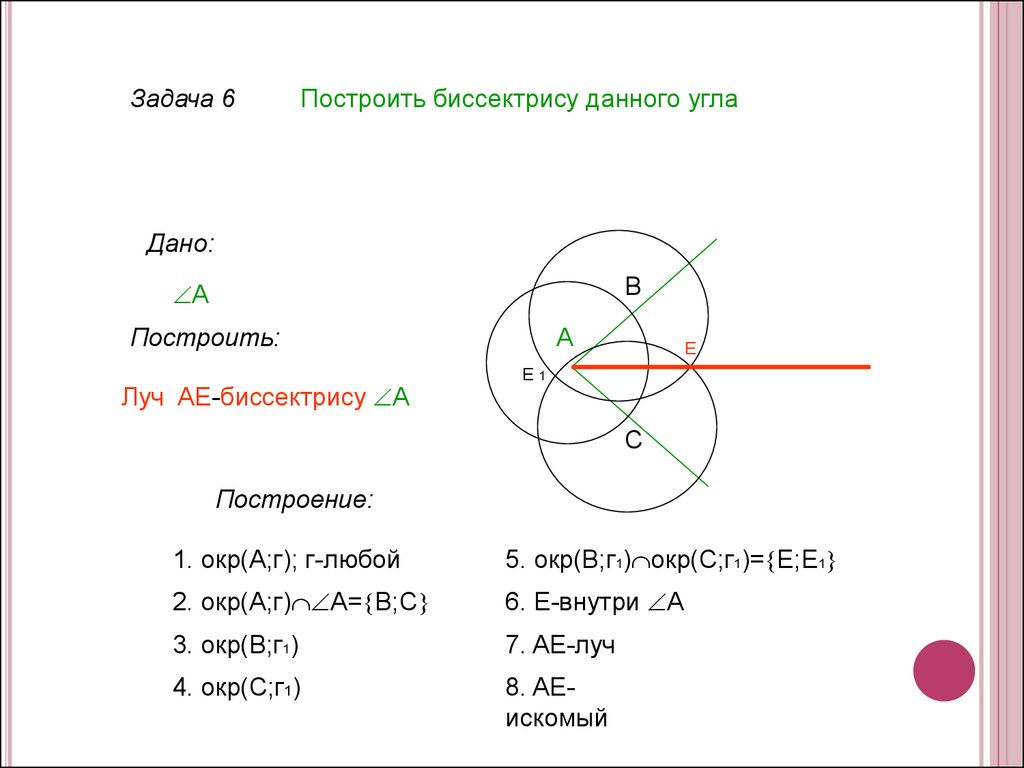
Задача 6
Построить биссектрису данного угла
Дано:
B
А
Построить:
Луч AE-биссектрису А
А
E
Е
E1
C
Построение:
1. окр(А;г); г-любой
5. окр(В;г1) окр(С;г1)= Е;E1
2. окр(А;г) А= В;С
6. Е-внутри A
3. окр(В;г1)
7. AE-луч
4. окр(С;г1)
8. AEискомый