Задачи на построение с помощью циркуля и линейки. 7 класс

1.

2.

В геометрии специально выделяют задачи на
построение, которые решаются только с помощью
двух инструментов:
ЦИРКУЛЯ И ЛИНЕЙКИ
без масштабных делений.

3.

Условные обозначения
Окр (О;r) - окружность с центром в точке О и
радиусом r
- знак угла
- знак принадлежности
- знак перпендикулярности
-
знак пересечения
- в скобках указано множество точек
пересечения
: - заменяет слова ”такой что”

4.

Задача 1
На данном луче от его начала
отложить отрезок, равный данному
Дано:
Луч h, О- начало
PQ-отрезок
P
Q
Построить:
A
O
Построение:
1. окр(О;PQ)
2. h окр(O;PQ)= A
OA:
A h
OA=PQ
3. OA-искомый
h

5.

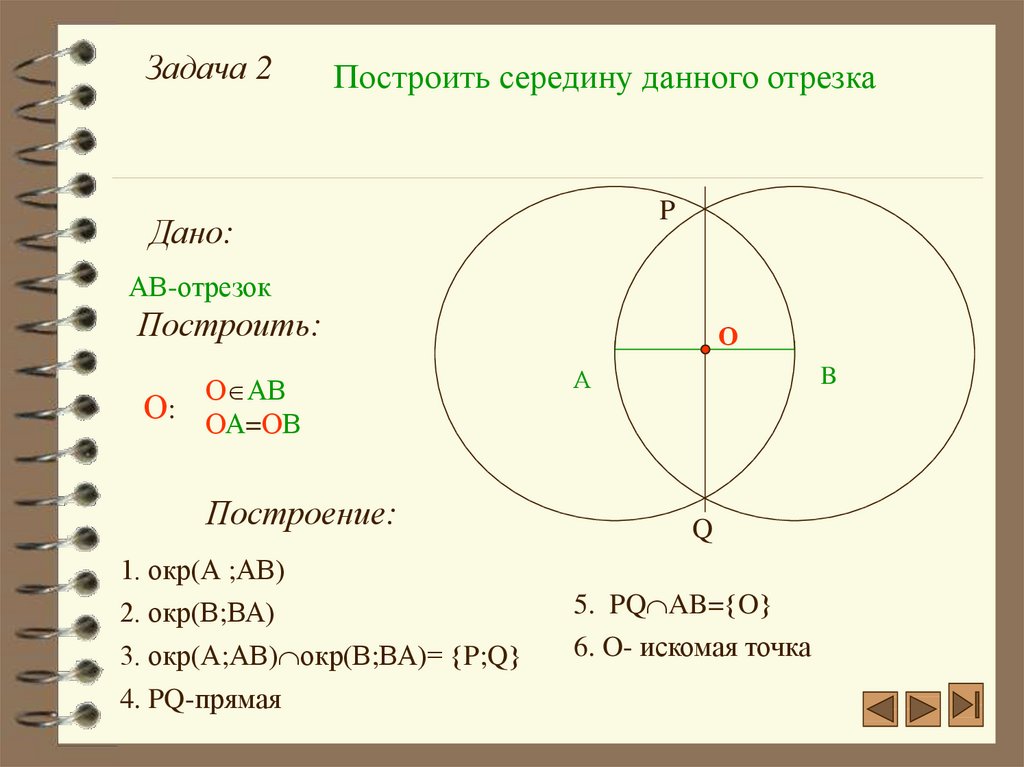
Задача 2
Построить середину данного отрезка
P
Дано:
АВ-отрезок
Построить:
О:
О АВ
ОА=ОВ
Построение:
1. окр(А ;АВ)
2. окр(В;ВА)
3. окр(А;АВ) окр(В;ВА)= P;Q
4. PQ-прямая
О
O
А
B
Q
5. PQ AB= O
6. O- искомая точка

6.

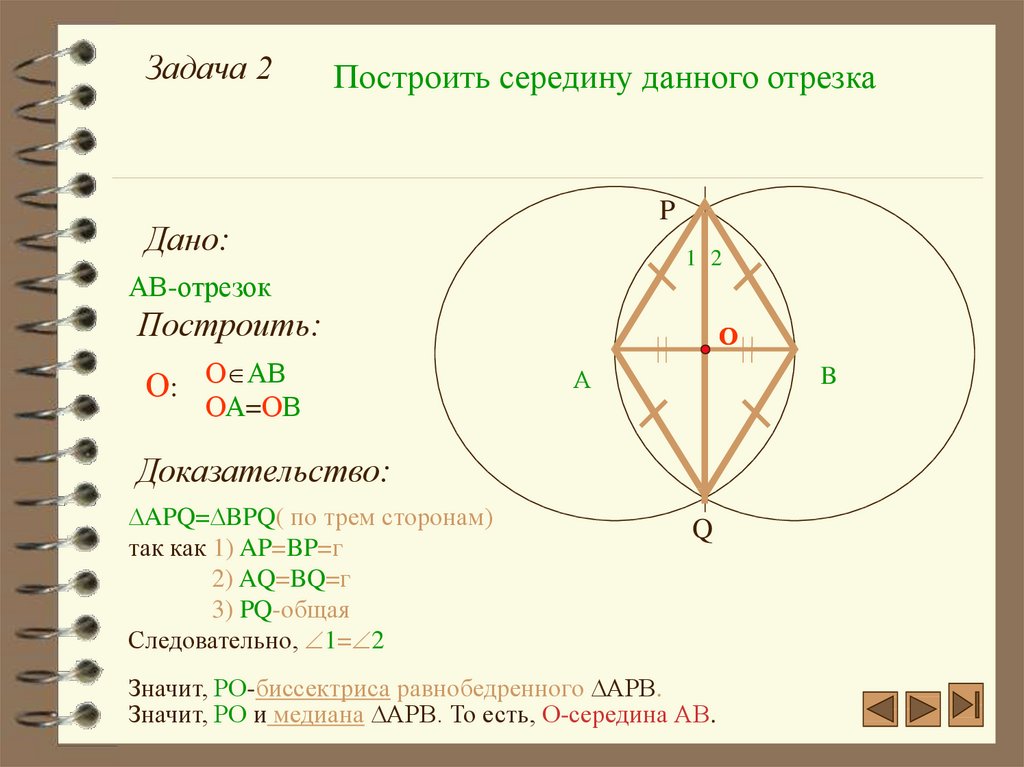
Задача 2
Построить середину данного отрезка
P
Дано:
1 2
АВ-отрезок
Построить:
О: О АВ
ОА=ОВ
О
А
B
Доказательство:
APQ= BPQ( по трем сторонам)
так как 1) AP=BP=г
2) AQ=BQ=г
3) PQ-общая
Следовательно, 1= 2
Q
Значит, РО-биссектриса равнобедренного АРВ.
Значит, РО и медиана АРВ. То есть, О-середина АВ.

7.

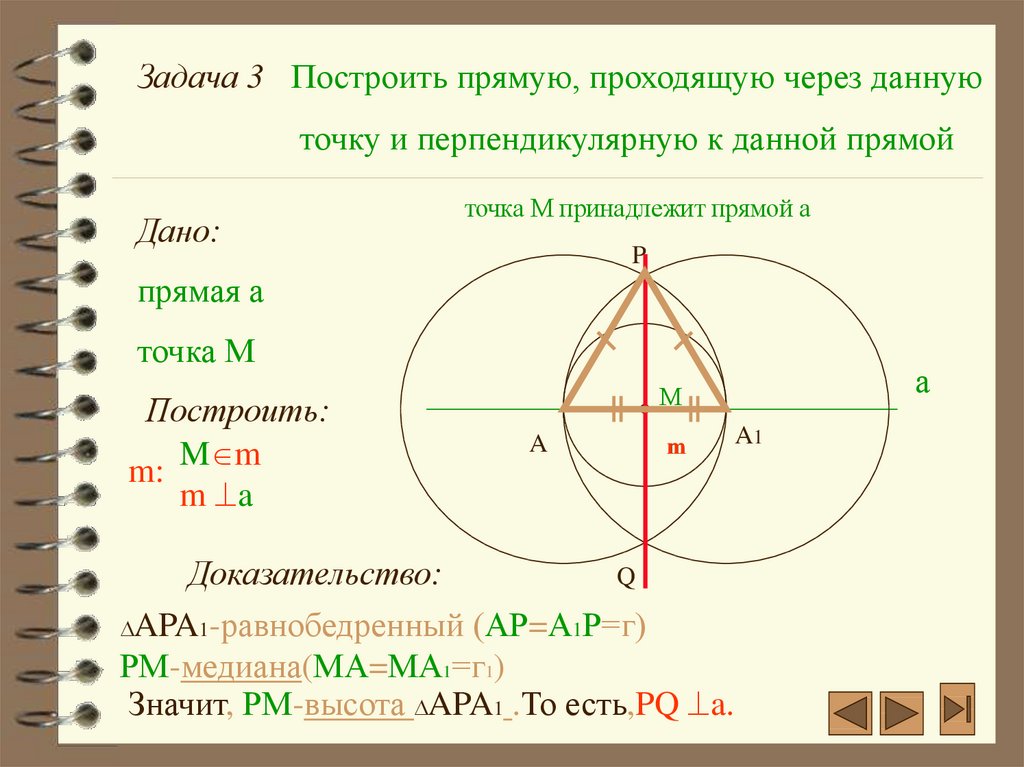
Задача 3 Построить прямую, проходящую через данную
точку и перпендикулярную к данной прямой
точка М принадлежит прямой а
Дано:
P
прямая а
точка M
Построить:
A
m: M m
m a
Построение:
1. окр(М;г); г-любой
а
М
m
Q
A1
4. окр(А1;A1A)
2. окр(М;г) а= А;А1
5. окр(А;АА1) окр(А1;А)= P;Q
3. окр(А;АА1)
6. прямая PQ=m
7. m-искомая

8.

Задача 3 Построить прямую, проходящую через данную
точку и перпендикулярную к данной прямой
Дано:
точка М принадлежит прямой а
P
прямая а
точка M
Построить:
m: M m
m a
а
М
A
m
Доказательство:
Q
APA1-равнобедренный (АР=А1Р=г)
РМ-медиана(МA=MА1=г1)
Значит, РМ-высота APA1 .То есть,PQ a.
A1

9.

Задача 4
Построить прямую, проходящую через данную
точку и перпендикулярную к данной прямой
точка М не принадлежит прямой а
Дано:
прямая а
М
точка M
а
Построить:
A
m: M m
m a
m
m
A1
Q
Построение:
1. окр(М;г)
4. окр(А1;A1М)
2. окр(М;г) а= А;А1 5. окр(А;АМ) окр(А1;А1М)= M;Q
3. окр(А;АМ)
6. прямая МQ=m
7. m-искомая

10.

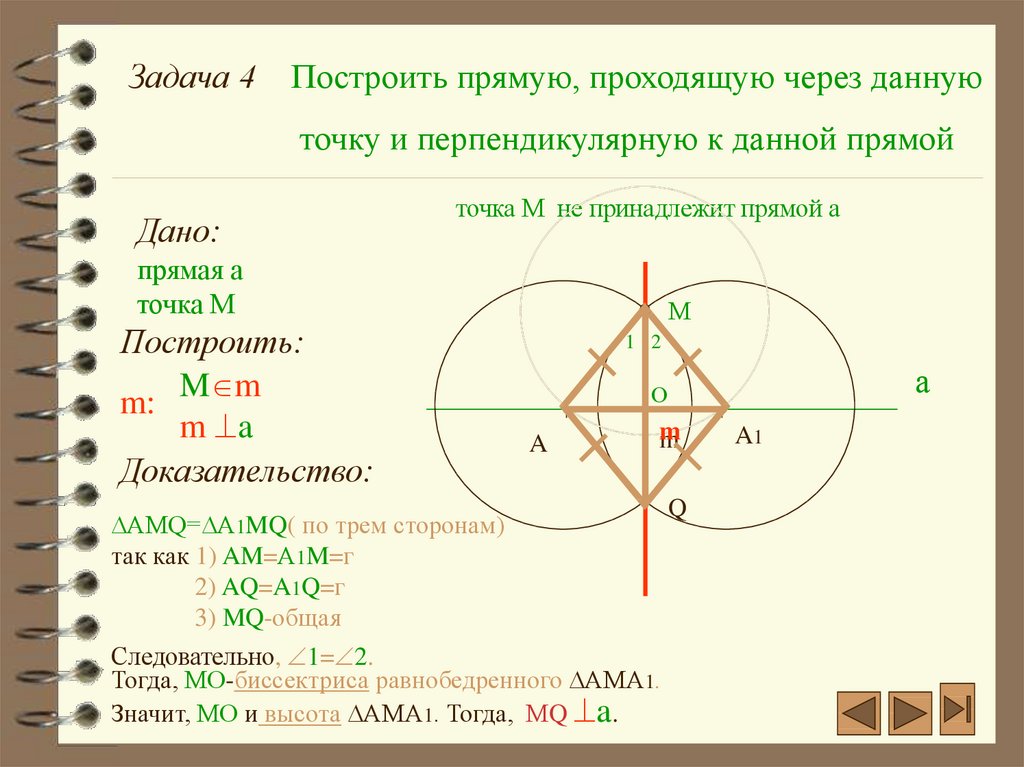
Задача 4
Построить прямую, проходящую через данную
точку и перпендикулярную к данной прямой
Дано:
точка М не принадлежит прямой а
прямая а
точка M
Построить:
m: M m
m a
Доказательство:
М
1 2
а
О
A
m
m
AМQ= А1MQ( по трем сторонам)
так как 1) AM=А1M=г
2) AQ=A1Q=г
3) MQ-общая
Следовательно, 1= 2.
Тогда, МО-биссектриса равнобедренного АМА1.
Значит, МО и высота АМА1. Тогда, МQ a.
Q
A1