Теорема синусов

1.

2.

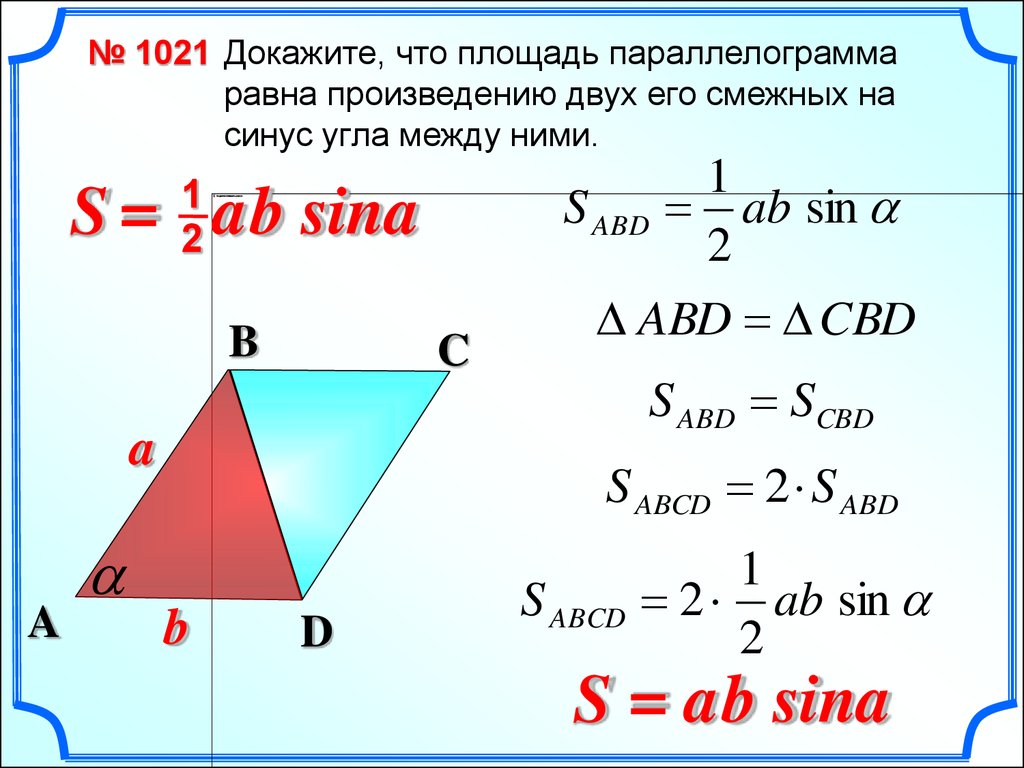
№ 1021 Докажите, что площадь параллелограмма
равна произведению двух его смежных на
синус угла между ними.
1
2
S = ab sina
B
C
a
A
S ABD
1
ab sin
2
ABD CBD
S ABD SCBD
S ABCD 2 S ABD
b
D
S ABCD
1
2 ab sin
2
S = ab sina

3.

B
C
d1
2
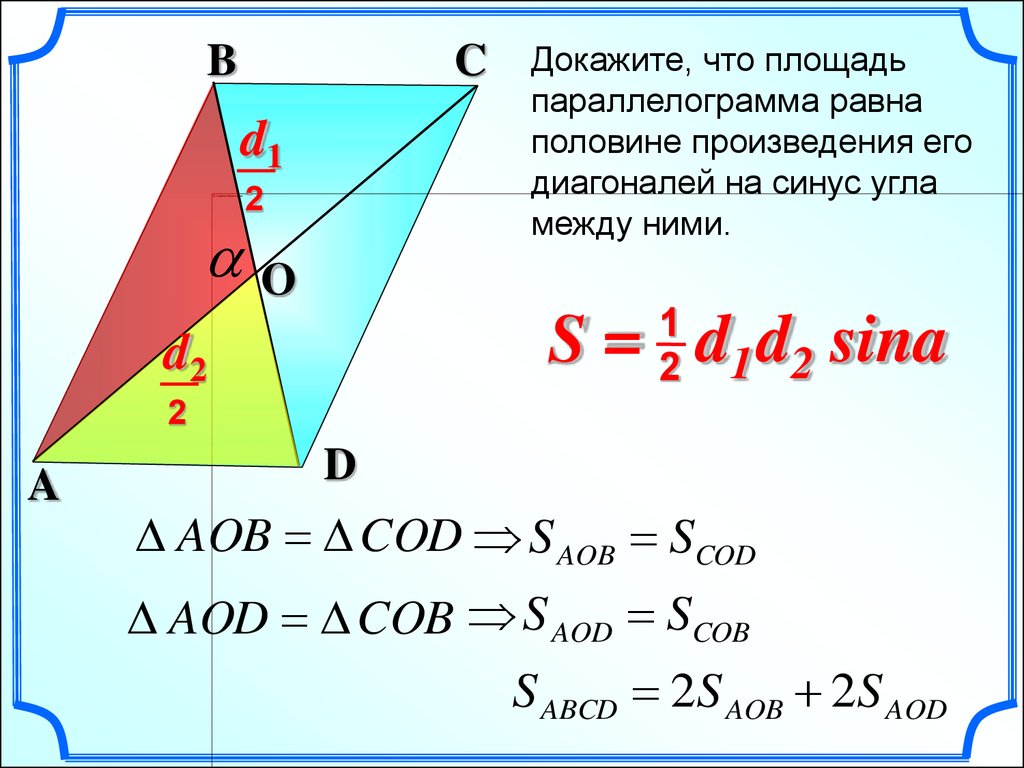
Докажите, что площадь
параллелограмма равна
половине произведения его
диагоналей на синус угла
между ними.
O
1
2
S = d1 d2 sina
d2
2
A
D
AOB COD S AOB SCOD
AOD COB S AOD SCOB
S ABCD 2S AOB 2S AOD

4.

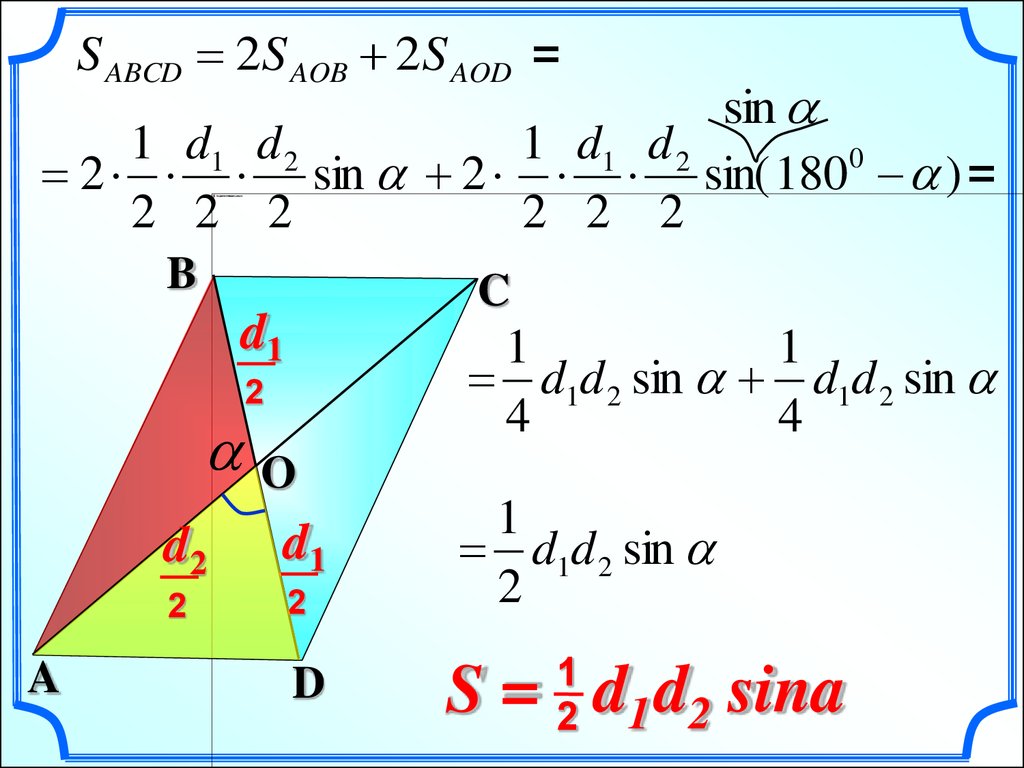
S ABCD 2S AOB 2S AOD =
sin
1 d1 d 2
1 d1 d 2
0
2 sin 2 sin( 180 ) =
2 2 2
2 2 2
B
C
d1
A
1
1
d1d 2 sin d1d 2 sin
4
4
2
O
d2
d1
2
2
D
1
d1d 2 sin
2
1
2
S = d1 d2 sina

5.

B
a
1
2
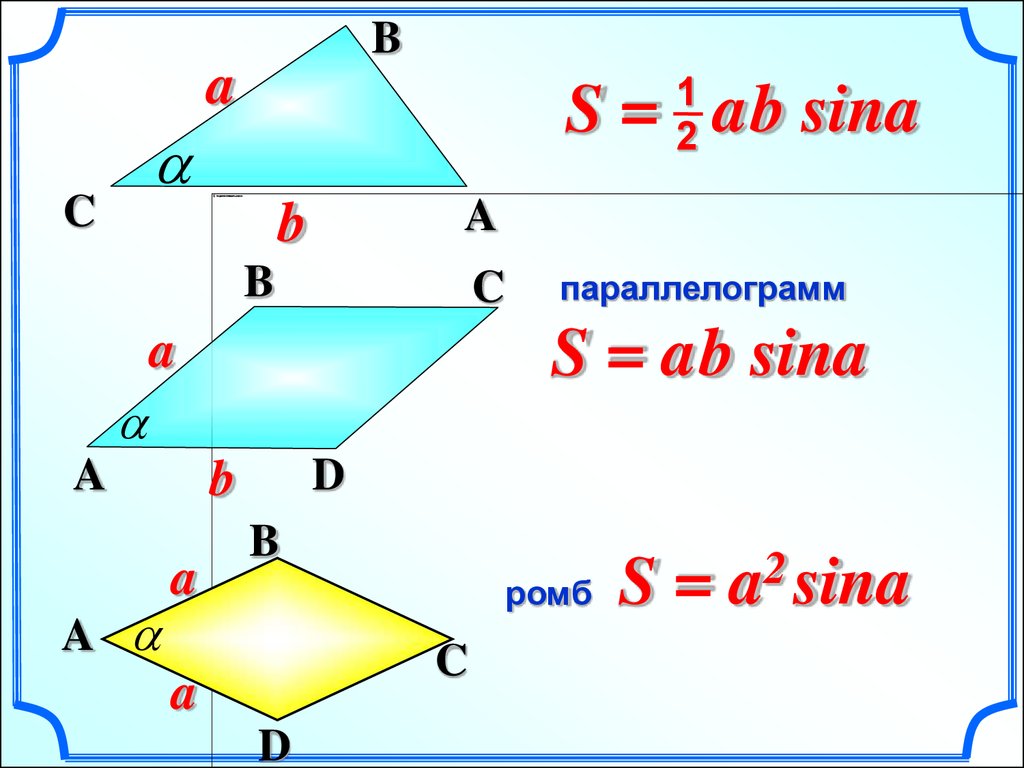
S = ab sina
C
A
b
B
C
S = ab sina
a
A
A
D
b
a
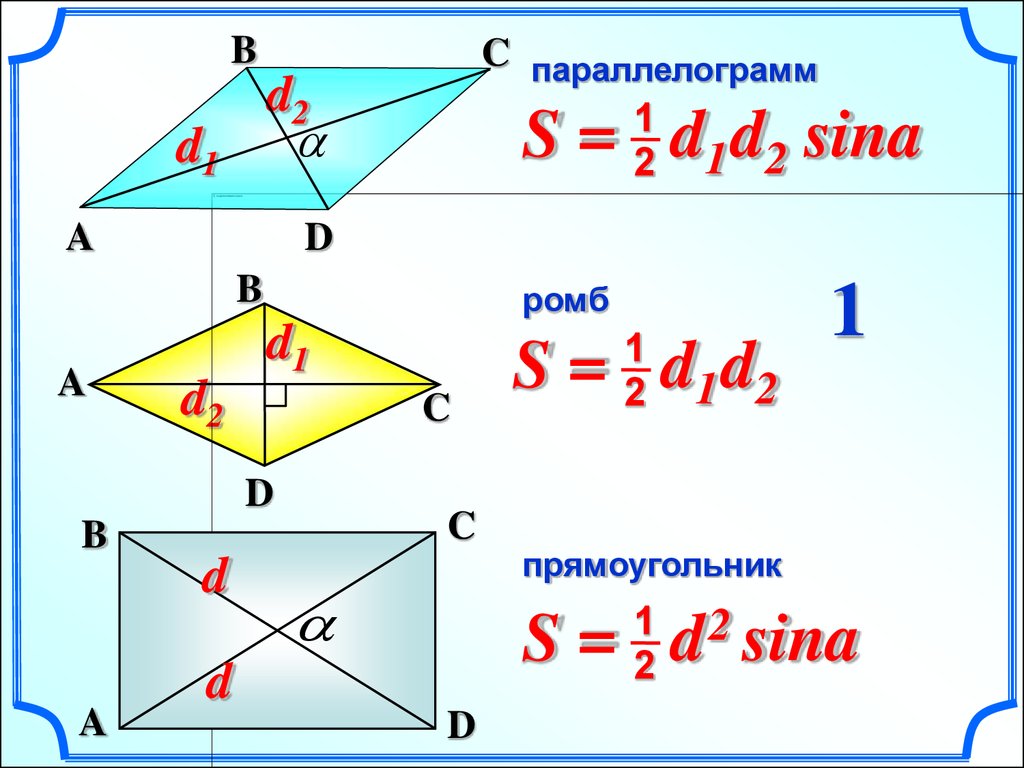
параллелограмм
B
ромб
C
a
D
S=
2
a sina

6.

B
C параллелограмм
1
2 1 2
d2
d1
A
S = d d sina
D
B
A
ромб
d1
d2
C
D
C
B
d
A
1
2
S = d1 d2 sin900
прямоугольник
S=
d
D
1
1
2
2
d sina

7.

8.

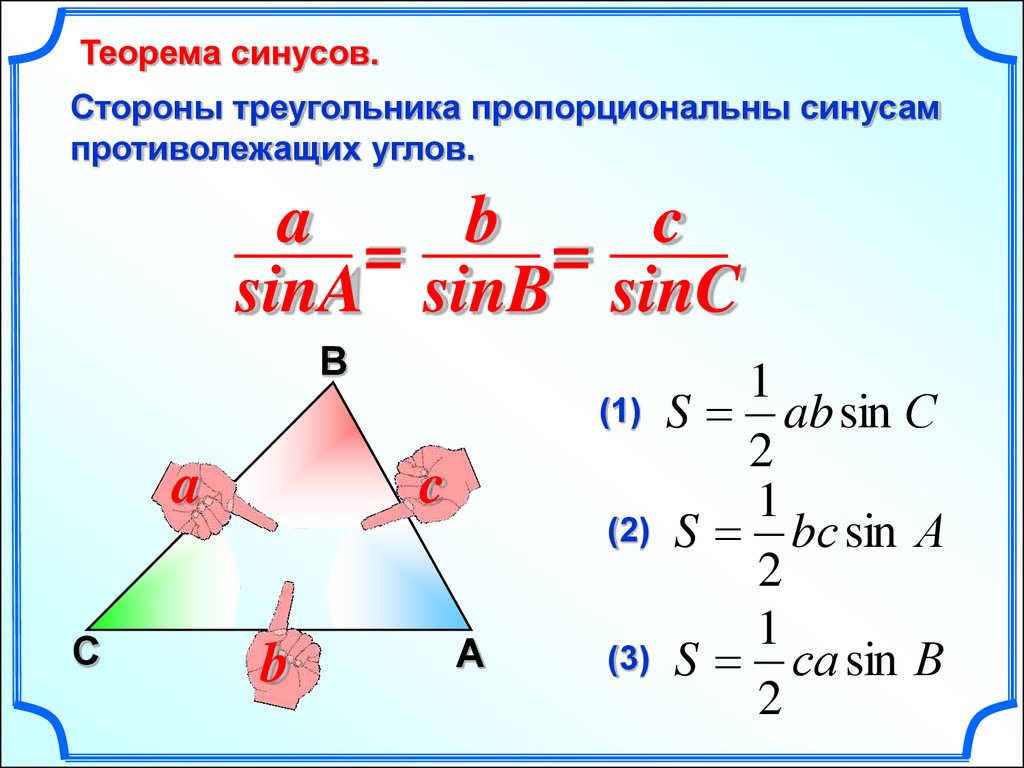
Теорема синусов.
Стороны треугольника пропорциональны синусам
противолежащих углов.
a = b = c
sinA sinB sinC
В
(1)
a
c
(2)
C
b
A
(3)
1
S ab sin С
2
1
S bс sin А
2
1
S са sin В
2

9.

(1)
1
S ab sin С ;
2
(2)
1
S bс sin А;
2
1
S са sin В
2
1
1
a sin C
c sin А
A
ab
С bc
2
2
: sin С sin А
=
sin С sin А
sin С sin А
a
c
sin А sin C
(3)

10.

Стороны треугольника пропорциональны синусам
противолежащих углов.
MO
MX
OX
=
=
sinX sinO sinC
O
М
X

11.

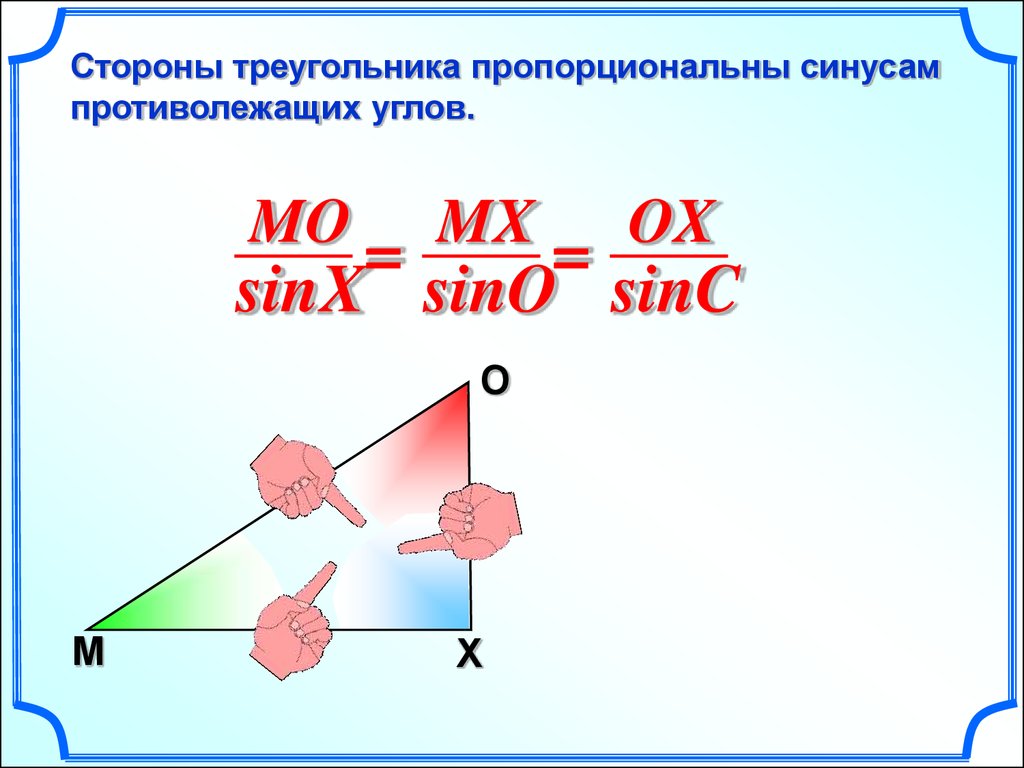
Стороны треугольника пропорциональны синусам
противолежащих углов.
CD
EC
DE
=
=
sinE sinD sinC
D
C
E

12.

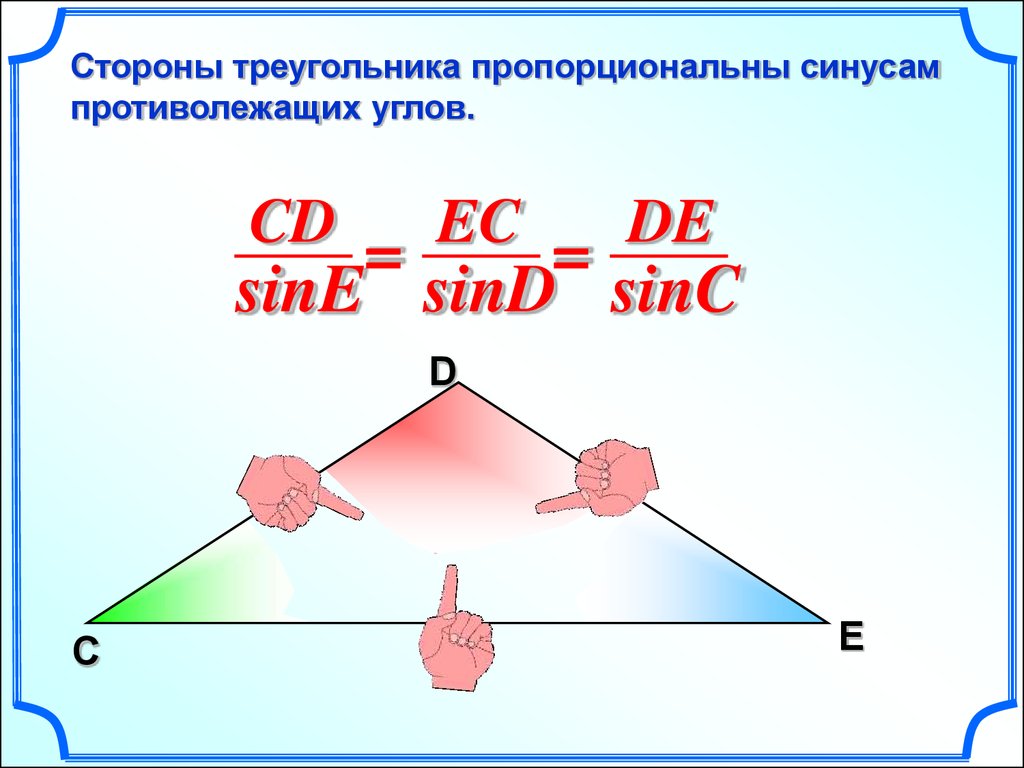
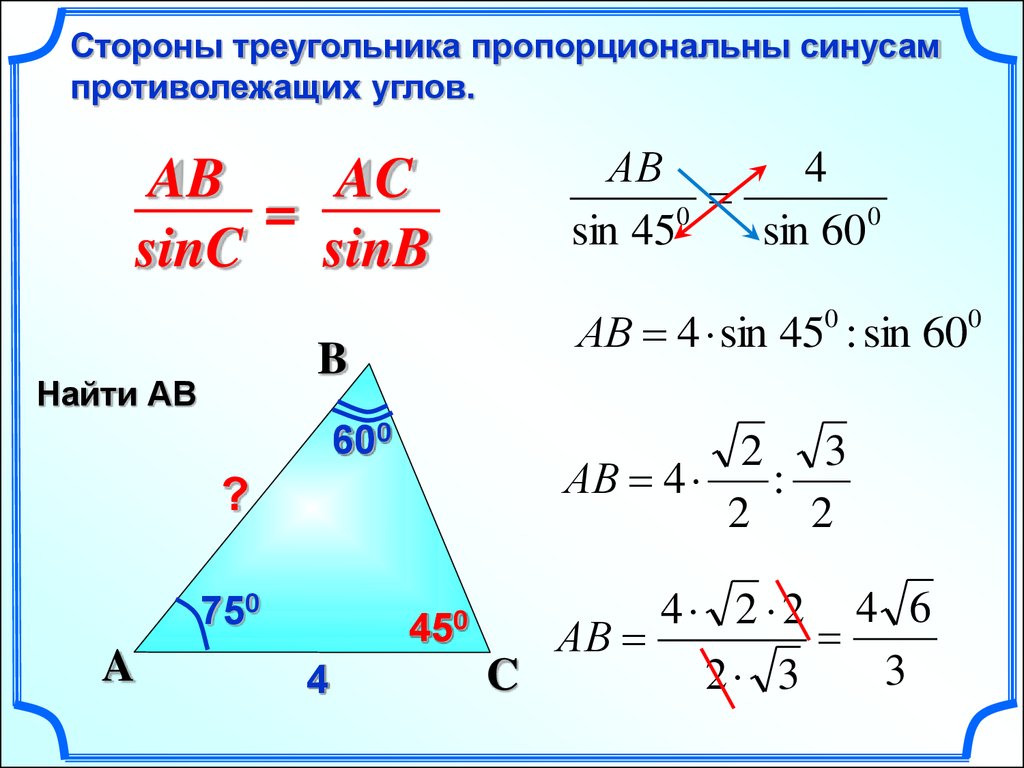
Стороны треугольника пропорциональны синусам
противолежащих углов.
AB
AC
=
sinC sinB
АВ
4
0
sin 45
sin 60 0
АВ 4 sin 45 : sin 60
0
B
Найти АВ
600
2 3
АВ 4
:
2 2
?
750
A
450
4
4 2 2 4 6
АВ
3
2 3
C
0

13.

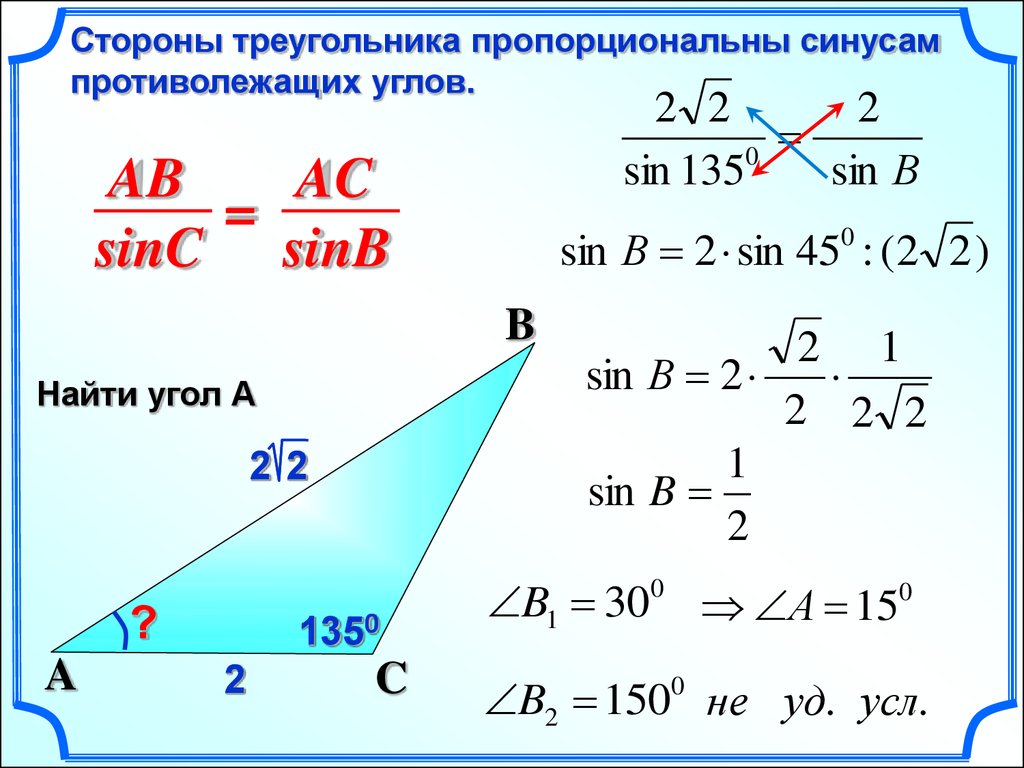
Стороны треугольника пропорциональны синусам
противолежащих углов.
2 2
2
0
sin 135
sin В
AB
AC
=
sinC sinB
sin В 2 sin 450 : (2 2 )
B
Найти угол А
22
?
A
1350
2
C
2 1
sin В 2
2 2 2
1
sin B
2
B1 30
0
А 150
B2 1500 не уд. усл.

14.

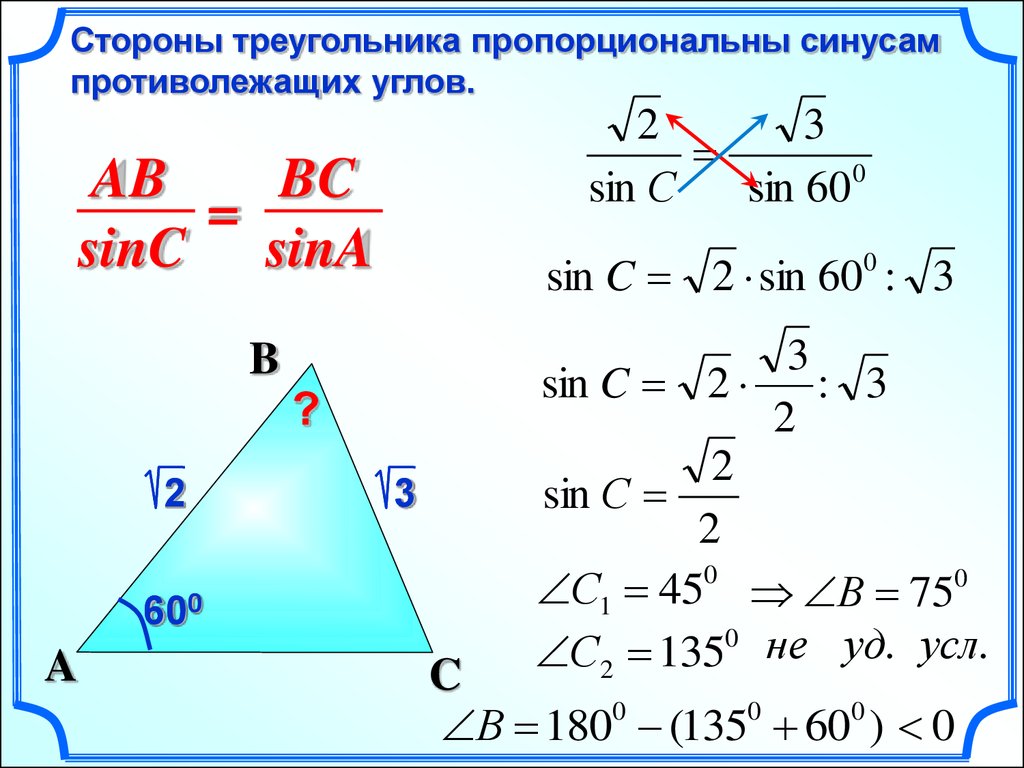
Стороны треугольника пропорциональны синусам
противолежащих углов.
2
3
0
sin С
sin 60
AB
BC
=
sinC sinA
sin C 2 sin 60 : 3
0
B
?
2
600
A
3
3
sin C 2
: 3
2
2
sin С
2
0
С1 45 В 750
0 не уд. усл.
С2 135
C
0
0
0
В 180 (135 60 ) 0

15.

ABСD – параллелограмм. Найти ВD.
Рассмотрим АВО
2
ВО
0
0
sin 45
sin 30
AB
BO
=
sinO sinA
ВО 2 sin 300 : sin 450
C
B
1350
2
450
2
O
A
2 1 2
ВО
2 2
BО 1
300
1500
1 2
ВО 2 :
2 2
D
BD 2

16.

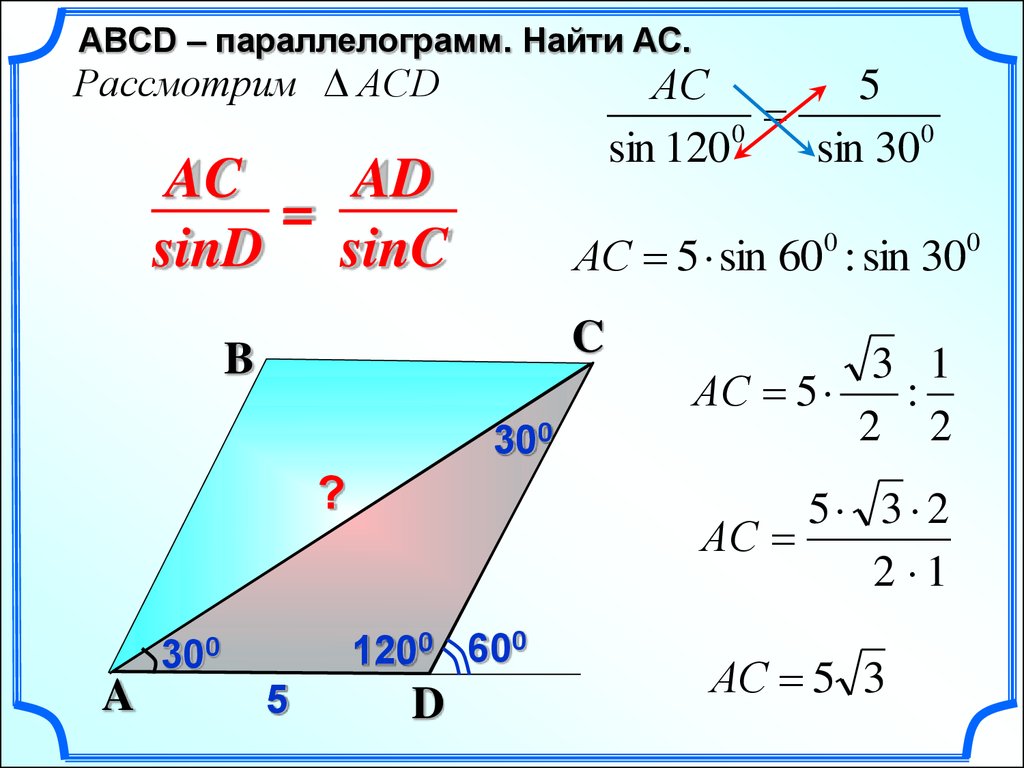
ABСD – параллелограмм. Найти AC.
Рассмотрим АCD
АС
5
0
0
sin 120
sin 30
AC
AD
=
sinD sinC
АС 5 sin 60 : sin 30
0
C
B
300
?
A
5 3 2
АС
2 1
1200 600
300
5
3 1
АС 5
:
2 2
D
АС 5 3
0

17.

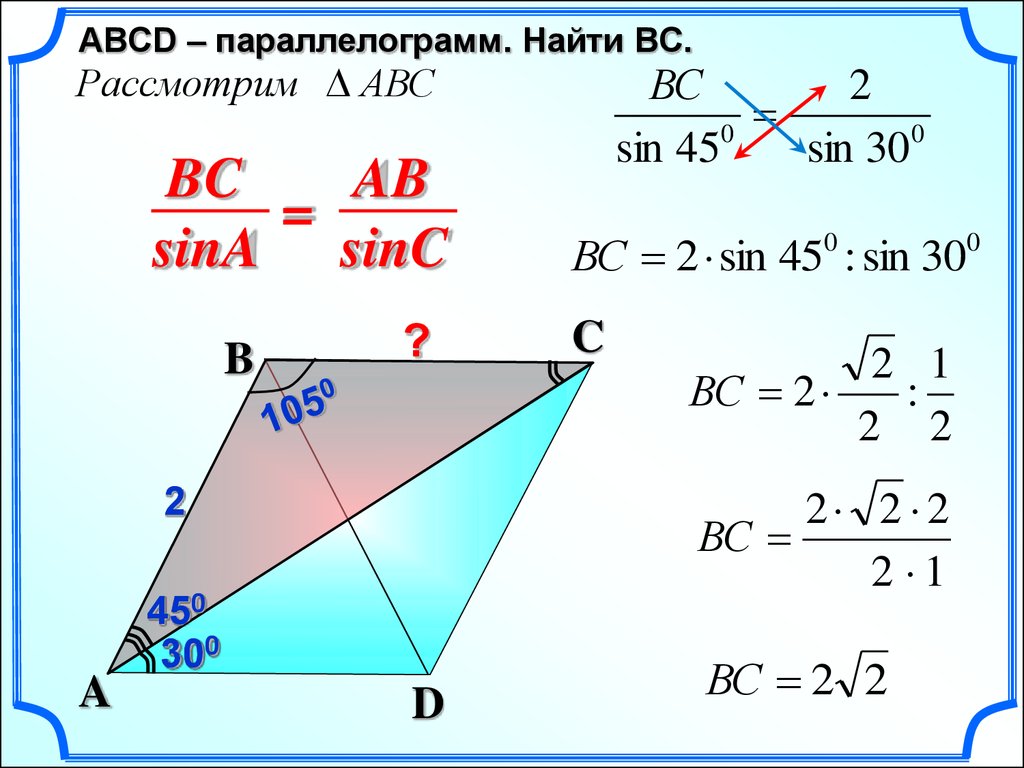
ABСD – параллелограмм. Найти BC.
Рассмотрим АВС
BC
AB
=
sinA sinC
B
?
ВС 2 sin 45 : sin 30
0
C
2 1
ВС 2
:
2 2
2 2 2
ВС
2 1
2
A
ВС
2
0
0
sin 45
sin 30
450
300
D
ВС 2 2
0

18.

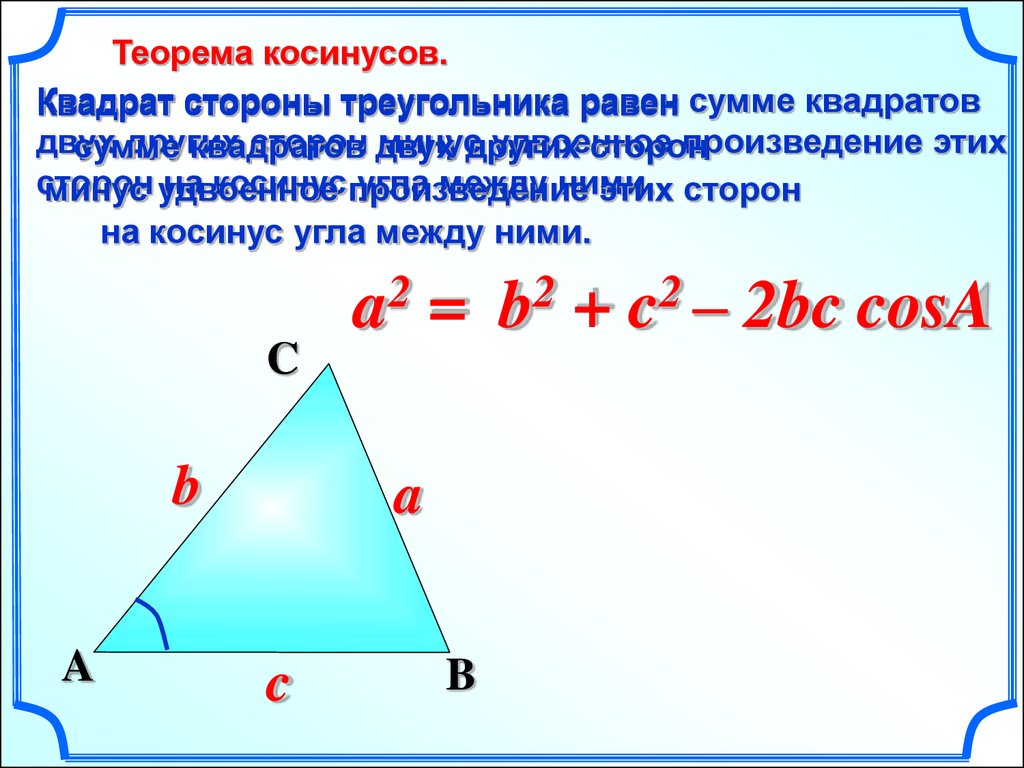
Теорема косинусов.
Квадрат стороны треугольника равен сумме квадратов
двух
других
сторон двух
минусдругих
удвоенное
произведение этих
сумме
квадратов
сторон
сторон
на косинус произведение
угла между ними.
минус удвоенное
этих сторон
на косинус угла между ними.
2
a
=
C
b
A
a
c
B
2
b
+
2
c –
2bc cosA

19.

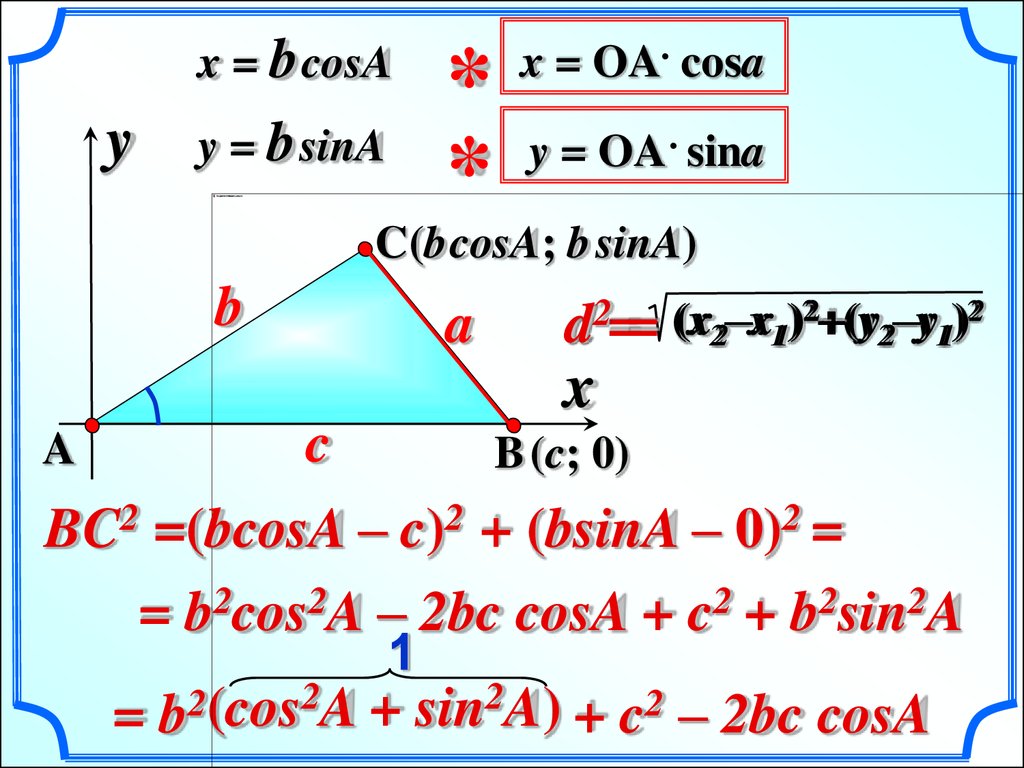
x
cos А
b
y
y
sin A
y = b sinA
b
C(bcosA; b sinA)
b
a
y
d2==
(x22–x11)22+(y22–y11)22
x
x
A
x = b cosA
B (c; 0)
c
BC2 =(bcosA – c)2 + (bsinA – 0)2 =
= b2cos2A – 2bc cosA + c2 + b2sin2A
1
=
2A +
2
(cos
b
sin2A) + c2 – 2bc cosA

20.

x = b cosA
y
*
*
y = b sinA
x = OA cosa
y = OA sina
C(bcosA; b sinA)
b
a
d2==
(x22–x11)22+(y22–y11)22
x
c
A
B (c; 0)
BC2 =(bcosA – c)2 + (bsinA – 0)2 =
= b2cos2A – 2bc cosA + c2 + b2sin2A
1
=
2A +
2
(cos
b
sin2A) + c2 – 2bc cosA

21.

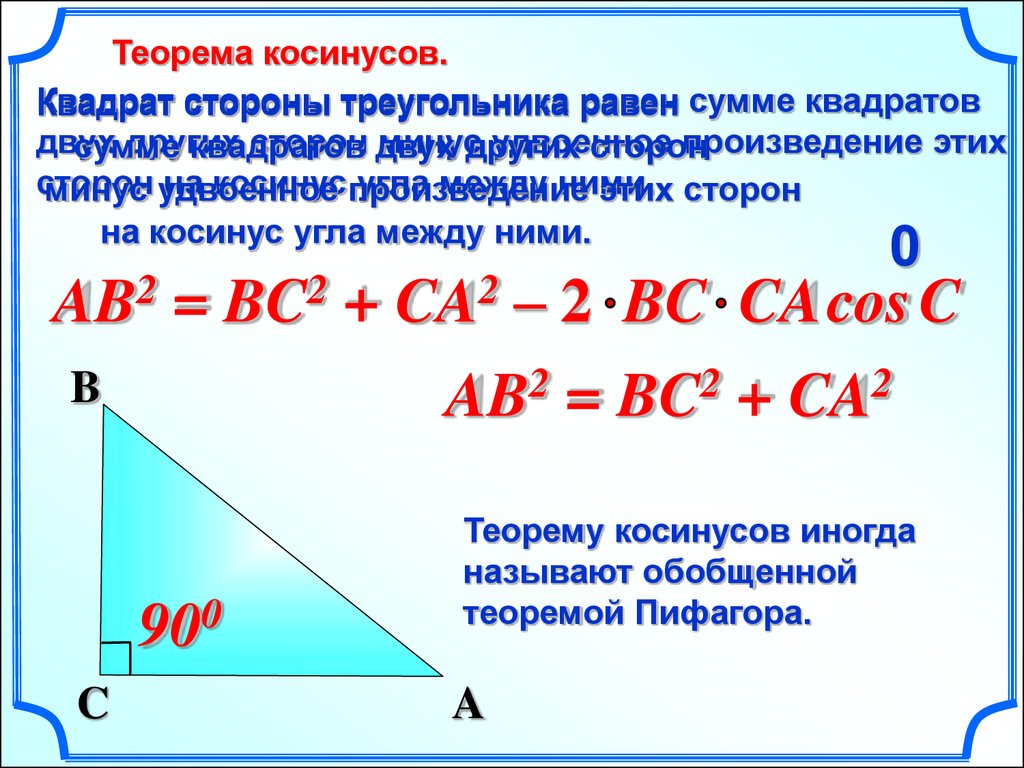
Теорема косинусов.
Квадрат стороны треугольника равен сумме квадратов
двух
других
сторон двух
минусдругих
удвоенное
произведение этих
сумме
квадратов
сторон
сторон
на косинус произведение
угла между ними.
минус удвоенное
этих сторон
на косинус угла между ними.
0
AB2 = BC2 + CA2 – 2 BC CA cos C
2
2
2
B
AB = BC + CA
900
C
Теорему косинусов иногда
называют обобщенной
теоремой Пифагора.
A

22.

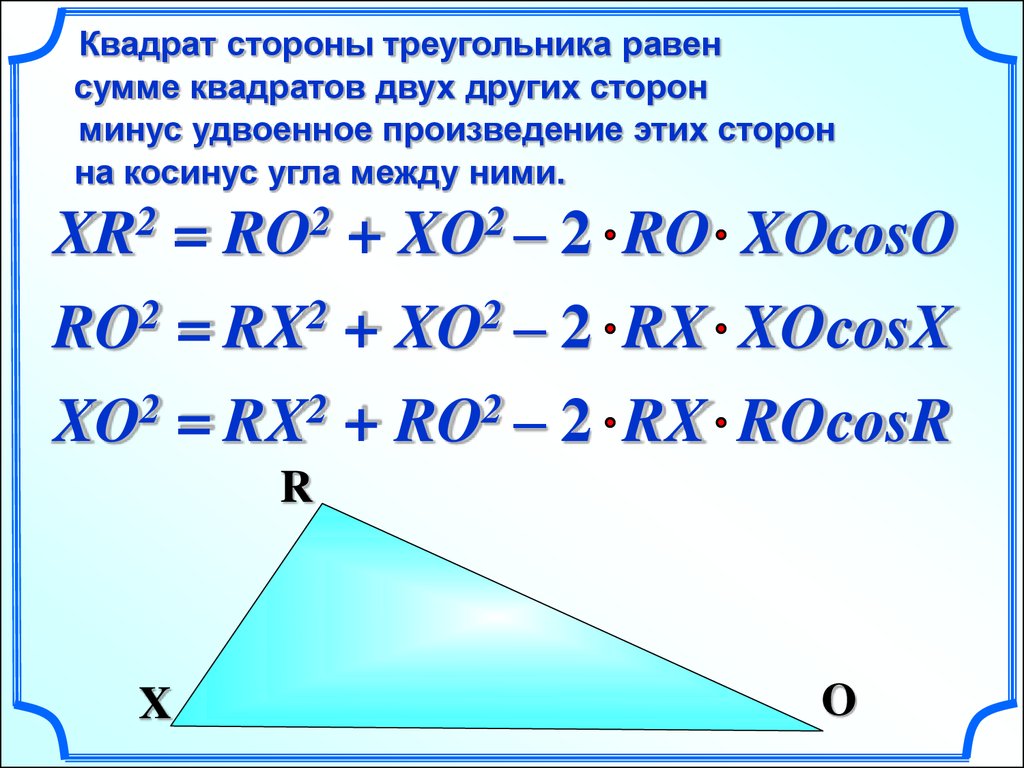
Квадрат стороны треугольника равен
сумме квадратов двух других сторон
минус удвоенное произведение этих сторон
на косинус угла между ними.
XR2 = RO2 + XO2 – 2 RO XOcosO
2
2
2
RO = RX + XO – 2 RX XOcosX
XO2 = RX2 + RO2 – 2 RX ROcosR
R
X
O

23.

F
Запишите для данного
треугольника теорему синусов
и теорему косинусов для
каждой стороны.
С
D
DF
FC
DC
sin C sin D sin F
DF 2 DC 2 CF 2 2 DC CF cos C
DС DF CF 2 DF CF cos F
2
2
2
СF DC DF 2 DC DF cos D
2
2
2

24.

с b a 2ab cos С
2
2
2
2ab cos С b a c : 2ab
2
2
2
b a c
cos С
2ab 0
2
2
2
На практике удобно сравнивать квадрат большей
стороны и сумму квадратов двух других.
b a
cc 0 cos C 0, C 90
2
2
22
0
b a
cc 0 cos C 0 , C острый
2
2
22
b a
c 0 cos C 0 , C тупой
2
2
22

25.

Определите вид треугольника со сторонами 5, 6 и 7 см.
5 6
2
2
>7
2
треугольник остроугольный
Определите вид треугольника со сторонами 2, 3 и 4 см.
2
>
2 3
2
4 треугольник тупоугольный
2
Какой угол в данном треугольнике тупой ?

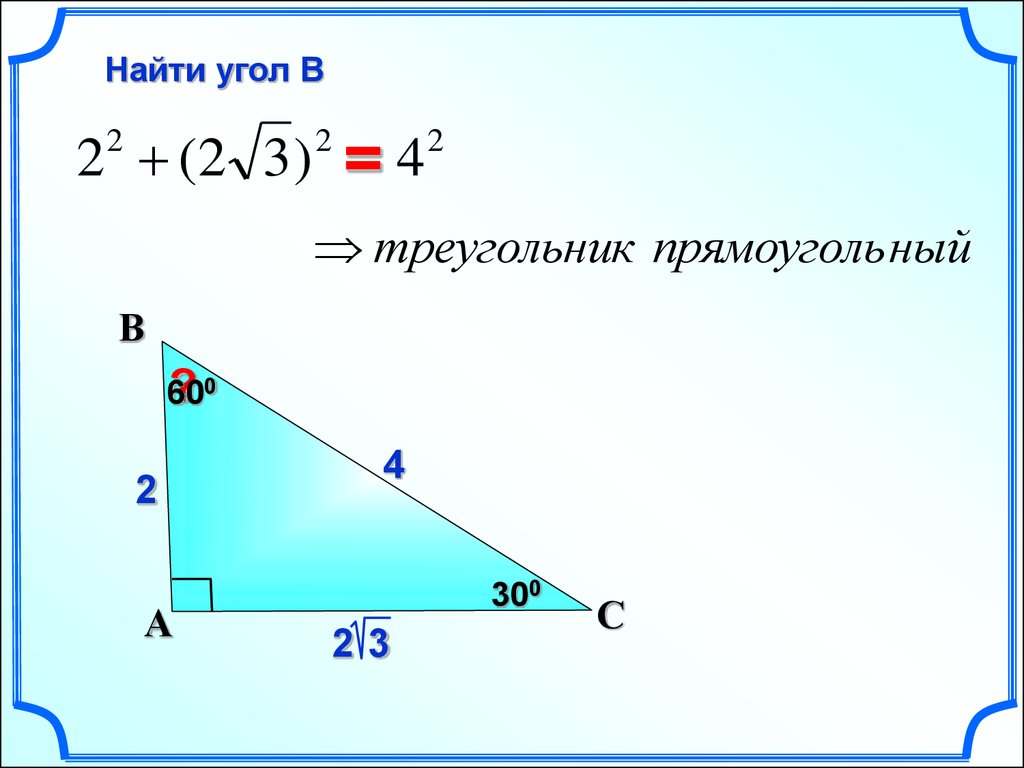
26.

Найти угол В
2 (2 3 )
2
2
=4
2
треугольник прямоуголь ный
В
?0
60
2
А
4
300
23
С

27.

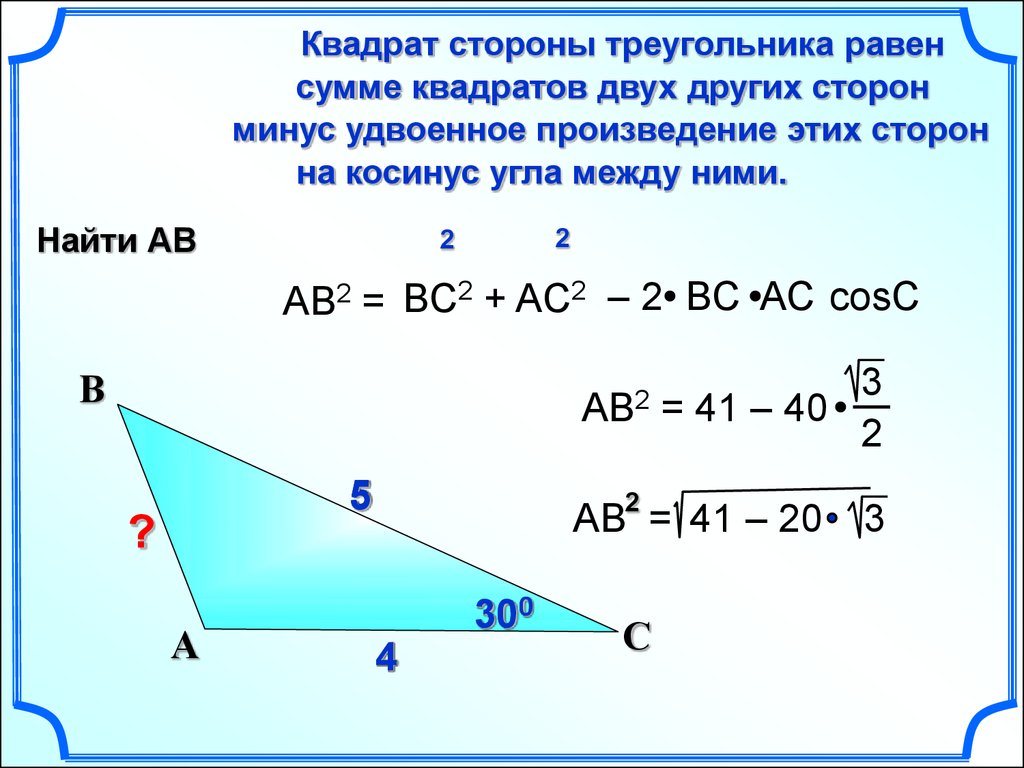
Квадрат стороны треугольника равен
сумме квадратов двух других сторон
минус удвоенное произведение этих сторон
на косинус угла между ними.
Найти АВ
2
2
AB2 = BC2 + AC2 – 2 BC AC cosC
В
AB2
5
?
А
2
3
= 41 – 40
2
AB = 41 – 20
300
4
С
3

28.

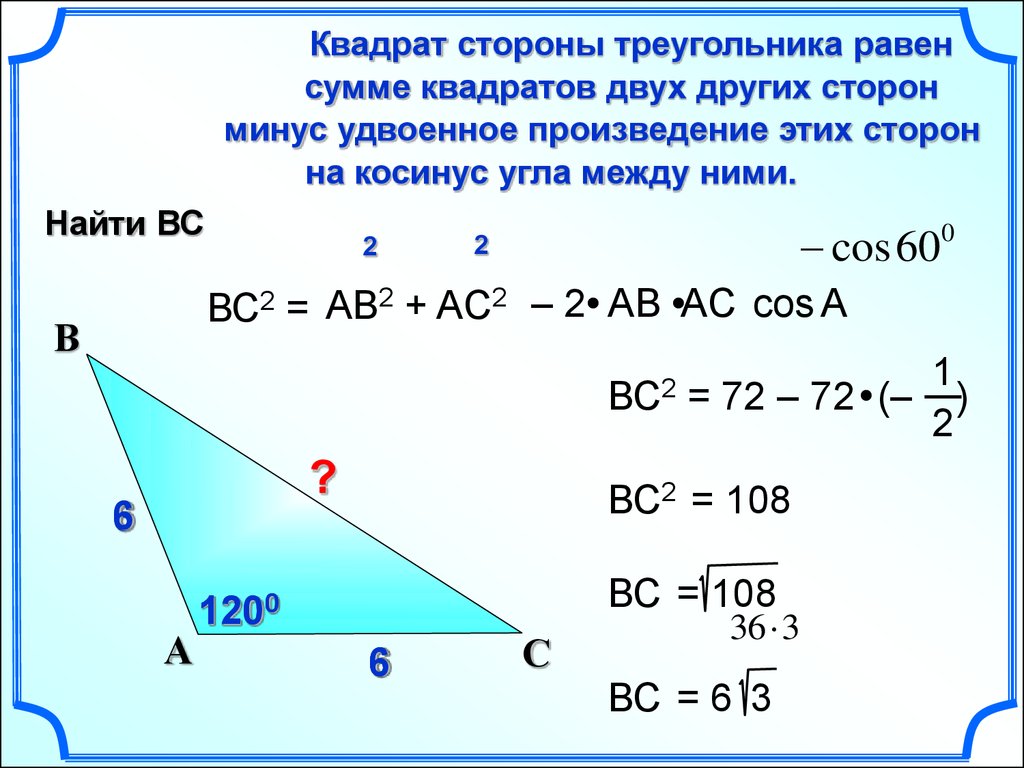
Квадрат стороны треугольника равен
сумме квадратов двух других сторон
минус удвоенное произведение этих сторон
на косинус угла между ними.
Найти ВС
2
cos 600
2
ВС2 = АВ2 + AC2 – 2 АВ AC cos А
В
ВС2
?
6
А
1
= 72 – 72 (– )
2
ВС2 = 108
ВС = 108
1200
6
С
36 3
ВС = 6 3

29.

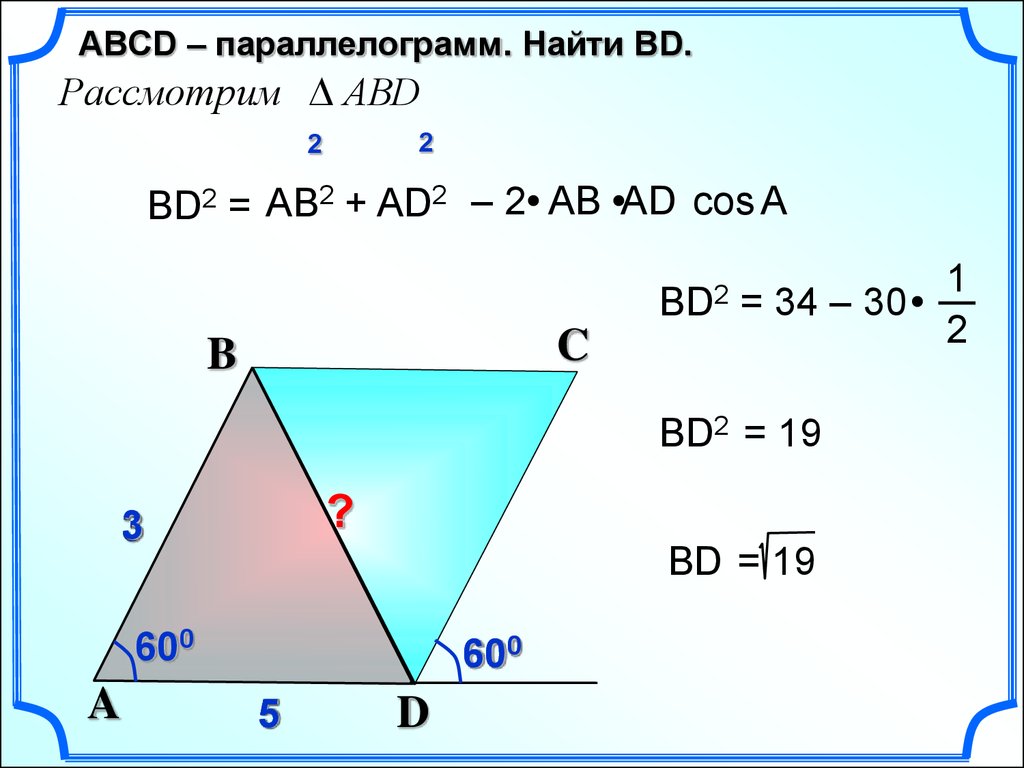
ABСD – параллелограмм. Найти ВD.
Рассмотрим АВD
2
2
ВD2 = АВ2 + AD2 – 2 АВ AD cos А
ВD2
C
B
1
= 34 – 30
2
ВD2 = 19
?
3
ВD = 19
600
A
600
5
D

30.

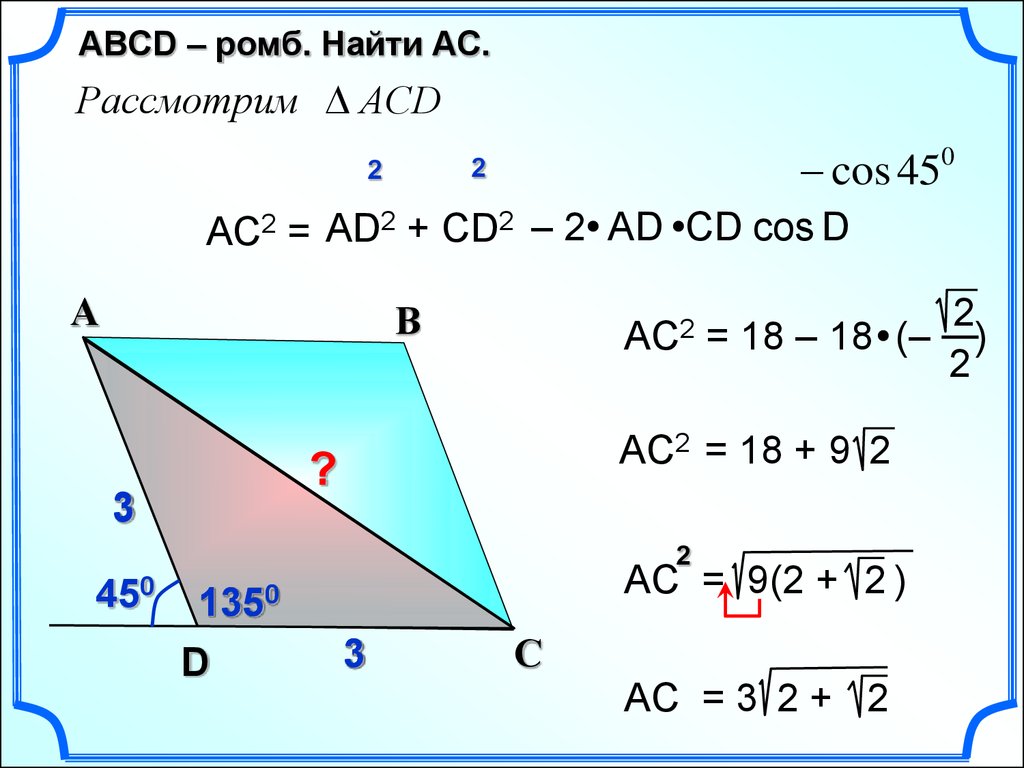
ABСD – ромб. Найти AC.
Рассмотрим АСD
cos 45
2
2
0
AC2 = АD2 + CD2 – 2 АD CD cos D
А
В
AС2
AС2 = 18 + 9 2
?
3
2
= 18 – 18 (– )
2
2
450
AC = 9(2 + 2 )
1350
D
3
С
AC = 3 2 + 2