Течение и вязкость жидкостей

1.

Лекция №2
Течение и вязкость жидкостей
1. Течение жидкости, идеальная жидкость. Уравнение
неразрывности. Уравнение Бернулли.
2. Движение вязкой жидкости. Уравнение Ньютона.
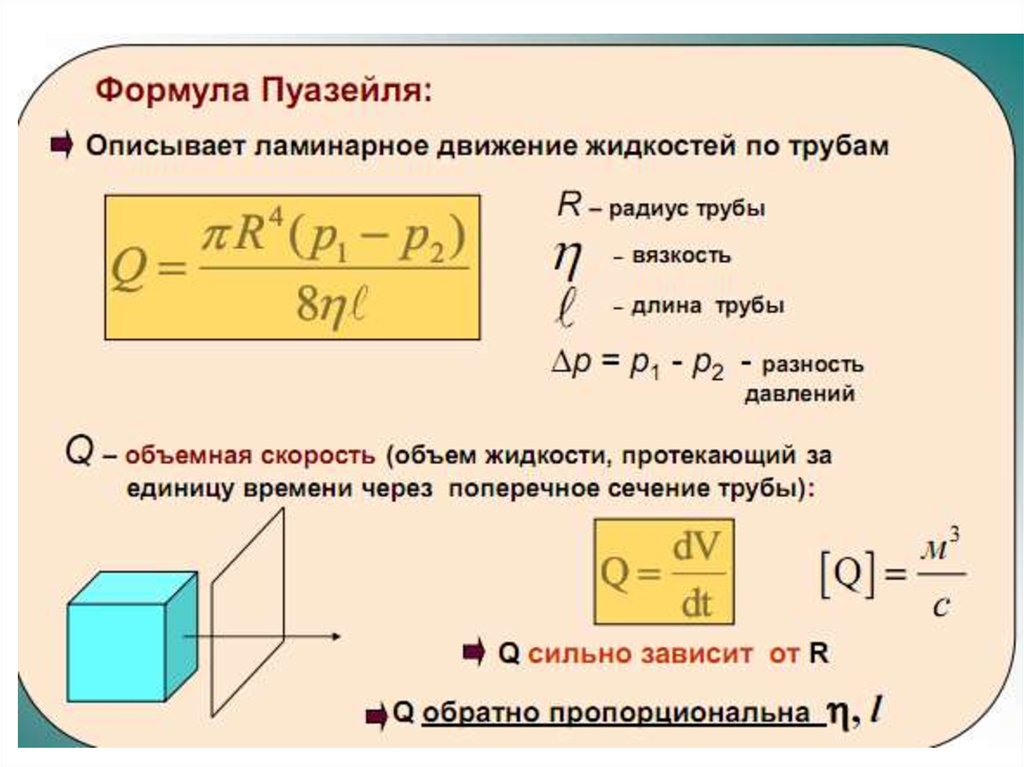
Формула Пуазейля.
3. Модель кровообращения Франка. Пульсовая волна.
Формула Моенса-Кортевега.

2.

1 вопрос - Течение жидкости, идеальная жидкость.
Уравнение неразрывности. Уравнение Бернулли.
Движение жидкостей называется течением.
Совокупность частиц движущейся жидкости называется потоком.
Графически движение жидкостей изображается с помощью
линий тока.
Часть жидкости, ограниченная линиями тока, называется
трубкой тока.

3.

Течение жидкости называется стационарным, если форма
и расположение линий тока, а также значение скоростей в
каждой ее точке со временем не изменяются.
Жидкость, в которой отсутствуют силы внутреннего
трения, называется идеальной жидкостью.
Жидкие среды составляют свыше 90% организма человека

4.

S1 1 S2 2
или
S const
- это уравнение неразрывности для несжимаемой жидкости.
Произведение скорости течения несжимаемой жидкости на
поперечное сечение трубки тока есть величина постоянная
для данной трубки тока.

5.

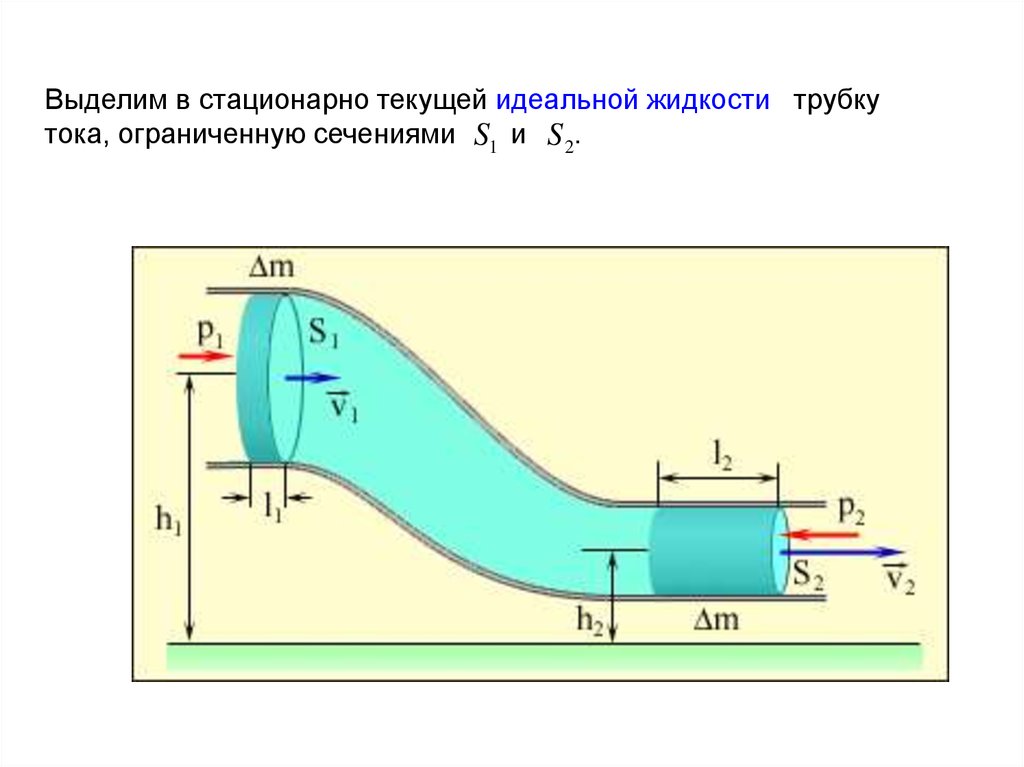
Выделим в стационарно текущей идеальной жидкости трубку
тока, ограниченную сечениями S1 и S 2.

6.

Согласно закону сохранения энергии, изменение полной
энергии идеальной несжимаемой жидкости должно быть
равно работе А внешних сил по перемещению массы m
жидкости:
E2 E1 A,
где
E1 -полная энергия жидкости массой m в местах сечения S1
E2 - то же для S 2
А – работа, совершаемая при перемещении всей жидкости,
заключенной между сечениями S1 и S 2 за малый промежуток
времени t.
A F1l1 F2l2
F1 p1S1; F2 p2 S2 ;
l1 1 t;
m 12
E1
mgh1
2
2
m 2
E2
mgh2
2
l2 2 t

7.

P1 и P2 - давления на сечениях S1 и S2.
Объединив записанные формулы , получим:
Поделив обе части на V и учитывая, что
,

8.

После ряда преобразований, используя уравнение неразрывности
получаем
2
2
1
2
или
2
2
gh1 p1
2
2
gh p const
gh2 p2
–уравнение Бернулли
В идеальной несжимаемой жидкости сумма статического, динамического и
гидростатического давлений постоянна на любом поперечном сечении потока
2
2
gh
р
- динамическое давление,
- гидростатическое давление,
- статическое давление.

9.

2 вопрос - Движение вязкой жидкости. Уравнение Ньютона.
Формула Пуазейля.
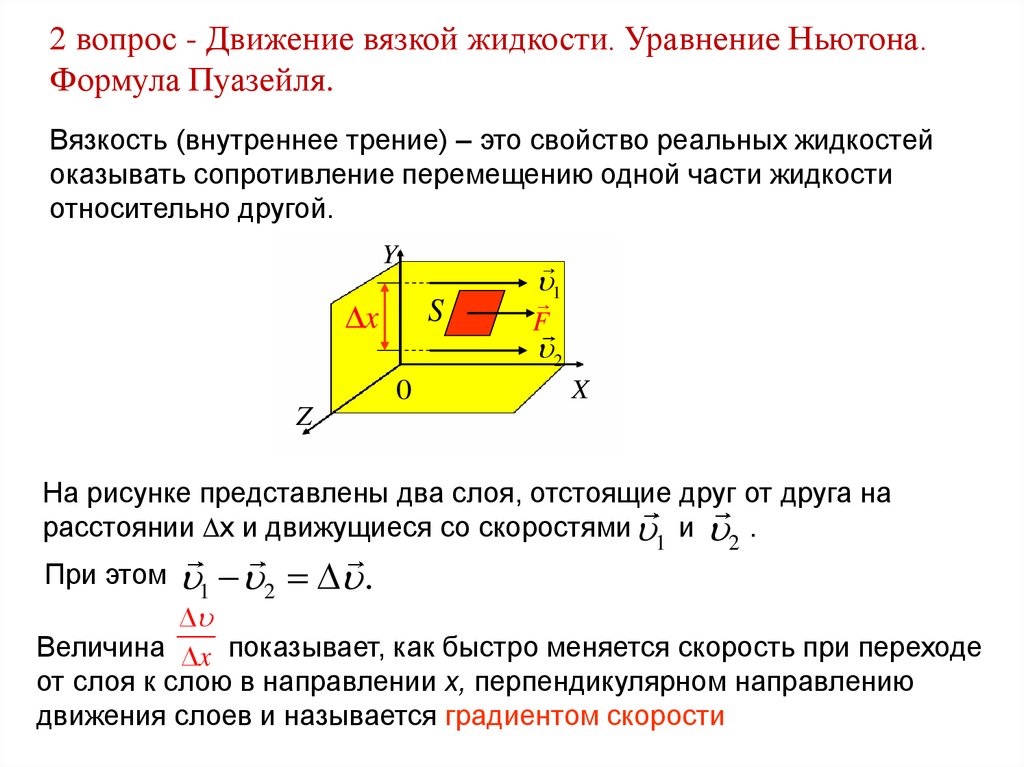
Вязкость (внутреннее трение) – это свойство реальных жидкостей
оказывать сопротивление перемещению одной части жидкости
относительно другой.
Y
x
S
0
1
F
2
X
Z
На рисунке представлены два слоя, отстоящие друг от друга на
расстоянии x и движущиеся со скоростями 1 и 2 .
При этом
1 2 .
Величина x показывает, как быстро меняется скорость при переходе
от слоя к слою в направлении x, перпендикулярном направлению
движения слоев и называется градиентом скорости

10.

11.

12.

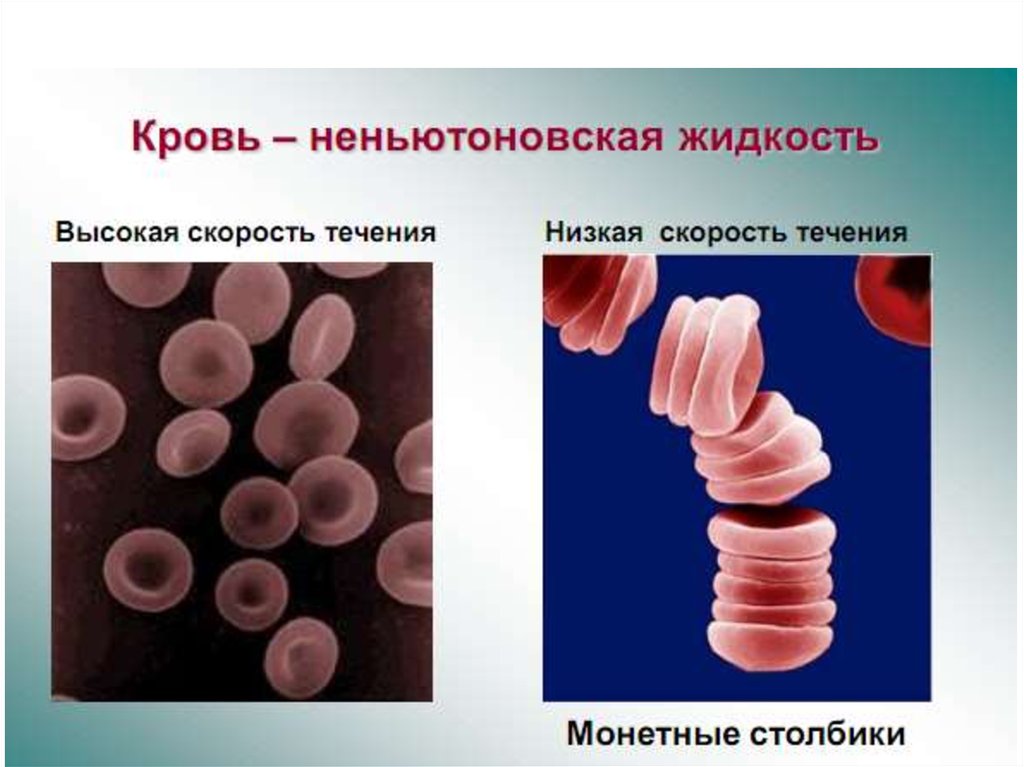
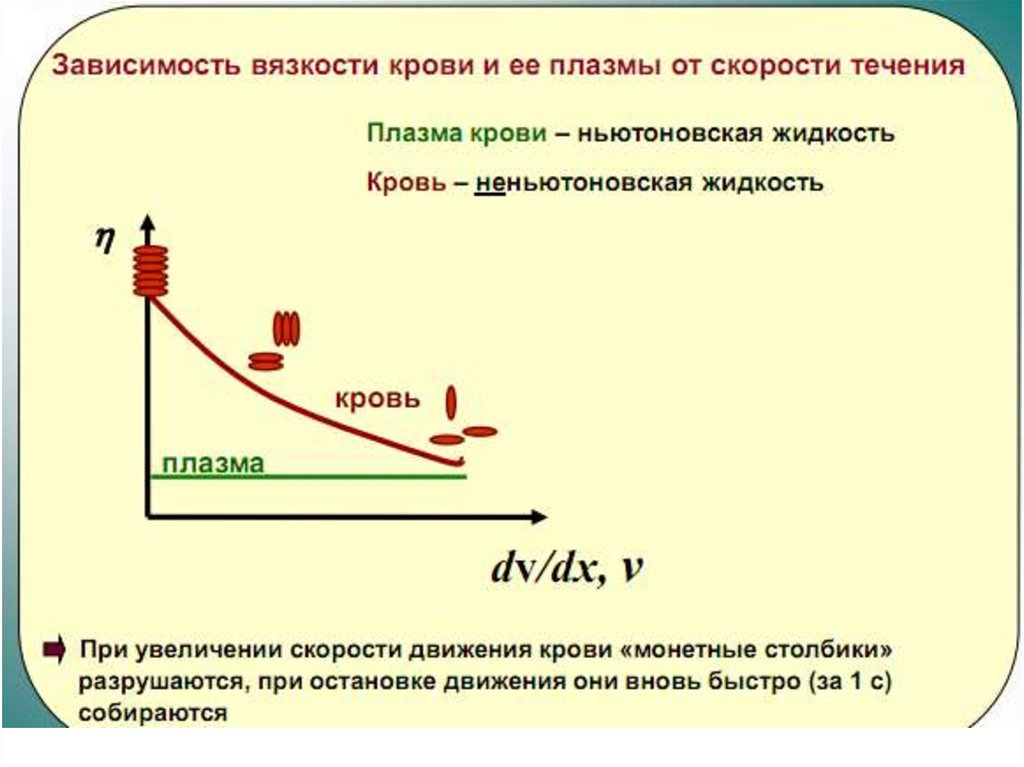
Различают ньютоновские и неньютоновские жидкости

13.

14.

15.

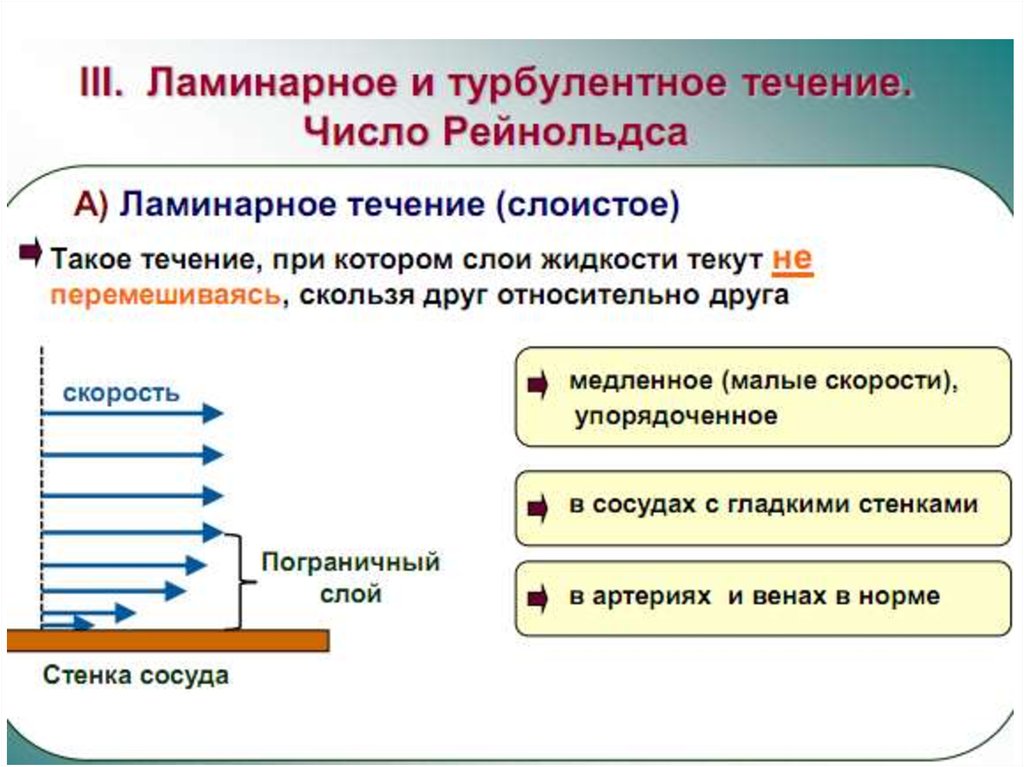
Существует два режима течения жидкостей:
ламинарный (слоистый) и турбулентный (вихревой).
Течение называется ламинарным, если вдоль потока каждый
выделенный тонкий слой скользит относительно соседних, не
перемешиваясь с ними.
max 2
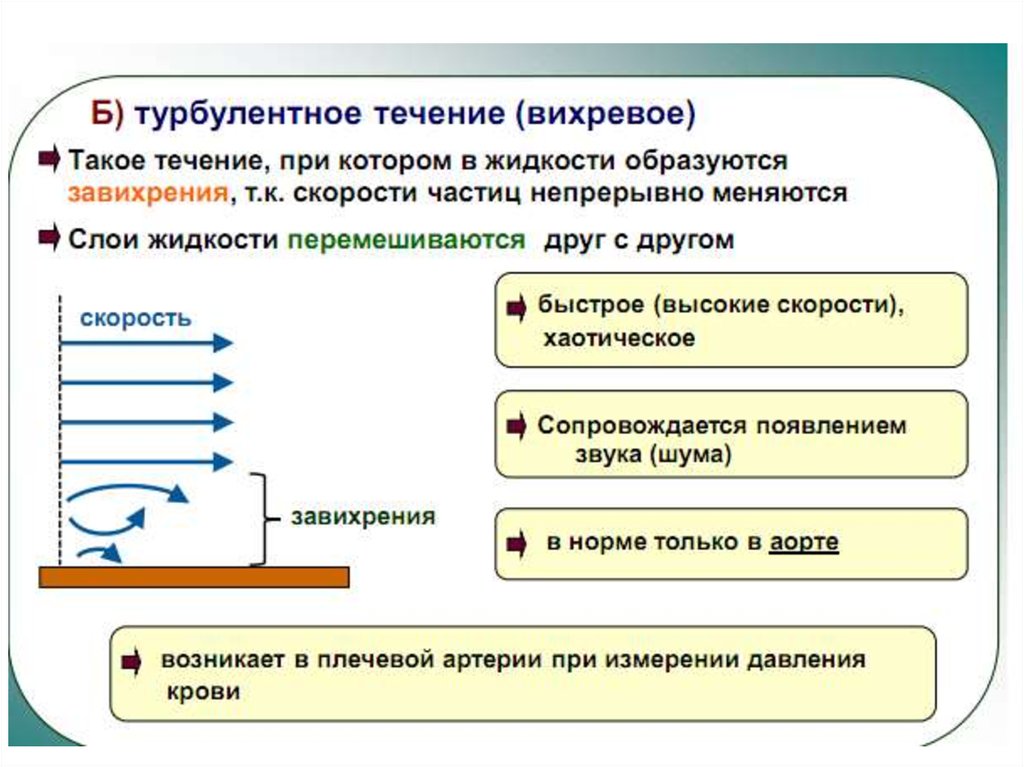
Течение называется турбулентным, если вдоль потока происходит
интенсивное вихреобразование и перемешивание жидкости (газа).
max 1, 23

16.

17.

18.

19.

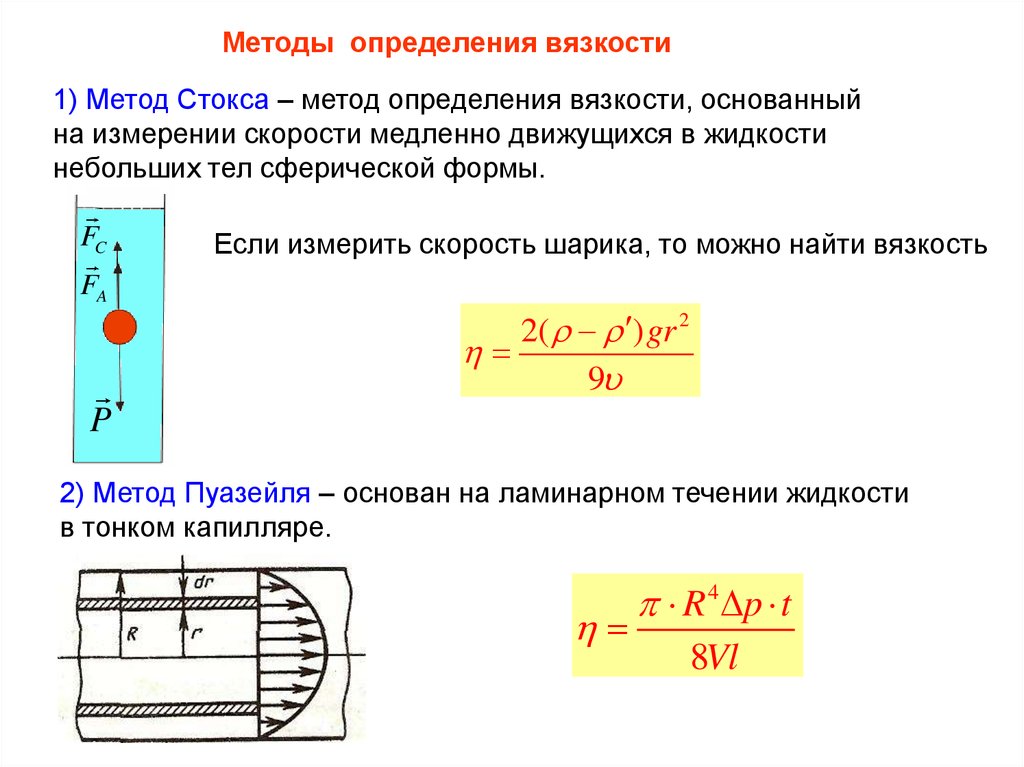
Методы определения вязкости
1) Метод Стокса – метод определения вязкости, основанный
на измерении скорости медленно движущихся в жидкости
небольших тел сферической формы.
FC
Если измерить скорость шарика, то можно найти вязкость
FA
2( ) gr 2
9
P
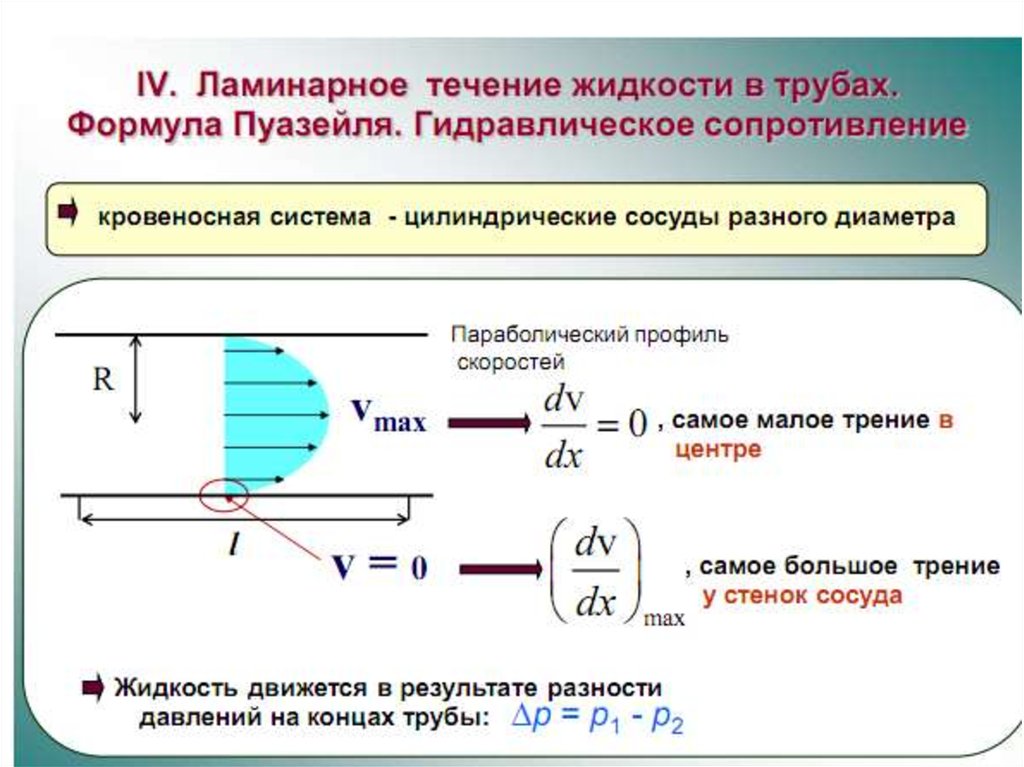
2) Метод Пуазейля – основан на ламинарном течении жидкости
в тонком капилляре.
R 4 p t
8Vl

20.

21.

3. Модель кровообращения Франка. Пульсовая волна. Формула
Моенса-Кортевега.
Модель кровообращения Франка позволяет установить связь между
ударным объемом крови (объем крови, выбрасываемый желудочком за одну
систолу), гидравлическим сопротивлением периферической части системы
кровообращения х0 и изменением давления в артериях.
Артериальная часть системы кровообращения моделируется упругим
(эластичным) резервуаром (УР).
В УР (артерия) поступает кровь из сердца со скоростью Q. От УР кровь
оттекает со скоростью Q0 в периферическую систему (артериолы,
капилляры).

22.

Объем крови в УР зависит от давления P
V=V0+kP,
(1)
где k - упругость резервуара;V0 - объем УР при P=0.
Возьмем первую производную
dV
dP
k
dt
dt
Q
dV
Q0
dt
(2)
(3)
т.е. объемная скорость кровотока из сердца равна скорости возрастания
объема УР, т.е. скорости оттока крови из упругого резервуара.

23.

На основании формулы Пуазейля и формулы (3) можно записать для
периферии:
P Pв
Q0
x0
(4)
где P - давление в УР; Pв - венозное давление. При Pв = 0
Q0
P
x0
(5)
Подставляя (2) и (5) в (3), получим
Q k
dP P
dt x0
или Qdt kdP
P
dt
x0
(6)

24.

Во время систолы (сокращение сердца) происходит расширение УР, во время
диастолы - отток крови к периферии, Q=0. Тогда (6) перепишется:
0 kdP
P
dt или
x0
dP
dt
P
kx0
(7)
Проинтегрировав (9), получаем зависимость давления в УР после
систолы от времени:
P Pc
t
kx0
и Q Qc
t
kx0
(8)

25.

Пульсовая волна - это распространяющаяся по аорте и артериям волна
повышенного давления, вызванная выбросом крови из левого желудочка в
период систолы.
Скорость пульсовой волны в крупных сосудах определяется формулой
Моенса-Кортевега:
Eh
d
где Е - модуль упругости, - плотность вещества сосуда, h - толщина
стенки сосуда, d-диаметр сосуда.