Похожие презентации:
ТПР . Многопараметрические методы оптимизации. (Занятие 5)
1.
ОСНОВЫ ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙЗанятие 5
2
Итак, мы с Вами приступили к изучению многопараметрических методов оптимизации, рассмотрели
аналитический метод в многомерном пространстве
(правда, довольно поверхностно) и договорились о
том, каким графическим приёмом мы будем пользоваться для иллюстрации методов, следующих далее.
Двинемся дальше, вернее ниже, если обратиться
к показанному слева фрагменту классификации.
Метод Гаусса-Зайделя
Карл Фридрих Гаусс (1777-1855)
Немецкий математик, механик, физик,
астроном и геодезист. Считается одним
из величайших математиков всех
времён, «королём математиков».
Филипп Людвиг фон Зайдель (1821 – 1896)
Немецкий математик. Его именем назван
один из лунных кратеров.
2.
2Основные принципы метода Гаусса-Зайделя
Предлагается двигаться к оптимуму, выполняя серии дискретных опытов.
В каждой серии следует с заданным шагом изменять только один из факторов,
а остальные факторы сохранять неизменными.
Серию надо продолжать до тех пор, пока движение приводит к улучшению
критерия оптимизации
Если критерий оптимизации начал ухудшаться, серию надо остановить,
выбрать тот из опытов, который дал наилучший результат, и использовать
его координаты для планирования новой серии, в которой изменяться
будет уже другой фактор.
Если изменение любого из факторов приводит к ухудшению результата,
можно принять одно из двух решений:
• успокоиться на этом и считать оптимальными координаты того опыта,
который дал наилучшее значение критерия;
• если ресурсы не исчерпаны и Заказчик требует дальнейшего улучшения,
можно продолжить поиск в окрестности найденного экстремума,
уменьшив шаги движения.
3.
2X2
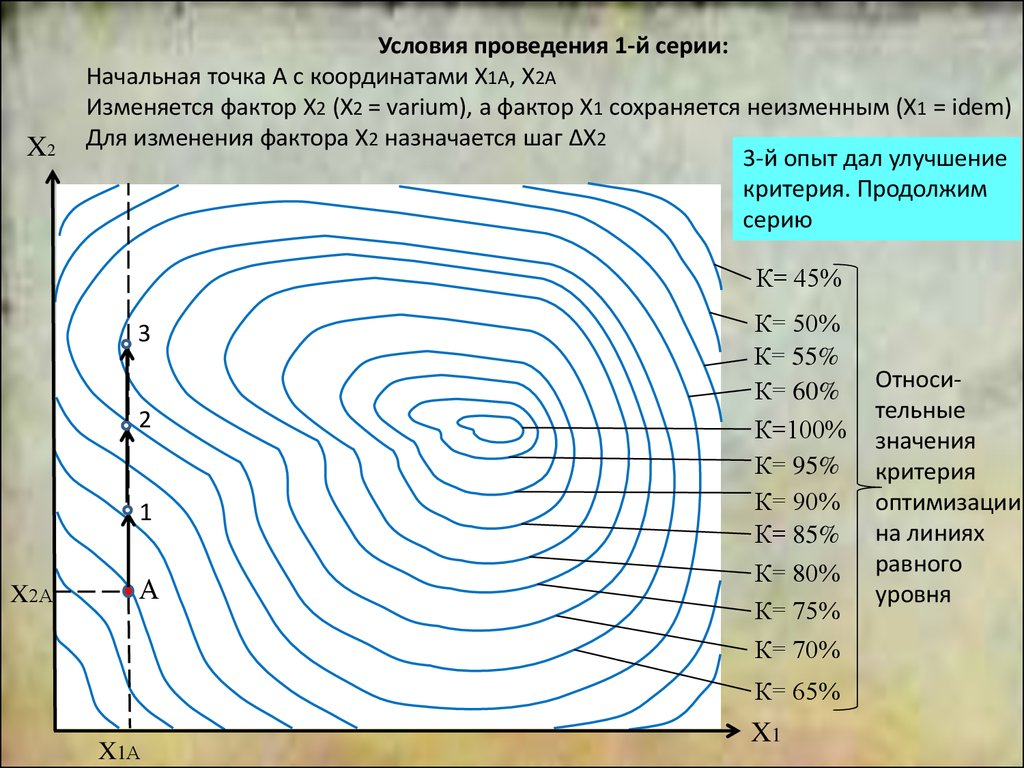
Условия проведения 1-й серии:
Начальная точка А с координатами Х1А, Х2А
Изменяется фактор Х2 (Х2 = varium), а фактор Х1 сохраняется неизменным (Х1 = idem)
Для изменения фактора Х2 назначается шаг ΔХ2
1-й опыт дал улучшение
критерия. Продолжим
серию
К= 45%
К= 8
К= 7
К= 6
К= 5
К= 4
1
X2А
А
К= 3
К= 2
К= 1
К= 50%
К= 55%
К= 60%
К=100%
К= 95%
К= 90%
К= 85%
К= 80%
К= 75%
К= 70%
К= 65%
X1А
X1
Относительные
значения
критерия
оптимизации
на линиях
равного
уровня
4.
2X2
Условия проведения 1-й серии:
Начальная точка А с координатами Х1А, Х2А
Изменяется фактор Х2 (Х2 = varium), а фактор Х1 сохраняется неизменным (Х1 = idem)
Для изменения фактора Х2 назначается шаг ΔХ2
2-й опыт дал улучшение
критерия. Продолжим
серию
К= 45%
К= 8
К= 7
К= 6
2
К= 5
К= 4
1
X2А
А
К= 3
К= 2
К= 1
К= 50%
К= 55%
К= 60%
К=100%
К= 95%
К= 90%
К= 85%
К= 80%
К= 75%
К= 70%
К= 65%
X1А
X1
Относительные
значения
критерия
оптимизации
на линиях
равного
уровня
5.
2X2
Условия проведения 1-й серии:
Начальная точка А с координатами Х1А, Х2А
Изменяется фактор Х2 (Х2 = varium), а фактор Х1 сохраняется неизменным (Х1 = idem)
Для изменения фактора Х2 назначается шаг ΔХ2
3-й опыт дал улучшение
критерия. Продолжим
серию
К= 45%
3
2
К= 8
К= 7
К= 6
К= 5
К= 4
1
X2А
А
К= 3
К= 2
К= 1
К= 50%
К= 55%
К= 60%
К=100%
К= 95%
К= 90%
К= 85%
К= 80%
К= 75%
К= 70%
К= 65%
X1А
X1
Относительные
значения
критерия
оптимизации
на линиях
равного
уровня
6.
2X2
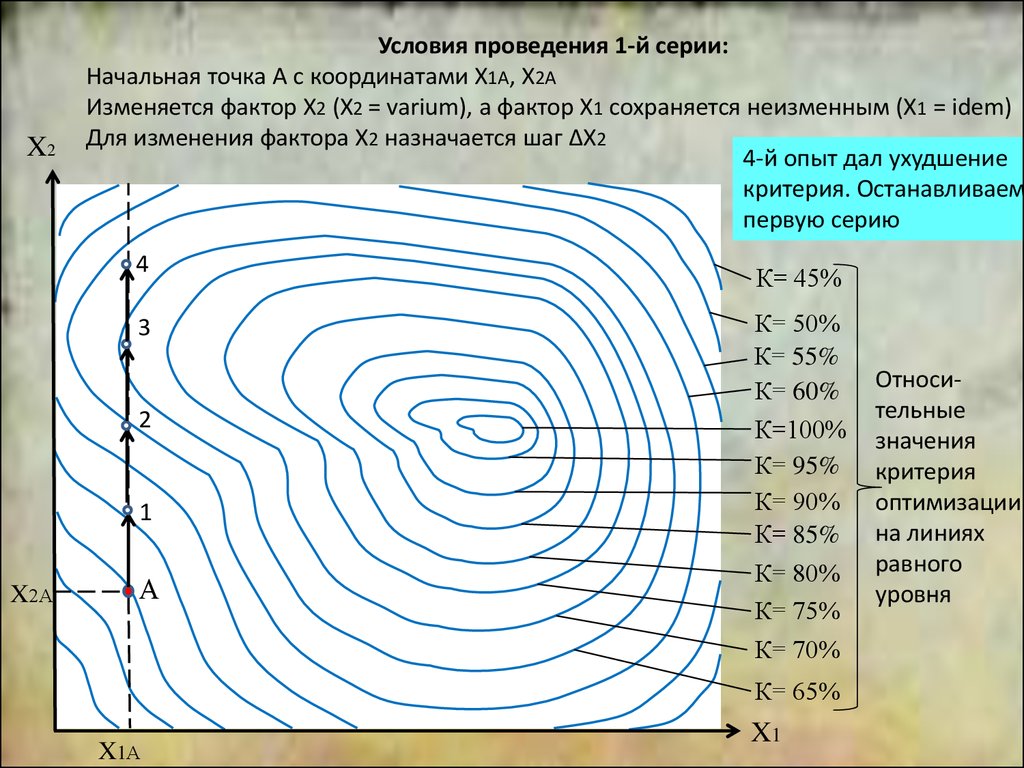
Условия проведения 1-й серии:
Начальная точка А с координатами Х1А, Х2А
Изменяется фактор Х2 (Х2 = varium), а фактор Х1 сохраняется неизменным (Х1 = idem)
Для изменения фактора Х2 назначается шаг ΔХ2
4-й опыт дал ухудшение
критерия. Останавливаем
первую серию
4
3
2
К= 45%
К= 8
К= 7
К= 6
К= 5
К= 4
1
X2А
А
К= 3
К= 2
К= 1
К= 50%
К= 55%
К= 60%
К=100%
К= 95%
К= 90%
К= 85%
К= 80%
К= 75%
К= 70%
К= 65%
X1А
X1
Относительные
значения
критерия
оптимизации
на линиях
равного
уровня
7.
2Условия проведения 2-й серии:
X2
Начальная точка 3
Изменяется фактор Х1 (Х1 = varium), а фактор Х2 сохраняется неизменным (Х2 = idem)
Для изменения фактора Х1 назначается шаг ΔХ1
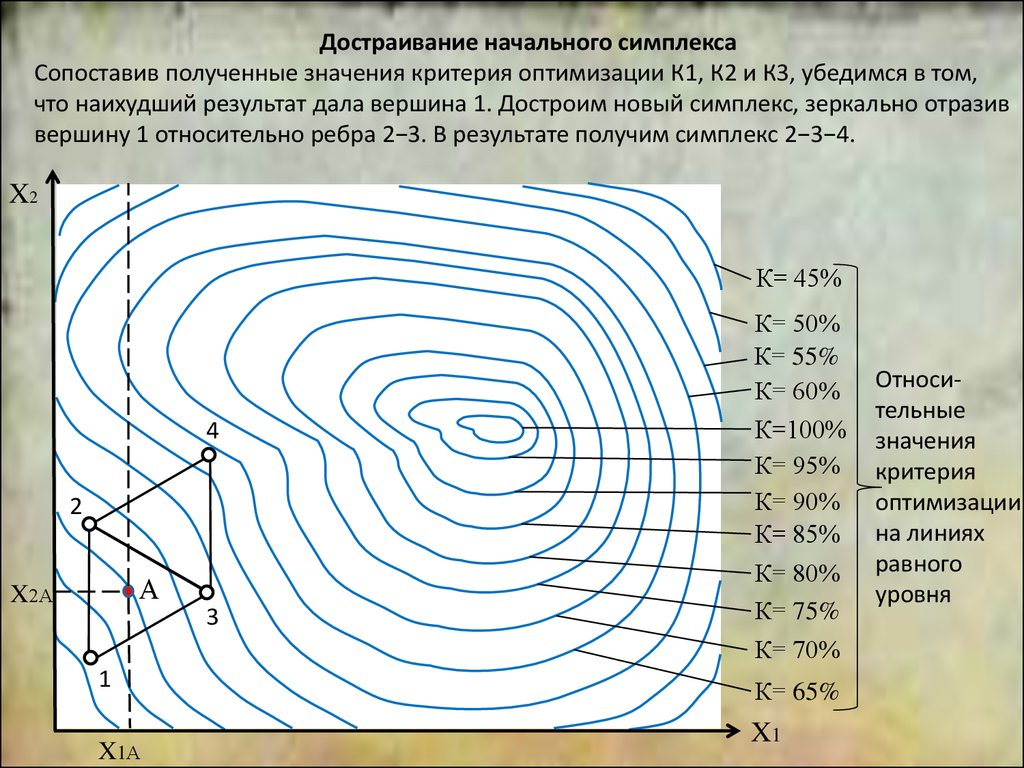
Опыты с 5 по 8 дали
улучшение критерия, а
9-й его ухудшил.
Планируем третью серию
4
3
2
К= 45%
5
6
7
К=
8 8
9
К= 7
К= 6
К= 5
К= 4
1
X2А
А
К= 3
К= 2
К= 1
К= 50%
К= 55%
К= 60%
К=100%
К= 95%
К= 90%
К= 85%
К= 80%
К= 75%
К= 70%
К= 65%
X1А
X1
Относительные
значения
критерия
оптимизации
на линиях
равного
уровня
8.
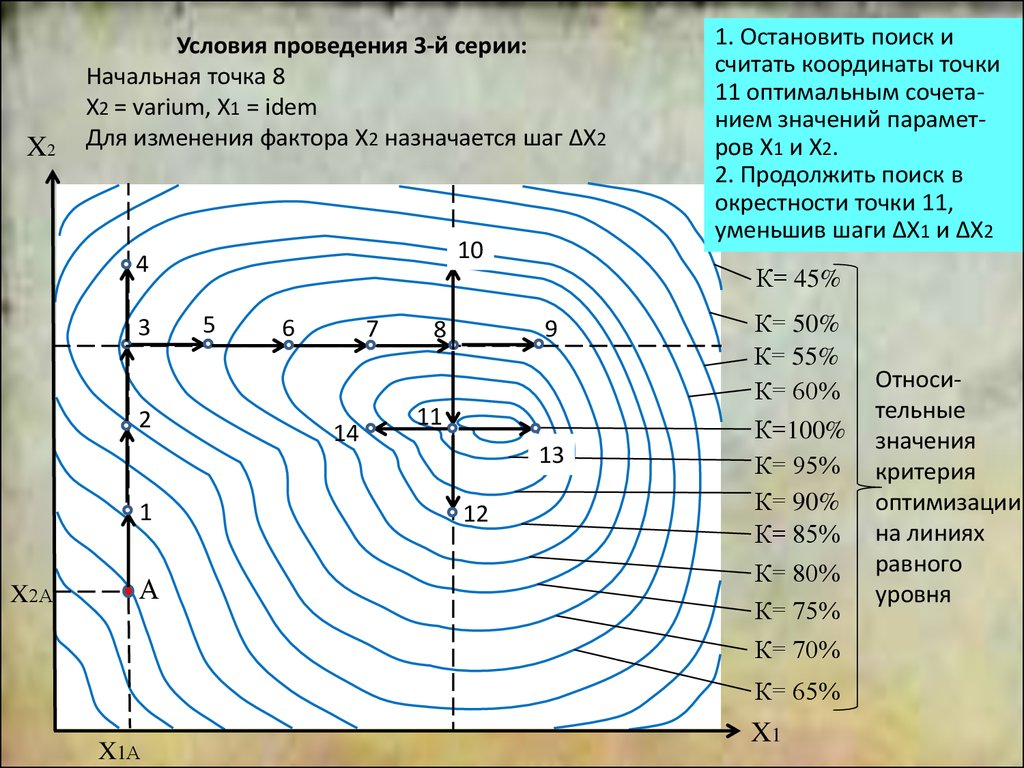
X2Условия проведения 3-й серии:
Начальная точка 8
Х2 = varium, Х1 = idem
Для изменения фактора Х2 назначается шаг ΔХ2
10
4
3
2
5
6
7
К= 45%
К=
9
8 8
К= 7
К= 6
К= 5
К= 4
1
X2А
А
2
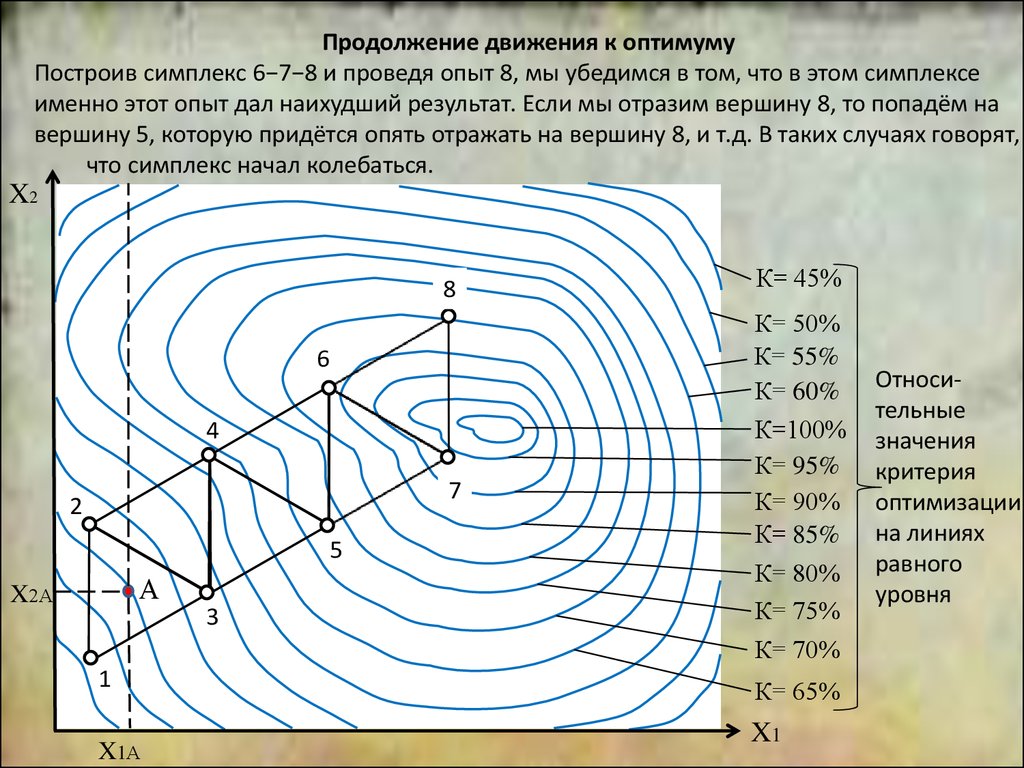
А вот куда двигаться:
вверх или вниз? Форма
«горы» нам априори не
известна, поэтому выбираем наугад. Допустим,
решили двигаться вверх.
Увы, опыт 10 ухудшил
результат.
К= 3
К= 2
К= 1
К= 50%
К= 55%
К= 60%
К=100%
К= 95%
К= 90%
К= 85%
К= 80%
К= 75%
К= 70%
К= 65%
X1А
X1
Относительные
значения
критерия
оптимизации
на линиях
равного
уровня
9.
X2Условия проведения 3-й серии:
Начальная точка 8
Х2 = varium, Х1 = idem
Для изменения фактора Х2 назначается шаг ΔХ2
10
4
3
2
5
6
7
X2А
А
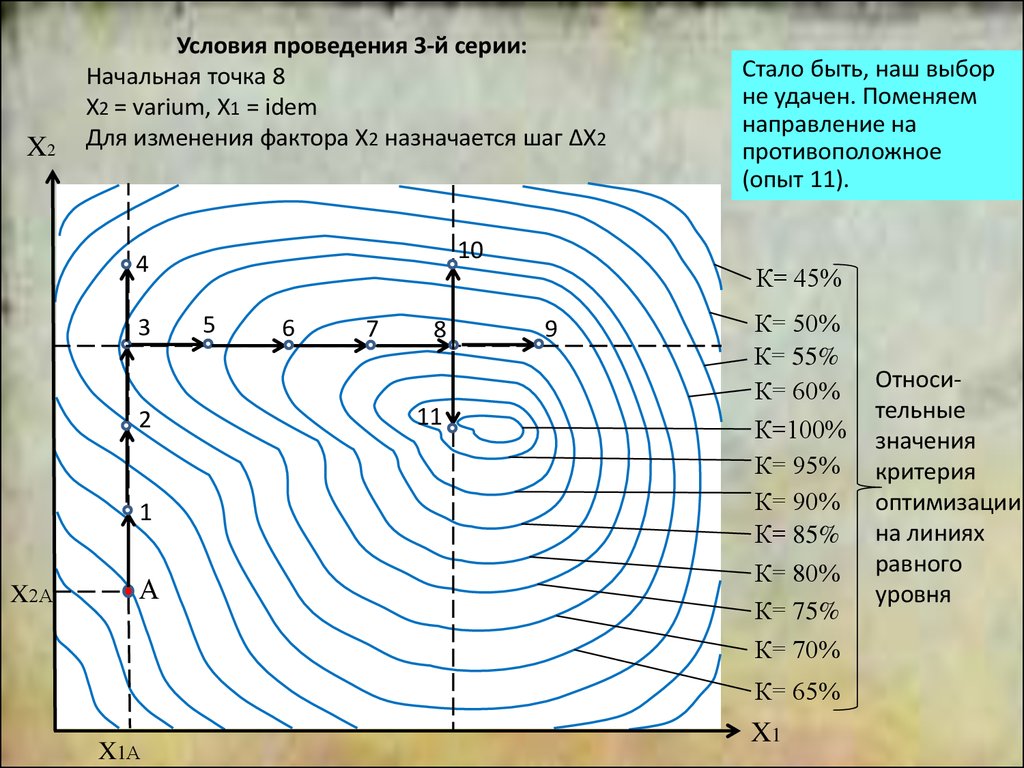
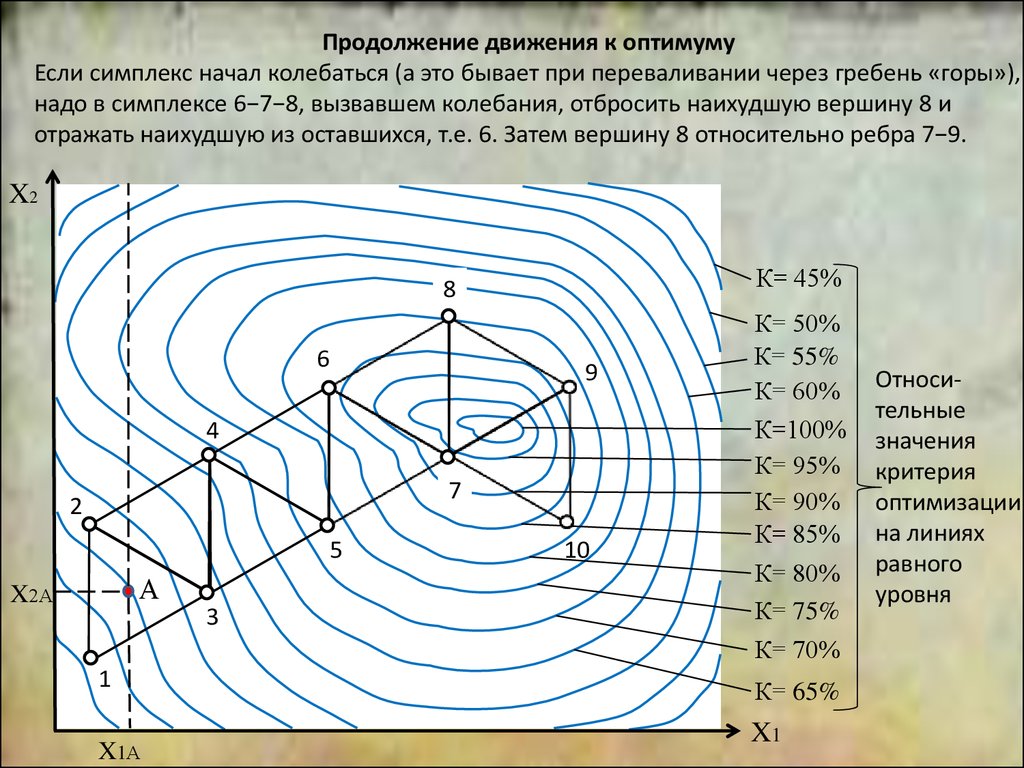
Стало быть, наш выбор
не удачен. Поменяем
направление на
противоположное
(опыт 11).
К= 45%
К=
9
8 8
К= 7
К= 6
11
К= 5
К= 4
1
2
К= 3
К= 2
К= 1
К= 50%
К= 55%
К= 60%
К=100%
К= 95%
К= 90%
К= 85%
К= 80%
К= 75%
К= 70%
К= 65%
X1А
X1
Относительные
значения
критерия
оптимизации
на линиях
равного
уровня
10.
X2Условия проведения 3-й серии:
Начальная точка 8
Х2 = varium, Х1 = idem
Для изменения фактора Х2 назначается шаг ΔХ2
10
4
3
2
1
X2А
А
5
6
7
14
2
Продолжая действовать
в том же духе, убедимся
в том, что движение в
любую сторону от точки
11 приводит к ухудшению критерия. Тут надо
принимать одно из двух
решений:
К= 45%
К=
9
8 8
К= 7
К= 6
11
К= 5
13
К= 4
12
К= 3
К= 50%
К= 55%
К= 60%
К= 2
К= 80%
К= 75%
К= 1
К=100%
К= 95%
К= 90%
К= 85%
К= 70%
К= 65%
X1А
X1
Относительные
значения
критерия
оптимизации
на линиях
равного
уровня
11.
X2Условия проведения 3-й серии:
Начальная точка 8
Х2 = varium, Х1 = idem
Для изменения фактора Х2 назначается шаг ΔХ2
10
4
3
2
1
X2А
А
5
6
7
14
1. Остановить поиск и 2
считать координаты точки
11 оптимальным сочетанием значений параметров Х1 и Х2.
2. Продолжить поиск в
окрестности точки 11,
уменьшив шаги ΔХ1 и ΔХ2
К= 45%
К=
9
8 8
К= 7
К= 6
11
К= 5
13
К= 4
12
К= 3
К= 50%
К= 55%
К= 60%
К= 2
К= 80%
К= 75%
К= 1
К=100%
К= 95%
К= 90%
К= 85%
К= 70%
К= 65%
X1А
X1
Относительные
значения
критерия
оптимизации
на линиях
равного
уровня
12.
2Достоинства метода Гаусса-Зайделя
Метод обеспечивает последовательное улучшение результата. Поэтому, даже если
обстоятельства не позволили целиком пройти весь путь к оптимуму, Вы всё-же частично
улучшите исходное состояние объекта (если, конечно, это в принципе возможно).
Метод адаптивен к свойствам объекта, т.е. он обеспечивает автоматический разворот
направления поиска в сторону оптимального решения.
Метод устойчив, т.е. неправильный выбор направления движения временно ухудшает
ситуацию, но затем алгоритм поиска обеспечивает автоматическую корректировку
траектории движения.
Метод, в принципе, способен обеспечить сколь угодно точное нахождение оптимума
путём соответствующего выбора шагов изменения факторов (разумеется, если Вы
располагаете неограниченным запасом ресурсов, времени и терпения).
Недостатки метода Гаусса-Зайделя
Слишком длинный путь к оптимуму, особенно, при большом количестве факторов.
Если это чисто математический малозатратный поиск, то это не так критично, но если
определение значений критерия при каждой заданной комбинации значений
факторов требует проведения реальных экспериментов и испытаний, медленный путь
к оптимуму обернётся большими затратами времени и ресурсов.
Если в зоне поиска имеется несколько экстремумов, то метод не гарантирует выход
на самый благоприятный из них.
13.
2В чём причина медлительности метода Гаусса-Зайделя?
Представьте себе альпинистов, идущих к вершине горы по кусочно-линейной траектории,
содержащей только широтные (запад-восток) и меридиональные (север-юг) участки.
Наверное, они очень нескоро водрузят победный флаг на вершине.
Нельзя ли как-то сократить этот путь?
Понятно, что кратчайшей траекторией была бы прямая, соединяющая отправную точку
с вершиной. Но реальным альпинистам так двигаться не позволяет сложная форма
склонов. Да и вершина горы людям, стоящим у её подножья, обычно не видна.
Тем не менее, можно форсировать восхождение, если осмотреться вокруг
и начать движение в направлении наиболее крутого склона.
Нам с Вами форма склонов нашей математической горы помешать не может, а вот
второе препятствие значимо и для нас: мы тоже не видим вершину.
Ну что же, давайте поступим аналогичным образом: изучим свойства нашего объекта в
окрестности отправной точки и будем двигаться в том направлении, в котором функция
K = f(X1, X2) изменяется с максимальной скоростью.
Вектор, указывающий направление наибольшей интенсивности изменения функции,
математики называют градиентом. Значит, и придуманный нами метод, можно назвать
градиентным.
Справедливости ради надо указать, что его ещё раньше – в 1951 году – предложили
Box и Wilson. С тех пор его так и называют: метод Бокса-Уилсона. А также метод «крутого
восхождения» (если нужен максимум критерия) или «наискорейшего спуска» (если
нужен минимум).
14.
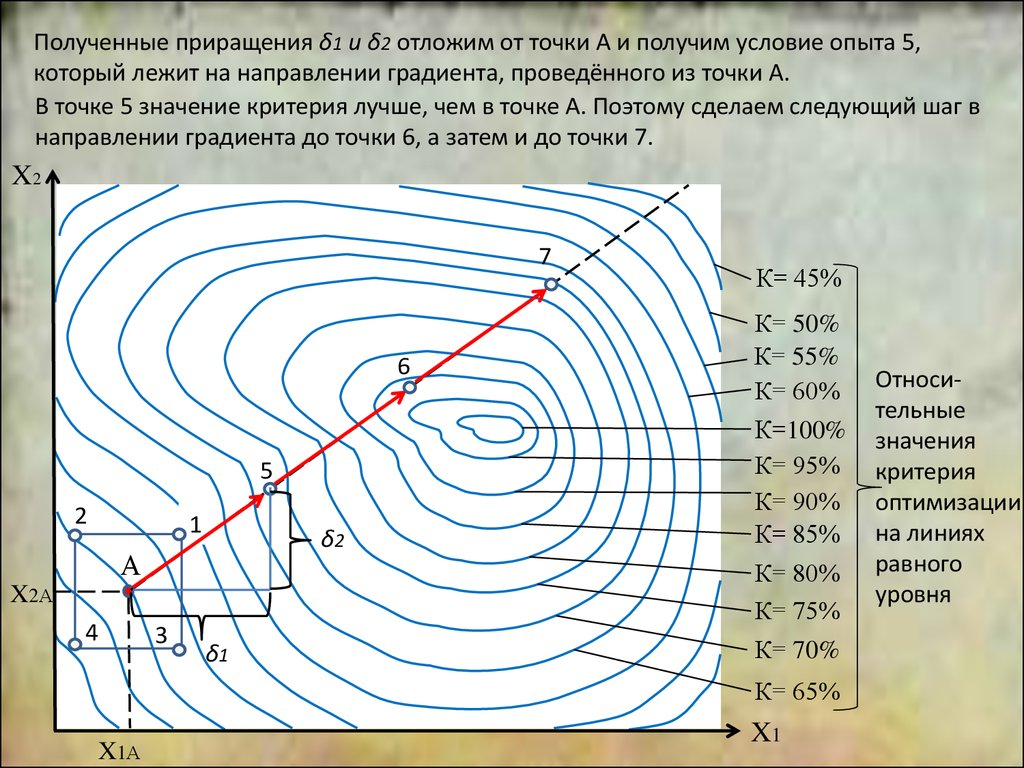
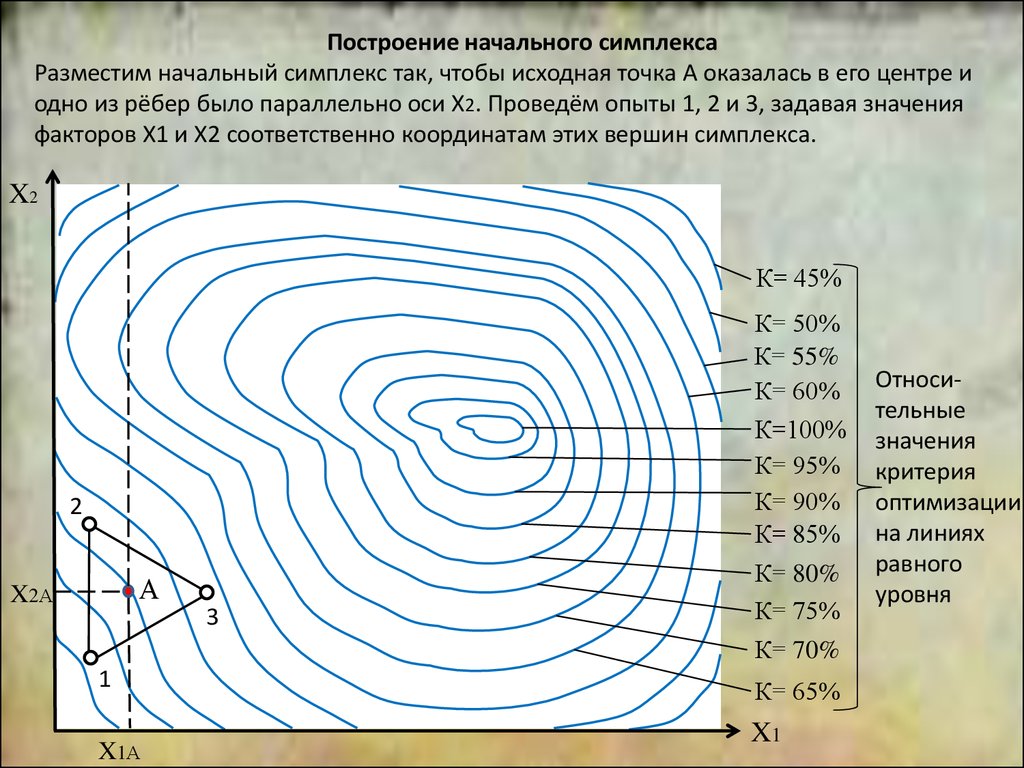
Для изучения свойств объекта в окрестности точки Апроведём начальную серию опытов в соответствие
с планом полного факторного эксперимента на двух
уровнях (опыты 1÷4).
Полученная матрица:
X2
2
Опыты
Х1
Х2
К
1
+
+
К1
2
-
+
К2
3
+
-
К3
4
-
-
К4
К= 45%
К= 8
К= 7
К= 6
К= 5
К= 4
2
1
К= 2
А
X2А
К= 1
4
3
X1А
К= 3
К= 50%
К= 55%
К= 60%
К=100%
К= 95%
К= 90%
К= 85%
К= 80%
К= 75%
К= 70%
К= 65%
X1
Относительные
значения
критерия
оптимизации
на линиях
равного
уровня
15.
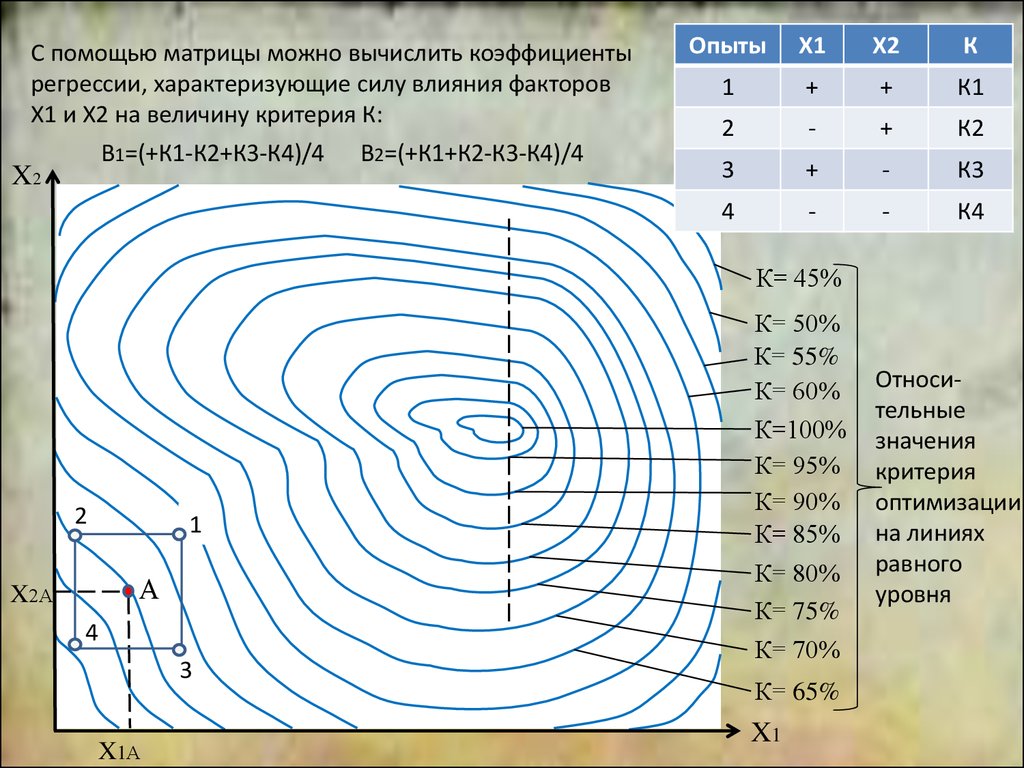
С помощью матрицы можно вычислить коэффициентырегрессии, характеризующие силу влияния факторов
Х1 и Х2 на величину критерия К:
В1=(+К1-К2+К3-К4)/4
X2
В2=(+К1+К2-К3-К4)/4
2
Опыты
Х1
Х2
К
1
+
+
К1
2
-
+
К2
3
+
-
К3
4
-
-
К4
К= 45%
К= 8
К= 7
К= 6
К= 5
К= 4
2
1
К= 2
А
X2А
К= 1
4
3
X1А
К= 3
К= 50%
К= 55%
К= 60%
К=100%
К= 95%
К= 90%
К= 85%
К= 80%
К= 75%
К= 70%
К= 65%
X1
Относительные
значения
критерия
оптимизации
на линиях
равного
уровня
16.
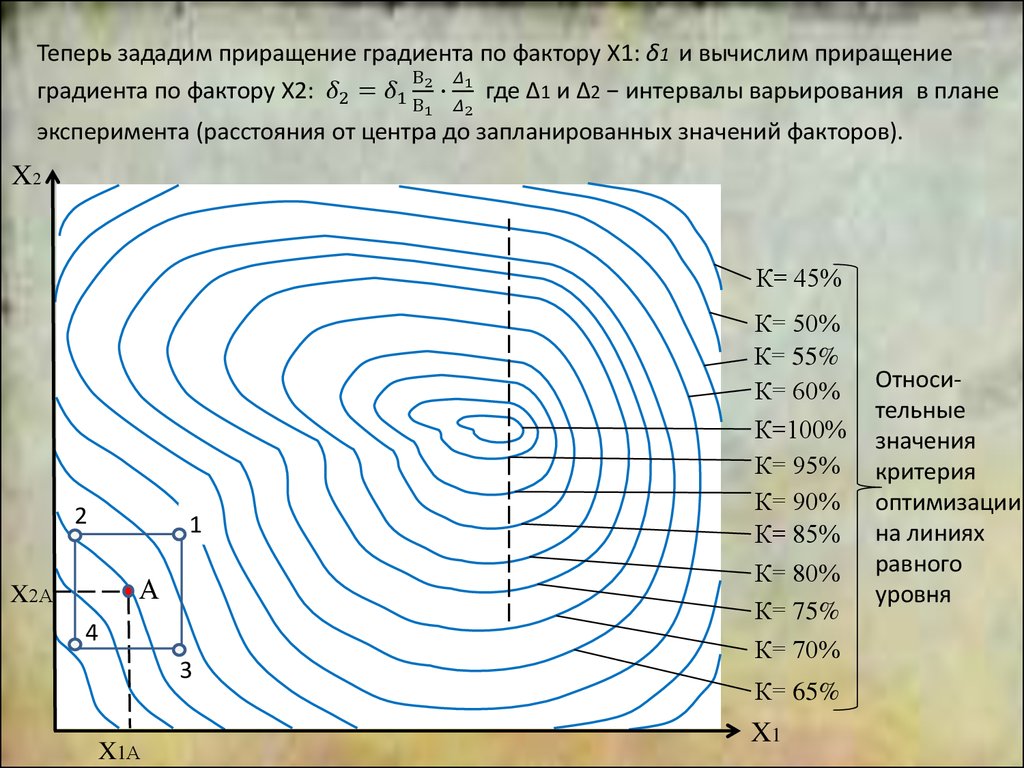
2Теперь зададим приращение градиента по фактору Х1: δ1 и вычислим приращение
В
















 Менеджмент
Менеджмент